
In geometry, certain shapes exhibit unique characteristics that define their structure and behavior. These shapes can be classified based on their sides, angles, and symmetry. Among these, a specific category of quadrilaterals has distinct features that are crucial for solving geometric problems and understanding spatial relationships.
Recognizing these traits is essential when tackling questions related to angles, sides, and other measurements within these figures. By learning how to identify and apply these properties, students and enthusiasts can improve their problem-solving skills and deepen their understanding of geometric principles.
In this guide, we will explore the fundamental attributes of these four-sided shapes, focusing on their defining aspects and how to work with them in mathematical exercises. Whether you’re solving for area, perimeter, or exploring their geometric behavior, mastering these key concepts will enhance your overall grasp of the subject.
Properties of Parallelograms Answer Key
When working with four-sided shapes, it’s important to understand the fundamental characteristics that govern their behavior. These shapes share common traits that help solve various problems involving angles, sides, and symmetry. In this section, we will highlight key facts and guidelines for identifying and working with these geometric figures.
Below are the essential attributes that define these quadrilaterals:
- Opposite sides are equal in length: This is a key feature that helps distinguish this type of shape from other quadrilaterals.
- Opposite angles are congruent: The angles across from each other are always the same measure.
- Consecutive angles are supplementary: The sum of any two adjacent angles equals 180°.
- Diagonals bisect each other: The diagonals cut each other exactly in half, creating two equal parts.
- Parallel sides: Opposite sides are parallel to one another, a critical aspect for solving problems related to parallelism and angle measurement.
These attributes form the foundation for solving related problems, such as finding the area, perimeter, or angles of such shapes. Understanding these basic properties will help you approach more complex geometric problems with confidence.
For practical application, let’s review how to use these characteristics in different types of exercises:
- Problem 1: Area Calculation – Use the formula base × height to find the area when given the necessary dimensions.
- Problem 2: Perimeter Calculation – The perimeter is simply the sum of all the sides, or 2 × (length + width) if the shape is a rectangle.
- Problem 3: Angle Sum – Knowing that consecutive angles add up to 180°, you can easily calculate missing angle measures.
- Problem 4: Diagonal Length – Use the properties of the diagonals to determine their relationship with side lengths, particularly in cases where they bisect each other.
By mastering these core principles, you can confidently tackle various geometry problems and better understand the behavior of these shapes in both theoretical and real-world applications.
Understanding Parallelograms in Geometry
In the study of shapes and their properties, certain four-sided figures play a crucial role in understanding fundamental geometric principles. These figures have distinct characteristics that make them unique among other quadrilaterals. By recognizing these key features, one can gain a deeper understanding of how to solve problems involving angles, sides, and other related measurements.
Key Features of Four-Sided Shapes

These specific shapes share several important traits. For example, their opposite sides are always of equal length, and their angles exhibit specific relationships. The symmetry within these figures further enhances their utility in geometry, making them easier to analyze when solving mathematical problems.
Importance in Geometry
Understanding the behavior of these figures is not just about memorizing their features; it’s about applying this knowledge to real-world problems. Whether you’re calculating area, finding missing angles, or exploring spatial relationships, these shapes provide a foundation for many geometric concepts.
By grasping their basic attributes, students and enthusiasts can approach geometry problems with confidence and clarity. These shapes are often encountered in both academic exercises and practical scenarios, making them essential in the study of geometry.
Key Characteristics of Parallelograms
In geometry, certain four-sided shapes exhibit distinct features that help define their structure and behavior. These traits are fundamental for solving problems involving measurements such as side lengths, angles, and area. Understanding these characteristics is essential for tackling both simple and complex geometric tasks.
Some of the most important aspects of these shapes include the equality of opposite sides, the congruence of opposite angles, and the parallelism of opposite sides. Additionally, the diagonals of these shapes hold specific relationships to each other, providing further insight into their geometric properties.
By mastering these characteristics, you can confidently approach exercises and real-life applications where these figures are involved, from calculating area and perimeter to analyzing symmetry and spatial relationships.
Angles and Sides of Parallelograms
Understanding the relationship between the angles and sides of these four-sided figures is essential for solving geometric problems. These shapes exhibit specific patterns in their angles and side lengths, which are crucial when working with calculations or proving geometric theorems. By recognizing these patterns, one can easily identify missing values or solve for unknown measurements.
The opposite sides of these shapes are always equal in length, while the consecutive angles are supplementary, meaning they add up to 180°. In addition, the opposite angles are congruent, making it possible to determine the value of one angle if another is known.
| Side Relationship | Angle Relationship |
|---|---|
| Opposite sides are equal in length | Opposite angles are congruent |
| Adjacent sides are not necessarily equal | Consecutive angles are supplementary (sum to 180°) |
These relationships form the basis for many problems involving these figures, helping to simplify complex geometric tasks such as finding the area or solving for unknown angle measures.
Diagonals and Their Properties
In geometry, the diagonals of a quadrilateral play an important role in understanding the overall structure and relationships within the figure. These line segments, which connect opposite corners, provide valuable insights into the symmetry, angles, and area calculations of the shape. Understanding their behavior is crucial when solving geometric problems involving such figures.
Key Characteristics of Diagonals

For these types of figures, one of the most important properties is that the diagonals bisect each other. This means that the diagonals intersect at their midpoints, dividing each diagonal into two equal parts. This characteristic can be used to simplify calculations or prove certain geometric theorems.
Applications in Geometry
Diagonals also offer a way to determine other key aspects of the shape, such as the area. In some cases, the diagonals create triangles within the figure, which can be analyzed using familiar geometric formulas. By using the relationship between the diagonals and the sides, you can find missing values or confirm the properties of the shape.
Area Formula for Parallelograms
Calculating the area of certain quadrilaterals involves understanding the relationship between their base and height. The area measurement is essential for various practical applications, from architectural design to simple geometric problem-solving. In these shapes, the area is determined by multiplying the length of one side by the perpendicular distance between the opposite sides.
The formula for calculating the area of these figures is straightforward:
Area = Base × Height
Here, the base refers to any one of the sides, while the height is the perpendicular distance from the chosen base to the opposite side. It’s important to ensure that the height is measured at a right angle to the base, as this ensures an accurate calculation.
This method of calculating area applies regardless of the angles or side lengths, as long as the shape has the required properties. Mastering this formula allows for efficient problem-solving in geometry and can be applied in real-world contexts where space and area need to be measured.
Perimeter Calculation for Parallelograms
To determine the perimeter of these four-sided figures, one must understand how the sides contribute to the total length around the figure. Unlike calculating area, where you consider the height, perimeter involves simply adding up the lengths of all the sides. In these shapes, the opposite sides are always equal, making the calculation simpler.
The formula for finding the perimeter is as follows:
Perimeter = 2 × (Length + Width)
Here, the length and width refer to the dimensions of the sides. Since the opposite sides are equal, you only need to measure two different side lengths to calculate the perimeter. Below is a step-by-step breakdown of how to perform this calculation:
- Measure the length of one pair of opposite sides.
- Measure the length of the other pair of opposite sides.
- Add these two values together.
- Multiply the result by 2 to account for both pairs of sides.
For example, if one pair of sides measures 5 units and the other pair measures 3 units, the perimeter is:
Perimeter = 2 × (5 + 3) = 2 × 8 = 16 units
This simple approach makes it easy to calculate the perimeter for any such figure, ensuring accuracy in various geometric tasks and real-world applications like land measurement or construction planning.
How to Prove a Shape is a Parallelogram

In geometry, demonstrating that a four-sided figure meets certain criteria is a key step in classifying it. Proving that a figure belongs to a specific category requires verifying that it possesses specific characteristics or relationships between its sides, angles, and diagonals. There are several methods that can be used to prove that a shape has the necessary features to be classified in this way.
Methods of Proof
Here are the most common approaches used to prove a shape fits the criteria:
- Opposite sides are parallel: If both pairs of opposite sides are parallel, then the figure must meet the criteria.
- Opposite sides are equal: Another way to prove the shape is to show that both pairs of opposite sides are equal in length.
- Opposite angles are congruent: If opposite angles are equal, this can be used as evidence that the figure is the desired shape.
- Diagonals bisect each other: If the diagonals of the shape intersect at their midpoints, this is a clear indication that the figure possesses the necessary characteristics.
Step-by-Step Proof

To formally prove that a shape is of the desired type, follow these steps:
- Identify the known properties of the figure, such as side lengths and angle measures.
- Apply one or more of the methods listed above to verify the necessary relationships.
- If the required conditions are met, conclude that the shape is classified as the desired type.
By carefully analyzing these properties, it is possible to definitively prove whether a figure meets the criteria, making it easier to work with and apply geometric formulas for calculations like area or perimeter.
Types of Parallelograms and Their Differences
In the realm of geometry, four-sided figures with opposite sides parallel can vary significantly in their specific characteristics and appearance. While they share certain common traits, subtle differences in angles and side lengths distinguish them from one another. Understanding these distinctions helps in identifying and working with these shapes in various mathematical and practical contexts.
There are several types of these four-sided figures, each with its own unique properties. Here are the most common types and their key differences:
- Rectangle: All angles are right angles (90°), and opposite sides are equal in length. A rectangle can be considered a specific type of figure with additional constraints.
- Rhombus: All sides are of equal length, and opposite angles are congruent. However, the angles are not necessarily 90°, which makes it different from a square.
- Square: A special case of both a rectangle and a rhombus, where all sides are equal, and all angles are right angles (90°).
- Rhomboid: Opposite sides are equal in length and parallel, but the angles are not necessarily right angles. It is a more generalized form than a rectangle or rhombus.
Each of these types shares the fundamental property of having opposite sides that are parallel, but their internal angles and side relationships can vary. Recognizing these differences allows for a more nuanced understanding of geometry and can help when solving specific types of problems or performing calculations.
Applications of Parallelograms in Real Life
The unique characteristics of these four-sided figures with opposite sides parallel make them highly useful in many practical situations. From architecture to engineering, these shapes provide a foundation for understanding structural stability, design efficiency, and various forms of artwork. Their properties help solve real-world problems, ensuring that objects are both functional and aesthetically pleasing.
One of the most prominent areas where these figures are applied is in construction. Beams, supports, and certain architectural elements often rely on these shapes to distribute weight evenly. Additionally, in engineering, the concept of tension and compression in structures such as bridges or towers involves principles that can be described using these figures.
Some common real-life applications include:
- Construction and Architecture: The design of roofs, walls, and even floor plans often incorporates these shapes, ensuring that structures are stable and strong.
- Furniture Design: Many pieces of furniture, such as tables, chairs, and shelving units, use this shape for stability and aesthetic balance.
- Art and Design: These shapes appear frequently in graphic design, pattern creation, and artwork, allowing for symmetry and geometric beauty.
- Navigation: Geometrical models using such figures can help in understanding navigation paths, especially when analyzing maps or creating route systems for transportation.
In all of these cases, the inherent properties of opposite sides being parallel help ensure reliability, strength, and visual harmony in the final product, demonstrating the wide-ranging influence of these shapes in everyday life.
Symmetry and Reflection in Parallelograms
Symmetry and reflection are fundamental concepts in geometry that play a crucial role in understanding the balance and structure of shapes. When it comes to four-sided figures with opposite sides parallel, these concepts are particularly important in determining how the shape behaves under transformations. By exploring the ways these figures exhibit symmetry, we can gain a deeper understanding of their geometric properties and their applications in real-world contexts.
In terms of symmetry, these shapes are notable for their reflective properties. They do not have rotational symmetry unless they meet additional criteria, but they do possess reflectional symmetry along certain axes. Reflection occurs when a shape is flipped across a line, creating a mirror image. For these four-sided figures, the line of reflection typically passes through the center and is parallel to either pair of opposite sides.
Key aspects of symmetry and reflection include:
- Reflection across the center: A common reflection axis runs through the center of the figure, dividing it into two symmetrical halves. This is particularly noticeable in cases where the sides are equal in length.
- Mirror symmetry: These figures can be reflected across lines that pass through their midpoints, maintaining their shape and structure in a mirrored form.
- Limited rotational symmetry: Unlike regular polygons, these shapes do not exhibit rotational symmetry unless specific conditions are met, such as all sides being equal.
Understanding these symmetrical properties is not only important in geometry but also plays a role in design, architecture, and even nature, where symmetry often reflects strength, balance, and aesthetic appeal.
Exploring the Rhombus and Rectangle
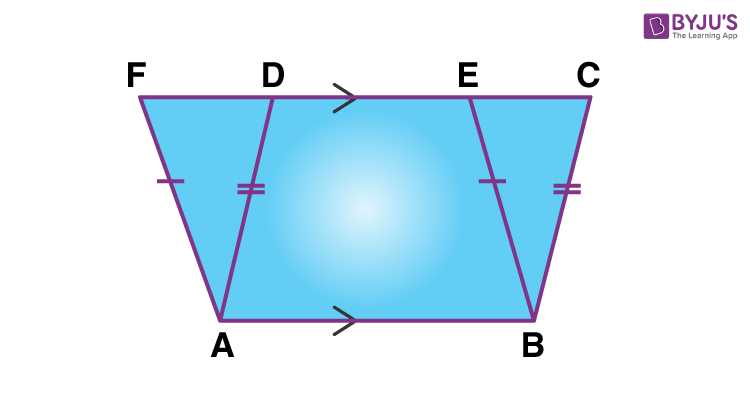
Two of the most well-known types of four-sided figures with opposite sides parallel are the rhombus and the rectangle. These shapes share certain characteristics, yet they also possess distinct qualities that differentiate them. While both are special cases of quadrilaterals with parallel sides, they each have unique attributes related to their angles, side lengths, and symmetry. Understanding the distinctions between them is key to mastering geometry and applying these concepts to real-world problems.
The Rhombus: Key Features
A rhombus is a four-sided figure where all sides are of equal length, and opposite angles are congruent. However, the angles of a rhombus are not necessarily 90 degrees. Instead, the diagonals of a rhombus intersect at right angles and bisect each other at 90 degrees, creating four right triangles within the shape. These characteristics make it a unique and visually interesting shape, often used in design and art.
- Equal side lengths: All four sides of the shape are congruent.
- Angles: Opposite angles are equal, but adjacent angles are not 90 degrees.
- Diagonal properties: The diagonals bisect each other at right angles and are not equal in length.
The Rectangle: Key Features
A rectangle, on the other hand, is a four-sided figure where all angles are right angles (90 degrees). Unlike the rhombus, the sides of a rectangle are not all equal in length, but opposite sides are congruent. This shape is especially important in geometry, engineering, and design due to its regularity and symmetry, making it one of the most commonly encountered quadrilaterals.
- Right angles: All four angles are 90 degrees.
- Opposite sides are equal: The opposite sides of a rectangle are congruent in length.
- Diagonals: The diagonals of a rectangle are equal in length and bisect each other.
While both the rhombus and rectangle belong to the broader family of quadrilaterals with parallel sides, understanding their defining characteristics–such as angles, side lengths, and diagonal relationships–helps to clarify their differences and applications in both theoretical and practical contexts.
Solving Parallelogram Problems Step by Step
When tackling problems involving four-sided figures with parallel opposite sides, a systematic approach is key to finding the correct solutions. Whether you’re dealing with angles, side lengths, or areas, breaking down the problem into smaller, manageable steps helps ensure accuracy. This approach can be applied to various problem types, from basic geometry to more complex calculations. Understanding the essential relationships and properties between sides and angles is crucial for successful problem-solving.
Step 1: Identify Given Information
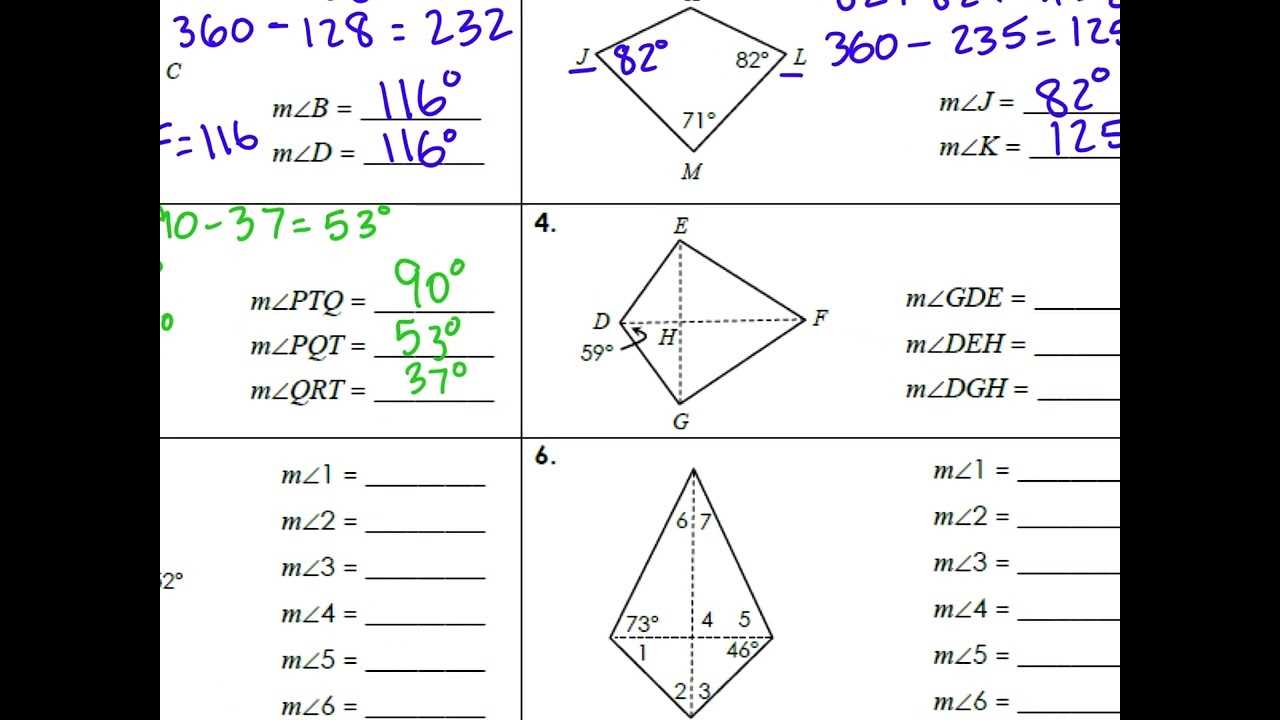
The first step in solving any problem is to clearly identify what is provided. Look for the given measurements or angles in the problem statement. This can include side lengths, angle values, or any other geometric properties that will be useful in your solution. Sometimes, a diagram is provided, which can help visualize the problem and better understand the relationships between different elements.
Step 2: Apply Known Formulas and Theorems

Next, apply the relevant geometric formulas or theorems. For example, if the problem involves calculating the area, use the formula for the area of a quadrilateral with parallel sides. Similarly, for problems involving angles, apply the theorem that opposite angles are congruent, or use the property that adjacent angles add up to 180 degrees. Always refer to the properties and relationships that hold true for the figure you’re working with.
| Formula | Use Case |
|---|---|
| Area = Base × Height | Used to calculate the area when the base and height are known. |
| Opposite sides are equal | Helpful for finding missing side lengths in problems where side pairs are equal. |
| Sum of angles = 360° | Used to check the sum of interior angles in any quadrilateral. |
Step 3: Solve for Unknown Values
Once you’ve applied the correct formulas and theorems, you’ll likely have some unknown values to solve for, such as missing side lengths or angles. Depending on the given data, you might need to set up equations and solve for these unknowns algebraically. Remember, consistency in applying the geometric rules is essential at this stage.
By following these steps systematically, you can confidently solve problems involving figures with parallel opposite sides, ensuring accurate and reliable results every time.
Advanced Properties of Parallelograms
In geometry, some quadrilaterals with parallel opposite sides possess unique and more complex characteristics that extend beyond basic definitions. These advanced features are essential when solving more intricate problems involving these shapes. Understanding these higher-level traits enables mathematicians to explore additional properties such as rotational symmetry, diagonal bisecting, and conditions for specific forms like rhombuses or rectangles. Let’s take a deeper dive into these advanced concepts.
Diagonal Properties and Bisection
One of the advanced aspects of these quadrilaterals is the relationship between their diagonals. Unlike general quadrilaterals, the diagonals of such shapes bisect each other, meaning they divide one another into two equal parts. This property is critical in various applications, including the derivation of more complex geometric proofs. In some cases, these diagonals intersect at specific angles, leading to additional geometric relationships.
Symmetry and Reflectional Features

Shapes with parallel opposite sides exhibit various symmetrical properties. They possess at least one axis of symmetry, which is crucial for both geometric design and practical applications. These figures can be reflected across the line of symmetry without changing their overall appearance. Understanding these symmetrical traits can assist in solving more advanced problems where symmetry is a key factor.
| Advanced Feature | Explanation |
|---|---|
| Diagonal Bisection | The diagonals bisect each other, dividing the figure into two equal parts. |
| Equal Opposite Angles | Opposite angles in these shapes are congruent, a crucial property in solving geometric proofs. |
| Rotational Symmetry | These figures exhibit rotational symmetry, meaning they can be rotated 180° around their center and still map onto themselves. |
| Reflectional Symmetry | At least one axis of symmetry divides the figure into two mirror-image halves. |
These advanced characteristics are essential for anyone looking to gain a deeper understanding of these geometric shapes. They form the foundation for solving complex geometry problems and contribute to the development of mathematical theories that extend beyond basic figures.