
In this section, we focus on essential skills for tackling mathematical challenges. The goal is to break down complex problems into manageable steps and find the most efficient methods for solving them. By understanding core principles and applying logical reasoning, anyone can improve their problem-solving abilities in this subject area.
Each task is designed to strengthen your grasp of important techniques and provide insight into how to approach unfamiliar questions. With consistent practice, you can learn to recognize patterns, apply relevant formulas, and develop a deeper understanding of the material. Success comes from repeated application and careful analysis of each solution.
Through this process, learners not only gain confidence in their ability to find the correct solutions but also enhance their critical thinking skills. Whether you’re preparing for exams or simply aiming to improve your grasp of the concepts, this approach will support your learning journey.
Lesson 8.2 Practice A Answer Guide
This section provides a detailed guide to solving the problems found in this particular exercise set. The objective is to break down the steps involved in reaching the correct solutions, helping you understand the reasoning behind each step. By following the outlined approach, learners can navigate through each question with confidence and clarity.
The guide covers a variety of mathematical principles, offering a comprehensive breakdown of how to apply the right techniques to each scenario. It aims to reinforce your problem-solving skills by showing you the most efficient methods and the logic that connects each concept. With practice, the goal is to gain fluency in handling different types of questions in this field.
Each explanation is designed to help you grasp the concepts at a deeper level, ensuring that you not only reach the right results but also understand how and why those results are obtained. This structured approach is essential for mastering complex tasks and advancing your knowledge in the subject.
Understanding Key Geometry Concepts
To effectively solve mathematical problems related to shapes and space, it’s essential to grasp several core ideas. These concepts lay the groundwork for a deeper understanding of spatial relationships and the properties of different figures. Mastery of these principles allows for accurate analysis and solution of complex problems.
Essential Ideas to Focus On

- Types of Figures: Understanding the characteristics of different shapes, such as polygons, circles, and solids, is fundamental. Each figure has distinct properties that are crucial for solving related problems.
- Angles and Their Types: Recognizing and categorizing angles–acute, obtuse, right–helps in various scenarios where angles influence calculations or relationships.
- Measurements and Dimensions: Mastery of how to measure sides, areas, and volumes is central to solving questions that involve real-world dimensions.
- Relationships Between Parts: Understanding how elements such as sides, angles, and diagonals interact within a shape is vital for creating accurate solutions.
Effective Problem-Solving Techniques

- Breaking Down the Problem: Identify all known elements and clarify what needs to be determined. This approach makes even the most complicated problems more manageable.
- Visualizing the Problem: Drawing diagrams or sketches helps clarify spatial relationships, turning abstract concepts into something tangible and easier to manipulate.
- Applying Core Formulas: Use formulas that apply to each specific shape or problem type to calculate unknown values, ensuring the process follows logical steps.
- Verifying the Solution: Double-check each step to ensure accuracy, ensuring that the solution aligns with the problem’s conditions.
By reinforcing these core principles and methods, you can develop a strong foundation for solving a wide variety of related tasks and mastering complex concepts.
Steps to Solve Lesson 8.2 Problems
Solving mathematical challenges involves a structured approach to ensure accuracy and efficiency. By breaking down each task into manageable steps, you can systematically work through even the most complex problems. This section provides a step-by-step guide to solving typical problems found in this exercise set, helping you improve your problem-solving skills and understand the reasoning behind each solution.
Step-by-Step Approach
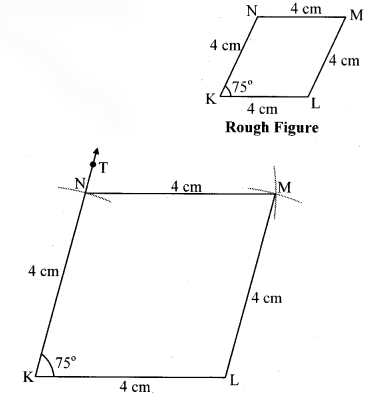
- Read the Problem Carefully: Begin by thoroughly reading the problem statement. Identify the given information and what is being asked for. This will provide the foundation for your solution.
- Visualize the Situation: If possible, draw a diagram or sketch to represent the given information. Visual aids often help clarify relationships between elements and make the problem easier to solve.
- Identify Relevant Formulas: Determine which principles or formulas apply to the problem at hand. This step ensures that you use the correct mathematical tools to solve the task.
- Break Down the Solution: Start solving step by step, applying the appropriate formulas or theorems. Break the process into smaller, manageable parts to prevent errors and ensure clarity.
- Check Your Work: After obtaining a solution, review each step and verify the calculations. Confirm that your answer makes sense within the context of the problem.
Practical Tips for Success
- Work Through Examples: Practice with similar problems to become familiar with different types of questions and solutions. The more you practice, the quicker and more accurate you’ll become.
- Stay Organized: Keep your work neat and well-organized. Writing each step clearly will prevent confusion and reduce the chances of mistakes.
- Take Your Time: Rushing through problems can lead to careless errors. Be patient and methodical in your approach to ensure accuracy.
By following these steps and tips, you’ll be able to approach any related problem with confidence and improve your overall understanding of the concepts.
Common Mistakes to Avoid in Geometry
When tackling problems related to shapes and spatial reasoning, it’s easy to fall into certain traps that can lead to incorrect solutions. Identifying and avoiding these common mistakes is crucial to improving your skills and achieving accurate results. This section highlights some of the most frequent errors students make and provides tips on how to prevent them.
Frequent Errors in Problem Solving
- Misunderstanding Given Information: Always carefully read the problem to ensure you fully understand what is being asked and the information provided. Skipping this step can lead to applying incorrect formulas or assumptions.
- Incorrect Use of Formulas: Applying the wrong formula or using it inappropriately is a common mistake. Double-check that you are using the correct equation for the specific shape or relationship in question.
- Forgetting to Label Diagrams: Diagrams are a valuable tool, but they can be misleading if not properly labeled. Make sure to mark all relevant angles, sides, and points clearly to avoid confusion later in the process.
- Rushing Calculations: Hurrying through the math can lead to simple arithmetic errors. Take your time and verify each calculation to ensure accuracy.
- Confusing Angle Relationships: When working with angles, be sure to correctly identify whether they are complementary, supplementary, or vertical. Misinterpreting these relationships can lead to incorrect results.
How to Avoid These Mistakes
- Double-Check Your Work: Always revisit your calculations and reasoning to ensure each step is correct. A second look often reveals small mistakes that can be easily fixed.
- Practice Regularly: The more you practice, the more familiar you become with the common pitfalls. Repetition builds confidence and reduces the likelihood of making mistakes.
- Ask for Clarification: If you’re unsure about a particular concept or problem, don’t hesitate to ask for help or consult additional resources. A clear understanding is key to avoiding errors.
- Work Step-by-Step: Avoid jumping ahead to conclusions. Working through each step methodically ensures you stay on track and reduces the risk of overlooking important details.
By being aware of these common mistakes and implementing these strategies, you’ll improve your problem-solving abilities and minimize errors in your work.
How to Approach Geometry Word Problems

Word problems in mathematics can often seem overwhelming due to the amount of information they provide and the abstract nature of the questions. However, by breaking down the problem and approaching it systematically, you can transform a seemingly complex challenge into a manageable task. This section outlines the key steps to effectively tackle word problems and derive solutions with confidence.
Steps to Solve Word Problems
- Read the Problem Carefully: Start by reading the problem multiple times to ensure you fully understand what is being asked. Identify the important details and note any specific measurements or relationships mentioned.
- Visualize the Situation: If possible, draw a diagram that represents the scenario. A well-labeled sketch can help clarify the problem and make it easier to identify the relevant mathematical concepts.
- Identify the Known and Unknown: Clearly distinguish what information is given and what needs to be found. Organize the known values and assign variables to the unknown quantities, if applicable.
- Translate Words into Math: Convert the word problem into mathematical expressions or equations. Look for keywords such as “sum,” “difference,” “product,” or “quotient” that signal specific operations.
Tips for Success
- Work Step-by-Step: Break the problem into smaller, more manageable steps. Solving each part of the problem gradually makes it easier to stay organized and reduces the chance of making errors.
- Check for Units: Ensure all units are consistent throughout the problem. Convert measurements if necessary, and double-check that your final answer matches the required units.
- Review and Verify: Once you’ve arrived at a solution, go back and review each step. Verify that the answer makes sense and aligns with the context of the problem.
By following these steps and practicing regularly, you’ll become more proficient at handling word problems and applying mathematical concepts in real-world situations.
Important Theorems in Geometry Practice
Understanding and applying foundational theorems is essential for solving mathematical problems involving shapes, lines, and angles. These theorems provide the necessary principles for deriving solutions to complex questions and forming logical connections between various geometric elements. This section explores key theorems and their applications, helping you strengthen your problem-solving skills.
Key Theorems and Their Applications
- Triangle Sum Theorem: The sum of the interior angles of any triangle is always 180°. This fundamental theorem is frequently used to find unknown angles in triangles.
- Pythagorean Theorem: In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. This theorem is vital for solving problems involving right-angled triangles.
- Parallel Line Theorems: If two lines are parallel and are cut by a transversal, several angle relationships hold true, such as corresponding angles being equal and alternate interior angles being congruent.
- Congruence and Similarity Theorems: These theorems, such as SSS (Side-Side-Side), SAS (Side-Angle-Side), and AA (Angle-Angle), allow you to determine when two shapes are congruent or similar based on their angles and side lengths.
- Angle Bisector Theorem: This theorem states that the angle bisector of an angle in a triangle divides the opposite side into segments that are proportional to the other two sides of the triangle.
How to Apply These Theorems
- Identify the Problem Type: Recognize which theorems apply based on the shapes and relationships in the problem. Look for clues like right angles, parallel lines, or congruent sides.
- Use Theorems Step-by-Step: Apply the theorems in the correct order to derive unknown values. For instance, use the Pythagorean Theorem to find a missing side in a right triangle, then apply the Triangle Sum Theorem to find missing angles.
- Check Consistency: After applying a theorem, verify the results by checking if they make sense with the given information. Ensure your calculations align with the problem’s conditions.
Mastering these key theorems and knowing how to apply them will enhance your ability to solve a wide variety of problems with confidence and precision.
Tips for Mastering Geometric Proofs

Proving relationships between shapes, lines, and angles is a crucial skill in mathematics. Geometric proofs require logical reasoning, careful organization of information, and a solid understanding of established principles. By mastering this skill, you can approach complex problems with confidence and precision. This section provides valuable tips to help you excel in constructing and solving geometric proofs.
Effective Strategies for Proofs
- Understand the Given Information: Carefully analyze the problem and identify the known facts. Understanding what is provided is essential for developing a clear plan of action.
- Break the Problem into Steps: Start by outlining your approach and breaking the proof into smaller, more manageable steps. This makes it easier to organize your reasoning and ensures you don’t miss any crucial details.
- Use Definitions and Postulates: Make sure to apply definitions, postulates, and previously proven theorems. These are the foundation of logical reasoning in proofs and are necessary for reaching the correct conclusion.
- Draw Accurate Diagrams: Visualize the problem by drawing a clear, accurate diagram. Label all known points, lines, and angles to help guide your proof and avoid any confusion.
- Keep the Proof Organized: Present each step clearly and logically. Ensure each conclusion flows from the previous one, and always justify each step with a valid reason, such as a definition or theorem.
Common Techniques in Proofs

| Technique | Description |
|---|---|
| Direct Proof | Start with the known facts and use logical steps to arrive at the desired conclusion. |
| Proof by Contradiction | Assume the opposite of what you need to prove, and show that this assumption leads to a contradiction. |
| Two-Column Proof | Present the steps of the proof in two columns: one for the statements and another for the justifications or reasons. |
| Inductive Reasoning | Make a conjecture based on observed patterns and use it to prove general cases. |
By following these strategies and practicing regularly, you’ll gain the ability to construct well-reasoned and logical proofs that are clear and convincing. Geometric proofs may seem challenging at first, but with persistence and careful attention to detail, you can master them effectively.
Breaking Down Lesson 8.2 Questions
When approaching complex mathematical problems, it’s essential to break them down into manageable parts. By identifying the key elements of each question, you can develop a clear plan for solving it step by step. This section focuses on how to dissect and analyze problems effectively to make the solving process smoother and more efficient.
The first step is to carefully read the question multiple times to understand the underlying problem. Identify all the information provided, such as measurements, relationships between elements, or any specific conditions mentioned. Then, determine what needs to be found or proven. This helps you focus on what is most relevant and prevents unnecessary confusion during problem-solving.
Next, it’s important to visualize the problem. Drawing a diagram or sketch can help clarify the relationships between different parts of the problem. Label all known information on the diagram and use appropriate symbols to represent unknown values. This visual representation can often make it easier to identify patterns or connections that are not immediately obvious from the text alone.
Once you have a clear understanding of the problem, organize your solution approach. Break the problem down into smaller, logical steps, each building upon the previous one. Ensure that each step follows a clear, logical progression, whether you’re applying a specific theorem or performing a calculation. Staying organized helps to avoid errors and ensures that no crucial details are overlooked.
By following these steps and practicing regularly, you’ll develop the skills to efficiently tackle even the most challenging problems. Breaking down questions not only improves problem-solving efficiency but also enhances your overall understanding of the material.
Geometry Vocabulary to Know
Understanding the basic terminology is crucial when working with shapes, angles, and other related concepts. The right vocabulary helps clarify communication and ensures you can apply concepts accurately. Familiarizing yourself with the essential terms will make it easier to approach problems and develop solutions efficiently. Here are some key terms to keep in mind when studying the subject.
First, it’s important to grasp the meaning of common elements such as lines, angles, and shapes. These are the building blocks of more complex problems. Other terms like perpendicular and parallel describe the relationship between lines, while congruent refers to objects that are identical in shape and size.
Another critical area of vocabulary includes the various polygons like triangles, squares, and rectangles. Understanding the specific properties of each type, such as the number of sides, angles, and symmetry, is essential for solving related problems. Terms like vertex and diagonal also come up frequently when working with polygons.
Additionally, concepts related to measurements, such as area, perimeter, and volume, are essential for determining the size of objects or spaces. These terms are used to calculate the size of various figures in both two-dimensional and three-dimensional contexts. Mastering these terms will help you navigate complex mathematical scenarios with ease.
Having a solid grasp of these terms allows for smoother problem-solving and more effective communication, ensuring you can tackle a wide range of tasks in the subject.
How to Verify Your Geometry Solutions
After solving a mathematical problem, it’s important to check your work to ensure the solution is correct. Verification helps identify any mistakes and ensures that all steps were followed properly. The process involves reviewing both the logic behind the solution and the calculations used to reach the final result. In this section, we will explore methods to verify solutions and confirm the accuracy of your work.
The first step in verifying your solution is to review the problem statement. Carefully read the question again to make sure you haven’t missed any key information or misunderstood the problem. Identify the goal of the question, whether it’s to find a specific measurement, prove a relationship, or demonstrate a property. Reconfirm that you are answering exactly what is asked.
Double-Check Your Work

Next, go through your solution step by step. Check each calculation to ensure there are no arithmetic mistakes, such as incorrect addition or subtraction. If you applied any formulas, verify that they are the correct ones for the given situation. If you used geometric properties, confirm that they are applied correctly. It can be helpful to retrace your work from start to finish, ensuring that each logical step flows into the next.
Use Alternative Methods
Another way to verify your solution is to use a different method to arrive at the same result. For example, if you solved a problem using algebraic equations, try using a geometric approach to see if you get the same outcome. Alternatively, if a diagram was involved, check that your drawing is accurate and all labeled measurements are correct. Using different methods helps to confirm that the solution is not just a coincidence but is indeed correct.
Finally, it’s a good idea to consult known theorems or properties related to the problem. For example, if the problem involves triangles, use well-known properties like the Pythagorean theorem or angle sum properties to double-check your results. If you are working with shapes, ensure that the properties of those shapes (such as symmetry or congruence) are properly utilized.
| Method | Action |
|---|---|
| Step-by-Step Review | Recheck each calculation and verify the logic used. |
| Alternative Approach | Use a different method or formula to solve the same problem. |
| Use Theorems | Apply relevant properties or theorems to cross-check results. |
By carefully verifying your solutions through these methods, you can ensure that your answers are accurate and reliable. This will help build your confidence and reduce errors in future problem-solving tasks.
Strategies for Geometry Test Success
Achieving success on a mathematics test requires more than just understanding the concepts; it involves using the right strategies before, during, and after the exam. By approaching each task with a clear plan, staying organized, and maintaining focus, you can improve your chances of performing well. In this section, we will explore effective methods to help you excel when tackling complex problems on a test.
One of the most crucial strategies is to thoroughly prepare in advance. This means reviewing key principles, solving a variety of practice questions, and testing your understanding with mock exams. The more you familiarize yourself with the types of problems you might encounter, the more confident you’ll feel during the actual test. Setting aside regular study sessions is an excellent way to ensure you’re ready when the time comes.
Master the Core Concepts
Before diving into practice problems, make sure you have a strong grasp of the fundamental concepts. Understand the properties of shapes, how to calculate area and volume, and the relationships between angles and sides. These building blocks form the foundation for solving more complex problems and will help you recognize patterns and apply the right methods quickly during the test.
Manage Your Time Effectively
Time management is another vital aspect of success. Many tests have a time limit, so it’s essential to pace yourself. Start by quickly scanning the entire exam to identify questions that seem easier and tackle those first. This ensures you can complete the easier tasks before moving on to more challenging ones. If you get stuck on a problem, don’t waste too much time–move on and come back to it later if needed.
| Strategy | Action |
|---|---|
| Preparation | Review key concepts, practice problems, and take mock tests. |
| Core Concepts | Master fundamental properties, formulas, and relationships. |
| Time Management | Pace yourself by completing easier questions first and returning to harder ones. |
Finally, don’t forget to review your work at the end of the test. If time allows, go over your answers to ensure there are no simple mistakes or missed steps. This final check can often catch errors you might have overlooked during the initial solving process. Implementing these strategies will increase your chances of success and help you feel more confident when taking your test.
Review of Key Formulas in Geometry
When studying shapes, measurements, and spatial relationships, it’s essential to familiarize yourself with the fundamental equations that govern these areas. These formulas serve as tools to calculate various attributes such as area, perimeter, volume, and angles. Mastering them allows you to approach problems with confidence and accuracy, making it easier to solve complex questions. In this section, we will review some of the most important equations you’ll encounter in this field.
Area and Perimeter Formulas
Understanding how to calculate the area and perimeter of basic shapes is essential. Here are the key formulas:
- Rectangle: Area = length × width, Perimeter = 2(length + width)
- Triangle: Area = 1/2 × base × height, Perimeter = sum of all sides
- Circle: Area = π × radius², Circumference = 2 × π × radius
Volume and Surface Area Formulas
For 3D objects, knowing how to compute volume and surface area is equally important. Here are the formulas for some common solids:
- Cube: Volume = side³, Surface Area = 6 × side²
- Cylinder: Volume = π × radius² × height, Surface Area = 2π × radius × (height + radius)
- Sphere: Volume = 4/3 × π × radius³, Surface Area = 4π × radius²
By committing these formulas to memory and practicing their application, you’ll be better prepared to tackle problems involving various shapes and objects. These fundamental equations are the building blocks for solving more advanced concepts in this subject area.
Working with Geometric Shapes Effectively
To excel in solving problems involving figures and their properties, it is crucial to understand how to manipulate and work with various forms. Each shape has its own unique characteristics that, when fully grasped, can lead to more efficient problem-solving strategies. This section will guide you through effective methods for approaching shapes and their associated calculations, helping you build a stronger foundation in the subject.
Analyzing Key Properties
Before solving any problem involving shapes, always begin by analyzing their fundamental properties. These may include:
- Angles: Know the relationship between angles within different polygons, such as interior and exterior angles.
- Sides: Understand how the number of sides impacts properties like symmetry, perimeter, and area.
- Symmetry: Recognizing symmetrical shapes can simplify calculations and help visualize solutions more clearly.
Efficient Calculation Strategies
Once you understand the properties of a shape, the next step is applying the right formulas and strategies. Here are a few key tips:
- Break Complex Shapes into Simpler Parts: For irregular shapes, divide them into familiar ones (like triangles or rectangles) to make calculations easier.
- Use Units Consistently: Ensure that all measurements are in the same units before starting calculations, and convert where necessary.
- Visualize: Drawing out a shape, labeling known values, and marking key angles can often make it easier to identify relationships and solve for unknowns.
By practicing these techniques regularly, you’ll not only improve your efficiency but also deepen your understanding of how different shapes interact within mathematical contexts.
Understanding the Role of Angles
Angles are fundamental components in the study of shapes and their properties. They provide important information about the relationship between lines, surfaces, and the space within them. Understanding how angles function in various contexts can significantly enhance your problem-solving skills, whether you’re dealing with simple figures or more complex structures. This section explores the importance of angles and how they affect geometric reasoning.
Types of Angles
In geometry, different types of angles serve various purposes. Recognizing these different types is key to understanding their roles in geometric problems. Common angle types include:
- Acute Angles: Angles less than 90 degrees, often encountered in sharp corners.
- Right Angles: Angles exactly equal to 90 degrees, frequently found in squares, rectangles, and many other polygons.
- Obtuse Angles: Angles greater than 90 degrees but less than 180 degrees, often seen in open shapes.
- Reflex Angles: Angles greater than 180 degrees but less than 360 degrees, typically encountered in circles and rotational problems.
Angle Relationships and Their Importance
Angles don’t exist in isolation; they interact in various ways to form larger geometric structures. Here are a few critical relationships:
- Complementary Angles: Two angles that add up to 90 degrees, often used in right-angle problems.
- Supplementary Angles: Two angles that add up to 180 degrees, typically seen in linear pairs.
- Vertical Angles: Angles opposite each other when two lines intersect; these angles are always congruent.
- Adjacent Angles: Two angles that share a common side and vertex but don’t overlap, frequently used in polygons and angle sums.
Mastering these angle relationships allows you to identify and solve problems more effectively. Whether you are calculating areas, determining angles in polygons, or solving complex proofs, understanding angles is essential to achieving success in the subject.
Geometry Problem-Solving Techniques
Effective problem-solving in geometry requires a combination of strategic approaches and a clear understanding of mathematical principles. Whether you’re tackling simple or complex problems, the key to success lies in applying systematic techniques that help break down the task at hand. In this section, we’ll explore some of the most effective strategies to solve geometric challenges efficiently and accurately.
Key Approaches for Solving Problems
By applying specific methods and focusing on essential properties, you can simplify even the most intricate problems. Some of the most useful techniques include:
- Draw Diagrams: Visualizing the problem by drawing diagrams can make it easier to identify the key elements, such as angles, sides, and intersections.
- Use Known Theorems: Theorems such as the Pythagorean theorem, triangle inequality, and angle sum properties provide critical insight into solving unknowns.
- Break Complex Problems into Parts: Large, complex problems can often be simplified by solving smaller, manageable sections first and then combining them to find the overall solution.
- Look for Symmetry: Symmetry often reveals patterns that simplify calculations and help identify equivalent elements within a figure.
Common Techniques for Specific Problem Types
Different types of geometric problems require tailored approaches. Below are some common techniques for specific challenges:
- Finding Area or Perimeter: Use basic formulas for common shapes (e.g., triangles, rectangles, and circles) and apply them correctly by identifying the necessary measurements.
- Working with Angles: When dealing with angles, leverage properties such as complementary and supplementary angles, as well as angle bisectors, to simplify calculations.
- Proofs and Logical Reasoning: In proof-based problems, establish known facts and build step-by-step logical connections to reach the desired conclusion. Use direct proofs, indirect proofs, or proof by contradiction as needed.
- Coordinate Geometry: In coordinate-based problems, apply distance and midpoint formulas, as well as slopes and equations of lines, to solve problems related to points and figures on the coordinate plane.
By mastering these techniques and regularly practicing problem-solving, you can improve both your understanding and performance in solving geometric problems. Developing a strong foundation in these approaches will not only help in solving specific problems but will also build critical thinking skills applicable to other areas of mathematics.
How Practice A Improves Geometry Skills
Engaging in focused exercises plays a crucial role in enhancing mathematical abilities. Regular practice helps strengthen fundamental concepts and sharpens problem-solving techniques. By consistently working through a variety of tasks, learners gain confidence and proficiency in applying theoretical knowledge to real-world scenarios. In this section, we will explore how repetitive exercises can significantly boost one’s competence in spatial reasoning and logical deduction.
The Benefits of Consistent Practice
Repetition fosters familiarity and aids in mastering the core principles. Below are some key ways in which consistent exercises contribute to skill development:
- Strengthens Conceptual Understanding: Repeated exposure to different problems solidifies the understanding of essential principles, making it easier to recognize patterns and relationships within figures.
- Enhances Problem-Solving Efficiency: With each new challenge, learners develop quicker, more effective methods for solving similar tasks. This leads to faster, more accurate solutions in future exercises.
- Builds Confidence: Mastering a variety of problems through continuous effort boosts self-assurance. As learners solve more complex issues, they become less apprehensive about tackling new, unfamiliar tasks.
- Improves Retention: Active involvement through hands-on exercises strengthens long-term retention of concepts. Repetition helps shift knowledge from short-term to long-term memory, ensuring the concepts stick.
Types of Exercises That Maximize Skill Development
Not all exercises are created equal; certain types are particularly effective in promoting deeper comprehension and stronger abilities. Consider the following methods for optimal improvement:
- Worked Examples: Reviewing step-by-step solutions to similar problems helps learners understand the logical flow of problem-solving techniques and apply them independently.
- Challenge Problems: Tackling more complex or multi-step questions pushes learners to think critically and explore different strategies, further expanding their skill set.
- Timed Exercises: Practicing under time constraints helps improve speed and accuracy. This can be especially useful when preparing for exams or real-world applications that require quick thinking.
- Concept Reinforcement: Revisiting problems that specifically target a single concept ensures mastery over key ideas. Focused practice aids in solidifying weak areas of understanding.
Ultimately, continuous engagement with different types of exercises not only enhances the ability to solve problems but also strengthens the overall analytical mindset. As learners become more accustomed to handling a range of scenarios, their ability to approach new problems with clarity and confidence increases, leading to long-term success in mathematical endeavors.
Preparing for Quizzes and Exams
Proper preparation is essential for success in any test that involves spatial reasoning and logical problem-solving. By reviewing essential concepts, practicing problem-solving techniques, and managing your study time effectively, you can significantly improve your performance. The key to excelling in these assessments lies in a structured study approach that helps you retain information and apply it accurately under timed conditions.
Effective Study Techniques
Here are some useful study methods to maximize your preparation:
- Understand Fundamental Concepts: Ensure that you have a clear grasp of the core principles and definitions, such as the properties of shapes, angles, and theorems, which are central to solving problems.
- Work Through Practice Problems: Apply what you’ve learned by solving a wide range of problems. The more problems you solve, the more familiar you will become with the types of questions that are likely to appear.
- Use Study Tools: Create diagrams, charts, and other visual aids to enhance your understanding of complex concepts. Visualizing problems can often help you solve them more effectively.
- Time Yourself: During your study sessions, time yourself while solving problems to simulate the conditions of a real test. This will help you improve both your speed and accuracy.
Time Management for Maximum Efficiency
Time management is crucial when preparing for any test. Below is a table outlining effective strategies to make the most of your study time:
| Strategy | Purpose |
|---|---|
| Set a Study Schedule | Breaking down the material into manageable chunks and allocating specific time slots for each section helps you stay organized. |
| Review Past Mistakes | Look at previous errors to identify areas that need more focus. This ensures you don’t repeat the same mistakes. |
| Take Regular Breaks | Short breaks during study sessions help maintain concentration and prevent burnout, allowing you to study more effectively. |
| Simulate Test Conditions | Taking mock tests under timed conditions helps reduce anxiety and allows you to practice answering questions within the allotted time frame. |
By following these strategies and maintaining a consistent study schedule, you will feel more confident and well-prepared on the day of the exam. Success in any assessment comes from understanding the material, honing your problem-solving skills, and managing your time wisely. With a structured approach, you can master the concepts and excel in your tests.