
In fifth grade, students dive into more complex problem-solving and critical thinking challenges, requiring a solid understanding of core topics. As they progress, they face new concepts that can sometimes be difficult to grasp, making it crucial for them to have the right resources to support their learning journey. One of the most valuable tools for students and educators alike is a comprehensive guide that breaks down these concepts clearly and effectively.
By working through detailed solutions and explanations, students can strengthen their grasp on fundamental skills that will serve as the foundation for future learning. Whether they are reviewing past lessons or tackling new material, having a structured approach helps them build confidence and mastery. With the right guidance, complex problems become manageable and engaging, ensuring a smoother path to academic success.
Parents and teachers can also benefit from using these resources, as they provide insights into the methods and strategies that lead to effective learning outcomes. Being able to reference detailed examples encourages a deeper understanding, making the learning process both enjoyable and efficient.
Understanding Core Concepts in Fifth Grade
At this stage of learning, students encounter more advanced topics that build on the foundation laid in earlier years. The focus shifts toward developing critical thinking and problem-solving skills, which are essential for tackling complex tasks. Understanding the concepts taught at this level is key to ensuring that students are prepared for future challenges and can connect different ideas effectively.
The curriculum introduces a variety of subjects that require students to apply both their reasoning and computational abilities. These subjects are designed to foster a deeper understanding of mathematical relationships and develop skills that will be essential for higher-level learning. With structured lessons and carefully crafted exercises, the material encourages students to explore concepts through practical examples and hands-on practice.
Teachers and students alike benefit from having clear and accessible explanations to guide them through these complex topics. By providing step-by-step solutions and detailed breakdowns, students gain a stronger command of the material and are better equipped to handle progressively challenging problems. Through consistent practice and review, learners are empowered to achieve mastery in these critical subjects.
Overview of Module 4 Concepts
This section of the curriculum focuses on advancing the skills necessary to solve more intricate problems. Students are introduced to new strategies that help deepen their understanding of key principles. The content encourages critical thinking and provides the tools to approach complex tasks with greater confidence and precision.
Building on Previous Knowledge
As learners move through this section, they apply previously learned concepts in more sophisticated ways. Emphasis is placed on strengthening problem-solving techniques and refining the ability to break down multi-step questions. This progression allows students to approach problems from multiple angles, improving their adaptability and flexibility in thinking.
Key Topics Explored
Throughout the lessons, students explore a range of important topics, including fraction operations, decimal comparison, and multi-digit calculations. These areas are presented through interactive examples and practice exercises that encourage both conceptual understanding and practical application. The goal is to ensure that learners not only grasp the theory but also gain confidence in applying their knowledge to real-world scenarios.
Key Topics in Fifth Grade Learning
The curriculum at this level covers a wide array of essential subjects that help students develop a deeper understanding of foundational concepts. These topics build on prior knowledge while introducing new challenges that encourage students to think critically and apply their skills in more complex situations. By focusing on key areas, the content aims to equip students with the tools necessary for solving problems and making connections between different mathematical ideas.
Operations with Fractions
A major focus of this level is on working with fractions, particularly adding, subtracting, multiplying, and dividing them. Students learn how to handle fractions with unlike denominators and how to apply these operations to real-world scenarios. Mastery of these concepts is essential for future success in more advanced mathematics.
Decimals and Place Value
Understanding decimal numbers and their place value is another core area. Students explore how to perform operations with decimals and how to compare and round them. The ability to work with decimals in everyday situations, such as money or measurement, helps students solidify their understanding of number concepts and prepares them for more advanced topics.
How to Use the Answer Guide
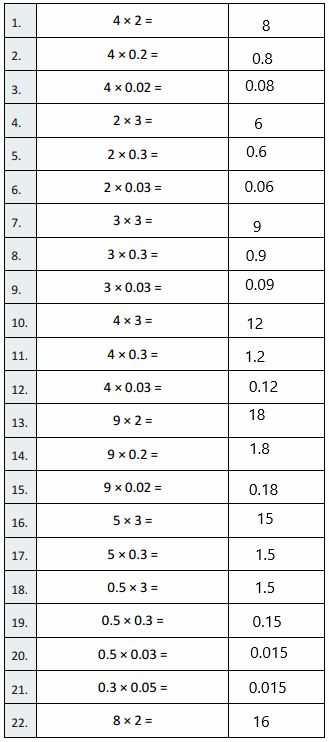
The answer guide is an invaluable tool that helps students and educators track progress and understand where mistakes may have occurred. It provides clear solutions to exercises and serves as a reference for explaining complex problems. By using this resource effectively, learners can gain a deeper understanding of the material, correct errors, and reinforce their comprehension of key concepts.
Step-by-Step Problem Solving
When using the guide, start by reviewing the provided solutions to each problem. Focus on how each step is approached and note any strategies or methods that can be applied to similar questions. This will not only help students find the correct solutions but also improve their problem-solving skills over time.
Identify and Understand Mistakes
If a mistake is made, the guide offers an opportunity to identify where things went wrong. Compare the student’s approach to the provided solution and pinpoint any missteps. Understanding these errors is critical for developing stronger reasoning and avoiding the same mistakes in the future.
Common Challenges in Module 4
As students progress through this section, they often face a variety of difficulties that can hinder their understanding of more advanced concepts. The content is designed to stretch their cognitive abilities, but certain areas tend to be more challenging than others. Identifying and addressing these obstacles early on can help learners navigate the material with greater ease and confidence.
Handling Complex Fraction Operations
One of the most common challenges in this section is dealing with complex operations involving fractions. Students are required to add, subtract, multiply, and divide fractions with unlike denominators. These tasks can be overwhelming without a strong grasp of the underlying principles, making it essential to practice consistently and break down each step methodically.
Understanding Decimal Conversions
Another area that often causes confusion is converting between fractions and decimals. While the concept seems straightforward, many students struggle with accurately converting and comparing the two. It’s important to reinforce these skills through repetition and visual aids, as understanding decimal places and their relationships to fractions is crucial for success in more advanced topics.
Step-by-Step Solutions Explained
Breaking down complex problems into smaller, more manageable steps is an essential skill for mastering challenging topics. By following a structured approach to problem solving, students can better understand the logic behind each calculation or decision, which leads to greater retention and confidence. Step-by-step solutions not only help clarify difficult concepts but also guide learners through the process of applying their knowledge correctly.
Approaching the Problem
The first step in solving any problem is to carefully read and understand the question. Often, students jump straight into solving without fully grasping the problem. Here’s how to break it down:
- Read the problem carefully: Identify key information and what is being asked.
- Visualize the problem: Draw a diagram, chart, or use other tools to make the information clearer.
- Plan your approach: Decide which method or formula to use based on the problem type.
Step-by-Step Solution Process
Once you’ve planned your approach, proceed through the solution in an organized manner:
- First Step: Apply the chosen method to the first part of the problem.
- Second Step: Continue solving, making sure to perform each operation correctly and in the right order.
- Third Step: Double-check your calculations and ensure that each step follows logically from the previous one.
- Final Step: Review the answer to ensure it makes sense and answers the original question.
By consistently following this process, students can develop strong problem-solving habits and avoid common errors.
Important Strategies for Success
Achieving success in challenging academic topics requires more than just understanding the material–it involves adopting effective strategies that enhance learning and retention. By employing the right techniques, students can boost their problem-solving abilities, stay organized, and approach complex tasks with confidence. These strategies focus on both the process of learning and the habits that lead to mastery of difficult concepts.
Active Practice and Review
Consistent practice is key to mastering any subject. By regularly working through exercises and revisiting topics, students reinforce their understanding and prevent concepts from becoming unclear over time. Active review, such as solving similar problems or explaining solutions aloud, helps solidify learning and identify areas that need more attention.
Breaking Down Complex Tasks
One of the most effective techniques is breaking complex problems into smaller, manageable tasks. Instead of trying to solve everything at once, students should tackle each step individually, focusing on one aspect of the problem before moving to the next. This not only prevents overwhelm but also allows for a clearer understanding of each part of the process.
Focus on Fractions and Decimals
Understanding fractions and decimals is a crucial part of advancing in many mathematical concepts. These two topics often present challenges but are foundational for solving more complex problems. Mastering fractions and decimals provides students with the ability to make sense of real-world scenarios such as measurements, money, and data analysis. In this section, we will break down the key concepts and offer strategies to build a strong understanding of these essential topics.
Working with Fractions
Fractions represent a part of a whole, and being able to manipulate them is a critical skill. The key to mastering fractions lies in understanding how to perform operations such as addition, subtraction, multiplication, and division with them. Here are some essential points to keep in mind:
- Common Denominators: When adding or subtracting fractions, it is important to have the same denominator.
- Multiplying Fractions: Multiply the numerators together and the denominators together.
- Dividing Fractions: Invert the second fraction (take the reciprocal) and multiply.
Understanding Decimals

Decimals are another way to represent parts of a whole, and understanding their relationship to fractions is essential. Decimals are often used in real-world contexts like money or measurements, so proficiency in working with them is necessary. Here are some helpful tips:
- Place Value: Each place to the right of the decimal point represents a power of ten (tenths, hundredths, thousandths, etc.).
- Converting Fractions to Decimals: Divide the numerator by the denominator.
- Operations with Decimals: When adding or subtracting, align the decimal points. For multiplication, multiply as usual and adjust the decimal place.
What to Do with Incorrect Answers
Making mistakes is an inevitable part of the learning process, and incorrect solutions provide valuable opportunities for growth. Rather than seeing errors as setbacks, they should be viewed as stepping stones toward improvement. By analyzing why a mistake was made, students can identify gaps in their understanding and work toward mastering the material more effectively.
When faced with an incorrect solution, the first step is to review the process step by step. Understanding where the error occurred is essential to correcting it. In some cases, the mistake may be a simple miscalculation, while in others, the underlying concept may need further clarification. Taking the time to retrace your steps helps reinforce the correct approach and ensures that similar errors are avoided in the future.
Additionally, it is helpful to practice the problem again after identifying the mistake. By reworking the exercise, students can test their understanding and build confidence in their ability to solve similar problems correctly. Seeking help from a teacher, tutor, or peer is also an effective strategy for gaining clarity on difficult concepts and ensuring that mistakes are not repeated.
Practical Tips for Parents and Tutors
Supporting students in their academic journey can be challenging, but with the right strategies, parents and tutors can play a significant role in helping them succeed. Providing a structured environment, encouraging curiosity, and offering guidance during tough topics are key components of effective learning support. The following tips aim to enhance understanding, build confidence, and foster a positive learning experience.
First and foremost, creating a quiet and organized study space is essential. A distraction-free environment allows the student to focus and tackle problems with minimal interruptions. Additionally, establishing a consistent routine helps the student stay on track and manage time effectively, ensuring they make steady progress with their learning.
Encourage students to actively engage with the material by asking questions, explaining concepts in their own words, and working through problems step by step. This promotes deeper understanding and strengthens problem-solving skills. Moreover, showing patience and understanding when mistakes are made helps build resilience and boosts the student’s confidence to keep trying without fear of failure.
Lastly, when a student struggles with a concept, don’t hesitate to break it down into smaller, manageable parts. Sometimes, a different perspective or a simple explanation can make a big difference in understanding. Collaborating with the student in a positive and supportive manner reinforces that learning is a process, and mistakes are a natural part of that process.
Enhancing Understanding with Practice
Consistent practice is one of the most effective ways to deepen understanding and reinforce newly learned concepts. By regularly engaging with the material, students not only solidify their knowledge but also develop problem-solving skills and increase their confidence. Practice allows for the identification of patterns, the refinement of techniques, and a stronger grasp of complex topics. In this section, we will explore how focused repetition and varied exercises can help improve mastery and retention.
Importance of Regular Practice
Repetition is key to reinforcing what has been learned. Regularly working through similar problems helps students recognize patterns and relationships within the content. The more a student practices, the more automatic their understanding becomes, making it easier to apply knowledge in different contexts. For example, if a student repeatedly works on fraction problems, they will become more adept at recognizing different forms and solving them more efficiently.
Varying the Practice Tasks
Incorporating a variety of practice tasks can be beneficial in mastering a topic. While repetition of similar problems is helpful, varying the format and difficulty level challenges the brain to approach problems from different angles. This variety encourages deeper learning and prevents the material from feeling monotonous. Below is a sample table showing different types of practice activities:
| Practice Type | Description | Benefits |
|---|---|---|
| Simple Problems | Basic exercises that focus on one concept at a time. | Builds foundational understanding and confidence. |
| Word Problems | Real-life scenarios that require applying concepts to solve. | Improves critical thinking and problem-solving skills. |
| Timed Drills | Quick exercises with a focus on speed and accuracy. | Enhances fluency and helps identify weak areas. |
| Group Practice | Collaborative exercises where students solve problems together. | Encourages peer learning and sharing of strategies. |
By mixing different types of practice, students can enhance their ability to apply concepts in various situations, leading to better overall understanding and stronger retention of knowledge.
How Module 4 Connects to Future Lessons
Understanding the concepts covered in this section is crucial not only for mastering current material but also for building a solid foundation for future learning. The skills and strategies developed here serve as stepping stones for more advanced topics that students will encounter as they progress. The lessons learned in this unit directly relate to and support the comprehension of future subjects, ensuring a cohesive and interconnected learning experience.
Building a Strong Foundation
The concepts introduced in this unit focus on fundamental skills that will be repeatedly used in future lessons. By thoroughly understanding these basics, students are better equipped to handle more complex challenges later on. For example, mastering operations with fractions and decimals now will make it easier to tackle advanced problems involving percentages or ratios in the next units. The foundation built here enables smoother transitions into more difficult material without feeling overwhelmed.
Application in Real-World Scenarios
As students progress in their studies, the ability to apply learned concepts to real-world situations becomes increasingly important. The knowledge gained in this section helps students see the relevance of mathematical principles in everyday life. From understanding financial concepts to solving problems related to measurements and data analysis, the skills developed in this section will be essential for handling more practical, real-life scenarios in future lessons.
Interactive Learning Approaches
Engaging students through interactive methods is one of the most effective ways to reinforce concepts and promote deeper understanding. Rather than passively receiving information, students become active participants in their learning, which enhances retention and application of knowledge. Interactive learning encourages critical thinking, problem-solving, and collaboration, all of which are key components in mastering challenging topics.
These methods provide students with opportunities to engage directly with content through hands-on activities, games, and group discussions. In turn, students can experiment with concepts, make mistakes, and receive immediate feedback, which fosters a deeper connection to the material. Below is a table showcasing various interactive learning approaches that can be applied to enhance the educational experience.
| Approach | Description | Benefits |
|---|---|---|
| Collaborative Group Work | Students work together to solve problems, share ideas, and discuss solutions. | Encourages teamwork, communication, and diverse problem-solving strategies. |
| Interactive Digital Tools | Using software or apps that allow students to visualize and manipulate concepts. | Offers visual learning and immediate feedback, which supports a deeper understanding. |
| Hands-On Activities | Physical tasks such as creating models or conducting experiments to explore concepts. | Provides tactile learning experiences and reinforces abstract ideas through action. |
| Peer Teaching | Students teach each other under the guidance of the instructor. | Promotes mastery through teaching, improves communication skills, and builds confidence. |
Incorporating these interactive approaches into the learning process creates a dynamic environment where students are more likely to engage with the material and retain knowledge. These strategies not only improve comprehension but also make learning more enjoyable and meaningful.
Resources for Additional Practice
Building proficiency in various concepts requires consistent practice and access to a variety of resources. By utilizing different tools and exercises, learners can reinforce their understanding and improve problem-solving abilities. There are numerous online platforms, workbooks, and interactive tools available that offer additional exercises tailored to help students master challenging topics.
These resources provide opportunities for extra practice, real-time feedback, and explanations to further clarify difficult concepts. Whether it’s through online tutorials, printable worksheets, or interactive games, supplementary resources can support continued learning and bolster confidence.
Online Platforms for Extra Practice
- Khan Academy: Offers free lessons and practice problems on a wide range of topics with step-by-step guidance.
- IXL Learning: Provides interactive exercises and personalized learning plans for continuous improvement.
- Prodigy: A game-based learning platform that adapts to students’ needs, providing engaging practice for various concepts.
- Cool Math Games: A fun, interactive site that provides math-based puzzles and challenges for students to practice their skills.
Printable Resources
- Teachers Pay Teachers: A marketplace offering printable worksheets, practice sets, and activities created by educators.
- Math Drills: Provides free printable worksheets covering a wide range of topics to practice independently.
- Education.com: Features worksheets, games, and activities that help students focus on specific learning objectives.
By exploring these resources, students can expand their practice opportunities, receive targeted feedback, and build a solid foundation for future lessons. Consistent use of these materials ensures that concepts are not only understood but also retained over time, contributing to long-term academic success.
Common Mistakes to Avoid
As students progress through learning complex concepts, it is easy to make certain errors that can hinder their understanding and lead to confusion. Being aware of these common pitfalls can help students avoid them and improve their overall performance. Recognizing these mistakes early allows learners to correct their approach and continue progressing with confidence.
Overlooking Instructions
One of the most frequent mistakes students make is failing to carefully read and follow the instructions. Skipping over important steps or not fully understanding the task can lead to incorrect results. It is crucial to take the time to thoroughly review what is being asked before attempting to solve a problem. Ensure that all instructions are followed and each part of the question is addressed.
Misinterpreting Problems
Another common error is misinterpreting the question or problem at hand. Whether it is misunderstanding a word problem or incorrectly identifying the operation to use, this can lead to major mistakes. Students should practice identifying key terms and details within each problem to ensure they are solving it correctly. Rereading the problem and breaking it down into smaller steps can help clarify its meaning.
Rushing Through Problems
Rushing through assignments or exercises can result in careless errors. It is important to approach each question thoughtfully, double-checking calculations and ensuring that every step is correct. Taking a moment to review the work before submitting it can prevent small but significant mistakes.
Avoiding these common mistakes can significantly improve the quality of work and ensure better understanding of the material. By developing careful reading habits, practicing patience, and double-checking work, students can build strong problem-solving skills and achieve greater success in their learning journey.
When to Seek Extra Help
Sometimes, despite best efforts, certain topics or concepts can remain challenging. It is important for students to recognize when they are struggling and seek additional assistance. Getting help at the right time can prevent frustration and keep students on track with their learning. Understanding when and how to ask for support is a key factor in achieving academic success.
Signs That Extra Help is Needed

- Repeated Struggles: If you find yourself repeatedly unable to solve similar problems or answer questions correctly, it might be time to seek guidance.
- Feeling Overwhelmed: When a particular topic or skill causes anxiety or makes you feel overwhelmed, it’s a sign that additional support might be beneficial.
- Lack of Understanding: If you’re not grasping the basic concepts despite studying or reviewing, this can indicate the need for outside help.
- Getting Poor Results: If your performance on quizzes, tests, or homework is consistently low, it may be time to address any gaps in understanding.
Where to Find Help
- Teachers: The first place to go for help is always your teacher. They can provide clarity on any areas of confusion and offer resources for further practice.
- Peer Tutoring: Sometimes working with a classmate or finding a peer tutor can help explain things in a different way.
- Online Resources: Many websites and online platforms offer tutorials, practice problems, and explanations for difficult concepts.
- Private Tutors: If you need more personalized instruction, consider working with a private tutor who can provide one-on-one support.
Seeking help when necessary can make all the difference in mastering challenging material. Don’t hesitate to ask for assistance – it’s an essential part of the learning process.