
In the journey of learning, students often encounter various challenges that require guidance and support. This section provides a comprehensive look at the strategies and approaches to help navigate through complex problems in the fourth-grade curriculum. It focuses on offering clarity and structured steps to reach the correct solutions, making learning more accessible and effective for young learners.
For both educators and parents, providing the right tools can significantly impact how students grasp key concepts and solve problems efficiently. This resource is designed to enhance understanding by breaking down tasks into manageable parts. By following these detailed solutions, learners can build confidence and improve their problem-solving abilities.
Through clear explanations and carefully worked-out examples, students are encouraged to approach each problem with a methodical mindset, ensuring they have the necessary skills for future learning. The goal is not only to provide answers but also to foster critical thinking and deeper comprehension.
Eureka Math Grade 4 Module 4 Answer Key
This section provides a detailed guide to solving the most common problems encountered in the fourth-grade curriculum. By reviewing and breaking down complex tasks, students can better understand the steps involved and develop the skills needed for problem-solving. This resource is meant to support learners in mastering critical concepts and improving their ability to work through challenging exercises with ease.
The focus is on giving learners the tools to independently tackle problems, reinforcing their understanding and boosting their confidence. With clearly explained solutions and a step-by-step approach, this guide helps both students and educators to navigate through key lessons. It’s not only about finding the right answers but also about strengthening the overall comprehension of essential principles.
Overview of Grade 4 Module 4
This section covers an essential part of the curriculum designed to strengthen students’ understanding of fundamental concepts and problem-solving techniques. The focus is on developing skills that are crucial for success in higher levels of learning, providing both a solid foundation and a deeper insight into key ideas. The exercises aim to challenge students while offering them the necessary tools to approach each task systematically.
In this unit, students are expected to work with a variety of topics that involve:
- Understanding complex numerical relationships
- Applying reasoning to solve practical problems
- Mastering the use of critical thinking techniques
- Exploring patterns and their applications
Each concept is introduced gradually, allowing students to build upon their knowledge and approach new challenges with confidence. The unit also encourages collaborative learning, helping students develop communication skills as they work together to explore new ideas.
By the end of this section, students should be equipped to apply what they’ve learned to both familiar and unfamiliar situations, using the concepts they’ve mastered to think critically and solve problems effectively.
Key Concepts in Module 4
This section highlights the critical topics and skills that students are expected to master. The concepts are designed to help learners develop a deeper understanding of relationships between numbers, enhance their ability to think analytically, and apply their knowledge in various problem-solving scenarios. The focus is on building a strong foundation that will be crucial for tackling more advanced concepts in future lessons.
Some of the essential ideas covered include:
- Operations with multi-digit numbers
- Understanding the relationships between different types of numbers
- Solving word problems with multiple steps
- Recognizing and using patterns to solve problems
- Developing strategies for efficient calculations
Each concept is carefully introduced and reinforced through a variety of examples, helping students grasp the underlying principles and see how they apply to real-world situations. The goal is to ensure learners can use these foundational skills confidently and effectively, both inside and outside the classroom.
Understanding the Problem-Solving Process

The ability to approach and solve problems is a crucial skill in learning. Understanding the steps involved in breaking down complex tasks into manageable parts is key to achieving success. This section focuses on providing a clear framework for students to follow when tackling challenging exercises, ensuring they can apply logical thinking and reasoning at each stage.
Effective problem-solving begins with understanding the problem itself. Once the issue is clear, students should focus on identifying relevant information and organizing their thoughts. Breaking down a problem into smaller steps allows learners to make progress in a structured way, avoiding confusion or frustration.
The process includes the following stages:
- Carefully reading the problem and identifying key information
- Choosing an appropriate method or strategy to approach the task
- Applying the chosen method and checking for consistency at each step
- Reviewing the final solution to ensure it makes sense
By practicing this method, students build confidence in their ability to handle complex problems independently, while also improving their critical thinking skills. This approach is not only effective in mathematics but is applicable across a wide range of academic disciplines and real-world situations.
Step-by-Step Solution Guide
This section provides a detailed, methodical approach to solving problems commonly encountered in the curriculum. The goal is to break down each task into clear, actionable steps, allowing learners to follow along with confidence. By focusing on a step-by-step process, students can approach even the most complex challenges in a structured manner, ensuring they understand each phase before moving forward.
Each solution begins with understanding the problem, followed by identifying the relevant information. The next step involves choosing the most appropriate strategy to solve the issue at hand, followed by executing the strategy with careful attention to detail. Finally, students review their work to ensure accuracy and consistency, checking for any errors or missed steps.
By adhering to this structured approach, learners can systematically work through problems, making it easier to grasp difficult concepts and strengthen their problem-solving abilities. This guide is designed to not only help with completing assignments but also to build critical thinking skills that will be valuable in a wide range of subjects and situations.
Common Challenges in Module 4
Throughout this section of the curriculum, students may encounter several challenges that require additional focus and understanding. These obstacles can range from grasping new concepts to applying strategies effectively. Addressing these issues early can help ensure that students build a strong foundation for more complex topics in the future.
Difficulty with Multi-Step Problems
One of the most common difficulties students face is working through multi-step problems. These exercises require learners to apply various skills in sequence, which can be overwhelming. Students often struggle to organize their thoughts and break down the problem into manageable steps. To overcome this, it’s important to practice step-by-step solutions, ensuring each part is understood before moving on to the next.
Understanding Abstract Concepts
Another challenge is understanding abstract concepts and how they relate to real-world situations. Some students find it hard to see the practical applications of certain ideas, making it difficult to retain and apply the information. To tackle this, students should focus on real-life examples that illustrate how the concepts are used in everyday life, helping to bridge the gap between theory and practice.
Patience and practice are essential in overcoming these challenges. By consistently reviewing the material, asking questions, and seeking clarification when needed, learners can successfully navigate through these obstacles and master the necessary skills.
How to Use the Answer Key Effectively
The goal of any solution guide is not just to provide the correct answers, but to help students understand the process behind each step. To use this resource effectively, it’s important to view it as a tool for learning, not just a shortcut to finding solutions. By analyzing the steps provided, learners can better grasp the underlying concepts and apply them to similar problems in the future.
Start by attempting each problem independently before referencing the solutions. Once you’ve made an attempt, compare your work with the provided steps. If there are discrepancies, review the solution carefully to identify where your approach diverged. Focus on understanding why a particular method or strategy was used, and think about how you can apply it to other problems.
Rather than relying solely on the answers, treat the guide as a learning aid to reinforce your understanding. This approach allows you to improve both your problem-solving skills and your overall comprehension of the subject. It’s important to ask yourself questions as you review the solutions, such as: “Why did this step make sense?” and “Could I have approached this differently?”
By using the solution guide in this way, students will not only solve the problems correctly but will also gain the confidence and skills needed for independent problem-solving in the future.
Tips for Parents and Teachers
Supporting students through their learning journey requires a collaborative approach between parents, teachers, and learners. By creating an environment where students feel encouraged to ask questions, explore different problem-solving strategies, and reflect on their progress, both parents and teachers can play a vital role in fostering a deeper understanding of key concepts. Here are some tips to help guide students toward success in their studies.
Creating a Supportive Learning Environment
Setting up a focused and positive learning space is crucial for effective study sessions. Here are some strategies to consider:
- Ensure the learning area is quiet and free from distractions.
- Provide all necessary materials, such as paper, pencils, and reference sheets.
- Establish a consistent study routine to help students stay on track.
- Encourage breaks to maintain focus and prevent frustration.
Guiding Through Challenges
When students encounter difficulties, it’s important to approach the situation calmly and with patience. Here are some tips to guide them effectively:
- Encourage students to read problems carefully and underline key information.
- Ask questions that prompt students to think critically about their approach.
- Help students break down complex tasks into smaller, manageable steps.
- Promote perseverance, reminding students that mistakes are part of learning.
By following these tips, both parents and teachers can help students build confidence, develop essential problem-solving skills, and create a strong foundation for future learning.
Learning Objectives for Module 4
In this section, students will focus on developing key skills and understanding essential concepts that will serve as building blocks for more advanced topics. The primary objectives aim to ensure students can apply learned strategies, approach problems systematically, and demonstrate mastery over the key concepts introduced. These objectives are designed to promote both comprehension and practical application of the skills.
Core Skills and Concepts
The following table outlines the main learning goals for this section, detailing the specific skills students should aim to develop and understand:
| Objective | Description |
|---|---|
| Problem Solving | Apply logical thinking to break down and solve complex problems step by step. |
| Conceptual Understanding | Gain a deep understanding of the core principles and their real-world applications. |
| Computation Techniques | Master various methods for solving arithmetic problems efficiently. |
| Critical Thinking | Enhance reasoning abilities by comparing different problem-solving approaches. |
Application and Mastery
To achieve these objectives, students should engage in hands-on practice, consistently applying the techniques learned to real-world scenarios. This will allow them to not only memorize procedures but also to internalize the logic behind each step. The goal is to build confidence and competence in both theoretical and practical aspects of the subject.
Strategies for Successful Practice
To achieve success in any learning area, consistent practice and the right approach are essential. The following strategies will help students build confidence, reinforce concepts, and improve problem-solving abilities. By focusing on the process and committing to regular practice, students can strengthen their skills and gain a deeper understanding of the material.
Effective Practice Techniques
Here are some strategies that can make practice sessions more productive and enjoyable:
- Start with the basics: Ensure a solid understanding of foundational concepts before moving on to more complex problems.
- Practice regularly: Consistency is key. Schedule short practice sessions throughout the week rather than cramming all at once.
- Work through examples: Go through examples step by step to understand the process behind each solution.
- Challenge yourself: Don’t be afraid to try more difficult problems once the basics are mastered. This will help expand skills and build confidence.
- Review mistakes: Analyze errors to understand where things went wrong. This is essential for learning and improving.
Developing a Positive Mindset
Creating a positive mindset is just as important as the actual practice. Encourage students to approach challenges with confidence, viewing mistakes as opportunities for growth. With the right attitude, practice becomes a tool for mastery rather than a task to be dreaded.
By following these strategies, students will not only improve their ability to solve problems but also build a stronger foundation for future learning.
How to Improve Skills in Grade 4
Developing strong skills in this stage of learning requires a combination of practice, understanding, and problem-solving techniques. The key to improvement lies in the ability to grasp core concepts and apply them consistently. By engaging in structured activities, reviewing material regularly, and tackling new challenges, students can gradually enhance their abilities and build confidence in their skills.
Building a Strong Foundation

The first step to improving is ensuring that students have a solid understanding of the foundational principles. This can be done by:
- Reviewing previous concepts: Reinforce skills from earlier lessons to ensure they form a strong base for new learning.
- Practicing regularly: Consistent practice is essential for strengthening abilities and boosting confidence.
- Focusing on one skill at a time: Trying to master one concept before moving on to the next ensures better retention and understanding.
Engaging in Practical Problem-Solving
Application is key to mastering any concept. To improve skills, students should regularly engage with real-world problems and challenge themselves to think critically. Here’s how to approach it:
- Solving problems from various sources: Practice with problems from different books, worksheets, or online resources to get a broad understanding.
- Breaking down complex tasks: Encourage students to break problems into smaller, manageable parts for easier solutions.
- Learning from mistakes: Help students see errors as learning opportunities, guiding them through corrections to deepen understanding.
By using these strategies, students can sharpen their skills and develop a more confident approach to solving challenges. Consistent practice, a positive mindset, and the ability to apply concepts effectively will go a long way in boosting overall performance.
Examples of Common Questions and Answers
When working through assignments, it’s common to encounter questions that require a deeper understanding of the material. These types of questions often test a student’s ability to apply concepts learned in class. Below are examples of frequently asked questions, along with their solutions, which will help clarify common challenges faced by students.
Example 1: Understanding Place Value
Question: What is the value of the digit 7 in the number 3,748?
Answer: The value of 7 in this number is 700, as it is in the hundreds place.
Example 2: Solving Word Problems
Question: If a student has 5 packs of stickers, and each pack contains 24 stickers, how many stickers does the student have in total?
Answer: To find the total number of stickers, multiply 5 (packs) by 24 (stickers per pack): 5 × 24 = 120 stickers.
These examples demonstrate how applying foundational skills to practical scenarios can lead to better problem-solving. Regular practice with similar types of questions can help reinforce concepts and increase confidence in tackling more complex challenges.
Reviewing Key Skills from Module 4
In this section, we will revisit some of the essential skills developed throughout the lessons. Mastery of these concepts is crucial for success, as they form the foundation for future learning. By reviewing key ideas and strategies, students can reinforce their understanding and become more proficient in solving problems. The following table summarizes the most important skills to focus on from this section.
| Skill | Description |
|---|---|
| Place Value Understanding | Recognizing the value of digits based on their position in a number, such as tens, hundreds, and thousands. |
| Multiplication and Division | Using multiplication and division strategies to solve problems involving equal groups and arrays. |
| Adding and Subtracting Fractions | Understanding how to add and subtract fractions with like denominators, as well as simplifying results. |
| Word Problems | Applying problem-solving skills to real-world scenarios by interpreting and solving word problems. |
By focusing on these skills, students can strengthen their problem-solving abilities and prepare for more advanced topics in the future. Regular practice and review are essential for retaining and applying these concepts effectively.
Support Materials for Module 4
To enhance learning and reinforce the skills covered, various resources can be used to provide additional support. These materials are designed to help students understand key concepts more clearly, provide practice opportunities, and offer alternative methods for tackling complex problems. The following resources can be invaluable for both students and educators alike:
- Practice Worksheets: Provide extra practice on key skills to ensure mastery of important concepts.
- Interactive Online Tools: Websites and applications that offer virtual exercises and games to engage students in hands-on learning.
- Video Tutorials: Step-by-step videos that explain various topics in a more visual and interactive way.
- Flashcards: Quick review tools to help reinforce vocabulary and concepts, ideal for memorization.
- Guided Notes: Pre-structured outlines to help students follow along and organize information during lessons.
These resources help to break down difficult concepts into more manageable parts and encourage active participation in the learning process. Utilizing such support materials alongside regular practice can significantly improve comprehension and retention of the material.
Exploring Additional Resources for Practice
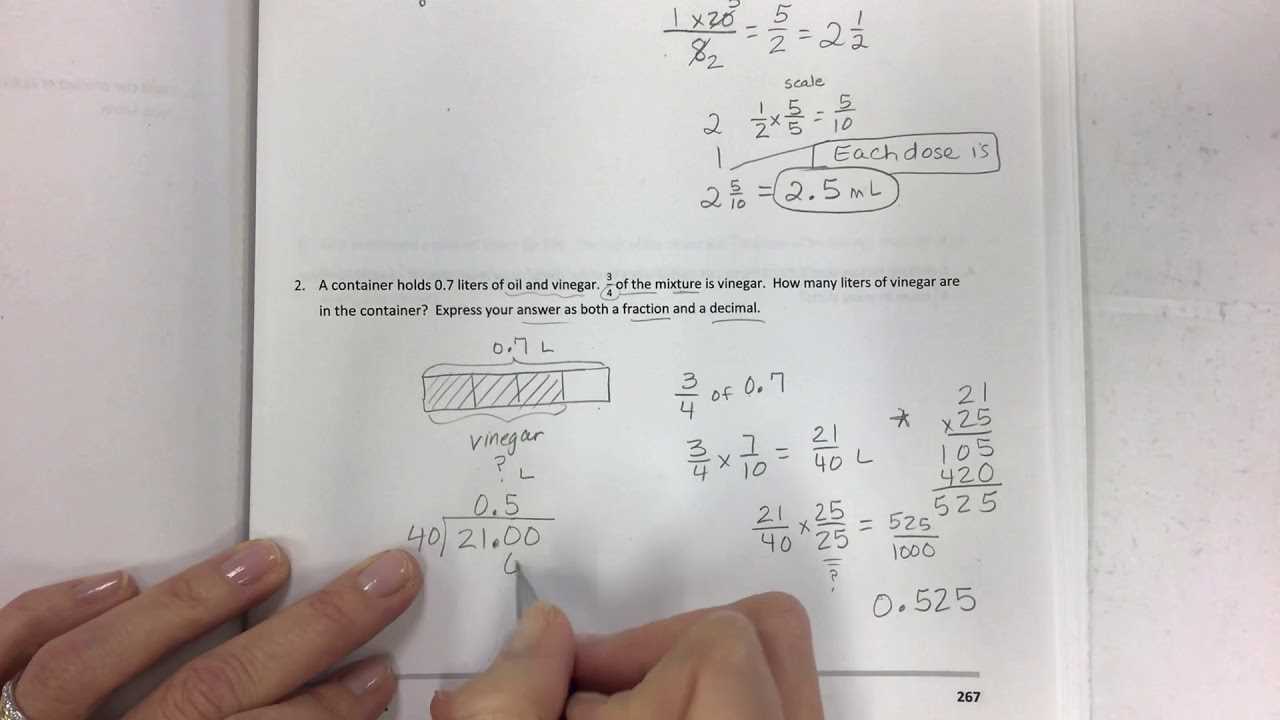
To further solidify understanding and gain mastery over key concepts, it is beneficial to explore a variety of supplementary resources. These materials provide opportunities for extra practice, ensuring that learners have the chance to strengthen their skills and boost confidence. Below are several effective resources designed to support continued learning and improvement.
Online Platforms and Tools
Several interactive platforms offer targeted exercises and challenges that help reinforce learning. These tools often include instant feedback, making them great for independent practice. Some of the most popular online resources include:
- Interactive Websites: Websites with custom quizzes and interactive lessons that adjust difficulty based on performance.
- Educational Apps: Mobile applications designed to support problem-solving and skill-building in a fun and engaging way.
- Online Games: Gamified learning experiences that make practicing skills enjoyable and interactive.
Printed Resources and Workbooks
Printed materials such as workbooks and exercise sheets remain highly effective for reinforcing learning. These resources allow learners to practice at their own pace without the need for electronic devices. Consider using:
- Practice Sheets: Worksheets that focus on specific topics, allowing for concentrated practice on challenging areas.
- Workbooks: Comprehensive resources that provide exercises, explanations, and step-by-step solutions to problems.
- Flashcards: Physical cards that help with quick recall of key facts, terms, or formulas.
Additional Practice Through Peer Interaction
Learning alongside others can be a highly effective way to enhance understanding. Collaborative learning environments, such as study groups or tutoring sessions, can provide diverse perspectives and helpful explanations.
| Resource | Type | Benefits |
|---|---|---|
| Interactive Websites | Online | Instant feedback, engaging challenges |
| Workbooks | Printed | Comprehensive, hands-on practice |
| Study Groups | Collaborative | Peer support, diverse explanations |
By combining different types of resources–whether digital tools, printed materials, or collaborative efforts–students can deepen their understanding and refine their skills in a variety of ways. Using multiple approaches ensures a well-rounded learning experience, ultimately leading to greater academic success.
Why Module 4 is Essential for Mastery
Understanding the foundational principles of problem-solving and number operations is crucial for building strong mathematical skills. The concepts covered in this section are designed to deepen a student’s ability to think logically, apply strategies to solve complex tasks, and foster critical thinking. Mastering these skills early on not only ensures success in future learning but also builds confidence in handling a variety of challenges.
Building a Strong Foundation for Future Concepts
The topics in this section are strategically selected to serve as the building blocks for more advanced concepts. By mastering these core ideas, students can more easily grasp higher-level topics in later stages. These fundamental skills, such as understanding relationships between numbers and solving multi-step problems, are frequently applied throughout the entire learning journey.
Enhancing Problem-Solving Skills
One of the most important skills that students develop in this section is problem-solving. This section encourages learners to approach tasks methodically, using step-by-step reasoning to break down complex problems. Through consistent practice, students learn how to identify patterns, recognize key information, and test solutions, all of which are essential for mastering more intricate subjects.
Ultimately, this section equips students with the tools they need not only to succeed in the immediate tasks but also to build a lifelong love of problem-solving and logical thinking. The ability to approach challenges confidently and systematically sets the stage for academic growth and real-world application.
Recommended Activities to Reinforce Learning
To solidify understanding and build confidence in tackling complex problems, it is essential to engage in hands-on practice that reinforces key concepts. Regular practice through a variety of activities not only enhances retention but also helps students gain fluency in applying learned strategies. Below are several activities designed to deepen comprehension and improve skills in tackling a range of challenges.
1. Practice Worksheets
Worksheets are an effective tool to practice specific skills and concepts. By completing exercises on their own, students can test their understanding and reinforce their problem-solving abilities. These worksheets can focus on key areas such as operations, number relationships, or word problems.
2. Group Problem-Solving Exercises
Working with others allows students to discuss different approaches to solving problems and learn from their peers. Group exercises are particularly helpful for developing collaboration and communication skills while reinforcing mathematical concepts.
3. Interactive Online Games
Online platforms often provide engaging and interactive games that focus on reinforcing key topics. These games can be a fun way to apply newly learned concepts and allow students to track their progress in a more dynamic way.
4. Visual Aids and Manipulatives
Using visual aids like number lines, charts, and manipulatives such as blocks or counters helps students visualize abstract concepts. These hands-on tools make it easier for learners to grasp the relationships between numbers and improve their problem-solving strategies.
5. Real-Life Application
Applying learned concepts to real-world scenarios is an effective way to make learning more meaningful. For example, students can be asked to calculate the total cost of a shopping list or determine the amount of ingredients needed for a recipe. These activities help students connect classroom learning to their everyday lives.
6. Review Games and Quizzes
Engaging students in review games and quizzes helps them consolidate their knowledge. Friendly competitions or timed quizzes provide a sense of urgency and challenge, making the review process more dynamic and enjoyable.
7. Reflection Journals

Encouraging students to reflect on what they’ve learned by writing about their experiences helps deepen their understanding. Keeping a learning journal where they summarize concepts or describe how they solved problems can aid in reinforcing key ideas.
Summary Table of Recommended Activities
| Activity Type | Description |
|---|---|
| Practice Worksheets | Worksheets with targeted problems for focused practice on specific skills. |
| Group Problem-Solving | Collaborative exercises to develop teamwork and problem-solving strategies. |
| Interactive Online Games | Engaging digital games to practice learned concepts in a fun environment. |
| Visual Aids | Using charts, number lines, and manipulatives to visualize abstract concepts. |
| Real-Life Application | Practical exercises that apply learning to everyday scenarios. |
| Review Games | Interactive review games and quizzes for reinforcing key ideas. |
| Reflection Journals | Writing reflections on learning to deepen understanding and retention. |
These activities not only help reinforce the material but also encourage a deeper understanding of the concepts. Consistent practice through varied approaches ensures students gain both proficiency and confidence in their skills.
Final Thoughts on Grade 4 Math Success
Achieving success in learning complex concepts requires more than just completing assignments. It involves continuous engagement, practice, and a positive mindset. As students progress through various topics, they build a foundation of skills that not only help them master the current content but also prepare them for future challenges. Here are some key takeaways to ensure long-term success in mathematical learning:
- Consistency is Key: Regular practice, even in small increments, solidifies the understanding of new concepts. The more a student practices, the more confident they become in their abilities.
- Understand, Don’t Memorize: A deep understanding of the concepts ensures that students can apply their knowledge to different scenarios. Rather than relying on rote memorization, students should aim to grasp the underlying principles that guide problem-solving.
- Stay Positive and Patient: Learning takes time, and it’s important to approach challenges with patience. When students encounter difficulties, it’s crucial to provide encouragement and foster a growth mindset, where challenges are seen as opportunities for growth.
- Utilize a Variety of Resources: There are numerous resources available, from online tools to hands-on manipulatives. Using a combination of these can help students engage with the material in different ways and reinforce their understanding.
- Collaborate and Communicate: Learning in groups or discussing problems with others can offer new perspectives and strengthen problem-solving strategies. Communication and teamwork are invaluable skills that contribute to academic and personal growth.
Ultimately, the key to mastering any subject is persistence, practice, and support. By maintaining a steady routine, staying engaged with the material, and seeking help when necessary, students can overcome obstacles and achieve success in their learning journey.