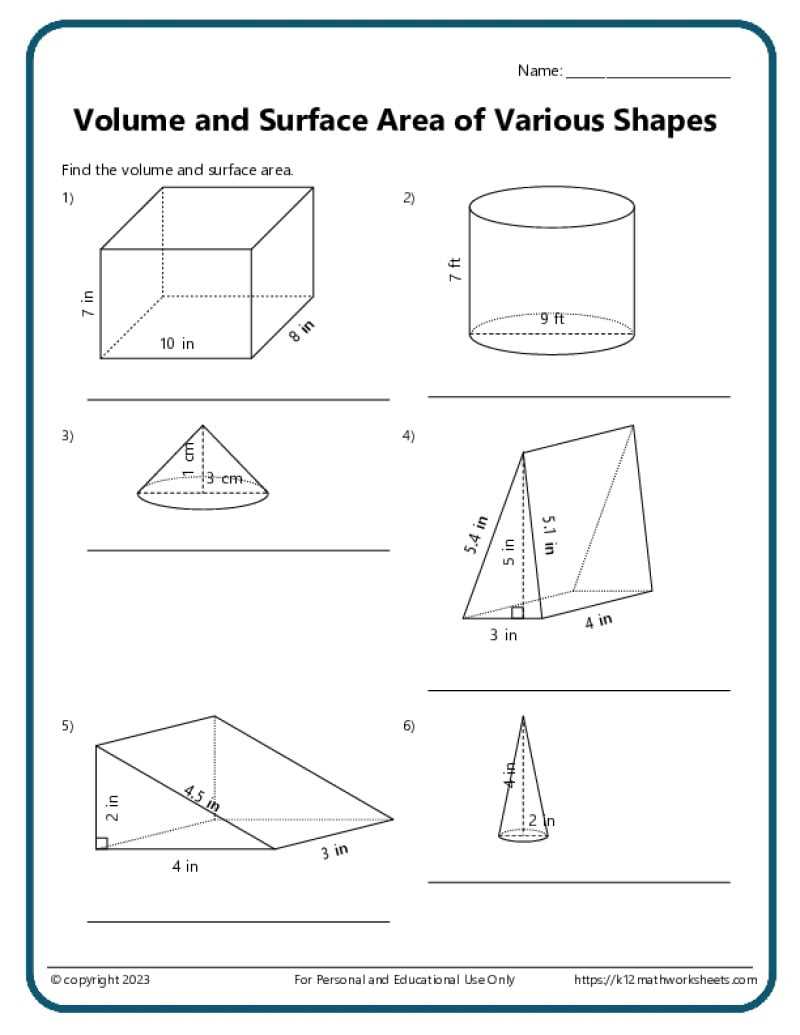
In geometry, the calculation of physical properties of objects plays a crucial role in understanding their structure. These calculations help in determining the extent of an object’s exterior or the space it occupies, which is vital in various fields like engineering, design, and architecture. The process involves applying specific formulas to derive these measurements, depending on the shape and dimensions of the object in question.
Whether you are working with simple shapes such as cubes and spheres, or more complex forms, mastering these techniques is essential for accurate problem-solving. Knowing how to efficiently determine these values is not only important for academic purposes but also for practical applications in real-world scenarios. Proper understanding of these concepts allows for precise calculations in tasks ranging from construction to packaging design.
By breaking down these formulas and their usage, anyone can improve their ability to solve related problems quickly and effectively. This guide will assist in clarifying the steps involved, providing clear examples, and offering helpful insights into tackling common challenges with geometric calculations.
Surface Area and Volume Answer Key Guide
Understanding how to calculate the extent of an object’s exterior or the space it occupies is fundamental in geometry. This guide will help clarify the essential formulas and techniques needed to solve these types of problems. Whether you’re dealing with basic or complex shapes, having a structured approach to the calculations makes the process much more manageable and accurate.
To begin, it’s important to identify the correct formula for the object in question. Each shape has its own specific method for determining the relevant measurement. Here is a breakdown of some of the most common forms and the essential equations for their evaluation:
- Cuboid: To find the exterior extent, multiply the length, width, and height.
- Sphere: Use the radius to calculate the extent or the space inside.
- Cylinder: Combine the radius and height for precise results.
- Cone: Requires the base radius and height for an accurate determination.
Once the correct formula is selected, applying the right measurements will yield the desired result. However, to avoid common mistakes, it’s crucial to remember a few key principles:
- Ensure that all dimensions are in the same unit of measurement before applying the formula.
- Double-check the values used for the radius or height to avoid miscalculations.
- Pay attention to the units of the final result to ensure consistency and correctness.
By following these steps, anyone can confidently perform calculations for a wide range of objects. With practice, the process becomes faster and more intuitive, making it easier to tackle even the most complex geometric challenges.
Understanding Surface Area Formulas
Calculating the extent of an object’s outermost parts requires a solid understanding of the formulas used for different shapes. Each shape has specific characteristics, and knowing the right approach helps to determine the outer dimensions efficiently. These formulas help solve real-world problems by providing precise measurements needed in fields like construction, packaging, and engineering.
For regular shapes, such as cubes, spheres, and pyramids, the formulas are straightforward and rely on simple measurements like length, width, height, or radius. For irregular objects, the process may involve more advanced techniques, but the concept remains the same: break down the shape into manageable parts and apply the correct formula to each.
Here are some of the most commonly used formulas to calculate the exterior of common geometric shapes:
- Cube: Multiply the length of one side by itself and then multiply by six (since all sides are equal).
- Rectangular Prism: Add up the areas of all six faces, using the formula 2(lw + lh + wh), where l = length, w = width, h = height.
- Cylinder: Use the formula 2πr² + 2πrh, where r is the radius and h is the height.
- Sphere: The formula is 4πr², where r is the radius.
- Pyramid: The calculation involves adding the base area to the area of the triangular faces. The formula is base area + ½ x perimeter x slant height.
Understanding these formulas and knowing when to apply them is crucial for accurate calculations. With practice, anyone can become proficient in determining these measurements, ensuring precise results for various practical applications.
How to Calculate Volume of Solids
Determining the amount of space occupied by a three-dimensional object is an essential skill in geometry. The process involves applying specific formulas based on the shape of the object. Each solid has a unique method to find how much space it fills, and understanding these methods is key to accurate calculations.
For regular shapes like cubes, cylinders, or spheres, the formulas are simple and rely on basic measurements such as length, radius, or height. For irregular solids, the approach may be more complex, often requiring approximation or the use of more advanced techniques. Here’s a guide on how to calculate the space inside various solids:
- Cube: Multiply the length of one side by itself three times (side³).
- Rectangular Prism: Multiply length, width, and height (l × w × h).
- Cylinder: Use the formula πr²h, where r is the radius and h is the height.
- Sphere: The formula is (4/3)πr³, with r representing the radius.
- Cone: Multiply the base area by the height and divide by three (1/3 × πr²h).
These formulas are the foundation for calculating the space inside solids. Once the appropriate formula is chosen, simply substitute the known values and perform the necessary arithmetic to find the result. It’s essential to ensure that all measurements are in the same unit before performing the calculations to maintain accuracy.
Key Concepts in Surface Area Calculation
Understanding the method to determine the outer dimensions of a three-dimensional object is essential in geometry. It involves calculating the total measurement of all the exterior faces that enclose the shape. The process varies depending on the type of object, but all calculations follow a similar approach: identify the individual faces and apply the correct formulas for each. Once you know the methods, it becomes straightforward to find the total external measurement.
Basic Principles of Calculation
When calculating the external measurement of a solid, it’s important to keep a few core principles in mind:
- Identifying the faces: Every shape has distinct faces that need to be measured. For instance, a cube has six square faces, while a cylinder has two circular faces and one rectangular face.
- Formula selection: Each shape requires a specific equation. The correct formula depends on the shape’s dimensions, like length, width, height, or radius.
- Units of measurement: Ensure that all dimensions are in the same unit before performing the calculations to ensure consistency in the results.
Common Shapes and Their Formulas
Here are some of the most common shapes and their formulas for calculating the external measurement:
- Rectangular Prism: Multiply the length, width, and height of the shape, then sum the areas of all six faces.
- Cube: Since all sides are equal, simply calculate one side’s square and multiply by six.
- Cylinder: Add the area of the two circular faces (πr²) and the area of the side (2πrh).
- Sphere: The formula involves 4πr², where r is the radius of the shape.
Mastering these concepts and knowing how to apply the right formulas will greatly improve your ability to solve problems involving the measurement of objects’ exteriors, whether in mathematics or real-world applications.
Common Mistakes in Volume Problems
When working with three-dimensional shapes, it’s easy to make errors in calculations that can lead to incorrect results. These mistakes often stem from misunderstanding the formulas, incorrect measurements, or failing to apply the right units. Recognizing these common pitfalls can help avoid frustration and improve accuracy in problem-solving.
Frequent Errors to Avoid
Some of the most common mistakes in determining the amount of space inside a solid include:
- Incorrect formula application: Using the wrong equation for the shape in question can lead to significant errors. Each solid has its own distinct method for calculating the internal space, so double-checking the formula is essential.
- Mixing up dimensions: Confusing length with height, or radius with diameter, can result in inaccurate results. Always ensure you are using the correct measurements for the given shape.
- Unit inconsistencies: Using different units (e.g., inches for radius and centimeters for height) can cause discrepancies. Always convert all units to the same system before performing calculations.
Examples of Incorrect Calculations
Here’s a table showcasing some common mistakes and the correct approach for certain solids:
| Shape | Common Mistake | Correct Formula |
|---|---|---|
| Cylinder | Using the area of the base instead of multiplying by the height | πr²h |
| Sphere | Using 2πr² instead of 4πr³ | (4/3)πr³ |
| Rectangular Prism | Adding length, width, and height instead of multiplying | l × w × h |
Being aware of these mistakes and correcting them will help improve the precision of your calculations. Whether you’re working on homework, a project, or a real-world application, attention to detail is crucial for achieving accurate results.
Examples of Surface Area Equations
Calculating the total exterior measurement of various three-dimensional shapes involves using specific formulas based on the geometry of the object. Each shape has a distinct method for finding its overall extent, and understanding these equations is essential for accurate results. Below are some examples of common solids, their respective equations, and how to apply them for precise calculations.
For basic shapes like cubes, cylinders, and spheres, the formulas are straightforward, involving simple multiplication or addition of known measurements such as length, radius, or height. For more complex objects, the process may involve breaking the shape into parts and calculating the individual measurements for each face. Here are some key equations:
- Cube: Since all sides are equal, the equation is 6 × side².
- Rectangular Prism: Add the areas of all six faces using the formula 2(lw + lh + wh), where l = length, w = width, h = height.
- Cylinder: The total measurement is found by adding the areas of the two circular faces and the lateral side. The formula is 2πr² + 2πrh, where r is the radius and h is the height.
- Sphere: The formula for a sphere is 4πr², where r is the radius of the sphere.
- Pyramid: To calculate the exterior, use the formula base area + (½ × perimeter × slant height).
These equations allow for accurate calculation of the outer dimensions of many common shapes. Once the correct formula is identified, it’s important to apply the right measurements and units to ensure precision. Understanding the relationships between the different parts of the object will help in making accurate calculations for practical use.
Volume Formulas for Different Shapes

Calculating the amount of space occupied by various three-dimensional objects requires different approaches depending on the shape. The method for determining how much a solid holds relies on specific mathematical formulas that consider the unique properties of each figure. Understanding these formulas allows for accurate space calculations for a wide range of objects, from simple cubes to complex pyramids and spheres.
Common Formulas for Regular Shapes

Here are some of the most widely used formulas for calculating the internal space of different solids:
- Cube: The formula is side³, where the side refers to the length of one edge of the cube.
- Rectangular Prism: Multiply the length, width, and height (l × w × h) to determine the internal capacity.
- Cylinder: The formula is πr²h, where r is the radius of the base and h is the height of the cylinder.
- Sphere: The internal space of a sphere is calculated using (4/3)πr³, where r is the radius of the sphere.
- Cone: The formula is (1/3)πr²h, where r is the radius of the base and h is the height of the cone.
Formulas for Irregular and Complex Shapes
For more complex or irregular objects, determining internal space may involve breaking the shape into smaller, more manageable parts. In such cases, the process might involve adding or subtracting the spaces of individual sections. Examples of complex shapes might include pyramids, frustums, or irregular polyhedrons, which require specific adaptations of the basic formulas to calculate their internal measurements accurately.
- Pyramid: The formula is (1/3) × base area × height. The base area depends on the shape of the pyramid’s base.
- Frustum of a Cone: The formula is (1/3)πh(r₁² + r₁r₂ + r₂²), where r₁ and r₂ are the radii of the two circular ends, and h is the height.
Knowing how to apply these formulas and adjust for different shapes helps ensure accurate calculations when working with three-dimensional objects. With practice, determining the internal space of any solid becomes a straightforward task.
Applying Surface Area in Real Life
Understanding how to calculate the total exterior measurement of objects is not only important in math but also plays a crucial role in real-world applications. From construction to manufacturing, the ability to calculate the size of the outer boundary of a shape is essential for practical purposes, such as determining material requirements, coating coverage, and even environmental impact. By applying these concepts, professionals in various fields can make more informed decisions and optimize processes.
In everyday life, these calculations are used to solve problems related to packaging, painting, construction, and more. Whether you’re wrapping a gift, building a structure, or creating a design, knowing how much material is needed can save time and resources. Below are some common examples of how these calculations are applied:
- Painting Walls: When painting a room, it’s essential to calculate the total external measurements of the walls to determine how much paint is required. This helps avoid waste and ensures enough coverage.
- Building Construction: In construction, understanding the outer dimensions of materials like bricks, wood panels, and steel plates allows for accurate planning and material estimation, reducing costs and increasing efficiency.
- Packaging: Manufacturers often need to calculate the outer boundary of products or containers to determine the amount of wrapping or packaging material required. This is especially important in industries like food packaging or shipping.
- Solar Panels: In the energy sector, the total exterior measurement of solar panels is calculated to estimate the amount of sunlight they can absorb, helping to design more efficient energy systems.
By applying these principles in practical scenarios, individuals and businesses can optimize their operations, reduce costs, and make more informed choices in product design and material usage. Understanding the real-life applications of these calculations highlights the value of geometry beyond the classroom.
Volume Calculation in Engineering
In engineering, determining the amount of space occupied by various structures, materials, or fluids is a fundamental task. These calculations are essential for designing efficient systems, ensuring safety, and optimizing resources. Engineers use mathematical models to compute the internal capacity of different objects, whether in construction, manufacturing, or fluid dynamics. Accurately calculating the internal measurements is crucial for material estimation, structural integrity, and functional performance of designs.
From determining the capacity of tanks to calculating the load-bearing capacity of beams, understanding internal space is key in many engineering fields. It affects the design of infrastructure, machinery, and even electronics. Below are several areas where this calculation plays a significant role:
- Civil Engineering: In construction, calculating the internal capacity of beams, columns, and foundations helps engineers design structures that can safely support weight and withstand external forces.
- Mechanical Engineering: Calculating the space inside mechanical parts, such as engines, pistons, and pipes, ensures that components fit together properly and function efficiently. This is also crucial in fluid dynamics and heat transfer calculations.
- Aerospace Engineering: Engineers in this field need to calculate the internal space of aircraft and spacecraft to optimize fuel capacity, payload weight, and structural design, ensuring maximum performance and safety.
- Environmental Engineering: Accurate calculations are essential for designing systems that manage natural resources. For example, determining the capacity of water treatment tanks or waste storage facilities ensures proper operation and regulatory compliance.
By using the appropriate formulas for different shapes and structures, engineers can optimize designs, enhance safety, and improve the efficiency of systems across various industries. Volume calculations are an essential tool in achieving practical and effective engineering solutions.
Units Used in Surface Area Calculations

When determining the external measurement of different shapes, the correct units are essential for accurate results. These units help quantify the size of an object’s outer boundary, whether in small-scale projects or large engineering designs. The choice of units depends on the size of the object and the context of the calculation. Using appropriate units ensures consistency and clarity in reporting the results, making them applicable in real-world applications.
Common Units for Measurement
The most common units for measuring the external dimensions of objects include:
- Square Millimeters (mm²): Typically used for small objects or measurements in fields like jewelry design or precision engineering.
- Square Centimeters (cm²): Often used in everyday situations, such as measuring small household items or architectural models.
- Square Meters (m²): Commonly used in construction, landscaping, and interior design for larger spaces or areas, such as floors and walls.
- Square Inches (in²): Used primarily in the United States for small to medium-scale projects, such as in manufacturing or packaging.
- Square Feet (ft²): Widely used for measuring floor space or large areas, particularly in real estate or construction projects.
- Square Yards (yd²): Sometimes used in landscaping or construction, particularly for large plots of land.
Conversions Between Units
When working across different measurement systems, it’s often necessary to convert between units to ensure consistency. For instance, converting from square inches to square feet or from square meters to square yards is important in international projects or where different standards are used. The conversion formulas are straightforward:
- 1 square meter = 10,000 square centimeters
- 1 square foot = 144 square inches
- 1 square yard = 9 square feet
Having a solid understanding of these units and their conversions is essential for accurate calculations and effective communication in various fields, from engineering to interior design.
How to Use Pi in Volume Formulas
Pi is a mathematical constant that plays a crucial role in calculating the internal capacity of circular or cylindrical objects. This number, approximately equal to 3.14159, is essential for accurately determining the space enclosed by circular or spherical shapes. Understanding how to apply pi in calculations ensures precision, whether designing mechanical parts, determining storage capacities, or solving problems in engineering and architecture.
In many geometric shapes, the use of pi is directly related to their circular or curved components. For example, in spheres, cones, and cylinders, pi is used to account for the curvature and the circular cross-sections of these objects. Here’s how it fits into common formulas:
- Cylinder: To calculate the capacity of a cylinder, the formula is π × r² × h, where r is the radius of the base and h is the height.
- Sphere: The internal space of a sphere is determined using 4/3 × π × r³, where r represents the radius.
- Cone: A cone’s internal capacity is calculated with the formula 1/3 × π × r² × h, with r being the radius and h the height.
By applying pi in these formulas, you can accurately determine the amount of space an object occupies. This is essential for practical tasks, such as determining the amount of liquid a container can hold, the amount of material needed to construct a hollow object, or even the fuel capacity of cylindrical tanks.
Mastering the use of pi in these calculations is an important skill for anyone working with geometrically complex shapes, ensuring precise measurements and efficient design.
Surface Area and Volume in Geometry
In the study of shapes and their properties, understanding how to calculate the outer dimensions and internal capacity of objects is fundamental. These measurements allow for practical applications in various fields such as architecture, engineering, and design. The ability to compute the extent of an object’s boundary or the amount of space it contains is essential when working with both simple and complex geometric forms.
Geometric Shapes and Their Properties
Various geometric figures have specific formulas for determining their boundary extent and internal content. These formulas depend on the type of shape being analyzed. For example, spherical objects require a different approach compared to rectangular prisms or pyramids. Here are some common shapes and their related calculations:
- Cylinder: A three-dimensional object with two circular bases. The formula for calculating its boundary involves the radius of the base and height.
- Sphere: A perfectly round object where calculations depend solely on the radius.
- Rectangular Prism: A solid with six rectangular faces, where calculations involve the length, width, and height.
- Pyramid: A shape with a polygonal base and triangular sides, where formulas are derived from the base area and height.
Importance of Accurate Calculation
Accurate measurements of these properties are crucial in fields that involve construction, manufacturing, and scientific research. Whether calculating the amount of material required for a project or determining the capacity of a container, precise formulas are needed to ensure correctness. In addition, geometric understanding allows for efficient optimization of space, material usage, and overall design.
Mastery of these fundamental calculations not only enhances practical problem-solving but also deepens the appreciation of geometry’s role in shaping the physical world.
Comparing Surface Area and Volume
When analyzing geometric objects, two key concepts emerge: the measurement of the object’s external extent and the measurement of the space it holds. Although both involve understanding the properties of a shape, they focus on different aspects. The first looks at the boundaries or exterior, while the second focuses on the interior or the capacity within the shape. These two measurements are essential for various real-world applications, from packaging to architecture.
Key Differences Between External Extent and Internal Capacity
While both calculations are integral to understanding a shape’s characteristics, they are used in different contexts. External measurements are often employed when determining the materials needed for the construction of an object or surface coverage, whereas internal measurements are crucial for understanding the capacity or the amount of space an object can hold.
| Aspect | External Extent (Boundary) | Internal Capacity |
|---|---|---|
| Focus | Object’s boundary or exterior | Space contained within the object |
| Application | Material calculation, surface treatment | Storage, content calculation |
| Measurement Units | Square units (e.g., cm², m²) | Cubic units (e.g., cm³, m³) |
| Formula Examples | π × r² × h (cylinder), 2lw + 2lh + 2wh (rectangular prism) | π × r² × h (cylinder), 1/3 × π × r² × h (cone) |
Applications in Real-World Scenarios
Both measurements serve vital functions in different industries. For instance, in packaging design, knowing the external extent helps optimize material usage, while the internal capacity determines how much can be stored or transported. In architecture, understanding the external extent ensures appropriate use of surface finishes, while internal measurements are crucial for creating usable, functional spaces.
By comparing the differences in focus, application, and measurement units, it’s clear that both concepts are intertwined, yet each serves a distinct purpose in the analysis of geometric shapes.
3D Shapes and Their Surface Areas
Understanding the external characteristics of three-dimensional objects is crucial in various fields, including design, construction, and manufacturing. The measurement of the external dimensions of these shapes helps in determining how much material is required for coverings, coatings, or packaging. Each shape has a unique way of calculating its external extent, depending on its structure and the number of faces or boundaries it has.
Common 3D Shapes
Three-dimensional shapes come in various forms, each with distinct properties that define their external dimensions. Below are some common examples:
- Cube: A shape with six equal square faces.
- Rectangular Prism: A shape with six rectangular faces, where opposite faces are equal.
- Cylinder: A shape with two circular faces and a curved side connecting them.
- Sphere: A perfectly round shape with no edges or corners.
- Pyramid: A shape with a polygonal base and triangular sides meeting at a single point.
- Cone: A shape with a circular base and a pointed top.
Calculating External Dimensions
Each three-dimensional shape has a specific formula for calculating its external measurement. Below are some formulas for the common 3D shapes:
- Cube: 6 × (side length)²
- Rectangular Prism: 2lw + 2lh + 2wh (where l = length, w = width, h = height)
- Cylinder: 2πr² + 2πrh (where r = radius, h = height)
- Sphere: 4πr² (where r = radius)
- Pyramid: Base area + (1/2 × perimeter of base × slant height)
- Cone: πr² + πr × slant height
These formulas help in determining how much material is required for covering or wrapping the shape, ensuring accurate estimations for construction, design, or packaging projects.
Calculating Volume for Irregular Objects
When dealing with objects that do not have a uniform or simple shape, calculating their internal capacity can be more challenging. These irregular forms require specific methods and techniques to determine how much space they occupy. Unlike regular geometric shapes, which have straightforward formulas, irregular objects often need creative approaches to estimate their size accurately.
Methods for Determining the Capacity
There are several techniques available for calculating the internal capacity of irregular objects. The choice of method often depends on the object’s characteristics and the level of precision required.
- Water Displacement Method: One of the simplest ways to find the internal capacity of an object is by immersing it in a liquid and measuring the volume of displaced liquid. This is commonly used for objects that can be fully submerged.
- Approximation with Regular Shapes: In some cases, irregular objects can be approximated by breaking them down into smaller, regular shapes. The total internal space can then be calculated by finding the sum of the capacities of the individual shapes.
- 3D Scanning and Modeling: Advanced technology allows for the creation of a 3D model of the object, where volume can be calculated based on digital representations.
Example of Water Displacement Method
Let’s consider an example using the water displacement technique:
| Step | Action | Measurement |
|---|---|---|
| 1 | Fill a container with water | Volume of water before immersion |
| 2 | Submerge the object | Volume of water after immersion |
| 3 | Calculate the difference | Difference = Volume of displaced water (object’s internal capacity) |
This method can be especially useful when dealing with irregularly shaped items such as rocks, sculptures, or objects with intricate details. By using the water displacement technique, an accurate estimate of the internal capacity can be easily obtained without complex calculations.
Surface Area and Volume in Physics
In the field of physics, the concept of space occupied by an object plays a critical role in understanding various principles and phenomena. Whether it’s calculating forces, heat transfer, or fluid dynamics, knowing how much space an object occupies and how its outer boundaries interact with the surrounding environment is essential for accurate predictions and analyses. These quantities are often used to explain physical behavior in different contexts, ranging from simple mechanics to complex thermodynamics.
Role in Heat Transfer
One of the most common applications of these calculations in physics is in the study of heat transfer. The rate at which heat flows into or out of an object depends on how much contact the object has with its surroundings, which can be quantified by its external dimensions. A larger exposed area allows for more heat exchange, which is crucial in fields like engineering, climate science, and materials science.
- Example: A metal plate with a greater surface in contact with the air will absorb or release heat faster than a smaller one, even if they are the same material and temperature.
- Application: This principle is applied in the design of radiators, cooling systems, and even the surface coatings used in spacecrafts to regulate temperature during re-entry.
Fluid Dynamics and Object Movement
In fluid dynamics, the amount of space an object takes up and its outer shape significantly influence how it moves through a fluid. Whether it’s the drag on an airplane wing or the buoyancy of a submerged object, these calculations determine the forces acting on the object, which in turn affect its speed, stability, and overall performance.
- Example: A streamlined object with a smaller cross-sectional profile encounters less resistance in the air compared to a similarly sized object with a larger surface.
- Application: This concept is vital in aerodynamics, the design of underwater vehicles, and even predicting the motion of objects in fluids like water or air.
By understanding how the occupied space and exposed boundaries of an object affect the forces and interactions in different physical systems, we can make more informed decisions in design, experimentation, and the advancement of technology. From the microscopic to the macroscopic scale, these concepts are integral to modern physics.
Tips for Solving Surface Area Problems
When approaching problems that involve the measurement of the outer boundaries of an object, there are several strategies to simplify the process. Understanding the principles behind these calculations is key to tackling complex shapes and ensuring accuracy. By breaking down the steps and applying consistent methods, you can efficiently solve problems that might otherwise seem daunting.
1. Identify the Shape
The first step is to carefully identify the geometry of the object. Different shapes have specific formulas that apply only to them. Recognizing whether the object is a sphere, cylinder, cube, or any other type will guide you to the correct approach. Familiarize yourself with the formulas associated with each type, as they will save you time and effort during calculations.
2. Break the Object Into Simple Parts
Many objects are combinations of simpler shapes. For example, a complex shape might consist of a cylinder with attached cones or spheres. By breaking the object into smaller, more manageable sections, you can calculate the measurements for each piece separately, then combine them for the final result.
- For a cylindrical object, calculate the sides first, then address the top and bottom.
- For more irregular shapes, separate the components and treat each as an individual entity before combining their results.
3. Check Units and Conversion
Ensure that all units are consistent throughout the calculation. Often, the measurements provided may be in different units, such as meters, centimeters, or inches. Converting all dimensions to the same unit before proceeding is crucial for accuracy. This prevents errors and ensures that your final result is in the desired unit of measurement.
4. Use the Correct Formula
Using the right equation is essential. Make sure you know the formula specific to the shape in question. For example, the formula for a sphere’s external boundaries differs from that of a cube or cone. Verify the formula with reliable sources or reference materials before beginning the calculation.
5. Double-Check for Symmetry
In some cases, symmetry can simplify the process. For symmetrical shapes, you can calculate one part and multiply by the number of symmetrical parts. This reduces the amount of work involved and helps to avoid calculation errors.
By following these tips, you can approach problems involving the measurement of outer dimensions with confidence. Consistent practice and attention to detail will make these types of calculations more intuitive over time.