
Mathematics can often be challenging, especially when it comes to grasping complex concepts and solving intricate problems. The process of learning is significantly enhanced when students have access to detailed explanations and solutions that help break down difficult topics. By providing comprehensive resources, learners can navigate through the different stages of mastering mathematical theories and problem-solving techniques.
In any mathematical curriculum, having reliable tools to verify and understand solutions is essential for progress. These resources not only allow students to check their work but also give them the opportunity to explore alternative methods of reaching the correct outcomes. Such tools serve as valuable assets in reinforcing understanding and boosting confidence in tackling new challenges.
With the right support materials, students can strengthen their grasp of mathematical concepts, improve their critical thinking skills, and become more adept at solving problems efficiently. These resources are not only beneficial for immediate assignments but also serve as stepping stones for future mathematical success.
Core Connections Algebra Answer Key
Access to a reliable guide for solving mathematical problems is crucial for students aiming to understand complex concepts and refine their skills. These guides provide the necessary resources to check solutions, explore different solving methods, and clarify doubts encountered during practice. They act as supportive tools for students, ensuring they stay on track with their learning progress.
Benefits of Using a Solution Guide

Utilizing a detailed solution guide allows learners to see step-by-step breakdowns of problems, making it easier to understand the thought process behind each solution. It enhances comprehension and helps identify any mistakes in their approach. By reviewing each solution carefully, students can develop a deeper understanding of mathematical principles and apply them to future problems.
Improving Problem-Solving Skills
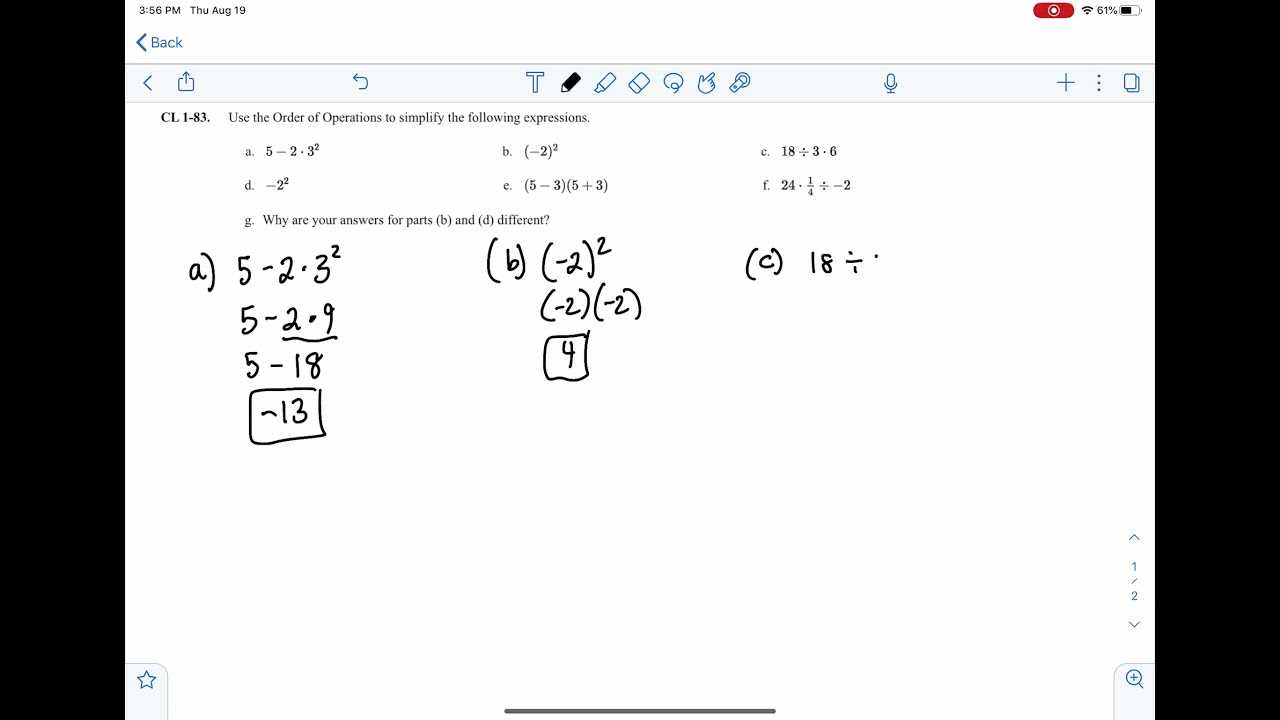
With the right resources, students can sharpen their problem-solving abilities by exploring various solving techniques. These guides serve as valuable tools for self-assessment, providing instant feedback that fosters better decision-making and logical thinking. They not only help in solving immediate exercises but also prepare students for more advanced topics in mathematics.
Understanding Core Connections Algebra
Grasping the fundamentals of mathematical concepts is essential for mastering more advanced topics. A strong foundation allows students to approach problems with confidence and develop the critical thinking skills necessary for solving increasingly complex tasks. This approach not only simplifies understanding but also makes learning more engaging and less intimidating.
The process of learning mathematics involves breaking down abstract concepts into smaller, manageable steps. By providing clear explanations and multiple examples, students can build their knowledge gradually, ensuring they understand each step before moving on. These methods allow learners to recognize patterns, improve their reasoning abilities, and connect new knowledge to existing skills.
How the Answer Key Helps Students
Having access to a comprehensive guide to verify solutions can significantly enhance a student’s learning experience. It provides a means to check their work, identify any mistakes, and understand the proper methods for solving problems. This tool is especially useful in building confidence, ensuring that students not only get the right answers but also learn the underlying processes involved in reaching those answers.
Building Confidence and Understanding
By using a solution guide, students can double-check their results and gain a clearer understanding of where they went wrong if their solution was incorrect. This immediate feedback is valuable for reinforcing learning, as it helps students comprehend the logic behind each step and improve their approach to similar problems in the future.
Supporting Independent Learning
One of the main benefits of a solution guide is that it encourages independent learning. Students can solve problems on their own and then refer to the guide for verification, making them more self-reliant. This autonomy helps cultivate problem-solving skills, critical thinking, and a deeper understanding of the subject matter.
Key Features of the Algebra Curriculum

The structure of a mathematics curriculum is designed to guide students through progressively challenging concepts while reinforcing previously learned material. A well-developed program focuses on building a strong foundation in mathematical reasoning, critical thinking, and problem-solving skills. It ensures that learners can apply their knowledge in practical situations and gain the confidence needed to tackle complex tasks.
Comprehensive Concept Development
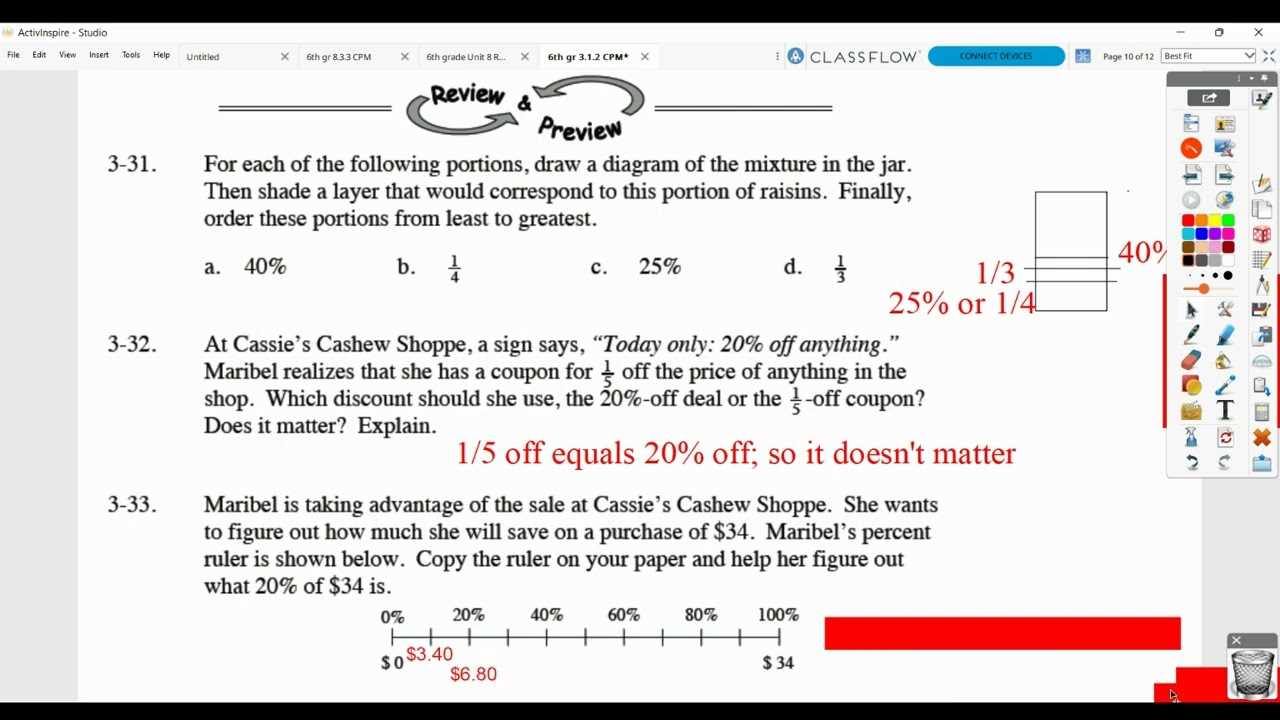
One of the primary features of a strong curriculum is its ability to introduce new concepts in a logical sequence. Each lesson is designed to build on previous knowledge, allowing students to make connections between different topics. This step-by-step progression ensures that students are not overwhelmed and can absorb each concept thoroughly before moving on to more advanced material.
Emphasis on Practical Application
Alongside theoretical lessons, a quality curriculum also focuses on the real-world application of mathematical principles. Students are encouraged to solve problems that reflect actual scenarios, helping them understand how the concepts they learn can be used outside the classroom. This approach not only reinforces learning but also prepares students for everyday problem-solving tasks in their personal and professional lives.
Strategies for Using the Answer Key Effectively
To maximize the benefits of a solution guide, it’s important to use it as a tool for learning rather than simply for checking answers. By adopting effective strategies, students can deepen their understanding and reinforce key concepts. The goal is to use the guide to clarify thought processes, identify mistakes, and develop problem-solving techniques that can be applied to future challenges.
Reviewing Step-by-Step Solutions

Instead of just looking at the final solution, students should carefully examine each step provided in the guide. This method helps to understand the reasoning behind each action taken, making it easier to grasp the logic and methods used. By breaking down the process, students can identify where they went wrong and adjust their approach in the future.
Using the Guide for Self-Assessment
Another strategy is to attempt problems on your own first before referring to the guide. Once a solution is attempted, compare it with the guide to see if the approach and results align. This process not only provides immediate feedback but also helps students develop a sense of self-reliance and confidence in their problem-solving abilities.
Common Challenges in Core Algebra

Many students face obstacles when learning mathematical concepts, especially when these concepts become more abstract and complex. Struggling with certain topics can hinder overall progress, making it essential to recognize these challenges and develop strategies to overcome them. Common difficulties often arise from misconceptions, lack of practice, or a weak understanding of foundational skills. Identifying these issues early can help students tackle them before they become bigger barriers.
| Challenge | Explanation | Solution |
|---|---|---|
| Understanding Variables | Students often find it difficult to work with variables and their representations in equations. | Use visual aids and real-life examples to help make abstract concepts more concrete. |
| Solving Equations | Steps for solving equations can be confusing, especially when balancing both sides. | Break down each step and practice with simple equations before progressing to more complex ones. |
| Factoring | Factoring expressions can be intimidating due to the variety of methods required. | Practice different techniques and reinforce the connection between factoring and other operations. |
| Word Problems | Translating real-world scenarios into mathematical equations often poses a challenge. | Start with simple problems and focus on identifying key information before forming equations. |
Overcoming these common obstacles requires consistent practice, patience, and the use of different learning tools. With the right support, students can strengthen their understanding and improve their ability to solve problems effectively.
Mastering Algebra with Answer Keys
Achieving mastery in mathematics requires consistent practice, review, and a clear understanding of the underlying principles. A useful tool in this process is the ability to check one’s solutions against a detailed guide. By comparing their methods with the correct steps, students can refine their approach and deepen their understanding of mathematical concepts.
Using solution guides effectively can help solidify key concepts and enhance problem-solving skills. When students carefully review each solution, they can identify areas where their reasoning or methods may need improvement. This allows for targeted practice and ensures that concepts are fully understood before moving on to more complex topics.
Refining Problem-Solving Techniques
Mastery comes from repetition and refinement. By practicing different types of problems and using a guide to verify each step, students learn to approach challenges with greater confidence. They also begin to recognize patterns in problem types, which aids in quicker and more efficient solutions in the future.
Building Confidence in Mathematical Abilities
With regular use of a solution guide, students gradually build the confidence needed to tackle problems independently. As they become more familiar with the process, they are less likely to second-guess themselves and more likely to apply their knowledge accurately in future problems.
Improving Problem-Solving Skills
Enhancing problem-solving abilities is crucial for students looking to succeed in mathematics and other disciplines that require logical thinking. The process of solving complex problems becomes easier with practice, critical analysis, and the application of effective strategies. With the right approach, learners can improve their ability to identify patterns, break down tasks into manageable steps, and apply learned methods confidently.
Key Techniques for Effective Problem Solving

There are several strategies that can help students become more efficient problem solvers. These techniques involve understanding the problem thoroughly, breaking it down into smaller, more manageable parts, and applying different methods to reach a solution. The ability to evaluate different approaches and choose the best one is a key skill in mastering problem-solving.
Practicing with Guided Examples
One of the most effective ways to improve problem-solving skills is through practice. Working with examples that include detailed steps can help students learn the right approach. By analyzing how problems are solved, learners can internalize strategies and apply them independently to similar tasks.
| Strategy | Benefit | Application |
|---|---|---|
| Step-by-Step Breakdown | Helps in organizing thoughts and avoiding errors. | Break large problems into smaller, solvable parts. |
| Pattern Recognition | Identifying repeating structures improves speed and accuracy. | Look for common themes in different problems. |
| Practice with Varied Problems | Exposes learners to different methods and approaches. | Solve a range of problems to develop adaptability. |
By continuously practicing and reflecting on each step, students can sharpen their problem-solving skills and approach mathematical tasks with greater ease and confidence.
Practice Problems for Mastering Mathematical Concepts
Regular practice is key to mastering any mathematical concept. To build proficiency, students need to work through a variety of problems that challenge their understanding and reinforce the skills they’ve learned. Practice problems allow learners to apply theoretical knowledge in practical ways, helping them become more confident in their ability to solve real-world tasks.
Types of Problems to Practice
Different types of problems target various skills and concepts. By practicing with a diverse range of tasks, students can strengthen their overall problem-solving abilities and prepare for more complex challenges. Problems that involve equations, graphing, and word problems each offer unique learning opportunities.
Benefits of Working Through Practice Problems
Engaging with multiple practice problems helps students identify common mistakes, learn from them, and improve over time. As they become more familiar with problem patterns, students develop the critical thinking skills needed to approach new problems with confidence.
| Problem Type | Skill Developed | Application |
|---|---|---|
| Equation Solving | Improves accuracy and understanding of operations. | Practice solving linear, quadratic, and multi-step equations. |
| Graphing | Enhances ability to visualize mathematical relationships. | Work with coordinate planes and plot functions or solutions. |
| Word Problems | Develops real-world application of mathematical concepts. | Translate word scenarios into equations for solving. |
Consistent practice with these types of problems leads to a deeper understanding of the material, allowing students to approach more advanced topics with greater ease and confidence.
How to Approach Complex Mathematical Concepts
When dealing with advanced mathematical ideas, it’s essential to approach them methodically. Many topics may seem intimidating at first, but breaking them down into smaller, more manageable parts makes them easier to understand. By building a strong foundation and practicing regularly, students can tackle even the most complex concepts with confidence.
The key to mastering difficult topics is persistence, systematic problem-solving, and learning to recognize patterns. Rather than rushing through exercises, take time to analyze each problem carefully and think critically about each step involved.
Steps for Approaching Challenging Concepts
Here are several strategies to help simplify complex topics and develop a deeper understanding:
- Break It Down: Divide complex problems into smaller steps. Focus on solving one part at a time to avoid feeling overwhelmed.
- Understand the Basics: Before tackling advanced topics, ensure that foundational concepts are well understood. This will make higher-level problems easier to solve.
- Use Multiple Resources: Don’t rely on just one source of information. Use textbooks, online tutorials, and practice problems to gain different perspectives.
- Work on Examples: Practice with a variety of example problems to understand different methods of solving similar tasks.
- Ask for Help: If stuck, seek clarification from peers, teachers, or tutors. Sometimes, a fresh perspective can make a significant difference.
Improving Through Practice
Consistent practice plays a vital role in mastering complex mathematical principles. The more problems a student solves, the better they become at recognizing strategies and applying solutions effectively. Set aside dedicated time each day to practice new concepts and revisit old problems to reinforce understanding.
- Start with simple examples and gradually increase the difficulty level.
- Review mistakes and figure out why a particular approach didn’t work.
- Challenge yourself with new problems to test your understanding and boost your confidence.
With the right approach, dedication, and persistence, complex topics can become more approachable and eventually mastered. Remember, learning is a process, and with each problem solved, progress is made.
The Role of Answer Keys in Learning
Guidelines and solution references play an important part in the educational process. They provide learners with the opportunity to verify their work, understand the reasoning behind each step, and correct any mistakes. These resources act as valuable tools in developing a deeper understanding of the material and improving problem-solving skills. By reviewing these solutions, students can see where they went wrong and learn the correct approach to each task.
In addition to helping students check their work, these solution references encourage self-reflection and critical thinking. When students compare their methods to the provided solutions, they can identify areas of weakness and find ways to strengthen their understanding of the concepts. This process fosters a more independent learning style, where students take responsibility for their progress and seek ways to improve.
Moreover, these resources can help students learn effective strategies and methods that they might not have initially considered. By studying different approaches to solving a problem, they can develop a broader toolkit of techniques for handling various types of questions. Over time, this leads to greater confidence and mastery of the subject matter.
Supporting Homework with Solution References
Homework is an essential part of the learning process, helping students reinforce their understanding and practice what they have learned in class. However, students often encounter difficulties while working on assignments, and having access to solution resources can significantly aid in overcoming these challenges. These references not only help verify answers but also serve as guides to improve comprehension and problem-solving strategies.
How Solution References Benefit Homework
Using solution references during homework offers multiple advantages that can enhance a student’s learning experience. Here are some key benefits:
- Immediate Feedback: Solution references allow students to check their work immediately and identify errors without waiting for a teacher’s review.
- Clarifying Confusion: When stuck on a problem, having access to step-by-step solutions can help clarify the correct approach and guide students toward the right path.
- Building Confidence: Being able to verify their answers helps students feel more confident about their understanding of the material.
- Improving Self-Learning: Students can learn how to solve problems on their own by understanding the methods used in the solutions, which fosters independent thinking.
Maximizing the Effectiveness of Solution References
While solution references are valuable, it’s important to use them effectively to maximize their learning potential. Here are some tips:
- Use them as a guide, not a crutch: Try to solve the problems on your own first, then check the solution to see if your approach aligns with the correct one.
- Understand the steps: Don’t just copy the solution; take time to understand each step and how it leads to the final answer.
- Review mistakes: When errors are found, analyze where you went wrong and how the solution provides a different approach.
By using these resources thoughtfully, students can transform homework into an opportunity for deeper learning and greater success.
Reviewing Mathematical Concepts in Depth
In-depth review of mathematical principles is essential for mastering the subject and building a strong foundation. By revisiting key topics and examining them from different angles, students can deepen their understanding and strengthen their problem-solving skills. This process not only helps in reinforcing the material but also in recognizing the connections between different concepts and how they apply to various problems.
Effective review involves more than just memorizing formulas or methods; it requires critical thinking and the ability to apply knowledge in various contexts. Breaking down complex ideas into smaller, manageable parts can make them easier to understand and help students see the bigger picture. By carefully working through examples and practicing a range of problems, learners gain a deeper insight into how different mathematical operations work together.
Additionally, revisiting foundational concepts regularly helps ensure that students retain what they’ve learned over time. When concepts are reviewed systematically and repeatedly, they move from short-term memory to long-term understanding, making it easier to apply them in more advanced topics.
Using the Solution Guide for Self-Assessment
Self-assessment is an essential part of the learning process, allowing students to evaluate their understanding and progress. By using solution guides, learners can reflect on their own work, identify strengths, and pinpoint areas that need improvement. This approach promotes self-reliance and encourages students to take ownership of their learning journey.
When students use a solution guide, they not only check their answers but also assess their approach to solving problems. This helps them recognize where they might have misunderstood a concept or made a calculation error. Self-assessment fosters a deeper understanding of the material by encouraging critical thinking and active learning.
Steps for Effective Self-Assessment
To make the most of the solution guide, students can follow these steps:
- Compare Results: After completing a problem, compare your solution with the one in the guide. Look for any discrepancies.
- Analyze Mistakes: If your solution differs, carefully review each step of the problem-solving process to identify where you went wrong.
- Understand the Correct Approach: Study the provided solution to understand the method used. Try to apply the same approach to similar problems.
- Practice Regularly: Use the guide frequently to assess your progress and reinforce concepts by solving similar problems.
Benefits of Using a Solution Guide for Self-Assessment
There are several advantages to using a solution guide as a self-assessment tool:
- Immediate Feedback: By checking solutions in real-time, students receive instant feedback on their work.
- Improved Problem-Solving Skills: Regular self-assessment helps identify gaps in understanding and boosts problem-solving abilities.
- Enhanced Retention: Actively reviewing solutions helps reinforce learned concepts and improves memory retention.
- Increased Confidence: Knowing that you can verify your own solutions builds confidence in your abilities.
Incorporating a solution guide into your study routine is a powerful tool for self-assessment and continuous improvement. It encourages students to be independent learners, constantly striving for better understanding and mastery of the material.
Enhancing Algebra Learning with Answer Keys
Learning mathematical concepts can be a complex process, but having the right tools can significantly improve understanding and mastery. One such tool is a detailed solution guide, which allows students to check their work and understand the steps involved in solving problems. This method offers a structured approach to learning, helping students identify where they may have gone wrong and providing insight into more efficient strategies for problem-solving.
By carefully reviewing the solutions, learners can strengthen their grasp of essential concepts and enhance their ability to tackle increasingly challenging exercises. Additionally, using these resources fosters self-confidence and independence in learning, as students can monitor their progress and refine their skills over time.
Benefits of Using a Solution Guide
- Immediate Feedback: Students can quickly identify errors and correct them, avoiding misunderstandings from carrying over to future problems.
- Understanding Step-by-Step Processes: Seeing the breakdown of complex problems helps learners understand the logical flow of mathematical reasoning.
- Boosting Confidence: Regular practice with feedback promotes self-reliance and a positive attitude towards learning.
Effective Strategies for Using Solution Guides
- Work Through Problems Independently: Attempt to solve the problems without looking at the solution guide. Only check the answers after completing the problem.
- Focus on Mistakes: When reviewing the solutions, pay close attention to where mistakes were made to learn how to avoid them in the future.
- Use Multiple Sources: Explore various resources to gain a more comprehensive understanding of concepts from different perspectives.