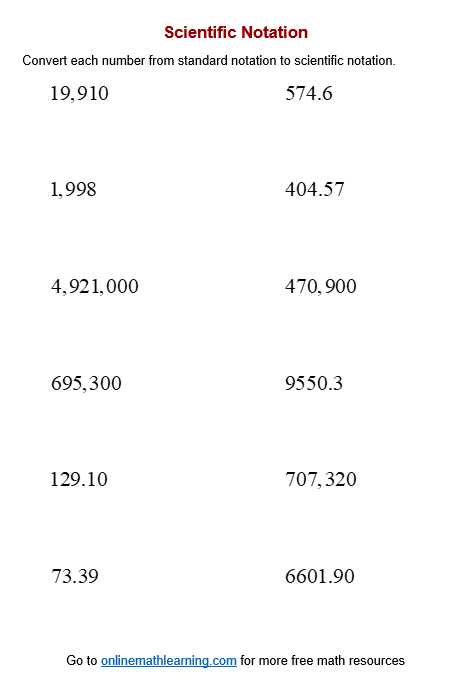
Understanding complex numerical expressions is a crucial skill in the study of various scientific fields. Often, large numbers or very small values must be represented in a way that simplifies calculations and comparisons. This is achieved through a systematic method that makes such values easier to handle without losing precision.
In this section, we focus on breaking down problems related to this numerical representation system. By practicing different types of exercises, learners can improve their ability to convert, multiply, divide, and interpret these expressions effectively. Working through sample problems and reviewing solutions provides valuable insight into mastering this concept.
With the correct approach, these calculations become less intimidating and more manageable. This resource will guide you through common challenges and offer clear, step-by-step solutions, helping you build confidence in tackling similar problems in your studies.
Chemistry Scientific Notation Worksheet Answer Key
When working with large or tiny values, it’s essential to have a reliable method for expressing them efficiently. The approach covered here simplifies the process of performing arithmetic operations with such values, making it easier to handle complex calculations in scientific settings.
Understanding the Approach

This method involves converting numbers into a compact form that makes calculations faster and more manageable. Whether you are multiplying, dividing, or adding such numbers, it’s important to grasp the basic steps required to maintain accuracy throughout the process.
- Convert the number into the appropriate form.
- Ensure the exponents are handled correctly during multiplication or division.
- Adjust the exponent when adding or subtracting values in this form.
Common Challenges and Solutions

Many students struggle with keeping track of exponents, especially when performing multiple operations in a row. Here are some common issues and solutions:
- Problem: Inconsistent exponents during addition and subtraction.
- Solution: Adjust the exponents to match before performing the operation.
- Problem: Confusing the base values during multiplication or division.
- Solution: Multiply or divide only the base numbers, while adding or subtracting the exponents as needed.
By following these steps and recognizing common mistakes, you can efficiently solve problems involving large and small numbers in any scientific context.
Understanding Scientific Notation Basics
Working with extremely large or small numbers is a common challenge in various fields, especially in science and engineering. To make such values easier to handle, a special system of expressing them is used. This system allows for simplifying the representation of numbers, making calculations more efficient and manageable.
The core idea behind this method is to express numbers as a product of two parts: a coefficient and a power of 10. This makes it easier to compare, multiply, or divide values that are otherwise difficult to work with due to their size. The main goal is to avoid writing out long strings of zeros, whether in the case of very large or very small numbers.
For example, instead of writing 0.00000045, this value can be expressed as 4.5 × 10-7, which is much simpler to read and calculate. Similarly, very large numbers like 700,000,000 can be written as 7 × 108.
By learning how to express and manipulate numbers in this form, you gain a powerful tool for solving complex problems involving measurements, distances, or quantities that span a wide range of values.
How to Solve Scientific Notation Problems
When working with expressions involving very large or small numbers, it’s important to follow specific steps to simplify and solve the problem. These steps ensure accuracy and consistency, especially when performing arithmetic operations such as multiplication, division, or addition.
The key to solving these problems lies in managing the exponents and the base values correctly. Whether multiplying, dividing, or adding, understanding how to handle the powers of ten is essential. Below are the main steps for solving problems involving this number system:
| Operation | Steps |
|---|---|
| Multiplication |
|
| Division |
|
| Addition or Subtraction |
|
By following these steps, you can easily solve problems involving large or small numbers without confusion, ensuring that the calculations remain precise and manageable.
Common Mistakes in Scientific Notation

When working with numbers in a simplified format, it’s easy to make errors that can lead to incorrect results. These mistakes often occur when handling the exponents or the base values incorrectly. Recognizing and understanding common errors is the first step in avoiding them and ensuring accuracy in calculations.
One common mistake is mismanaging the exponents during multiplication or division. It’s easy to forget to add or subtract the exponents correctly, leading to incorrect powers of 10. Another frequent issue is failing to adjust the base number properly, which can cause the entire expression to be miscalculated.
Additionally, students often struggle with ensuring consistency when adding or subtracting numbers in this format. If the exponents are not aligned, it can lead to mistakes in the final result. It’s also important to avoid confusion between the base numbers and the exponents, as mixing them up can lead to significant errors.
By being aware of these common pitfalls, you can double-check your work and avoid these mistakes, leading to more accurate results in every calculation.
Importance of Scientific Notation in Chemistry
In fields that involve measurements across a wide range of values, expressing numbers in a compact form is essential for clarity and efficiency. This method of representing numbers not only simplifies complex calculations but also ensures that the values are both precise and easy to understand. It plays a crucial role in managing the scale of data, whether dealing with extremely large quantities or minuscule values.
Efficient Handling of Extreme Values
In scientific research, measurements can span several orders of magnitude, from subatomic particles to vast astronomical distances. This approach allows scientists to express these values without writing out long strings of zeros, making both communication and calculations more efficient. Whether it’s working with particle sizes or vast astronomical measurements, the method ensures that these numbers are easily interpretable and manageable.
Accuracy and Precision in Calculations
When conducting experiments or making predictions, precision is key. By converting numbers into this condensed form, researchers can maintain accuracy in their calculations while avoiding errors that might arise from using unwieldy values. This format also reduces the chances of rounding errors, which can become significant in detailed scientific work.
Overall, this system is vital for making sense of the vast amounts of data encountered in scientific studies, ensuring that measurements and calculations remain consistent and understandable across various disciplines.
Step-by-Step Guide to Scientific Notation

Converting large or small numbers into a more manageable form is a fundamental skill when dealing with complex calculations. This process simplifies numbers, making them easier to read, compare, and perform operations on. The following guide will walk you through the necessary steps to accurately convert and work with these values.
First, identify the decimal point in the number. If you are working with a large number, move the decimal point to the left so that there is only one non-zero digit to its left. For small numbers, move the decimal to the right. The number of places you move the decimal will determine the exponent of 10.
Next, write the number as a product of the shifted base value and 10 raised to the appropriate power. The exponent reflects how many places the decimal point was moved. For large numbers, the exponent is positive, and for small numbers, the exponent is negative.
For example, the number 450,000,000 can be written as 4.5 × 108, while 0.00000045 becomes 4.5 × 10-7.
With these basic steps in mind, you can now easily convert any number into its simplified form, which will be useful in performing various mathematical operations efficiently.
Converting Numbers to Scientific Notation
When dealing with very large or very small numbers, it’s often necessary to convert them into a more concise and manageable form. This simplified method allows for easier calculations, comparisons, and understanding. The process involves adjusting the position of the decimal point and expressing the number as a product of a base and a power of ten.
The first step in this conversion is to identify the decimal point in the number and move it so that only one non-zero digit remains to its left. For larger values, this will involve shifting the decimal point to the left; for smaller values, to the right. The number of decimal places moved determines the exponent of 10.
For instance, if the number is 850,000,000, move the decimal to create 8.5, and count the number of places it was shifted (in this case, 8). This gives the result 8.5 × 108. Conversely, for a small number like 0.000056, you would shift the decimal point to get 5.6, and since the decimal was moved five places to the right, the result would be 5.6 × 10-5.
Once you understand the basic steps, converting any number to this format becomes straightforward, making it easier to perform complex calculations and understand the magnitude of the values involved.
Multiplying and Dividing in Scientific Notation
When working with numbers in simplified form, performing multiplication or division involves handling both the base values and the powers of ten. These operations follow specific rules that ensure accuracy, making it easier to work with very large or small quantities.
Multiplying Numbers in Simplified Form
To multiply numbers in this format, follow these steps:
- Multiply the base numbers as you would normally.
- Add the exponents of the powers of ten together.
- Write the result as a product of the new base and the combined exponent.
For example, if you are multiplying 3 × 104 by 2 × 103, you would first multiply the base numbers (3 × 2 = 6) and then add the exponents (4 + 3 = 7). The result would be 6 × 107.
Dividing Numbers in Simplified Form
When dividing, the process is slightly different:
- Divide the base numbers as usual.
- Subtract the exponent of the denominator from the exponent of the numerator.
- Write the result as a quotient of the new base and the difference of the exponents.
For instance, if dividing 6 × 107 by 3 × 102, divide the base numbers (6 ÷ 3 = 2) and subtract the exponents (7 – 2 = 5). The result is 2 × 105.
By following these rules, multiplying and dividing numbers in this simplified format becomes much easier, allowing for quick and accurate calculations in complex problems.
Real-Life Applications of Scientific Notation

In many fields, large and small values are common and need to be expressed in a way that simplifies calculations and communication. For everyday use, these methods make handling complex numbers much more manageable, whether in scientific research, engineering, or technology. By using concise expressions, we can focus on the magnitude of numbers without becoming overwhelmed by zeros or decimals.
Astronomy relies heavily on these methods to express distances between celestial bodies. For instance, the distance from Earth to distant stars is often represented by extremely large numbers, and compact expressions allow for more efficient communication of vast distances. Similarly, in physics, when measuring forces and energies at microscopic scales, tiny values are condensed into forms that are easier to work with and interpret.
Another common use is in the medical field, where the sizes of cells and viruses can be measured in nanometers. Expressing these minute measurements in a condensed form makes them more accessible to researchers and doctors. Computational fields, such as computer science, also use these methods to handle data sizes, storage capacities, and processing speeds that span across large scales.
Interpreting Scientific Notation in Chemistry
When dealing with extremely large or small quantities, it’s essential to express them in a way that is both efficient and understandable. This approach allows professionals to handle measurements and calculations with precision, without getting bogged down by unwieldy numbers. Understanding how to read and convert these compact expressions is vital for accurate communication in various scientific contexts.
In practice, values that represent things like atomic masses, molecular sizes, and reaction rates are often too large or too tiny to be written in their full form. Instead, they are expressed using a simplified method that maintains their significance. Below are key points to keep in mind:
- Large numbers: When numbers are extremely large, they are expressed with a positive exponent. For example, 6,000,000,000,000 can be written as 6 x 1012.
- Small numbers: Conversely, very small numbers are written with a negative exponent. For example, 0.000000003 can be represented as 3 x 10-9.
- Units of measurement: These expressions also work in tandem with units, such as moles or grams, to convey quantities in a compact and readable form.
By mastering these methods, students and professionals can more easily interpret data, perform calculations, and understand complex phenomena in their respective fields.
Common Chemistry Problems with Scientific Notation
In various scientific problems, working with extremely large or small quantities can be challenging. When these values are represented in a compressed form, it simplifies the handling of such data but also introduces specific difficulties. Understanding how to manipulate and interpret these compact expressions is crucial for solving common problems in labs, research, and exams.
One of the most frequent issues involves converting between different forms of these compact expressions, particularly when adding, subtracting, or comparing values. To ensure accuracy in calculations, it is important to adjust the exponents and align the values correctly. Below is a table showing common problems and their solutions:
| Problem | Solution |
|---|---|
| Adding or subtracting numbers with different exponents | Adjust the exponents to be the same, then proceed with the operation. |
| Multiplying numbers with different exponents | Multiply the coefficients and add the exponents. |
| Dividing numbers with different exponents | Divide the coefficients and subtract the exponents. |
| Converting to standard form | Move the decimal point and adjust the exponent accordingly. |
These common issues can be easily managed once the basic rules are understood, leading to more efficient problem-solving in related fields.
Tips for Mastering Scientific Notation

Mastering the process of expressing large and small numbers in a simplified form is crucial for solving many problems in science. Gaining proficiency in these methods not only improves accuracy but also speeds up calculations, especially when dealing with complex data. The following tips will help you become more comfortable with these condensed expressions and avoid common mistakes.
Understand the Rules

One of the first steps to mastering this method is understanding the fundamental rules, such as how to handle exponents, coefficients, and conversions between forms. For example, when multiplying numbers, always add the exponents. Likewise, when dividing numbers, subtract the exponents. By knowing these basic principles, you can easily navigate through calculations and conversions.
Practice Regularly
The more you practice, the more intuitive it becomes. Regular practice with problems that involve adding, subtracting, multiplying, and dividing these compact forms will help reinforce your skills. Below is a table with helpful strategies to guide your practice:
| Tip | Description |
|---|---|
| Work with simple numbers | Start with easier numbers and gradually increase complexity to build confidence. |
| Check your exponents | Always verify that your exponents are aligned when adding or subtracting numbers. |
| Use a calculator | For quick calculations, especially with large numbers, use a scientific calculator to ensure accuracy. |
| Convert between forms | Practice converting between full numbers and their condensed forms to solidify your understanding. |
With consistent practice and a clear understanding of the fundamental rules, mastering this method will become a natural part of problem-solving in scientific contexts.
Scientific Notation in Chemical Equations
In many reactions and processes, numbers involved are either extremely large or small, making them cumbersome to express in their full form. Using a compact format for these values helps simplify calculations and ensures accuracy in equations, especially when dealing with quantities such as molecular masses, reaction rates, and concentrations. This approach is especially useful when representing values in a more manageable and readable way for both lab work and theoretical calculations.
Applying Compact Expressions to Reactions
When writing chemical equations, certain quantities, such as the number of molecules or moles, can be extremely large. Instead of writing out all the zeros, these quantities are often expressed in a more concise way. For example, Avogadro’s number, 6.022 x 1023, is frequently used to represent the number of particles in one mole of a substance. This expression makes the large number easier to handle without losing any precision in calculations.
Examples in Stoichiometry
Stoichiometric calculations often involve manipulating large quantities of reactants or products. By expressing these values in a condensed format, you can easily perform conversions without the risk of introducing errors due to lengthy, cumbersome numbers. Below is an example of how compact expressions help in balancing chemical equations:
Example: Consider a reaction where 1.5 x 103 moles of a substance react with 4.0 x 102 moles of another substance. By using these simplified expressions, it’s easier to compute the amounts needed for complete reaction and ensure proper proportions are maintained.
Using Worksheets to Practice Scientific Notation

Practicing with exercises is one of the best ways to gain confidence and mastery over expressing large and small numbers in a compact format. These practice materials provide a structured way to apply the rules and solve problems step by step. By consistently working through such tasks, you can solidify your understanding and improve accuracy when handling complex calculations.
Benefits of Practice Materials
Exercises designed to focus on these compact expressions allow learners to work with a variety of problems, from simple conversions to more complex calculations involving addition, subtraction, multiplication, and division of these compact forms. Regular practice with different types of problems helps develop a deeper understanding of how to apply the rules efficiently in real-world scenarios.
Structured Problem-Solving
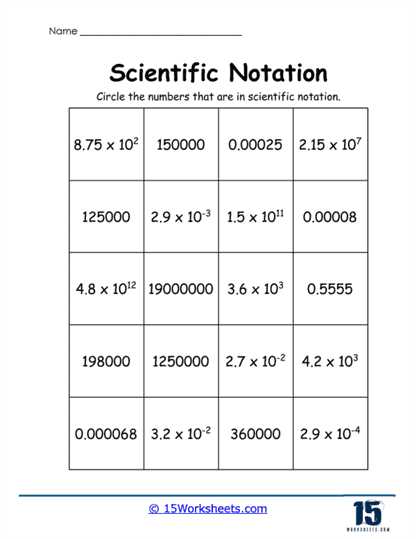
By using structured tasks, you can break down complex problems into manageable steps. These problems often include helpful prompts and examples to guide your approach. The more you practice these tasks, the quicker you’ll become at identifying the best strategies for solving different types of problems involving large and small quantities. With each exercise, you’ll refine your skills, making the process easier and more intuitive.
Benefits of Worksheets for Learning Chemistry
Practice materials play an essential role in helping learners develop a deeper understanding of complex subjects. They provide a structured approach to reinforce concepts, allowing students to apply what they’ve learned in a practical way. These resources offer a variety of problems and challenges that encourage critical thinking and problem-solving, helping learners to solidify their knowledge and improve their skills over time.
One of the key advantages of such materials is that they allow for independent practice, giving students the opportunity to work at their own pace. This type of learning promotes active engagement with the material and helps to identify areas that need improvement. Additionally, these exercises often include clear examples and step-by-step solutions, making them an invaluable tool for both beginners and those looking to refine their expertise.
By working through different types of problems, students can gain a more thorough grasp of important concepts, preparing them for more advanced topics. Regular use of these resources fosters confidence and proficiency, which are crucial for success in academic and professional settings.
Resources for Learning Scientific Notation

There are a variety of tools and materials available to help learners master the process of expressing large and small values in a compact form. Whether you are just starting out or looking to refine your skills, these resources can guide you through the basics and provide practice for more advanced applications. The right resources make it easier to understand the rules and apply them in different scenarios.
Books and Textbooks
Textbooks often provide in-depth explanations, clear examples, and practice problems that are crucial for building a solid understanding. Many of these resources break down complex concepts into smaller, more manageable parts. Look for textbooks that include:
- Step-by-step explanations
- Practice problems with solutions
- Examples from real-world applications
Online Resources and Tools
In addition to textbooks, there are numerous online platforms that offer interactive lessons, video tutorials, and exercises to help reinforce learning. These resources can provide immediate feedback, helping you track progress and identify areas for improvement. Here are some types of online resources to explore:
- Interactive calculators: Tools that allow you to practice conversions and calculations instantly.
- Educational websites: Platforms offering lessons, quizzes, and challenges that cover different aspects of working with compact expressions.
- Video tutorials: Videos that break down each step of using compact expressions in both simple and complex problems.
By combining these resources, learners can build a deeper understanding, reinforce concepts, and practice at their own pace to gain mastery in handling compact values.