
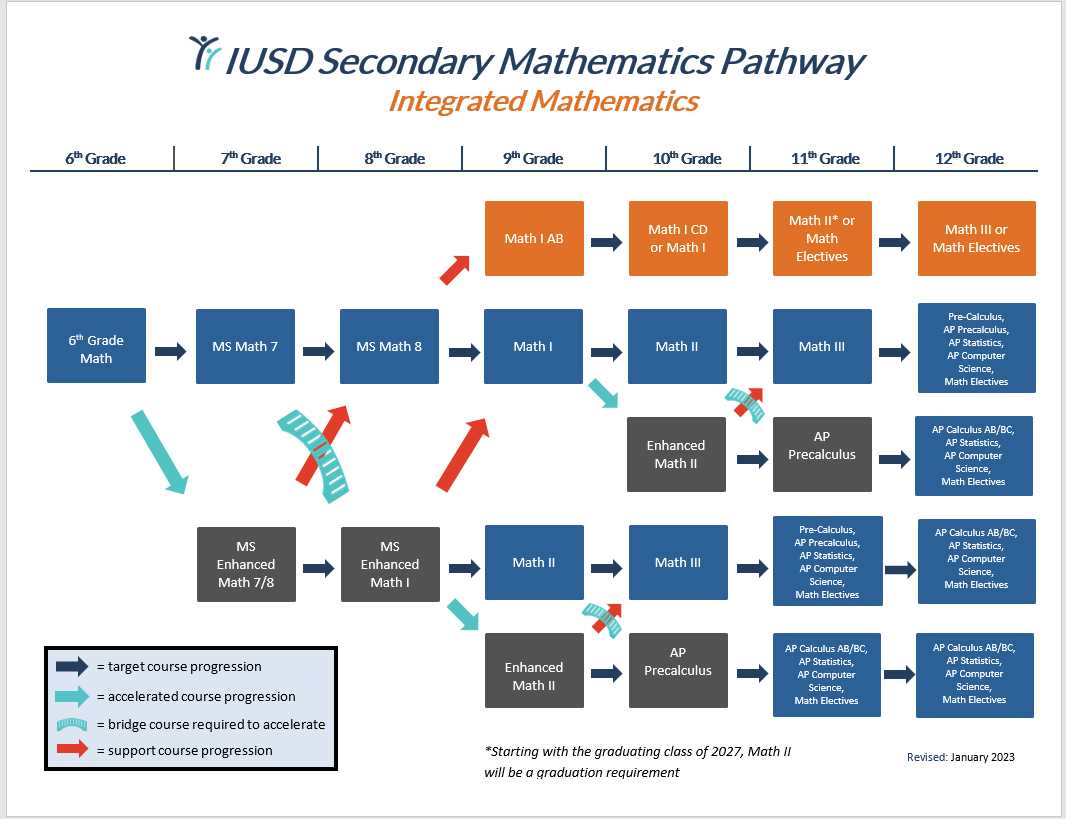
In any academic journey, having the right resources can make all the difference. Whether you’re navigating complex challenges or reinforcing your understanding, the ability to access reliable solutions is essential. This guide offers a deep dive into helpful strategies, offering support for students seeking clarity and better results in their studies.
Understanding the materials presented is just one part of the equation; knowing how to apply the information effectively is where true mastery happens. With structured practice and problem-solving techniques, you can enhance your approach, gain confidence, and improve your overall performance. By using this resource, students can review their work, ensure accuracy, and advance at their own pace.
Big Ideas Math Course 2 Accelerated Answer Key

When tackling challenging assignments and exercises, having reliable resources to verify solutions can significantly boost understanding and retention. This section focuses on providing essential support for learners as they navigate through various tasks. By using this material, students can confidently check their responses and strengthen their grasp on important concepts.
How to Use This Resource
This tool is designed to assist students in reviewing their work with accuracy and precision. By referring to the solutions provided, learners can cross-check their methods, identify mistakes, and correct any misconceptions. Here’s how you can effectively make use of the resource:
- Verify your solutions after completing each section.
- Analyze step-by-step explanations to understand how each problem is solved.
- Use the resource to reinforce areas where you may need additional practice.
- Build confidence by solving problems independently, then comparing results.
Benefits of Using This Resource
By integrating this support system into your study routine, you can achieve several benefits:
- Clarify complex concepts that may have caused confusion.
- Learn efficient problem-solving strategies to save time and effort in exams.
- Improve accuracy through consistent self-checking.
- Gain a deeper understanding of the methods behind each solution.
Overview of Big Ideas Math Course 2
This section provides a comprehensive look at the structure and content of a program designed to build foundational skills in advanced problem-solving. The material is tailored to guide learners through progressively complex concepts, ensuring mastery at each level before advancing further. Students engage with topics that expand their ability to think critically and solve problems efficiently.
The curriculum emphasizes practical application of mathematical principles through exercises, challenges, and examples. Each module is crafted to foster a deep understanding of the topics, supporting learners in developing both their technical abilities and their logical reasoning. By working through these exercises, students gain the tools they need to succeed in both academic settings and real-world scenarios.
Key Concepts in Accelerated Math 2

This section delves into the essential principles covered in an advanced level of the subject, highlighting the foundational elements students must grasp to build a strong mathematical base. Emphasizing both conceptual understanding and practical application, learners are encouraged to think critically and solve problems methodically. This approach allows students to move from basic to more complex ideas with ease.
Understanding Core Topics
Throughout the program, several key areas are explored in depth. These concepts provide the building blocks for more advanced work in mathematics and are integral to mastering the material. The following table outlines some of the central topics covered:
| Concept | Description |
|---|---|
| Algebraic Expressions | Understanding variables, coefficients, and constants and how to simplify and manipulate expressions. |
| Linear Equations | Solving equations involving variables and constants using basic operations and graphing techniques. |
| Fractions and Decimals | Working with ratios, proportions, and performing operations on fractions and decimal numbers. |
| Geometry Basics | Exploring shapes, angles, area, and perimeter to understand the principles of spatial relationships. |
| Problem Solving Strategies | Using systematic approaches to solve real-world problems by applying mathematical techniques. |
Building on These Foundations
As students become more comfortable with these concepts, they will be able to tackle increasingly complex problems. By mastering these foundational elements, learners can confidently progress to higher-level topics and gain the skills necessary for success in future mathematical endeavors.
How to Use the Answer Key Effectively
Using a solution guide effectively can greatly enhance a student’s ability to understand complex concepts and improve their performance. Rather than simply checking answers, it is important to engage with the solutions in a way that fosters deeper understanding. This section outlines practical steps to make the most of this resource, turning it into an active learning tool rather than a passive reference.
Review Your Work Step-by-Step
After completing an exercise or problem set, refer to the solution guide and go through each step carefully. Pay attention not only to the final result but also to the methods used to reach that conclusion. This will help you understand the reasoning behind the process and identify areas where you may need further practice.
Identify and Correct Mistakes
If your solution differs from the provided result, don’t just move on. Take the time to compare each step and pinpoint where things went wrong. Understanding your mistakes is a crucial part of the learning process and will help you avoid making the same errors in the future.
Understanding the Course Structure
To succeed in any program, it’s crucial to understand its layout and flow. The structure of the material is designed to gradually introduce more advanced concepts while reinforcing foundational skills. Knowing how the lessons and exercises are organized will help you navigate the content more effectively, ensuring you can build on what you’ve learned without feeling overwhelmed.
Lesson Breakdown
The curriculum is divided into sections, each focusing on a specific set of concepts or skills. Each part includes various activities, practice problems, and examples to illustrate key points. This methodical progression allows students to gain confidence in simpler topics before moving on to more complex challenges. Understanding this structure can help you pace yourself and identify which areas require additional focus.
Building a Strong Foundation
Earlier sections are designed to establish a strong base, focusing on fundamental techniques that are essential for tackling more difficult problems later on. The structured approach ensures that students are not only learning but mastering the necessary steps before advancing. By following this logical progression, learners can more easily grasp higher-level topics and apply their knowledge effectively.
Breaking Down Chapter 1 Answers
Understanding the solutions to the first chapter is essential for setting the stage for the rest of the program. This section focuses on the step-by-step breakdown of the exercises, helping students grasp the reasoning behind each solution. By carefully analyzing the solutions provided, learners can see how foundational concepts are applied in different problem-solving scenarios.
The first chapter typically covers basic concepts that are built upon throughout the program. By thoroughly reviewing the provided solutions, students can strengthen their understanding of these essential principles, ensuring a solid foundation for more advanced material. Each answer is accompanied by detailed explanations that demonstrate how to approach similar problems in the future.
How to Tackle Word Problems

Word problems often present unique challenges that require a mix of comprehension and problem-solving skills. Unlike straightforward equations, these problems involve interpreting a situation and translating it into a mathematical model. Developing a systematic approach to these types of exercises will make them easier to understand and solve effectively.
Identify Key Information
The first step in solving any word problem is to carefully read through the text and identify the key details. Focus on numbers, units, and any relationships or conditions described. Highlighting or underlining important pieces of information can help you stay organized and ensure that nothing is overlooked.
Formulate a Strategy
Once the key elements are identified, the next step is to determine which mathematical operations or formulas are needed. Think about how the problem can be broken down into smaller steps. Whether it’s an equation, a ratio, or a geometry problem, formulating a strategy will guide you toward the correct solution.
Strategies for Solving Equations
Solving equations involves a systematic approach to isolate variables and find their values. Whether dealing with simple linear equations or more complex expressions, having a reliable strategy can make the process more efficient and less confusing. The key is to break down each problem into manageable steps, applying logical methods to simplify and solve the equation correctly.
One effective strategy is to perform the same operation on both sides of the equation to maintain equality. This principle ensures that the relationship between the terms remains balanced as you manipulate the equation. Additionally, always look for opportunities to combine like terms or factor expressions to make the equation simpler before proceeding with further calculations.
Practice Tests and Answer Key Insights
Practice tests serve as a valuable tool for reinforcing concepts and assessing your understanding of the material. By regularly completing these tests, you can gauge your progress, identify areas that need improvement, and prepare effectively for assessments. However, simply taking the test is not enough–reviewing the provided solutions is crucial to gaining deeper insights and improving your problem-solving strategies.
After completing a practice test, it’s essential to carefully analyze each solution. This process helps you understand the correct methods and pinpoint where mistakes were made. Here are some steps to follow when reviewing your results:
- Compare Step-by-Step: Look at each solution closely to understand how the problem was approached. This will help you identify any steps you missed or misunderstood.
- Understand Mistakes: If your solution differs from the provided one, focus on the specific errors you made. Was it a calculation mistake or a misunderstanding of the concept?
- Rework Problems: If you’re struggling with a particular problem, redo it without looking at the solution to reinforce your understanding.
- Clarify Uncertainty: If you’re unsure about why a solution works, seek additional resources or ask for clarification to solidify your grasp of the concept.
By using practice tests and reviewing the provided solutions carefully, you not only improve your problem-solving skills but also build the confidence needed to tackle more advanced topics with ease.
Common Mistakes in Course 2 Math
In any academic subject, it’s easy to fall into certain traps that can lead to errors in problem-solving. When tackling the exercises in this program, students often encounter common pitfalls that can hinder their progress. Recognizing and addressing these mistakes early on is essential for improving accuracy and developing a deeper understanding of the material.
One of the most frequent mistakes is misinterpreting word problems or overlooking key information within the question. Students may rush through the problem and miss crucial details, which can lead to incorrect solutions. Another common issue is neglecting to follow the proper order of operations, which can result in mathematical errors in multi-step problems. Additionally, students sometimes overlook the importance of checking their work, which can cause simple calculation errors to go unnoticed.
Mastering Fractions and Decimals
Understanding the relationship between fractions and decimals is a crucial skill in many areas of mathematics. These concepts allow students to express quantities in different forms, and mastering them is key to solving a wide range of problems. Whether you’re comparing values, performing calculations, or converting between forms, a strong grasp of fractions and decimals will enhance your overall problem-solving abilities.
One common challenge is converting between fractions and decimals. By learning the basic conversion methods and practicing them regularly, you can easily switch between the two forms depending on the problem you’re solving. Additionally, understanding how to perform arithmetic operations with fractions and decimals, such as addition, subtraction, multiplication, and division, is essential for mastering these topics.
| Fraction | Decimal |
|---|---|
| 1/2 | 0.5 |
| 1/4 | 0.25 |
| 3/4 | 0.75 |
| 1/5 | 0.2 |
With regular practice and a focus on understanding the underlying principles, you can easily master fractions and decimals, and apply them effectively in more complex problems.
Tips for Success in Accelerated Math
Achieving success in an advanced level of mathematics requires more than just understanding the basics. It involves developing a structured approach to learning, staying organized, and consistently practicing complex concepts. With the right mindset and strategies, you can confidently tackle challenging problems and excel in the subject.
One key to success is breaking down each problem into manageable steps. Instead of rushing to get to the solution, take time to understand the question and outline the necessary steps to solve it. Additionally, regularly reviewing and practicing previous topics will help reinforce your skills and build confidence for tackling more advanced problems.
| Tip | Explanation |
|---|---|
| Stay Organized | Keep a clear record of your work, notes, and solutions to easily track progress and revisit concepts as needed. |
| Practice Regularly | Daily practice helps solidify concepts and improves speed and accuracy in solving problems. |
| Focus on Understanding | Instead of memorizing procedures, strive to understand the reasoning behind each method for better long-term retention. |
| Ask for Help | If you’re struggling with a concept, don’t hesitate to seek guidance from teachers or peers. |
By following these strategies and staying persistent, you will be well on your way to mastering advanced topics and succeeding in mathematics.
Exploring Advanced Topics in Course 2
As you progress through more advanced levels of mathematics, it’s important to build on foundational knowledge while delving into more complex concepts. These advanced topics not only expand your understanding but also prepare you for higher levels of study. Exploring these areas can enhance your problem-solving abilities and develop critical thinking skills.
In this stage, students often encounter a range of topics that challenge their existing knowledge and require deeper analysis. To successfully master these subjects, it’s essential to approach each one systematically and break down the concepts step by step. Below are some of the advanced topics commonly explored:
- Solving Systems of Equations: Learn how to solve multiple equations simultaneously using various methods such as substitution and elimination.
- Exponents and Radicals: Understand the properties of exponents and how to simplify expressions involving roots and powers.
- Polynomials: Explore the different types of polynomials and how to perform operations such as addition, subtraction, and multiplication.
- Rational Expressions: Study fractions with polynomials in the numerator and denominator, and learn how to simplify and solve them.
- Functions and Graphing: Delve into the relationships between variables and how to graph functions on the coordinate plane.
By actively engaging with these topics and practicing regularly, students can gain a thorough understanding of advanced mathematical concepts and apply them with confidence in various real-world scenarios.
Why Answer Keys Are Important
In any academic setting, being able to verify your work is crucial for growth and improvement. Having a tool to compare your solutions against allows for quick self-assessment and helps to identify where mistakes may have occurred. This process not only helps you correct errors but also reinforces the learning process, providing clarity on complex concepts and problem-solving strategies.
When tackling difficult problems, it’s easy to overlook small mistakes or misunderstand the methods. The ability to cross-check your solutions ensures that you’re on the right track and gives you the confidence to move forward. Additionally, answer guides can provide insight into different ways to approach a problem, offering alternative methods that may be more efficient or easier to understand.
Guiding Self-Reflection

By reviewing solutions after completing exercises, you can gain valuable feedback on your understanding. This self-reflection enables you to pinpoint areas for improvement and adjust your study strategies accordingly.
Enhancing Problem-Solving Skills

Answer guides not only confirm correctness but also highlight the process behind each step. This deeper understanding of the reasoning involved in each solution can improve your overall problem-solving skills, making you more efficient and effective in future tasks.
Steps to Review Your Math Work
Reviewing your work is an essential part of mastering any subject. Taking the time to carefully analyze each step of your process ensures that you understand the concepts and helps you identify any errors that may have been made. This practice not only improves your accuracy but also deepens your comprehension, allowing you to build a stronger foundation for future problems.
Effective review involves more than simply checking if the final answer is correct. It requires a thoughtful process of retracing your steps, examining each calculation, and understanding the logic behind the methods used. By following a structured approach, you can gain confidence in your work and ensure that you’re on the right track.
Step 1: Check for Calculation Mistakes

Begin by carefully reviewing your calculations. Ensure that all arithmetic operations are performed correctly, paying close attention to signs and decimal places. It’s easy to make simple errors that can lead to incorrect results.
Step 2: Revisit Problem-Solving Strategies
Next, look back at the methods you used to solve the problem. Are there alternative strategies that might have been more effective? Consider whether there is a different approach that would lead to the same or better results. This helps you refine your problem-solving skills for the future.
How to Prepare for Exams
Effective preparation is the key to success in any test. By adopting the right strategies, you can improve your understanding of the material and perform confidently when it’s time to take the exam. Preparation should go beyond simply memorizing formulas and procedures; it requires practicing problem-solving techniques and reinforcing the concepts behind each task.
The best way to prepare is to break down the material into manageable sections and create a study plan. This way, you’ll avoid cramming and allow yourself enough time to focus on the areas that need more attention. With the right approach, you can feel fully prepared and ready to tackle any questions on the test.
Step 1: Review Core Concepts
- Identify the key topics that will appear on the exam.
- Revisit any areas where you feel less confident and review your notes or textbooks.
- Make sure you understand the basic principles that underpin each type of problem.
Step 2: Practice Regularly
- Work through practice problems to solidify your understanding.
- Simulate test conditions by timing yourself while solving problems.
- Focus on problem types that you struggle with the most to build confidence in those areas.
Step 3: Review Mistakes and Seek Help
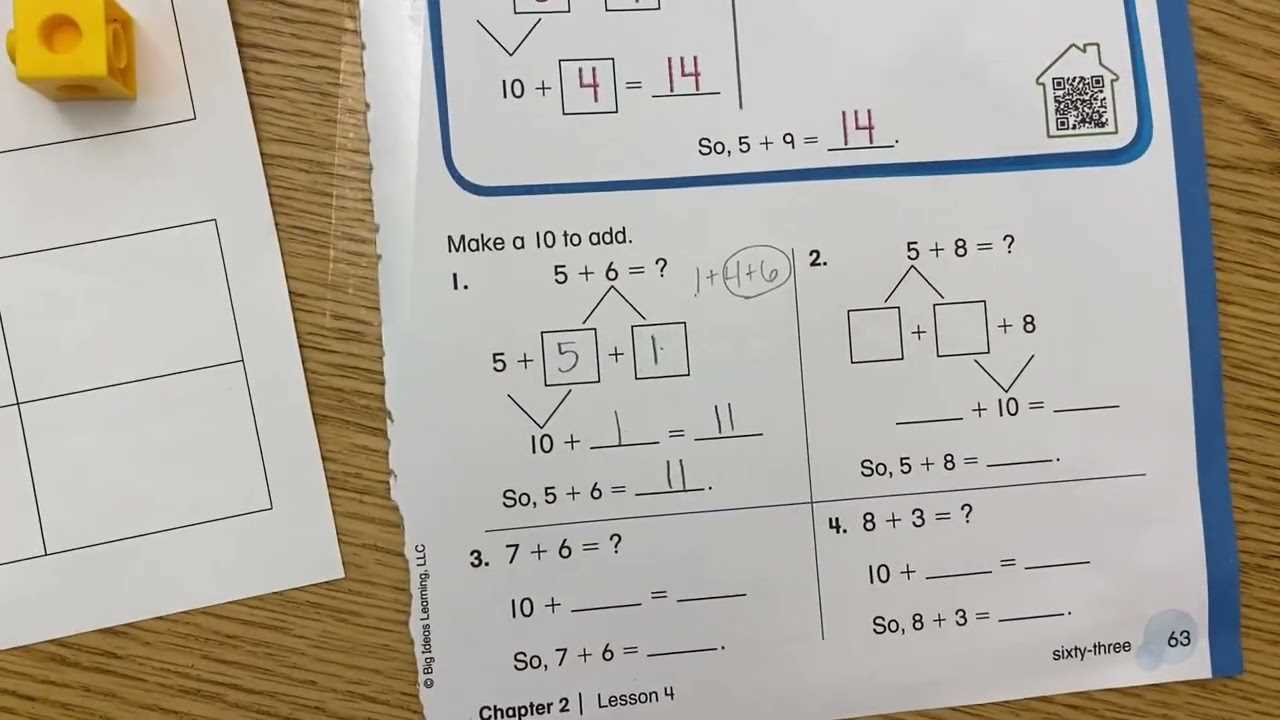
- If you make mistakes, take the time to understand where you went wrong.
- Seek clarification from teachers or classmates on any concepts that remain unclear.
- Consider discussing difficult topics in study groups for additional support.
By following these steps and staying organized, you’ll improve your readiness for the exam and reduce any last-minute stress. Remember, consistent practice and understanding are the keys to mastering any subject and excelling in your exams.
Improving Your Problem-Solving Skills
Strong problem-solving skills are essential for mastering any subject. The ability to approach challenges methodically and find solutions efficiently is a skill that can be developed over time. Whether it’s breaking down complex questions or applying logical steps, becoming better at solving problems will not only help you in tests but also enhance your overall understanding of the material.
The key to becoming proficient in problem-solving lies in consistent practice, recognizing patterns, and adopting a step-by-step approach. By developing strategies to analyze each question thoroughly, you’ll gain more confidence in your abilities and find that solving problems becomes increasingly intuitive.
Step 1: Understand the Problem
Before diving into any solution, it’s crucial to fully understand what the problem is asking. Take a moment to read the question carefully and identify the known and unknown information. Often, breaking down a complex problem into simpler parts will make it easier to approach.
Step 2: Develop a Strategy
- Consider different methods that could be used to solve the problem, such as working backwards or drawing diagrams.
- Identify patterns or similar problems that you’ve encountered before to help guide your solution process.
- Plan out your approach step by step to avoid rushing through and missing important details.
Step 3: Practice Regularly

- The more problems you solve, the better you’ll become at identifying the most efficient strategies for different types of questions.
- Practice regularly to reinforce your knowledge and to become more comfortable with various problem types.
- Don’t be afraid to challenge yourself with more difficult problems to expand your problem-solving abilities.
By applying these methods and remaining patient with the learning process, you’ll find that your problem-solving skills improve significantly. Over time, solving problems will become second nature, allowing you to tackle even the most challenging questions with confidence.
Resources for Extra Practice

Supplementary materials can provide a significant boost to your learning process. Whether you need additional exercises or detailed explanations, there are plenty of resources available to help you strengthen your skills. These tools offer targeted practice, enabling you to master difficult concepts and reinforce your understanding.
Here are some great resources that can support your efforts to improve your abilities:
Online Platforms
- Khan Academy: Offers free lessons and practice exercises on a wide range of topics, allowing you to learn at your own pace.
- Wolfram Alpha: A computational engine that can solve problems and show step-by-step solutions, ideal for checking your work.
- IXL: Provides personalized practice problems with immediate feedback, designed to help you master each topic.
Books and Workbooks
- Practice Makes Perfect:: A workbook with problems and solutions designed to strengthen foundational concepts.
- Problem-Solving Strategies: A book that offers techniques and exercises to improve problem-solving approaches.
Study Groups and Tutors
- Peer Study Groups: Collaborating with classmates allows you to share knowledge and tackle difficult problems together.
- Private Tutors: One-on-one support from a tutor can provide tailored guidance and explanations to address specific challenges.
Using these resources will give you extra practice and help you build confidence in your skills. The more you engage with these tools, the more proficient you’ll become in solving problems and understanding the material at a deeper level.