
Understanding the principles behind certain statistical concepts is essential for effectively solving problems that involve randomness and variability. This section aims to guide you through key ideas, providing you with the tools to tackle related challenges confidently. Whether you’re dealing with data sets or need to interpret real-world scenarios, grasping these fundamental topics will enhance your problem-solving skills.
Practice and preparation are crucial to mastering this material. Familiarity with key terms, calculations, and methods is necessary to approach each challenge with clarity. As you work through exercises and apply the concepts, you’ll gain a deeper understanding and improve your ability to make accurate assessments.
By exploring different examples and carefully analyzing each step, you’ll be equipped to handle a variety of scenarios. With the right approach, you can develop both speed and precision, allowing you to solve problems efficiently and with confidence.
Key Concepts in Normal Distribution
Understanding the fundamental principles behind statistical models involving symmetry and bell-shaped curves is essential for solving various problems. This section will focus on the key ideas that help you navigate through such models, laying the foundation for accurate calculations and interpretations. A strong grasp of these concepts is vital to approach challenges with confidence.
Some of the most critical ideas include:
- Central Tendency: This refers to the central point around which data points are evenly distributed. It typically includes the mean, median, and mode.
- Symmetry: A distribution is symmetric when the left and right halves are mirror images of each other, reflecting balance in the data.
- Probability Density: This is a measure of the likelihood of different outcomes within a given range, often represented by a curve.
- Standard Deviation: A measure of how spread out the values are around the central point, giving insight into the data’s variability.
In addition to these, the concept of the bell-shaped curve plays a pivotal role. It helps illustrate how values tend to concentrate around the central point with fewer occurrences as you move farther away.
Key to working with these models is understanding the relationship between probabilities and specific values. By examining the symmetry and spread of data, you can determine how likely an event is to fall within certain intervals.
These foundational concepts provide the building blocks for solving complex problems and interpreting results accurately. The next step is to apply these ideas to various scenarios, sharpening your ability to make precise predictions based on the data at hand.
Understanding the Standard Normal Curve

The standard curve is a vital concept in statistics, used to represent the distribution of a set of data. This curve is essential for understanding how values are spread around a central point, and how to calculate the likelihood of specific outcomes. The curve is symmetrical, with the highest point at the center, gradually tapering off towards the ends. This shape indicates how most occurrences are concentrated around the mean, with fewer instances as you move away from it.
Key Characteristics of the Curve
One of the primary features of the curve is its symmetry, which means that the left and right halves are mirror images. This symmetry ensures that the probability of values above and below the central point is equal. The peak of the curve represents the mean value, with the spread determined by the standard deviation. The wider the spread, the greater the variability in the data.
The Role of Z-Scores
Z-scores are a key tool in understanding the position of a value within this curve. They allow you to measure how many standard deviations a value is from the mean. A z-score of 0 indicates the value is exactly at the mean, while positive or negative values represent positions above or below the center. By calculating z-scores, you can determine the probability of certain outcomes within a given range.
How to Calculate Z-Scores

Calculating z-scores is a crucial step in understanding how individual values compare to the overall spread of data. The z-score represents the number of standard deviations a particular value is from the mean. This standardization allows you to assess how typical or extreme a value is within a data set. A z-score is particularly useful when comparing values from different data sets or distributions, as it provides a consistent measure regardless of the scale of the original data.
The formula to calculate the z-score is as follows:
Z = (X – μ) / σ
Where:
- X is the value for which you are calculating the z-score.
- μ is the mean of the data set.
- σ is the standard deviation of the data set.
By substituting the appropriate values into the formula, you can determine how far a value is from the mean in terms of standard deviations. A positive z-score indicates the value is above the mean, while a negative z-score means it is below the mean. Z-scores of 0 represent values that are exactly at the mean.
Once you calculate the z-score, it can be used to determine probabilities or percentiles within a dataset, helping to make data-driven decisions or predictions. This process is fundamental when working with statistical models or interpreting complex data sets.
Normal Distribution and Probability
Understanding the connection between statistical models and the likelihood of different outcomes is essential for making accurate predictions. These models help visualize how data points are spread across a range, allowing you to calculate the probability of specific events. By examining the shape and spread of the curve, you can assess how likely it is for a value to fall within a certain interval. This insight is crucial for interpreting data in a meaningful way.
One of the most important aspects of probability in this context is calculating the area under the curve. The area represents the likelihood of an event occurring within a given range. This is where z-scores come into play, as they help determine the specific probability associated with different segments of the curve.
| Z-Score Range | Probability |
|---|---|
| -1 to 1 | 68.27% |
| -2 to 2 | 95.45% |
| -3 to 3 | 99.73% |
In this table, the z-scores represent the standard deviations from the mean, and the associated probabilities show the likelihood of values falling within those ranges. By understanding this, you can calculate the probability of outcomes occurring within specific intervals, making informed decisions based on statistical data.
Common Mistakes in Normal Distribution Problems

When working with problems related to statistical models, it’s easy to make errors that can lead to incorrect conclusions. Many of these mistakes stem from misinterpreting key concepts or applying formulas incorrectly. Being aware of the most common pitfalls can help you approach problems more effectively and avoid errors that affect the accuracy of your results.
Misunderstanding the Z-Score Calculation
One frequent mistake is incorrectly calculating the z-score. Remember, the z-score formula requires you to subtract the mean from the data point and then divide by the standard deviation. Forgetting to divide by the standard deviation or mixing up the numerator and denominator can lead to miscalculations. It’s crucial to double-check each step in the formula to ensure accuracy.
Confusing Probability and Percentages
Another common error is mixing up probabilities with percentages. When interpreting the area under the curve, it’s important to remember that probability is expressed as a decimal, not a percentage. For example, 68% should be written as 0.68 when performing calculations. This confusion can lead to significant misinterpretation of the data.
Incorrect Use of Tables
Using standard tables incorrectly is another issue. These tables typically give the cumulative probability up to a certain z-score, but many students mistakenly assume the tables provide the total probability from one z-score to another. Always ensure you’re interpreting the correct part of the table–whether it’s the probability up to a value or between two values–before making your final calculation.
Overlooking the Symmetry
Since many statistical models are symmetric, overlooking this symmetry can lead to errors in calculations. For example, if you’re asked to find the probability of a value being less than a certain number, but you accidentally calculate it for the opposite side, your result will be incorrect. Always keep in mind that data on one side of the mean mirrors that on the other side.
By understanding these common errors and carefully reviewing your work, you can significantly reduce mistakes and improve your accuracy when solving problems related to statistical models.
Interpreting Normal Distribution Tables
Statistical tables are essential tools for working with probability models. They provide the cumulative probability associated with specific values, helping you determine how likely certain outcomes are. Understanding how to read and interpret these tables is critical for solving problems accurately. Incorrectly using the tables can lead to erroneous conclusions, so it’s important to follow a systematic approach when referencing them.
Key Components of the Tables
Most standard statistical tables provide the cumulative probability for various z-scores, which represent the number of standard deviations a value is from the mean. Here’s how to interpret the information:
- Rows: The rows typically represent the first two digits of the z-score (the whole number and the first decimal point). For example, a row for “1.2” would show the probabilities for all values between 1.2 and 1.29.
- Columns: The columns usually show the second decimal point of the z-score. For instance, a column for “.08” would represent the values of z-scores from 1.20 to 1.28.
- Values: The values in the body of the table show the cumulative probability up to that z-score. This represents the area under the curve from the far left up to the z-score.
How to Use the Tables

To use the table, you first need to calculate the z-score for the value you’re interested in. Once you have the z-score, find the corresponding row and column in the table:
- Calculate the z-score using the formula: Z = (X – μ) / σ.
- Locate the row corresponding to the first two digits of the z-score.
- Find the column that matches the second decimal place.
- Find the intersection of the row and column to obtain the cumulative probability.
For example, if you calculated a z-score of 1.25, you would find the row for 1.2 and the column for 0.05. The value at the intersection would give you the cumulative probability up to that z-score.
Once you understand how to use these tables, you can accurately assess probabilities and make more informed decisions based on your data.
Using the Empirical Rule for Quick Estimations
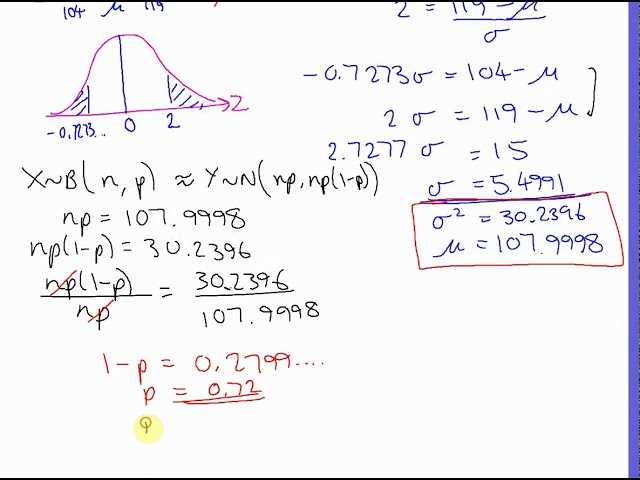
The empirical rule offers a quick way to estimate probabilities and data spread without needing to perform detailed calculations. This rule applies to datasets that follow a specific type of statistical pattern, helping to provide approximate insights into the likelihood of certain outcomes. By understanding the rule, you can make rapid judgments about how values are distributed around the central point, saving time and effort in your analysis.
The rule states that for a typical dataset, the majority of values lie within a certain number of standard deviations from the mean. This allows for quick estimations of data spread and probability ranges without requiring complex computations.
| Standard Deviations from Mean | Percentage of Data |
|---|---|
| 1 | 68% |
| 2 | 95% |
| 3 | 99.7% |
As shown in the table, approximately 68% of values fall within one standard deviation from the mean, 95% within two, and nearly 99.7% within three. This rule helps to quickly assess the spread of data, estimate the probability of a value falling within a specific range, and make predictions based on this information.
By applying the empirical rule, you can efficiently interpret data, make rapid assessments of probability, and avoid the need for time-consuming calculations in many scenarios.
Real-Life Applications of Normal Distribution
Statistical models play a crucial role in understanding and predicting real-world phenomena. They are applied across various fields, helping professionals make informed decisions based on data patterns. In many cases, these models allow for efficient predictions and estimations, simplifying complex processes in industries ranging from healthcare to finance. Here are some common areas where these models are put to use:
- Quality Control in Manufacturing
Companies use statistical models to monitor product consistency. By understanding the variation in measurements, manufacturers can ensure products meet quality standards and quickly identify defects. - Healthcare and Medical Research
In healthcare, these models help assess the spread of certain traits or conditions within populations. For example, doctors may use data on the average height, weight, or blood pressure of a group of people to identify any outliers and ensure treatments are effective. - Finance and Stock Market Analysis
Investors rely on statistical models to predict stock performance and assess risk. By analyzing past performance data, financial analysts can forecast potential returns and make informed investment decisions. - Education and Standardized Testing
Educational institutions use these models to analyze test scores and evaluate student performance. This helps in comparing students’ results to broader standards, allowing for adjustments in teaching strategies. - Sports Performance Analysis
Coaches and analysts often use statistical models to assess players’ performance and predict outcomes. This approach helps in identifying strengths, weaknesses, and areas for improvement.
These examples highlight how statistical models are integral to various industries, enabling professionals to make data-driven decisions and improve outcomes. By using data to uncover patterns, businesses, healthcare providers, and analysts can optimize performance, reduce risk, and drive growth.
Critical Values in Normal Distribution
In statistical analysis, critical values are key thresholds used to determine the significance of observed data. These values help professionals assess whether a particular result falls within a certain probability range or if it is unusual enough to warrant further investigation. Critical values are particularly useful in hypothesis testing, where they act as a decision-making tool to reject or fail to reject a hypothesis.
Understanding Critical Values
Critical values are typically associated with specific confidence levels and are derived from statistical tables or calculated using software tools. They represent the boundary points beyond which the probability of an event occurring is extremely low. Here’s how they are applied:
- Hypothesis Testing: Critical values are used to compare a test statistic against a threshold to decide whether the null hypothesis should be rejected or not.
- Confidence Intervals: They help in determining the range within which the true population parameter is likely to fall, based on the sample data.
- Outlier Detection: By using critical values, one can identify data points that deviate significantly from the mean and are considered outliers.
Common Critical Values
Critical values vary depending on the confidence level and the type of test being conducted. Below are some common critical values for a standard 95% confidence level (two-tailed test):
- 1.96: This value is used for a 95% confidence level in a two-tailed test. It marks the point beyond which 5% of values lie outside the central area of the curve.
- 2.58: For a 99% confidence level, the critical value increases, indicating that a wider range of values is required to ensure high confidence in the results.
- 1.64: Used for a 90% confidence level, indicating that the critical region is narrower compared to higher confidence levels.
These critical values help guide statistical decision-making, providing thresholds that aid in the interpretation of data and results. They are vital in ensuring that conclusions drawn from data are reliable and backed by statistical evidence.
Differences Between Normal and Skewed Distributions
In statistical analysis, understanding the shape and characteristics of a dataset is essential for proper interpretation. Two common types of data patterns are symmetrical distributions and those that are skewed in one direction. The key distinction between these two lies in how the values are spread relative to the central tendency of the dataset. Recognizing these differences is crucial when selecting appropriate statistical methods and drawing meaningful conclusions from data.
A symmetrical distribution is evenly spread around the center, while a skewed pattern indicates that the data is not balanced and leans more toward one side. This difference in shape affects how data is analyzed, how outliers are handled, and what conclusions can be drawn from the dataset.
| Characteristic | Symmetrical Distribution | Skewed Distribution |
|---|---|---|
| Shape | Bell-shaped curve with equal tails | Uneven tails, data is stretched on one side |
| Central Tendency | Mean, median, and mode are the same | Mean is pulled towards the longer tail |
| Outliers | Symmetrically distributed | More extreme values in one direction |
| Common Examples | Heights, weights, test scores | Income distribution, age at retirement |
As shown in the table, a symmetrical pattern is balanced with its tails on either side of the central value, while skewed data has one longer tail, indicating an imbalance. The presence of skewness impacts various statistical measures and makes it important to choose appropriate tools for analysis. Recognizing these differences helps ensure accurate data interpretation and better decision-making in both research and practical applications.
Understanding the 68-95-99.7 Rule
The 68-95-99.7 rule is a statistical principle that describes how data is spread around the central value in a typical pattern. This rule provides a quick and useful way to estimate the percentage of data that falls within certain ranges of the mean. It is based on the idea that data points near the center are more likely to occur than those farther away, with the frequency of occurrences decreasing as the data moves further from the center.
According to this rule, data in a symmetric pattern is distributed in such a way that specific percentages of values fall within certain intervals from the central value:
- 68%: About 68% of all values fall within one standard deviation from the mean.
- 95%: Around 95% of the data points fall within two standard deviations of the mean.
- 99.7%: Almost all values, approximately 99.7%, lie within three standard deviations from the mean.
This rule is valuable for understanding the spread of data in many fields, as it allows for a quick estimation of how much of the data lies within a given range. It helps in identifying patterns, assessing variability, and making predictions based on observed trends. Whether used in scientific research, business analysis, or everyday applications, the 68-95-99.7 rule provides a simple framework for understanding how data behaves in a predictable and consistent manner.
Normal Distribution in Statistical Inference
In statistical analysis, drawing conclusions about a population based on sample data is a key objective. This process, known as statistical inference, involves making predictions or generalizations from a subset of data. A common assumption in many statistical methods is that the data follows a specific pattern, which allows for the application of certain tests and confidence intervals. This concept plays a vital role in hypothesis testing, confidence estimation, and predictive modeling.
One of the primary tools in statistical inference is the use of a symmetric pattern where data points are concentrated around the central value. By assuming this pattern, statisticians can make more accurate predictions and assessments regarding the population parameters. The principles governing this pattern help determine the likelihood of various outcomes, which is crucial for informed decision-making.
- Hypothesis Testing: Statistical tests such as z-tests and t-tests rely on the assumption that the data follows a predictable pattern to determine the probability of a hypothesis being true.
- Confidence Intervals: By using the assumed pattern, statisticians can estimate a range of values within which the population parameter is likely to fall, with a certain level of confidence.
- Sampling Distribution: Understanding how sample statistics behave when drawn from a population is crucial for making inferences. The assumed pattern allows for the use of tools like the Central Limit Theorem to make reliable estimates.
Statistical inference tools that utilize these assumptions provide a way to quantify uncertainty and draw meaningful conclusions from data. Whether you’re estimating means, testing hypotheses, or calculating confidence intervals, understanding the shape and behavior of the data is essential for accurate analysis and decision-making.
How to Solve Z-Score Problems
In statistical analysis, one common task is to standardize data so that it can be compared across different sets or contexts. This process involves calculating a value that reflects how far a specific data point is from the mean, in terms of standard deviations. By understanding this measure, analysts can assess how unusual or typical a given value is within a dataset.
To solve problems involving this measure, the process is straightforward but requires understanding key components. The formula for calculating the value involves subtracting the mean from the observed data point and then dividing the result by the standard deviation. This gives a standardized value, which can be interpreted to assess the relative position of the data point.
The formula is:
z = (X - μ) / σWhere:
- z: The standardized value or z-score.
- X: The observed data point.
- μ: The mean of the dataset.
- σ: The standard deviation of the dataset.
To apply this formula, follow these steps:
- Step 1: Determine the observed data point (X), the mean (μ), and the standard deviation (σ) from the given information.
- Step 2: Subtract the mean from the observed data point to find the difference.
- Step 3: Divide the result by the standard deviation to obtain the standardized value (z).
Once the z-score is calculated, it can be interpreted using tables or statistical software to determine the probability of the data point occurring within the dataset. A higher absolute z-score indicates that the data point is farther from the mean, suggesting it is more extreme. Conversely, a z-score closer to zero means the data point is near the mean, indicating typical behavior within the dataset.
Calculating Probabilities in Normal Distribution
In statistical analysis, understanding the likelihood of a certain event or value occurring within a dataset is essential for making informed predictions. This concept is particularly useful when working with data that follows a symmetric pattern, where values tend to cluster around a central point. By calculating the probability, you can assess how common or rare a particular outcome is relative to the dataset as a whole.
To calculate probabilities, the first step is to standardize the data using a measure that indicates how far a specific data point is from the average, typically expressed in terms of standard deviations. Once the data point is standardized, you can refer to a standard table or use statistical software to find the corresponding probability for that value.
Here’s how to calculate probabilities:
- Step 1: Identify the data point, the mean, and the standard deviation from the given dataset.
- Step 2: Standardize the data point by subtracting the mean from the value and dividing the result by the standard deviation to obtain the standardized value (z-score).
- Step 3: Use a statistical table or calculator to find the probability associated with the calculated z-score.
Once you have the z-score, it represents the area under the curve to the left of the data point. This area corresponds to the probability of observing a value less than or equal to the given data point. If you are interested in the probability of a value greater than the observed point, you can subtract the area from 1, as the total area under the curve always sums to 1.
By mastering this process, you can effectively calculate the likelihood of a variety of outcomes and apply this knowledge to make informed decisions, estimate risks, or predict future events based on statistical data.
Visualizing Normal Distribution with Graphs
In statistical analysis, visual representation is crucial for understanding data patterns and drawing meaningful conclusions. Graphs allow you to quickly see the overall shape, central tendency, and spread of a dataset. One of the most effective ways to illustrate the behavior of data is through bell-shaped curves, which show how values are distributed across different ranges.
By plotting data points on a graph, you can visually assess how they cluster around a central point, providing insight into the frequency and likelihood of specific values. This visualization helps in determining the spread, peak, and symmetry of the data, making it easier to identify outliers or unusual trends.
There are several key elements to focus on when creating a graph for this type of data:
- Central peak: This represents the mean, or the point where most data points are concentrated.
- Symmetry: The curve is typically symmetric, meaning it has a mirror image on either side of the central point.
- Spread: The width of the curve shows how dispersed the data is around the mean, often represented by standard deviations.
- Tails: The ends of the curve show the less frequent, extreme values that fall far from the mean.
To help with visualizing these concepts, here’s a table that shows how the percentage of values typically falls within certain ranges in a bell-shaped curve:
| Standard Deviations from the Mean | Percentage of Data |
|---|---|
| ±1 | 68% |
| ±2 | 95% |
| ±3 | 99.7% |
These values indicate the proportion of data that falls within each range of standard deviations from the central point. For example, about 68% of the data will lie within one standard deviation of the mean, while 95% will fall within two standard deviations.
By using graphs and understanding these key principles, you can gain deeper insights into your data and make more informed statistical decisions based on the visual patterns observed in the graph.
Tips for Tackling Normal Distribution Exam Questions
Approaching problems related to data patterns can be challenging, but with the right strategy, you can improve your efficiency and accuracy. Understanding key concepts, such as central tendency, variability, and probability, is crucial for solving these types of problems effectively. By mastering essential techniques, you can navigate through calculations and interpretations with confidence.
1. Understand the Basic Concepts
Before diving into the specifics of the problem, ensure that you understand the core principles that govern the data. Familiarize yourself with terms like mean, standard deviation, and how data tends to cluster around the central value. Recognizing the shape of the curve and the role of the mean can help in interpreting the data correctly.
2. Practice with Standard Z-Scores
Z-scores are fundamental for comparing individual data points to the overall dataset. Practice calculating z-scores for different data points to better understand their relative position. This will help you quickly determine how a particular value compares to the entire dataset and is often a critical step in solving problems.
3. Break Down the Problem Step by Step
Avoid rushing into the solution. Instead, take a methodical approach. Break the problem into smaller, manageable parts. First, identify the given information, then determine what is being asked, and finally apply the appropriate formulas to solve for the unknowns. This approach helps in avoiding unnecessary mistakes.
4. Use Visual Aids When Possible
Whenever possible, draw out a simple graph to visualize the problem. Plotting the data on a curve can help you better understand the relationships between the values and provide a clearer picture of how the data behaves. Visual aids can also serve as a reference when calculating areas or percentages under the curve.
5. Familiarize Yourself with the Empirical Rule
The empirical rule can be a powerful tool when solving problems that involve probabilities and data spread. Remember that about 68%, 95%, and 99.7% of the data will fall within 1, 2, and 3 standard deviations from the mean, respectively. This rule can help you quickly estimate probabilities without needing complex calculations.
6. Pay Attention to the Units
Ensure that all measurements are in the same units before performing calculations. Converting units when necessary can prevent errors in your answers and provide more accurate results. Always double-check that your final answer is consistent with the units in the problem.
7. Review Common Mistakes
Familiarize yourself with common pitfalls, such as misinterpreting z-scores or incorrectly using the empirical rule. Understanding the areas where students tend to make mistakes will help you avoid those errors and approach problems with greater precision.
By applying these strategies, you can approach problems related to data patterns with a clear mindset and solve them effectively. Regular practice and familiarity with the key concepts will allow you to handle more complex problems with ease, leading to better performance in your assessments.