
In this section, we explore advanced topics that build on previous knowledge and provide a deeper understanding of mathematical problem-solving. These concepts often challenge students to apply a range of skills and strategies to solve complex problems, requiring a solid foundation in fundamental principles.
With a focus on mastering equations, functions, and their graphical representations, this guide helps clarify the essential techniques and solutions you’ll need. By breaking down difficult problems into manageable steps, you can confidently approach each type of question and gain a clearer understanding of the material.
In this resource, we provide detailed explanations and methods to help students navigate through tricky problems. Whether you’re revisiting familiar topics or encountering new challenges, this guide serves as a comprehensive tool for mastering the material.
Mathematical Solutions and Methods for Section 6

This section provides a comprehensive breakdown of the essential problem-solving strategies for the more advanced concepts introduced earlier. By exploring various mathematical methods and their practical applications, it offers an opportunity to solidify your understanding and test your skills.
Each solution is carefully explained to highlight the step-by-step process needed to tackle these types of questions. Whether you’re solving complex equations or analyzing functions, the solutions are presented clearly to ensure easy comprehension and application of the techniques.
Understanding the reasoning behind each solution is key to mastering the material. This guide serves as a valuable resource for those looking to deepen their knowledge and improve their problem-solving abilities in this area of mathematics.
Key Concepts Covered in Section 6
This section delves into the core principles that are fundamental for mastering advanced mathematical techniques. The topics addressed here build on earlier material and introduce more complex problems, challenging students to apply a broader range of methods.
The primary focus is on equations, functions, and their interrelationships, with an emphasis on problem-solving strategies and real-world applications. By understanding these central ideas, students can develop a stronger grasp of the material and confidently tackle more intricate tasks.
| Concept | Description |
|---|---|
| Quadratic Equations | Techniques for solving and graphing quadratic equations. |
| Function Properties | Analyzing and understanding the behavior of different types of functions. |
| Radical Expressions | Methods for simplifying and solving radical equations. |
| Systems of Equations | Solving systems using substitution, elimination, and graphical methods. |
| Polynomial Operations | Techniques for factoring and solving polynomial equations. |
How to Approach Mathematical Problems
When facing complex mathematical problems, it’s essential to break them down into smaller, more manageable steps. Approaching each problem with a clear strategy can help reduce confusion and ensure that all aspects are addressed systematically. Whether you’re solving equations, analyzing graphs, or working with functions, a step-by-step process will guide you through to the correct solution.
Step 1: Understand the Problem
Before diving into calculations, take a moment to fully understand the question. Identify key information, such as the type of equation or function involved, and determine what is being asked. This helps set the direction for your approach.
Step 2: Organize Your Work
Write down all known variables, formulas, or relationships. This visual organization can make the problem easier to follow and ensures no crucial steps are missed. Clear, organized work leads to more accurate solutions.
Patience and practice are key when tackling advanced mathematical problems. With each new challenge, applying these techniques will become more intuitive, helping you solve problems efficiently and correctly.
Step-by-Step Solutions for Section 6

In this section, we will break down each problem into clear, manageable steps, providing detailed explanations for every solution. By following these steps, you will be able to approach complex tasks with confidence and ensure accuracy in your work. Each problem is tackled using a logical sequence, ensuring that no critical detail is overlooked.
With each solution, we focus on the core techniques and strategies that are most effective for solving the types of problems covered in this section. By understanding the reasoning behind each step, you will not only arrive at the correct answer but also develop a deeper understanding of the underlying concepts.
Understanding Quadratic Equations in Detail
Quadratic equations are a foundational concept in mathematics that involve polynomial expressions with a degree of two. These equations are commonly encountered in various problem-solving scenarios, from graphing to real-world applications. Understanding how to solve and interpret these types of problems is crucial for advancing in more complex mathematical topics.
To fully grasp quadratic equations, it’s essential to explore the different methods for solving them, such as factoring, completing the square, and using the quadratic formula. Each approach offers unique advantages depending on the structure of the equation. Additionally, interpreting the solutions within the context of the problem can provide valuable insights into the behavior of functions represented by these equations.
Common Mistakes in Section 6 and How to Avoid Them
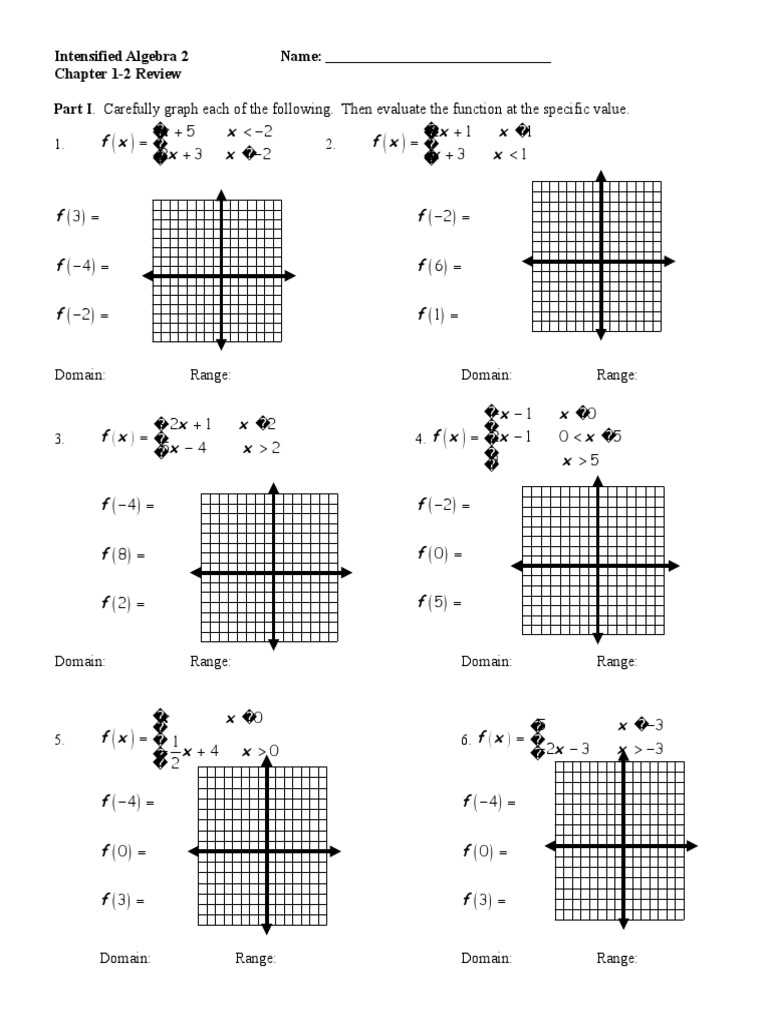
When working through more complex mathematical problems, it’s easy to overlook key details or make simple mistakes that can affect the outcome. Identifying and understanding these common errors is essential for improving problem-solving accuracy. This section highlights the most frequent issues students encounter and provides strategies to avoid them.
Misunderstanding Problem Requirements
One of the most common mistakes is misinterpreting what the problem is asking. Always take the time to read through the problem carefully and highlight the important information. Here are some key points to avoid confusion:
- Ensure you understand what is being solved for.
- Look for specific instructions, such as whether the answer should be in a simplified or factored form.
- Pay attention to negative signs and terms that may be easily overlooked.
Errors in Applying Formulas
Another common mistake is misapplying formulas or forgetting crucial steps in the process. To avoid this:
- Always write down the formula before you begin solving.
- Check that all terms are correctly substituted into the formula.
- Review the order of operations to ensure you’re following the correct sequence.
By being mindful of these typical errors and implementing the suggested strategies, you can improve your accuracy and efficiency in solving mathematical problems in this section.
Graphing Techniques for Section 6
Graphing is a powerful tool for visualizing mathematical relationships and understanding the behavior of different types of functions. In this section, we explore the various techniques that can help you accurately plot equations and interpret their graphical representations. Mastering these techniques allows for a deeper understanding of how equations behave in real-world scenarios.
One key approach to graphing is identifying the key features of the equation, such as intercepts, vertices, and asymptotes, before plotting the points on a coordinate plane. By focusing on these key elements, you can create a more accurate graph that reflects the true nature of the function.
Additionally, using graphing tools such as plotting software or graphing calculators can help speed up the process and offer visual confirmation of your results. Understanding the significance of the graph’s shape and direction can also provide insight into the solutions and behavior of the equation itself.
Exploring Functions and Their Properties
In this section, we focus on understanding the essential characteristics of functions and how to analyze their behavior. Functions are mathematical relationships that map inputs to outputs, and knowing their properties helps in solving a wide range of problems. By exploring the key aspects such as domain, range, and continuity, you can develop a deeper insight into how these functions behave in various scenarios.
Key Properties of Functions
Every function has specific properties that define its shape and behavior. Some of the most important properties include:
- Domain: The set of all possible input values for the function.
- Range: The set of all possible output values.
- Continuity: Whether the function is unbroken over its domain.
Graphical Interpretation of Functions
Graphing a function provides a visual representation that can help in understanding its behavior. The graph allows you to observe key features such as intercepts, slopes, and asymptotes. By analyzing these visual cues, you can make predictions about the function’s values and its overall behavior under different conditions.
Factoring Strategies for Polynomials
Factoring is an essential technique for simplifying polynomial expressions and solving equations. By breaking down polynomials into their simplest components, you can solve problems more efficiently and understand their underlying structure. In this section, we explore various factoring strategies that can be applied to different types of polynomial expressions.
Common Factoring Methods
There are several key strategies to factor polynomials effectively:
- Factoring out the greatest common factor (GCF): Begin by identifying the highest common factor of all terms in the polynomial and factoring it out.
- Factoring by grouping: For polynomials with four or more terms, grouping terms in pairs can make it easier to factor by recognizing common factors in each group.
- Difference of squares: Recognize expressions of the form a² – b², which can be factored as (a + b)(a – b).
Special Polynomial Forms
Certain polynomials follow specific patterns that make them easier to factor. Some common examples include:
- Perfect square trinomials: These can be factored as (a + b)² or (a – b)².
- Sum and difference of cubes: Polynomials of the form a³ + b³ or a³ – b³ can be factored using special formulas.
Mastering these techniques allows you to simplify complex expressions and solve equations more efficiently, providing the foundation for solving more advanced mathematical problems.
Solving Radical Equations and Expressions
Radical equations and expressions involve roots, such as square roots, cube roots, and higher-order roots, which are essential to solving a variety of problems. These equations can often seem challenging, but with the right approach, they can be simplified and solved systematically. In this section, we will discuss strategies for solving these equations and simplifying the expressions containing radicals.
When solving radical equations, the first step is typically to isolate the radical on one side of the equation. Once this is done, the next step is to eliminate the radical by raising both sides of the equation to the appropriate power. After simplifying the equation, it’s important to check for extraneous solutions that may arise from squaring both sides or manipulating the equation in other ways.
Steps to Solve Radical Equations
- Isolate the radical expression on one side of the equation.
- Raise both sides of the equation to the power that eliminates the radical.
- Simplify the resulting equation and solve for the variable.
- Check for extraneous solutions by substituting the solutions back into the original equation.
Example Problem

Consider the equation √(x + 3) = 5. To solve this equation, follow these steps:
| Step 1: | Square both sides: (√(x + 3))² = 5² |
| Step 2: | x + 3 = 25 |
| Step 3: | x = 25 – 3 |
| Step 4: | x = 22 |
After solving for x, substitute x = 22 back into the original equation to verify that it satisfies the equation. This ensures that no extraneous solutions are present.
Tips for Effective Study and Practice
Mastering mathematical concepts requires both consistent practice and a strategic approach to studying. By organizing your study sessions and using targeted techniques, you can improve your understanding and problem-solving skills. This section outlines some key tips for effective study and practice that can help you achieve better results and deepen your comprehension of complex topics.
Structured Study Habits
Creating a structured study routine is essential for staying on track and making the most out of each session. Consider the following approaches:
- Set clear goals: Define what you want to achieve in each session, whether it’s mastering a specific concept or solving a set number of problems.
- Break down tasks: Tackle one concept at a time and break large tasks into smaller, manageable steps to avoid feeling overwhelmed.
- Use spaced repetition: Review material regularly over increasing intervals to reinforce your understanding and improve retention.
Active Practice and Review

Active practice is crucial for reinforcing theoretical knowledge and ensuring that you can apply concepts correctly. These strategies can enhance your practice sessions:
- Solve a variety of problems: Work through a range of problems, including different types and difficulty levels, to build a deeper understanding.
- Work through mistakes: When you make errors, don’t just move on. Understand why you made the mistake and how to avoid it in the future.
- Use online resources: Supplement your learning with online tutorials, videos, and interactive practice problems for additional explanations and examples.
By following these tips and maintaining a disciplined, focused approach to studying, you’ll be able to improve your skills and gain more confidence in solving mathematical challenges.
Reviewing Key Theorems and Formulas
In mathematical problem-solving, understanding and applying fundamental theorems and formulas is essential for simplifying complex expressions and equations. This section focuses on some of the most important principles that can guide you through various problems. By familiarizing yourself with these key concepts, you will be able to approach challenges with confidence and efficiency.
Important Theorems to Remember
Below are some of the core theorems that are frequently used in solving equations and simplifying expressions:
- Pythagorean Theorem: Relates the lengths of the sides of a right triangle: a² + b² = c², where c is the hypotenuse.
- Quadratic Formula: Used to solve quadratic equations: x = (-b ± √(b² – 4ac)) / 2a.
- Zero Product Property: If the product of two numbers is zero, at least one of the numbers must be zero.
Essential Formulas to Master

Formulas are key tools in solving a wide range of mathematical problems. Below is a selection of important formulas you should know:
- Distance Formula: Used to calculate the distance between two points: d = √((x₂ – x₁)² + (y₂ – y₁)²).
- Slope Formula: Used to find the slope between two points: m = (y₂ – y₁) / (x₂ – x₁).
- Area of a Triangle: Area = ½ * base * height.
- Compound Interest Formula: A = P(1 + r/n)^(nt), where A is the amount, P is the principal, r is the rate, n is the number of times interest is compounded per year, and t is time in years.
By mastering these theorems and formulas, you’ll be well-equipped to approach a variety of mathematical problems and gain a deeper understanding of the relationships between numbers and expressions.
How to Check Your Work in Algebra 2
Ensuring the accuracy of your calculations and solutions is crucial when solving mathematical problems. Verifying your work allows you to identify errors early and understand the steps involved in reaching the correct solution. In this section, we’ll explore effective strategies to check your solutions and improve your problem-solving skills.
Step-by-Step Verification Methods
One of the most reliable ways to check your work is by retracing your steps. Follow these methods to confirm your results:
- Substitute Back into the Original Equation: After solving for the variable, substitute your solution back into the original problem to ensure both sides of the equation are equal.
- Check for Consistency: If working with a system of equations, check that the solutions satisfy all the equations simultaneously.
- Use Approximation: For complex calculations, estimate the expected result before solving. This can help you identify if your answer is in the correct range.
Common Tools for Error Checking
There are various tools and techniques that can help you spot mistakes:
- Graphing: For equations involving functions, graphing the solutions can give a visual representation of whether your results make sense.
- Double-Check Operations: Carefully review each step of your operations, particularly when dealing with fractions, exponents, or negative signs.
- Use a Calculator: For verification, you can use a calculator to check intermediate steps, but always understand the process behind the solution.
By developing a routine of checking your work and practicing error-detection strategies, you can build confidence in your solutions and reduce mistakes over time.
Real-World Applications of Algebra 2 Concepts
The concepts learned in this level of mathematics are not just abstract ideas; they have real-world applications that impact many fields, from engineering to economics. Understanding how to use mathematical principles effectively can help solve practical problems in various industries. In this section, we will explore some of the ways these concepts are used outside the classroom.
Applications in Engineering and Technology
Mathematics plays a central role in engineering and technology. From designing structures to creating software, the principles learned in this course help professionals solve complex problems:
- Structural Engineering: The design and analysis of buildings and bridges require solving systems of equations to ensure structural integrity and safety.
- Computer Programming: Algorithms and data processing often involve mathematical models to optimize performance, such as sorting algorithms and encryption techniques.
- Electrical Engineering: Understanding exponential functions and complex numbers is crucial for designing circuits and analyzing signal processing.
Applications in Business and Economics
Mathematics is also widely used in business and economics for decision-making and strategic planning. Here are some examples of how these concepts are applied:
- Cost Analysis: Businesses use systems of equations to determine the optimal pricing for products based on cost structures and market demand.
- Investment Strategies: Compound interest and exponential growth formulas are used to predict investment returns and evaluate financial risk.
- Market Trends: Linear and quadratic models help economists and analysts predict market behavior and identify potential business opportunities.
As you continue to study and apply these concepts, remember that their relevance stretches far beyond the classroom and can lead to exciting opportunities in a variety of fields.
Preparing for Algebra 2 Exams and Tests
Effective preparation for exams and tests involves more than just reviewing concepts. It requires understanding the material, practicing problem-solving techniques, and identifying areas that need improvement. In this section, we will discuss strategies to help you succeed in your upcoming assessments.
Review Key Concepts and Formulas

Start by revisiting the essential concepts and formulas that are frequently tested. Focus on the areas where you feel least confident, and make sure you understand the underlying principles. Consider creating a summary sheet of important formulas, theorems, and methods for quick reference. This will help reinforce your memory and make it easier to apply these concepts during the test.
Practice Problem-Solving
The best way to prepare for any math test is by practicing a variety of problems. Work through practice questions that cover different topics, ensuring you get comfortable with various problem types. Time yourself to simulate the test environment and improve your speed. If you encounter difficulties, don’t just skip over them–take the time to understand the solution process and clarify any doubts.
In addition to working on individual problems, consider reviewing previous assignments and quizzes to identify any recurring patterns or mistakes. Addressing these issues beforehand can give you an advantage when it comes time for the exam.
Finally, ensure you take care of yourself physically and mentally. Get enough rest, stay hydrated, and avoid cramming at the last minute. A balanced approach will help you approach the exam with confidence and perform at your best.