In this section, we delve into fundamental mathematical principles designed to build a strong foundation for solving complex problems. The focus is on developing critical thinking and problem-solving strategies that can be applied across various topics.
Each problem presents a unique challenge, encouraging you to explore different methods for reaching solutions. By breaking down the tasks into manageable steps, you’ll gain a clearer understanding of how to approach and solve similar questions in the future.
Whether you’re reviewing foundational ideas or tackling more advanced concepts, this section provides essential techniques to enhance your skills and boost your confidence in mathematics.
Core Connections Geometry Chapter 1 Solutions
This section provides detailed solutions to foundational mathematical problems that explore the basic concepts of shapes, angles, and relationships. By analyzing and solving these exercises, you’ll strengthen your ability to approach more complex tasks with confidence.
The exercises in this section are designed to guide you through step-by-step problem-solving processes, making it easier to understand and apply essential principles. Each solution is explained in a way that highlights the reasoning behind each step, ensuring clarity and better comprehension.
Through these solutions, you’ll develop a deeper understanding of key techniques used to tackle similar questions. Whether you’re preparing for exams or simply looking to reinforce your knowledge, this guide will serve as an invaluable resource to improve your mathematical skills.
Understanding Basic Geometric Concepts
In this section, we explore the fundamental principles that form the foundation of spatial reasoning. These concepts are essential for analyzing the relationships between different shapes and understanding how they interact in various contexts.
Familiarizing yourself with these basics will help you develop the skills needed to tackle more complex problems. Key ideas such as points, lines, and angles serve as building blocks for more advanced topics and are crucial for interpreting diagrams and solving real-world challenges.
By mastering these essential concepts, you’ll be better equipped to approach mathematical problems with a deeper understanding of their structure and logic, making it easier to find solutions and apply them effectively.
Key Topics in Chapter 1 Mathematics
This section focuses on the fundamental topics that provide a solid foundation for further study in mathematical reasoning. By understanding the core ideas explored here, you will be able to grasp more advanced concepts and solve increasingly complex problems.
Among the key areas covered are basic shapes, measurements, and spatial relationships. These topics are essential for analyzing how different elements fit together and interact in various mathematical scenarios. A thorough understanding of these concepts is crucial for building strong problem-solving skills.
Additionally, we explore various techniques for simplifying problems, making it easier to find solutions while ensuring a deeper understanding of the material. Mastering these foundational ideas prepares you for tackling more challenging subjects in the future.
Exploring Problem-Solving Techniques
Solving mathematical problems requires a strategic approach to break down complex tasks into manageable steps. By developing effective techniques, you can simplify the problem-solving process and gain a deeper understanding of the material.
One key method is to first analyze the problem and identify the given information. This allows you to choose the appropriate strategy for finding a solution. Some useful approaches include:
- Drawing diagrams: Visualizing the problem often makes it easier to understand relationships between different elements.
- Applying known formulas: Recognizing patterns and using formulas can speed up the problem-solving process.
- Breaking the problem into smaller parts: Dividing a large problem into simpler, smaller steps often leads to a more straightforward solution.
- Checking your work: Verifying your calculations and ensuring consistency is key to avoiding errors and confirming accuracy.
By practicing these techniques and exploring different strategies, you will be better equipped to approach any problem with confidence and efficiency. Mastery of these skills will not only help in solving current problems but also in tackling more complex challenges in the future.
How to Approach Mathematical Exercises
Approaching mathematical tasks effectively requires a systematic method to break down the problem and identify the best strategy for solving it. By following a structured process, you can avoid feeling overwhelmed and increase your chances of finding the correct solution.
Here are some key steps to follow when tackling problems:
- Understand the problem: Read the problem carefully, ensuring you comprehend the given information and the question being asked.
- Identify important details: Highlight key values, relationships, or conditions that will guide your solution.
- Plan your approach: Think about the best method or formula to apply. Decide if a diagram, calculation, or logical reasoning is required.
- Execute step-by-step: Solve the problem one step at a time, making sure to stay organized and clear with each calculation or conclusion.
- Review your solution: Double-check your work to ensure that each step makes sense and that your final answer is accurate.
By following these steps, you can approach exercises with greater confidence and improve your problem-solving skills. Practice will help refine your approach and develop a deeper understanding of the concepts involved.
Step-by-Step Solutions for Chapter 1
In this section, we will guide you through detailed, step-by-step solutions to the problems presented in the first section. These solutions will help you understand how to approach similar problems, breaking down each task into manageable steps for easier comprehension and application.
Solution 1: Basic Problem Breakdown
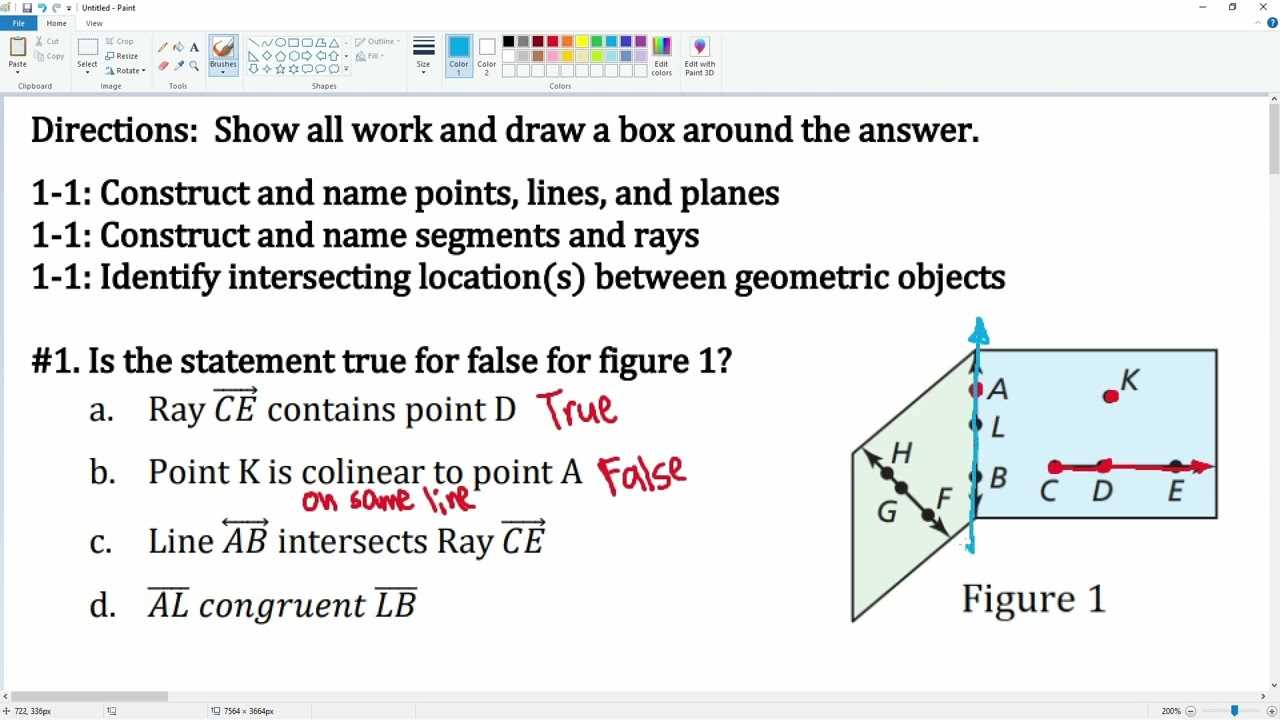
The first problem requires analyzing basic shapes and their properties. Here’s how you can solve it:
- Step 1: Read the problem carefully and identify the key elements, such as given values and unknowns.
- Step 2: Draw a diagram to visualize the relationships between the different parts of the problem.
- Step 3: Apply relevant principles or formulas to set up the solution.
- Step 4: Solve the equation or simplify the expressions as needed to find the final answer.
- Step 5: Double-check the solution to ensure accuracy and consistency with the problem’s requirements.
Solution 2: Applying Logical Reasoning
For the next exercise, logical reasoning is key to finding the solution. Here’s how to break it down:
- Step 1: Identify the geometric relationships or conditions given in the problem.
- Step 2: Use logical deductions to simplify the problem and uncover the necessary steps.
- Step 3: Work through the problem systematically, applying appropriate reasoning at each stage.
- Step 4: Solve for the unknowns, using algebraic or geometric techniques as necessary.
- Step 5: Verify your final answer against the conditions outlined in the problem.
By following these steps, you will gain a clearer understanding of how to approach and solve problems in this section, enhancing your problem-solving skills and mathematical reasoning.
Important Formulas for Success

To solve mathematical problems effectively, it’s crucial to understand and apply the right formulas. These formulas serve as tools to simplify complex tasks, providing a structured approach to finding solutions. Mastering key equations can greatly enhance your problem-solving abilities and increase your overall efficiency.
Basic Formulas for Solving Problems
The following table highlights some of the essential formulas commonly used in mathematical tasks involving shapes, measurements, and calculations.
| Formula | Application |
|---|---|
| Area of a Triangle | Area = 1/2 × base × height |
| Perimeter of a Rectangle | Perimeter = 2 × (length + width) |
| Area of a Circle | Area = π × radius² |
| Pythagorean Theorem | c² = a² + b² |
| Volume of a Cube | Volume = side³ |
Advanced Formulas for Complex Calculations
As you progress, more advanced formulas may be required to handle intricate problems involving various geometric properties. These include equations related to surface areas, volumes, and angles within more complex shapes.
By mastering both basic and advanced formulas, you will be better equipped to approach problems with confidence and precision, ensuring accurate solutions to even the most challenging questions.
Common Mistakes in Mathematical Problems
Even experienced problem solvers can make mistakes when tackling complex tasks. Recognizing these common errors and understanding how to avoid them is crucial for improving accuracy and efficiency. In this section, we explore frequent pitfalls that many encounter while solving mathematical problems and provide tips on how to overcome them.
Typical Errors in Problem Solving
The following list highlights some of the most common mistakes made during problem-solving:
- Misinterpreting the Problem: Failing to fully understand the question or overlooking key information can lead to incorrect approaches and solutions.
- Skipping Steps: Rushing through calculations or omitting intermediate steps may result in errors. Always work through the problem systematically.
- Incorrect Use of Formulas: Using the wrong formula for a given situation or misapplying a formula can lead to incorrect results.
- Failure to Double-Check: Not reviewing the solution after completing the problem can lead to overlooked mistakes or missed opportunities for simplification.
- Neglecting Units: Forgetting to include or convert units correctly can lead to incorrect answers, especially when dealing with measurements.
How to Avoid These Mistakes
To minimize these errors, it’s important to develop good habits:
- Take your time: Carefully read and analyze the problem before starting to solve it.
- Break down the problem: Work through the task step by step, ensuring you understand each part before proceeding.
- Review your work: Always double-check your calculations and the use of formulas to ensure everything is correct.
- Practice regularly: The more you practice, the more familiar you become with common challenges, which reduces the likelihood of making mistakes.
By being mindful of these common mistakes and actively working to avoid them, you’ll improve both the accuracy and efficiency of your problem-solving process, leading to better results overall.
Strategies for Mastering Mathematical Concepts
To truly excel in mathematical subjects, it’s important to adopt a structured approach to learning and practice. Mastering the core principles and methods involves not only understanding key concepts but also developing effective strategies that make solving problems easier and more intuitive. Below are some strategies that can help you build a strong foundation and enhance your skills.
1. Focus on Understanding Concepts
Rather than just memorizing formulas and procedures, take the time to understand the logic behind each concept. This deeper understanding will allow you to apply principles more flexibly and solve a wider range of problems.
- Ask Questions: Always seek clarification if something is unclear. Ask yourself why a formula works and how it can be applied in different scenarios.
- Connect Ideas: Try to see how different concepts relate to one another. Recognizing patterns across problems will make new challenges easier to approach.
2. Practice Regularly
Mathematical problem-solving is a skill that improves with practice. The more problems you work through, the more familiar you become with different types of questions and solutions.
- Start Simple: Begin with easier problems to build confidence and gradually progress to more challenging ones.
- Challenge Yourself: Don’t shy away from difficult problems. Tackling tougher questions will expand your problem-solving toolkit and improve your critical thinking abilities.
3. Break Down Complex Problems
When faced with a complex question, break it down into smaller, more manageable steps. This will help you focus on solving one part of the problem at a time, rather than feeling overwhelmed by the entire task.
- Identify Key Elements: Look for the given information and what needs to be found. This will guide your approach.
- Work Step-by-Step: Solve each part methodically, checking for errors as you go.
4. Use Visual Aids
Diagrams, graphs, and other visual tools can greatly enhance your understanding of mathematical problems, particularly when working with shapes and spatial reasoning. Drawing out problems can help you see relationships more clearly and simplify complex tasks.
- Draw Diagrams: Visualize the situation to get a better grasp of the problem.
- Label Key Information: Clearly mark important points, angles, and distances in your diagrams to avoid confusion.
5. Review and Reflect
After solving a problem, take the time to review your solution. Reflecting on the steps taken and identifying any mistakes will help reinforce your learning and prevent similar errors in the future.
- Double-Check Work: Review each step to ensure it makes sense and is mathematically sound.
- Learn from Mistakes: If you make an error, take note of it and understand why it occurred, so you can avoid it next time.
By employing these strategies consistently, you will develop a solid understanding of key mathematical principles and be better equipped to tackle any problem with confidence and precision.
Breaking Down Mathematical Problems
When approaching complex problems, it’s important to break them down into smaller, more manageable steps. This allows for a clearer understanding of the task and makes it easier to identify the right approach. In this section, we’ll discuss how to deconstruct problems systematically and apply logical methods to find solutions.
Step-by-Step Problem Breakdown
Breaking down a problem involves identifying key elements, understanding the relationships between them, and applying the correct techniques to solve each part. Here’s a simplified approach to tackling problems:
- Read and Understand: Carefully read through the problem to understand what is being asked. Pay attention to any given values and conditions.
- Identify Key Information: Highlight the essential pieces of information that are necessary to solve the problem.
- Choose the Right Approach: Decide on the best method to apply, whether it’s using formulas, drawing diagrams, or breaking the problem into sub-problems.
- Check for Simplifications: Look for ways to simplify the problem before proceeding with calculations, such as factoring or reducing fractions.
- Work Step-by-Step: Solve the problem gradually, ensuring each step is correct before moving on to the next one.
- Verify Results: After reaching a solution, review your steps and ensure the answer makes sense in the context of the problem.
Example Breakdown
Let’s look at an example problem to see how the breakdown process works in practice:
| Step | Action | Explanation |
|---|---|---|
| 1 | Read the Problem | Understand what is being asked and identify given values. |
| 2 | Identify Key Elements | Highlight important data points such as measurements, angles, or specific conditions. |
| 3 | Draw a Diagram | If necessary, visualize the problem using a diagram to help clarify relationships. |
| 4 | Apply the Right Formula | Use the appropriate formula based on the information provided. |
| 5 | Solve Step-by-Step | Work through the calculations carefully, checking each step as you go. |
| 6 | Verify the Solution | Double-check your answer to ensure it is reasonable and correct. |
By following this structured approach, you can confidently tackle even the most complex problems, ensuring that no step is overlooked and the solution is achieved systematically.
Vocabulary for Key Mathematical Concepts
Understanding the terminology used in mathematical problems is crucial for solving them efficiently. In this section, we will cover essential terms that are frequently used in the field of study. Knowing these definitions and how they relate to one another can provide a clearer path to solving various problems.
Here are some important terms that every learner should familiarize themselves with:
- Point: A precise location in space that has no dimensions, usually represented by a dot.
- Line: A straight one-dimensional figure that extends infinitely in both directions. It has length but no thickness.
- Angle: The space between two intersecting lines, measured in degrees. It indicates the rotation needed to bring one line into alignment with another.
- Plane: A flat, two-dimensional surface that extends infinitely in all directions. It contains an infinite number of points and lines.
- Segment: A part of a line that has two endpoints, defined by the distance between them.
- Ray: A portion of a line that has one fixed endpoint and extends infinitely in one direction.
- Perpendicular: When two lines or segments intersect to form right angles (90 degrees).
- Parallel: When two lines never meet, no matter how far they are extended, and they lie in the same plane.
- Circle: A set of points in a plane that are all equidistant from a fixed center point.
- Radius: The distance from the center of a circle to any point on its boundary.
By mastering these key terms, you’ll be better equipped to understand and approach problems in this area of study. Familiarity with the vocabulary enables smoother comprehension of more complex concepts as they are introduced.
How to Interpret Diagrams in Mathematical Problems
Interpreting diagrams correctly is essential when solving mathematical problems, as they visually represent relationships between different elements. Understanding the structure of a diagram helps in identifying the necessary steps to find a solution. In this section, we will explore how to read and analyze diagrams effectively to apply the right strategies for problem-solving.
Identifying Key Elements
Mathematical diagrams typically include various components like points, lines, angles, and shapes. The first step in interpreting a diagram is to identify these elements and understand their relationships. Look for:
- Points: Marked locations, often labeled with letters, indicating important positions in the diagram.
- Lines and Segments: These represent straight paths connecting points. Pay attention to whether lines are parallel, perpendicular, or intersecting.
- Angles: Angles between intersecting lines or segments are often labeled with small arcs or symbols indicating their measurement.
- Shapes: Different shapes like triangles, squares, and circles may appear. Recognizing the properties of these shapes is crucial for applying the correct formulas.
Understanding Relationships and Labels
Next, it is essential to understand the relationships between the elements shown in the diagram. Often, diagrams come with labels or additional markings that provide further information, such as:
- Angle Notations: Angles may be marked with symbols or numbers that indicate their measure, such as 90° for a right angle or x° for an unknown value.
- Equal Lengths: In some diagrams, lines or segments that are equal in length are marked with identical tick marks.
- Parallel and Perpendicular Lines: These may be indicated with special markings, such as arrows or boxes, to help identify their properties.
By carefully analyzing the diagram and understanding these visual cues, you can determine the best way to approach the problem and solve it accurately. Interpreting diagrams is a skill that becomes easier with practice, so make sure to pay close attention to each detail provided in the image.
Finding Patterns in Mathematical Problems
Recognizing patterns is a powerful tool when approaching problems in mathematics. By identifying repeating elements, structures, or relationships between figures, you can often simplify complex problems and make connections to previously solved examples. This section will guide you through how to spot and use patterns effectively to enhance your problem-solving skills.
Mathematical problems often involve recurring themes or geometric arrangements that can lead to shortcuts in finding solutions. Recognizing these repetitions or relationships allows for faster, more efficient problem-solving. Here are some ways to detect patterns:
- Look for Symmetry: Many shapes and figures exhibit symmetry. Identifying lines of symmetry, rotational symmetry, or reflective symmetry can reveal equivalent parts or simplify calculations.
- Analyze Proportions: In some problems, the ratios between different elements remain constant. Identifying proportional relationships between sides or angles can often lead to quicker solutions through the use of scaling or similar figures.
- Identify Common Properties: Common properties, such as the Pythagorean Theorem in right triangles or properties of parallel lines, often appear across different problems. Recognizing these properties can help you apply the correct formulas more easily.
- Use Previous Results: If you’ve encountered similar problems before, try to recall the methods or strategies used to solve them. This can save time and effort, as many problems in mathematics follow a set pattern.
By consistently looking for these patterns, you can develop a more intuitive understanding of the problems you face. With practice, identifying patterns becomes second nature, allowing you to solve problems more efficiently and with greater confidence.
Tips for Tackling Challenging Mathematical Questions
When faced with difficult mathematical problems, it can be easy to feel overwhelmed. However, with the right approach, even the most challenging questions can be broken down into manageable steps. This section outlines key strategies that will help you approach complex problems with confidence and efficiency.
One of the most important skills in problem-solving is the ability to approach a question methodically. Here are some effective tips to guide you through tough problems:
- Break the Problem into Smaller Parts: Large problems can often be intimidating, but they usually consist of smaller, simpler steps. Start by identifying the basic components of the problem, then tackle each one individually. Breaking down the task makes it less overwhelming and more manageable.
- Draw Diagrams and Visualize: Many challenging problems become easier when you can see them. Drawing diagrams helps you visualize the relationships between different elements and can lead to clearer insight into the solution process.
- Work Backwards: If you’re struggling to find a solution, try working backwards from the desired result. This reverse-engineering approach can often provide a fresh perspective and reveal steps you may have missed when working forwards.
- Look for Patterns and Relationships: Mathematical problems often involve repeating patterns or relationships between numbers or shapes. Identifying these connections early on can simplify the problem and guide you towards the solution.
- Use Known Formulas and Theorems: Many problems can be solved by applying familiar mathematical rules, formulas, or theorems. Make sure you are comfortable with the basic principles, and try to apply them wherever possible.
- Take Breaks When Needed: Sometimes, stepping away from a difficult problem for a short time can help clear your mind and lead to new insights. Giving yourself a break can prevent frustration and help you approach the problem with a fresh perspective.
By following these strategies, you can build your confidence in tackling difficult mathematical challenges. Remember, persistence and a methodical approach are key to success in solving complex questions.
Building a Strong Foundation in Mathematics
To succeed in any field of mathematics, it’s essential to establish a solid understanding of the foundational principles. Without a strong base, it’s easy to become confused when encountering more complex concepts. This section explores effective strategies for building a strong mathematical foundation that will support advanced learning and problem-solving skills.
The first step to mastering any mathematical discipline is understanding the basic elements. Whether you are working with shapes, numbers, or equations, grasping the foundational principles is crucial. The goal is to be comfortable with the fundamental concepts so that as topics become more challenging, you are able to build on that knowledge.
Mastering Basic Concepts
Start by ensuring a firm grasp of the elementary concepts. This includes understanding simple geometric shapes, their properties, and the relationships between them. Knowing the basics–such as angles, lines, and measurements–is essential before moving on to more complex topics.
- Understand Key Terminology: Each mathematical field has its own set of terms. Familiarize yourself with terms related to shape properties, measurements, and geometric transformations.
- Practice Basic Calculations: Becoming proficient in basic arithmetic and algebraic calculations will give you the tools needed for solving more advanced problems. The more you practice, the more efficient you’ll become at identifying the correct approaches.
- Visualize Problems: Learning to draw diagrams and create visual representations of problems can help you see patterns and make logical connections. The ability to visualize mathematical problems is a powerful skill that simplifies even the most complex tasks.
Building Confidence Through Practice
Consistency is key when developing your mathematical skills. Practicing regularly helps reinforce your understanding and builds confidence in your problem-solving abilities. By working through various problems, you can identify areas where you need improvement and focus on those weaknesses.
- Start with Simple Problems: Begin with problems that are straightforward and gradually increase the difficulty level as you improve. Starting easy allows you to build confidence before tackling tougher challenges.
- Review Mistakes: Reviewing errors is just as important as practicing correctly. Understanding why you made a mistake and how to correct it is a key part of the learning process.
By focusing on these foundational strategies, you’ll be able to approach advanced mathematical problems with a clear, confident mindset. Establishing a strong foundation ensures that you’ll be equipped with the knowledge and skills needed to succeed in more complex areas of study.
Real-World Applications of Mathematical Concepts
The principles learned in mathematics extend far beyond the classroom. They have real-world applications that are crucial in a variety of industries and everyday situations. Understanding how these abstract concepts relate to the world around us enhances both the practical value and the enjoyment of studying mathematics.
From construction to technology, mathematical concepts are at the core of many fields. Whether designing buildings, developing software, or even navigating through cities, the skills learned in mathematics help solve problems and optimize solutions in countless ways. In this section, we will explore some key areas where mathematical principles are applied in real-life scenarios.
Architecture and Design
In architecture, understanding spatial relationships and measurements is essential. Professionals use mathematical concepts to design structures that are both functional and aesthetically pleasing. For example, determining the optimal angle of a roof, the proportions of a building, and the correct placement of windows requires a deep knowledge of geometric principles.
- Building Design: Architects use geometric shapes and angles to design stable structures. Triangles are often used for support due to their inherent stability, while the use of symmetry and proportions is key to creating aesthetically balanced designs.
- Space Planning: In interior design, mathematical knowledge helps to maximize space, ensuring that rooms are functional and meet the needs of the occupants.
Technology and Engineering
In the fields of technology and engineering, mathematical models are used to solve complex problems. From designing computer algorithms to building machinery, geometry plays a crucial role in shaping the world of innovation.
- Computer Graphics: Digital artists use geometric algorithms to create realistic graphics in video games and movies. Techniques such as rendering 3D shapes, lighting, and textures all rely on geometric principles.
- Engineering Structures: Engineers apply mathematical concepts to design bridges, roads, and transportation systems. Understanding forces, materials, and geometric shapes is essential to ensuring that these structures are safe and efficient.
These are just a few examples of how mathematical principles are applied in real life. By recognizing the practical value of these concepts, students and professionals alike can appreciate the relevance of their studies and see how math impacts the world in profound ways.
Improving Problem-Solving Skills
Mastering problem-solving is a vital skill, not just in academics, but in everyday life. Whether you’re tackling complex puzzles or making quick decisions, refining your ability to approach challenges systematically can significantly enhance your effectiveness. In mathematics, this process involves understanding concepts, developing strategies, and practicing regularly to sharpen your skills. The goal is not only to arrive at the correct solution but also to improve your thinking process along the way.
There are several strategies that can help you enhance your problem-solving abilities. These methods focus on breaking down complex problems into smaller, more manageable steps, understanding underlying patterns, and applying learned techniques to find solutions more efficiently. Below are a few tips that can help you become more adept at solving mathematical problems:
- Understand the Problem Thoroughly: Take time to read the problem carefully. Identify key information and highlight what is being asked. This initial step helps to form a mental picture and better structure your solution.
- Visualize the Problem: Sketching diagrams or drawing shapes can often reveal important insights. Many problems become clearer when you visualize the relationships between elements.
- Break the Problem Down: Divide the larger problem into smaller parts. Solve each part step by step to make the overall problem easier to tackle.
- Use Logical Deduction: Apply logical reasoning to eliminate impossible solutions and narrow down the possibilities. Deductive reasoning can help you move from known facts to unknowns systematically.
- Practice Regularly: Problem-solving is a skill that improves with consistent practice. Work on a variety of problems to develop flexibility in your approach and to strengthen your understanding of key principles.
By employing these techniques, you can improve not only your mathematical abilities but also your overall problem-solving capacity. As you practice and encounter different types of challenges, you will gain confidence and enhance your analytical skills, making it easier to approach complex problems in the future.