
Successfully navigating mathematical challenges requires more than just memorizing formulas; it demands understanding key principles, developing problem-solving skills, and applying strategies that streamline the process. Whether you’re tackling derivatives or integrals, each concept builds on the previous one, requiring both theoretical knowledge and practical application.
Preparation is key to overcoming the most difficult problems. Knowing how to approach each task, identifying critical steps, and avoiding common pitfalls can drastically improve your performance. With consistent practice and a clear strategy, even the most complex questions become manageable.
Confidence plays a major role when facing these types of assessments. The more familiar you become with the methods and solutions, the more adept you will be at recognizing patterns and applying techniques correctly under pressure. Mastery is a journey that involves persistent effort, review, and refinement of your skills.
Calculus Exam Answers for Students
For students preparing for complex problem-solving tasks, it is essential to develop a systematic approach. The key to success lies in understanding the principles behind each problem and mastering the steps required to solve them efficiently. With the right strategies, even the most challenging questions can be tackled with confidence.
One of the most important skills is identifying the appropriate methods to apply based on the question type. It is vital to recognize patterns, such as when to use integration techniques or apply differentiation rules. Proper preparation helps minimize errors and boosts accuracy in solving mathematical problems under time constraints.
| Step | Description | Example |
|---|---|---|
| Step 1 | Analyze the question to identify the key variables and operations. | For a rate of change problem, identify the function’s variables. |
| Step 2 | Determine which technique to use based on the question type. | If asked to find a derivative, apply the chain rule or product rule. |
| Step 3 | Carefully perform the calculation, paying attention to signs and coefficients. | When integrating, ensure correct limits of integration are used. |
| Step 4 | Review the solution for accuracy and completeness. | Recheck computations, especially in multi-step problems. |
By following these structured steps, students can improve their approach to solving mathematical challenges. With practice, these techniques become second nature, leading to greater confidence and better performance in assessments.
Understanding Common Calculus Exam Problems

Students often encounter a variety of challenges in mathematical assessments that require different approaches to solve. These problems test not only your understanding of theoretical concepts but also your ability to apply them to specific scenarios. Recognizing the most common types of tasks can help in preparing effectively and avoiding unnecessary confusion during the test.
Function Analysis and Optimization
One of the most frequent challenges involves analyzing and optimizing functions. These problems typically ask you to find the maximum or minimum values of a given function. This requires understanding the behavior of the function, determining critical points, and applying techniques such as first derivative tests and second derivative tests to evaluate and classify these points.
Rate of Change and Related Rates

Another common category involves rate-of-change problems, where you are tasked with finding how one variable changes in relation to another. These problems often involve related rates, requiring you to use implicit differentiation and carefully apply given relationships between different quantities. A strong grasp of derivative rules and chain rule applications is essential in solving such problems accurately.
Mastering these common types of questions will not only improve your problem-solving skills but also give you a clear strategy for approaching unfamiliar problems during assessments.
How to Approach Calculus Test Questions

When facing mathematical problems on an assessment, a clear strategy can make all the difference. Knowing how to tackle each problem systematically can help reduce errors and increase efficiency. The key is to break down the question into manageable parts and apply the appropriate techniques based on the task at hand.
Start by carefully reading the question to identify what is being asked. Take note of any given information and think about the best approach to solving the problem. If the question involves a function, for example, determine whether it requires differentiation, integration, or another method. Always begin with the simplest step and build up to the more complex ones.
As you work through the problem, stay organized and keep track of intermediate steps. This ensures that if an error occurs, it’s easier to identify where things went wrong. Finally, before concluding, review the solution to ensure all aspects of the question have been addressed and the answer makes sense in the context of the problem.
Effective Strategies for Solving Calculus Problems
Approaching mathematical problems requires a structured method to ensure accuracy and efficiency. By mastering certain techniques and strategies, you can tackle a variety of problems with confidence. Success often depends on how well you understand the core concepts and how quickly you can identify the most appropriate approach for each question.
One key strategy is to start by understanding the problem’s context. Break it down into smaller parts and identify the goal–whether it’s finding a rate of change, optimizing a function, or determining an area under a curve. Once you understand what’s being asked, select the method that aligns with the task. For instance, integration or differentiation may be necessary, but knowing when to apply each technique is crucial for accuracy.
Another effective approach is to simplify complex problems. When possible, reduce the problem to simpler components that are easier to manage. This can involve factoring functions, breaking down complex expressions, or using substitution methods. Additionally, always check intermediate results to ensure you’re on the right track before moving on to the next step.
Top Mistakes to Avoid During Exams
During assessments, even small errors can lead to significant consequences. Recognizing common pitfalls and understanding how to avoid them can drastically improve your performance. Focusing on accuracy and following a systematic approach can help prevent mistakes that often arise under time pressure.
1. Misinterpreting the Question
One of the most frequent mistakes is misinterpreting what is being asked. This often leads to using the wrong method or missing key details. To avoid this:
- Carefully read the question multiple times before starting.
- Highlight or underline important information to ensure you don’t overlook any details.
- Identify the type of problem (e.g., optimization, rate of change, area under the curve) to guide your solution.
2. Rushing Through Calculations
Speed is important, but rushing can result in simple computational errors. To avoid this:
- Write down each step clearly to avoid skipping important processes.
- Check your calculations as you go along to catch errors early.
- Allow yourself time to review your work before submitting it.
3. Overlooking Sign Errors
Sign errors, such as forgetting a negative sign or misplacing a subtraction, can lead to incorrect answers. This is especially common in problems involving derivatives or integrals. To minimize these mistakes:
- Pay extra attention to the signs when differentiating or integrating.
- Double-check the signs in your final result before concluding.
4. Failing to Review Your Work
Many mistakes occur simply because students don’t review their work before submitting it. A quick review can catch simple errors that were missed during the initial solution process. Make sure to:
- Go over your calculations and check that all steps are logical and consistent.
- Verify that the final solution answers the original question.
Key Concepts to Master for Success
To excel in mathematical assessments, it is crucial to have a strong grasp of fundamental principles that form the foundation of problem-solving. Mastery of these core concepts not only boosts your ability to approach questions with confidence but also enhances your capacity to think critically and apply the right techniques in various scenarios.
One key area is understanding the behavior of functions and how to manipulate them effectively. This includes knowledge of limits, continuity, and the ability to identify critical points, which are essential when solving optimization and rate-of-change problems. A deep understanding of these concepts will allow you to identify patterns and apply the appropriate methods more efficiently.
Another vital concept is mastering differentiation and integration techniques. These tools are fundamental for solving a wide range of problems, from finding slopes to calculating areas under curves. A strong command of rules such as the chain rule, product rule, and integration by parts is necessary for handling complex tasks effectively.
Finally, understanding how to apply these concepts in real-world contexts is equally important. This includes recognizing when and how to use mathematical models, interpreting the results, and ensuring the solutions are relevant to the problem at hand. By mastering these key ideas, you can approach each challenge with clarity and precision, ultimately leading to better results.
How to Organize Your Exam Time
Effective time management is essential for performing well under pressure. When facing a series of mathematical problems, organizing your time ensures that you can allocate sufficient attention to each question while avoiding unnecessary stress. The key is to balance speed with accuracy, ensuring that every aspect of the task is addressed without rushing.
1. Review the Entire Test First
Before diving into any problem, take a few minutes to scan through the entire assessment. Identify the types of questions and note how much time you can realistically spend on each one. This strategy helps you prioritize more challenging tasks and gives you an overview of the content, allowing you to approach the test more confidently.
2. Allocate Time Wisely
Once you’ve assessed the test, divide your time based on the number of questions and their complexity. For questions that require more in-depth problem-solving, allocate extra time, but don’t spend too much time on one question. A general guideline is to give easier problems around 10–15 minutes and leave the more challenging ones 20–25 minutes, allowing you time to review your answers at the end.
Tip: If you’re stuck on a question, move on and come back to it later. This ensures you don’t waste valuable time on one problem at the expense of others.
By managing your time carefully and following a structured approach, you can ensure that you complete the assessment effectively and with less stress.
Using Graphs and Diagrams in Tests
Visual representations are powerful tools for understanding complex mathematical problems. Graphs and diagrams can provide clarity and help you visualize key relationships between variables. Utilizing these tools effectively can simplify the problem-solving process and make it easier to identify important features of the problem.
Here are some strategies for using graphs and diagrams in assessments:
- Sketching Functions: Drawing a quick sketch of a function can help you understand its behavior. Look for intercepts, asymptotes, and turning points to gain insight into how the function behaves.
- Visualizing Derivatives: Graphs can help you visualize the slope of a function and the behavior of its derivatives. This is especially useful when solving optimization problems or finding local extrema.
- Using Area Representations: Diagrams can help when calculating areas under curves or between functions. Labeling the region clearly can assist in understanding integral problems.
- Highlighting Key Information: Use diagrams to mark important points or features, such as critical points, inflection points, or regions of interest. This will help you stay focused on the critical aspects of the problem.
Incorporating graphs and diagrams not only aids in better comprehension but can also help you avoid mistakes that arise from purely algebraic manipulation. Make sure to take the time to draw clear, accurate representations, as they can significantly enhance your problem-solving process.
Helpful Tips for Integration Problems
When dealing with problems that require finding the accumulation of quantities or areas under curves, having a systematic approach can make all the difference. Integration, while powerful, can sometimes be tricky, especially when faced with complex expressions. The key to solving these problems efficiently is to apply a set of useful techniques and strategies.
Here are some helpful tips to keep in mind when tackling integration problems:
- Check for Simpler Forms: Always see if you can simplify the expression before proceeding with integration. Look for common factors or algebraic manipulations that can make the problem easier.
- Recognize Standard Integrals: Familiarize yourself with common integration formulas, such as those for polynomials, trigonometric functions, and exponentials. Recognizing these can save you time and effort.
- Use Substitution When Necessary: If the integral contains a composite function, consider using substitution. This technique can transform the problem into a simpler form that’s easier to integrate.
- Don’t Forget Constants: After integrating, remember to add the constant of integration (C) if the problem calls for an indefinite integral. Forgetting this step is a common oversight.
By following these tips and practicing regularly, you can improve your ability to handle integration problems and enhance your problem-solving efficiency.
Derivatives: Key Rules and Applications
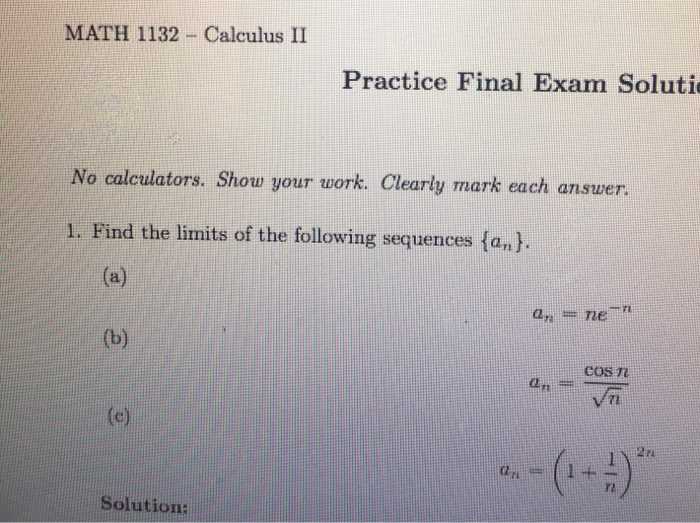
Understanding how quantities change with respect to each other is central to solving many mathematical problems. Derivatives provide a powerful tool for analyzing rates of change and understanding the behavior of functions. Mastering key rules and learning how to apply them can significantly simplify the process of finding derivatives and solving related problems.
Here are some important rules and their applications:
- Power Rule: For any function of the form (f(x) = x^n), the derivative is given by (f'(x) = n cdot x^{n-1}). This is one of the most frequently used rules, applicable to polynomials and functions involving exponents.
- Product Rule: When differentiating a product of two functions, (f(x) = g(x) cdot h(x)), use the formula: (f'(x) = g'(x) cdot h(x) + g(x) cdot h'(x)). This is useful when dealing with products of more complex functions.
- Quotient Rule: For the division of two functions, (f(x) = frac{g(x)}{h(x)}), the derivative is given by (f'(x) = frac{g'(x) cdot h(x) – g(x) cdot h'(x)}{h(x)^2}). This helps when differentiating rational functions.
- Chain Rule: Used for compositions of functions, the chain rule states that for (f(x) = g(h(x))), the derivative is (f'(x) = g'(h(x)) cdot h'(x)). This is critical for differentiating nested functions.
Applications of derivatives are numerous and diverse. Some common areas include:
- Optimization: Derivatives are often used to find maximum and minimum values of functions, which is important in areas such as economics, physics, and engineering.
- Motion and Rates: Derivatives are key to understanding velocity and acceleration in motion problems, as they describe the rate of change of position with respect to time.
- Curve Sketching: Derivatives help in determining the behavior of a graph, such as identifying turning points, concavity, and inflection points.
By mastering these rules and their applications, you can confidently approach and solve a wide range of problems involving rates of change and function behavior.
Advanced Techniques for Success

In many higher-level assessments, complex problems require a deeper understanding of advanced techniques. Mastering these methods can significantly improve your ability to tackle intricate questions, providing you with the tools to solve problems more efficiently and accurately. These techniques build on foundational principles but involve more sophisticated strategies for handling challenging problems.
Key Methods to Master
Here are some advanced approaches that can enhance your performance:
- Partial Fractions Decomposition: This technique is especially useful when dealing with rational functions. It involves breaking down a complex fraction into simpler components, making it easier to integrate or differentiate.
- Multiple Integrals: In problems involving areas or volumes in multiple dimensions, double and triple integrals allow you to calculate complex regions. Understanding how to set up and evaluate these integrals is crucial for higher-level problems.
- Integration by Parts: A method based on the product rule for differentiation, this technique is particularly useful when integrating the product of two functions. It is essential for solving integrals that do not have simple antiderivatives.
- Series Expansions: Expanding functions into series, such as Taylor or Maclaurin series, can be a powerful tool for approximating solutions when exact methods are difficult or impossible to apply.
Applying Techniques Under Time Pressure
During assessments, applying advanced methods effectively requires both understanding and practice. It’s important to manage your time well, ensuring you apply the most efficient strategy for each problem. Additionally, always verify your answers by checking for consistency or using alternative methods when time allows.
By mastering these advanced techniques, you’ll be able to approach problems with more confidence, allowing you to navigate even the most challenging questions with greater ease and accuracy.
Commonly Tested Formulas
In advanced mathematics, certain formulas are essential for solving a wide range of problems efficiently. These formulas form the foundation of many key concepts, making them crucial for successful problem-solving. Whether working with rates of change, areas under curves, or other related concepts, knowing these formulas can significantly speed up your calculations and improve accuracy.
Essential Differentiation Formulas
The following formulas are commonly used to differentiate functions:
- Power Rule: For ( f(x) = x^n ), the derivative is ( f'(x) = n cdot x^{n-1} ).
- Product Rule: If ( f(x) = g(x) cdot h(x) ), then ( f'(x) = g'(x) cdot h(x) + g(x) cdot h'(x) ).
- Quotient Rule: For ( f(x) = frac{g(x)}{h(x)} ), the derivative is ( f'(x) = frac{g'(x) cdot h(x) – g(x) cdot h'(x)}{h(x)^2} ).
- Chain Rule: For ( f(x) = g(h(x)) ), the derivative is ( f'(x) = g'(h(x)) cdot h'(x) ).
Key Integration Formulas
When it comes to integration, the following formulas are frequently encountered:
- Power Rule for Integration: For ( int x^n dx ), the integral is ( frac{x^{n+1}}{n+1} + C ) (for ( n neq -1 )).
- Integration by Parts: For ( int u dv = uv – int v du ), this is useful when the integrand is a product of two functions.
- Substitution: If ( u = g(x) ), then ( int f(g(x)) g'(x) dx = int f(u) du ). This simplifies integrals involving composite functions.
- Trigonometric Integrals: Standard formulas such as ( int sin(x) dx = -cos(x) + C ) and ( int cos(x) dx = sin(x) + C ) are essential for solving trigonometric integrals.
By familiarizing yourself with these formulas and practicing their application, you can improve your problem-solving efficiency and tackle complex problems with ease.
How to Check Your Solutions

When solving mathematical problems, verifying your results is essential to ensure accuracy. Checking your work helps identify potential errors in reasoning or calculation. By applying various techniques, you can confirm whether your results are correct or if further revisions are needed.
Strategies for Verification
Here are some effective methods for double-checking your solutions:
- Recalculate Using Different Approaches: If possible, try solving the problem using an alternative method or formula. If both methods lead to the same result, it’s likely correct.
- Check Units and Dimensions: For problems involving real-world quantities, verify that your final units or dimensions match the expected outcomes. Consistency in units can help detect mistakes.
- Estimate and Compare: Before diving into detailed calculations, make a rough estimate of the answer based on the problem’s context. If your final result is significantly different from this estimate, recheck your steps.
Utilizing Technology for Validation
Many online tools and software can help validate solutions. Graphing calculators or mathematical software can quickly plot functions or check integral and derivative values, providing instant feedback. However, always ensure that your understanding of the solution process is sound, even when using technology.
By carefully reviewing each step and applying these verification techniques, you can enhance the accuracy of your solutions and improve overall confidence in your work.
Overcoming Test Anxiety
Many students experience anxiety before and during assessments, especially when faced with complex mathematical problems. The pressure to perform well can lead to stress, which may negatively affect focus and performance. However, with the right strategies, it is possible to manage this anxiety and approach tests with a calm and focused mindset.
Techniques for Reducing Anxiety

Here are some effective strategies to help manage nervousness and boost confidence:
- Preparation is Key: Consistent practice is the most effective way to build confidence. Familiarity with common problem types and solutions can reduce uncertainty and anxiety when facing similar questions.
- Mindfulness and Breathing Exercises: Deep breathing or mindfulness techniques can help reduce immediate stress and clear your mind. Taking a few moments to focus on your breath can calm nerves and improve concentration during the test.
- Positive Self-Talk: Encourage yourself with affirmations and a positive mindset. Reassure yourself that you have prepared well and that you are capable of solving the problems in front of you.
- Visualize Success: Before the test, take a moment to visualize yourself approaching the problems confidently and solving them effectively. Positive visualization can set the stage for success.
Creating a Test-Day Routine
Establishing a routine before the test can also help minimize anxiety. Ensure that you get enough rest the night before and eat a nutritious meal. Arriving at the test location early can help you settle in and mentally prepare. Having a clear, focused mindset will allow you to approach each problem methodically, without the distraction of stress.
By adopting these strategies, you can reduce anxiety and improve your ability to perform under pressure, making the test-taking experience more manageable and less overwhelming.
Review: What to Focus On
When preparing for an important assessment in mathematics, it is crucial to focus on the key concepts and problem types that are most likely to appear. Rather than attempting to cover every single topic, directing your attention to the areas that are frequently tested will maximize your chances of success. Understanding the core principles behind each type of problem will allow you to approach the test with confidence and efficiency.
Core Topics to Master
Some topics are essential to your overall understanding and are commonly featured in tests. Make sure to review these concepts thoroughly:
- Function Behavior: Knowing how different functions behave–whether increasing or decreasing, concave up or concave down–forms the foundation for solving many problems.
- Limits and Continuity: Understanding the concept of limits is vital for solving problems involving approximation, rates of change, and asymptotes.
- Derivatives and Applications: Focus on mastering the rules of differentiation and how they apply to real-world problems such as motion, optimization, and rates of change.
- Integration Techniques: Practice various integration methods, from basic antiderivatives to more complex techniques like integration by parts and substitution.
Problem Solving Skills
In addition to mastering theory, being able to solve problems efficiently is just as important. During your review sessions, practice solving problems under timed conditions to improve your speed and accuracy. Familiarize yourself with different problem types such as word problems, graphical analysis, and abstract equations to ensure you’re prepared for any challenge the test may present.
By honing in on these key areas, you’ll be able to approach the test with a clear focus, knowing exactly where to apply your skills and knowledge for the best results.
Importance of Practice for Success
When preparing for any academic assessment, one of the most effective strategies is consistent and focused practice. The more problems you solve, the more confident and proficient you become in applying concepts and techniques. This process helps not only in reinforcing your understanding but also in familiarizing you with various problem types that may appear during the test.
Through repeated practice, you develop a deeper intuition for problem-solving. This allows you to quickly identify patterns and apply the most appropriate methods. Furthermore, practicing under timed conditions mimics the pressure of an actual test and helps you improve your speed and accuracy.
Why Practice Makes Perfect
Consistency: Regular practice ensures that the concepts you learn stay fresh in your mind. It also helps you recognize and address weak areas before the actual assessment.
Confidence: Solving a wide range of problems boosts your confidence, allowing you to approach any challenge with a clearer mindset.
Improved Problem-Solving Skills: The more problems you encounter, the more strategies you can develop, leading to faster and more effective solutions.
By dedicating time to practice, you ensure that you are fully prepared for any challenge, giving you the best chance for success when the time comes.
How to Stay Focused During Your Test
Maintaining concentration during a high-stakes academic assessment is key to performing at your best. Distractions, both internal and external, can easily derail your progress, but with the right strategies, you can stay focused and calm throughout the entire process. Developing good habits and learning to manage your attention will help you stay on track and efficiently complete each task.
One of the most effective ways to stay focused is to break the test into smaller, more manageable sections. Instead of feeling overwhelmed by the entire assessment, focus on one question at a time. By setting clear, short-term goals, you can maintain a steady pace and keep your mind from wandering.
Techniques for Staying Focused
Prioritize and Organize: Start with questions that you find easier to boost your confidence. Then, tackle the more difficult ones when your focus is sharp.
Mindful Breathing: If you feel your attention slipping, take a few deep breaths to reset your mind. This simple technique can help refocus your thoughts and reduce anxiety.
Avoiding Common Pitfalls
Don’t Overthink: Second-guessing yourself can lead to wasted time and unnecessary stress. Trust your first instinct and move on if you’re unsure.
Stay Calm: Keep your stress levels in check by staying positive. A calm mind is more effective in problem-solving than one filled with anxiety.
By using these methods, you can improve your focus and stay on task, allowing you to perform at your peak when it matters most.