
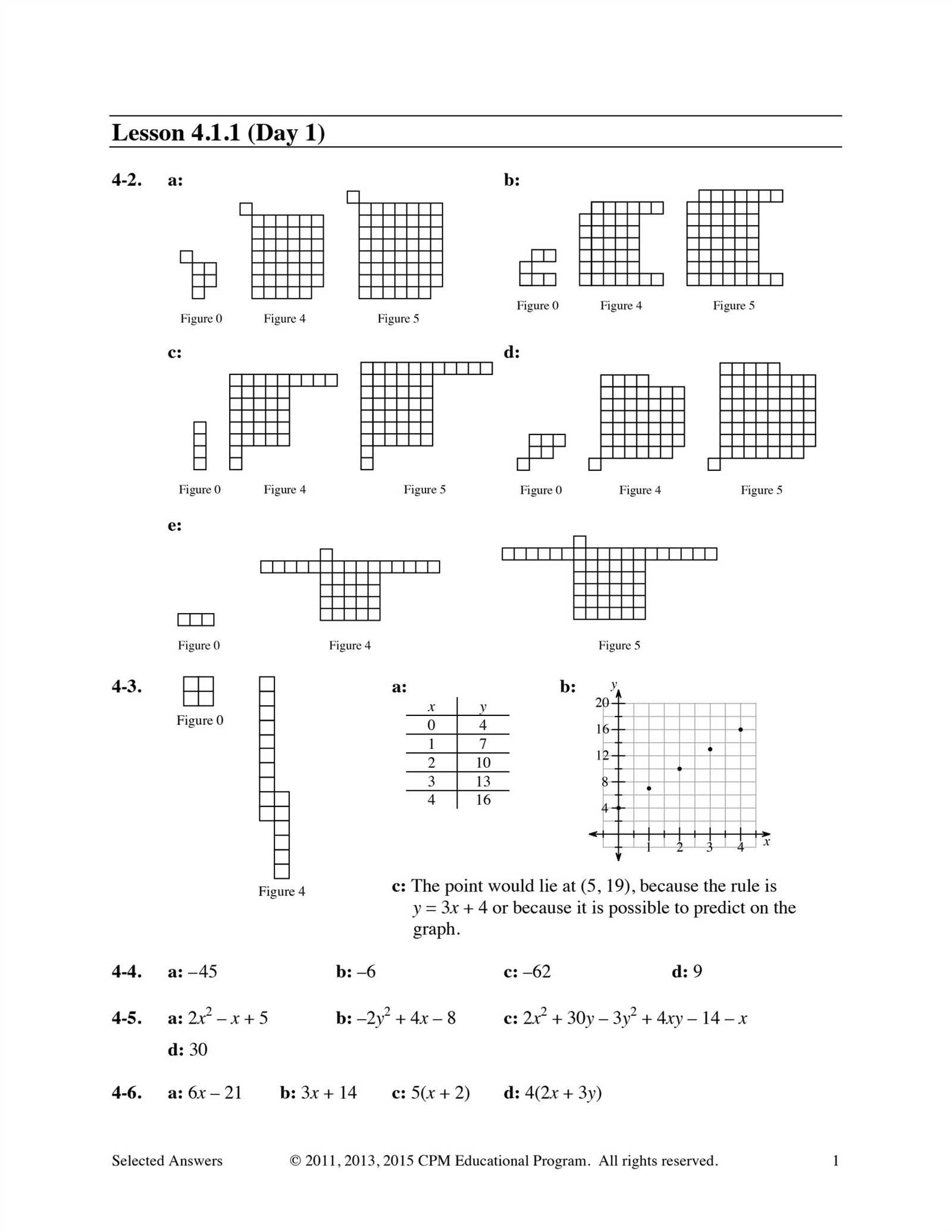
In this section, students explore essential mathematical principles that lay the foundation for solving complex equations and real-world scenarios. With a focus on logical reasoning and critical thinking, the exercises guide learners through a variety of problem types, helping to strengthen their understanding of key concepts.
By working through these problems, students can improve their ability to recognize patterns, manipulate variables, and apply strategies to solve different types of equations. As they progress, they develop a deeper insight into how mathematical relationships work and how to use them in problem-solving.
Whether you’re tackling basic calculations or more advanced topics, the focus is on building the skills necessary for success in future math challenges. With each problem set, the aim is to enhance confidence and precision in solving complex tasks.
CPM Algebra 1 Chapter 4 Answers Overview
This section offers a comprehensive look at essential problem-solving techniques and methods to approach a variety of mathematical tasks. By carefully analyzing each problem, learners gain a deeper understanding of how mathematical principles apply in different scenarios. The goal is to help students strengthen their skills and confidence when facing more complex equations in future lessons.
Key Concepts Covered
- Understanding and solving linear relationships
- Manipulating expressions with variables
- Recognizing patterns and applying strategies
- Mastering calculations for equations and inequalities
- Utilizing step-by-step procedures to ensure accuracy
How This Section Helps Students
Through focused practice and detailed solutions, this section ensures that learners are not only able to solve problems correctly but also understand the underlying methods that make the process efficient. By working through various examples, students can approach challenges with clarity and precision.
Key Concepts in Chapter 4
This section focuses on important mathematical principles that are essential for solving a wide range of problems. By working through various examples, students can grasp the underlying techniques that make complex equations more manageable. The goal is to build a strong foundation that supports more advanced problem-solving strategies in future lessons.
Understanding Relationships and Variables
One of the key aspects covered is recognizing relationships between different variables and how they influence each other. Students learn how to manipulate these relationships and solve for unknowns in different contexts. By understanding how variables interact, learners can approach problems with a clearer perspective and develop stronger reasoning skills.
Techniques for Solving Equations
The section also introduces various techniques for solving both simple and complex equations. These methods are designed to help students solve problems step by step, ensuring that no critical detail is overlooked. By following these strategies, learners can systematically break down and solve any equation with greater accuracy.
Step-by-Step Solutions for Problems
In this section, the focus is on breaking down complex problems into manageable steps, allowing students to systematically approach each task. By following a clear sequence, learners can identify key operations and solve challenges with confidence. This methodical approach helps to reduce errors and builds a solid understanding of the problem-solving process.
Breaking Down the Problem
The first step is to carefully analyze the given information and identify what is being asked. Once the problem is fully understood, the next stage involves selecting the appropriate strategy or method to solve it. Each decision is based on previous knowledge and logical reasoning.
Executing the Solution

After determining the right approach, the next step is to perform the necessary calculations or manipulations. By following the steps one at a time, students can work through the problem without missing critical details. Each solution is carefully constructed to ensure accuracy, leading to the final result with confidence.
Understanding Algebraic Expressions in Chapter 4
This section focuses on the fundamentals of working with mathematical phrases involving variables and constants. Students learn to identify different components of an expression, including terms, coefficients, and exponents. Mastering these concepts allows for a deeper understanding of how to manipulate and simplify various mathematical structures.
Identifying Terms and Coefficients
Each expression is composed of individual parts, known as terms. In this section, learners focus on how to break down each term and identify its components, such as the variable and its corresponding coefficient. Understanding this helps in simplifying and solving problems efficiently.
Simplifying and Combining Like Terms
Another crucial skill covered is simplifying expressions by combining like terms. This technique ensures that expressions are written in their most concise form, making them easier to solve and interpret. Through practice, students become adept at recognizing like terms and applying the correct methods to simplify equations.
Common Mistakes in Algebra 1 Exercises
When working through mathematical problems, students often encounter certain challenges that can lead to mistakes. These errors may arise from misinterpreting instructions, skipping steps, or overlooking important details. Identifying and understanding these common mistakes is crucial for improving problem-solving skills and achieving greater accuracy.
One frequent error occurs when students fail to properly distribute or apply operations to all terms in an expression. Another common issue is neglecting to check the work after solving, which can lead to overlooked mistakes. By recognizing these patterns, learners can take steps to avoid them and refine their approach to problem-solving.
How to Approach Word Problems
Word problems can often seem intimidating, but with the right approach, they become manageable and solvable. The key is to break the problem down into smaller, more digestible parts. By carefully reading the problem and identifying key information, students can translate the words into mathematical expressions and find solutions step by step.
Steps to Solve Word Problems
- Read the problem carefully: Pay close attention to all details provided in the question.
- Identify known and unknown variables: Determine what information is given and what needs to be found.
- Choose the right mathematical operations: Based on the problem’s requirements, select the appropriate method (e.g., addition, multiplication, etc.).
- Write an equation: Translate the word problem into a mathematical equation that represents the situation.
- Solve the equation: Perform the necessary steps to find the unknown value.
- Check your answer: Ensure that the solution makes sense in the context of the problem.
By following these steps, students can build confidence and tackle word problems more effectively. The more practice they get, the more intuitive the process will become.
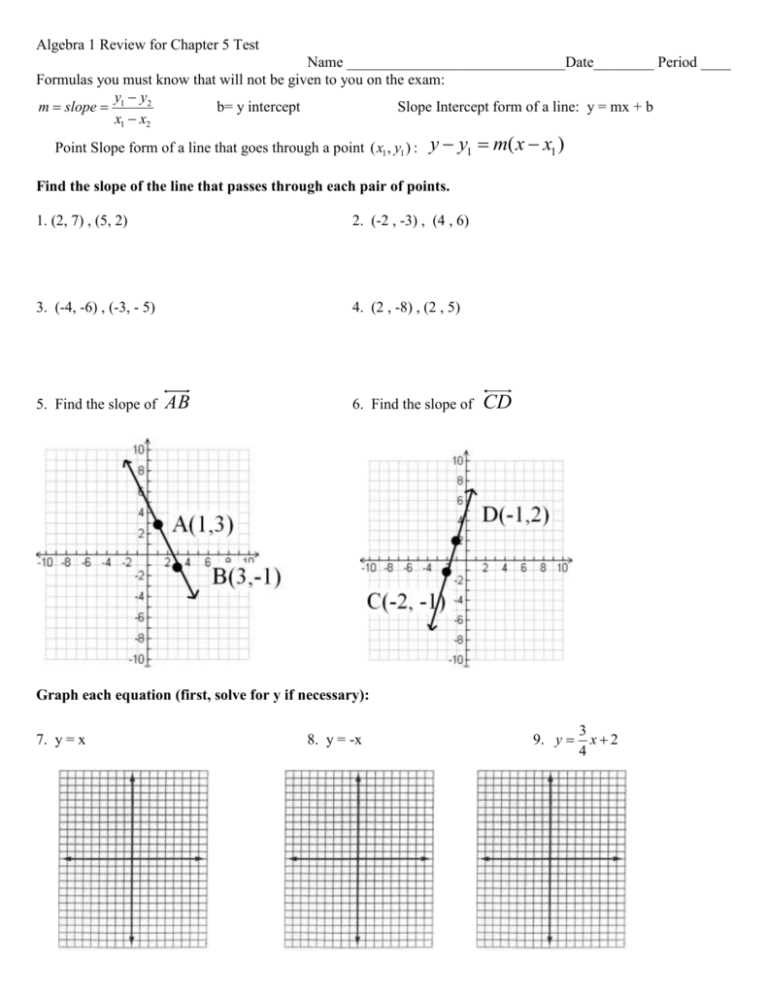
Review of Equations and Inequalities
Understanding equations and inequalities is essential for solving a wide variety of mathematical problems. Both represent relationships between variables, but they do so in different ways. Equations show equal relationships, while inequalities express a range of possible solutions. Mastering both concepts is critical for moving forward in more advanced problem-solving tasks.
Key Concepts of Equations
- Equations represent equal relationships: An equation states that two expressions are equal, and the goal is to find the value of the unknown variable.
- Solving equations: The process involves isolating the variable to determine its value.
- Types of equations: These can include linear equations, quadratic equations, and more complex forms depending on the context.
Understanding Inequalities

- Inequalities show relationships of greater or less than: An inequality expresses that one side is either greater than or less than the other, allowing for a range of possible solutions.
- Solving inequalities: This involves similar steps to solving equations, but special attention is given to reversing the inequality symbol when multiplying or dividing by negative numbers.
- Graphing inequalities: Inequalities are often represented on a number line or coordinate plane, showing all possible values that satisfy the condition.
With practice, students can become more comfortable solving both equations and inequalities, applying these techniques to a variety of scenarios with greater confidence.
Tips for Mastering Chapter 4 Topics
Mastering the concepts in this section requires focus, practice, and a solid understanding of key techniques. By applying strategic methods and breaking down complex problems into smaller steps, students can improve their skills and gain confidence in solving a variety of mathematical tasks. Here are some effective tips to help you succeed with the material covered in this section.
Focus on Understanding the Concepts
It’s important to first understand the core principles behind each problem. Don’t rush through exercises; take the time to break down the steps and understand the logic behind each solution. Understanding the reasoning makes it easier to apply the methods to different types of problems.
Practice Regularly and Consistently
Consistent practice is essential for mastery. Work through a variety of problems to strengthen your skills and ensure that you’re comfortable with all the techniques. Regular practice helps you recognize patterns and apply strategies efficiently when solving new challenges.
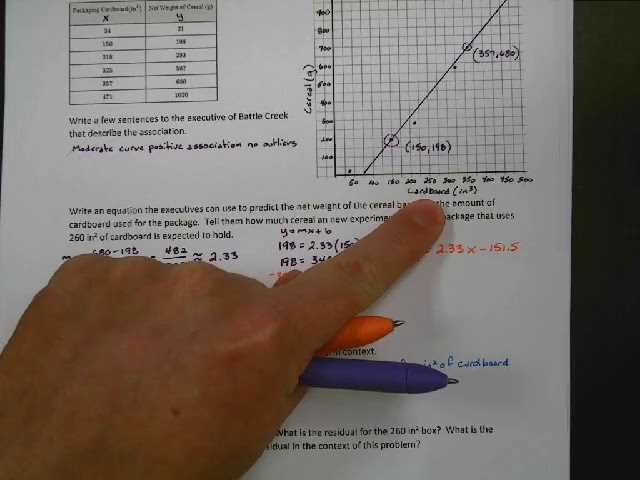
Understanding Linear Relationships and Graphing
In this section, students explore how to represent relationships between variables using graphs and equations. A linear relationship is one where changes in one variable result in a constant change in another. Understanding these relationships is crucial for solving problems that involve rate of change and proportionality. By graphing these relationships, students can visually interpret the connection between variables, making complex concepts easier to understand.
Key Features of Linear Relationships
Linear relationships are defined by their constant rate of change, which can be identified from both an equation and a graph. These relationships can be represented by straight lines, where each point on the line corresponds to a solution of the equation. The slope of the line indicates how much one variable changes in relation to the other, while the y-intercept represents the starting value of the dependent variable.
Graphing Linear Equations
Graphing a linear equation involves plotting points that satisfy the equation and connecting them to form a straight line. Here’s a simple example of how to graph a linear equation:
| x | y |
|---|---|
| 0 | 3 |
| 1 | 5 |
| 2 | 7 |
In this example, the equation is y = 2x + 3, where the slope is 2, and the y-intercept is 3. By plotting these points (0, 3), (1, 5), and (2, 7), you can draw a straight line that represents the relationship between x and y.
Strategies for Solving Quadratic Equations
Quadratic equations are a fundamental part of many mathematical problems and can be solved in several ways. Understanding the different methods available to solve these equations allows students to choose the most efficient approach based on the form of the equation. Whether factoring, completing the square, or using the quadratic formula, mastering these techniques is key to solving complex problems with confidence.
Factoring Method
Factoring is one of the most common methods for solving quadratic equations. It involves rewriting the quadratic equation as a product of two binomials, which can then be set equal to zero. Once factored, the solutions can be found by setting each factor equal to zero and solving for the variable.
Using the Quadratic Formula
When factoring is difficult or not possible, the quadratic formula provides a reliable method for solving any quadratic equation. The formula is as follows:
x = (-b ± √(b² – 4ac)) / 2a
This formula uses the coefficients from the standard form of the quadratic equation, ax² + bx + c = 0, to find the values of x. It is particularly useful when the equation does not factor easily or when the roots are irrational.
How to Check Your Answers Effectively
After solving mathematical problems, it’s crucial to verify your solutions to ensure their accuracy. Checking your work not only helps catch errors but also reinforces the methods and concepts you’ve applied. There are several techniques you can use to review your answers and ensure they are correct, making the problem-solving process more reliable and efficient.
One effective method is to substitute your solution back into the original equation. If both sides are equal, you know your solution is correct. Additionally, breaking the problem down into smaller steps and reviewing each one helps identify where mistakes may have occurred, allowing you to correct them promptly.
Using alternative methods to solve the same problem can also act as a double-check. If both methods yield the same result, you can be more confident that your answer is accurate. Finally, consider using estimation to verify the reasonableness of your solution. If your answer seems inconsistent with the context of the problem, it may be time to reassess your approach.
Using the CPM Method for Problem Solving
The CPM approach to problem solving emphasizes a structured and methodical way of tackling mathematical challenges. This method encourages students to understand concepts deeply, analyze problems step-by-step, and apply strategies that lead to effective solutions. By focusing on reasoning and critical thinking, this approach helps to build a strong foundation for problem-solving in various mathematical contexts.
Breaking Down the Problem
One of the key principles in the CPM approach is to break down the problem into smaller, more manageable parts. This involves identifying knowns and unknowns, organizing the information, and thinking about how different aspects of the problem relate to each other. By focusing on smaller pieces of the problem, students can avoid feeling overwhelmed and are more likely to find the solution more efficiently.
Using Collaborative Learning

Another critical component of the CPM method is collaboration. Working with peers provides an opportunity to share ideas, discuss different approaches, and gain new insights into problem-solving strategies. Collaborative learning allows students to tackle complex problems together and strengthens their understanding through shared knowledge and collective reasoning.
Resources for Extra Practice in Algebra 1
To strengthen mathematical skills, consistent practice is essential. Having access to additional resources can provide a variety of problems and exercises, helping reinforce concepts and improve problem-solving abilities. These tools range from interactive online platforms to printable worksheets, each designed to offer targeted practice in specific areas of mathematics.
Online Platforms are an excellent way to access a wide range of exercises tailored to different learning levels. Websites often provide step-by-step solutions, allowing students to review their work and understand the reasoning behind each step. Many platforms also offer personalized feedback, which helps identify areas for improvement.
Printable Worksheets offer another great option for extra practice. These resources can be downloaded and completed offline, allowing students to focus on specific topics without the distraction of other digital content. Many worksheets also come with answer keys, making it easier to check work and identify mistakes quickly.
Time Management Tips for Algebra 1 Students
Effective time management is crucial for students working through mathematical courses, as it allows them to balance practice, study, and assignments efficiently. With the right strategies in place, students can make the most of their study time and avoid last-minute stress. Developing a clear schedule and staying organized can help ensure consistent progress and prevent falling behind.
Establish a Study Routine
Creating a regular study schedule is one of the most effective ways to stay on track. Setting aside specific times each day for practice and review helps establish a productive routine. This consistency allows students to manage their workload and makes it easier to allocate time for more challenging topics. A well-organized study routine can also reduce procrastination and increase focus.
Prioritize Tasks
Identifying the most pressing tasks and prioritizing them is essential. Start by tackling difficult or unfamiliar topics first, when energy and concentration are highest. Once the challenging material is addressed, the remaining tasks, such as review or practice problems, can be completed with less mental effort. Keep a to-do list or planner to stay organized and ensure that important deadlines are met.
Additional Tips for Effective Time Use
- Break Study Sessions into Intervals: Use techniques like the Pomodoro Method to break study sessions into 25-minute intervals with short breaks in between.
- Minimize Distractions: Find a quiet space for studying and turn off unnecessary notifications to stay focused.
- Review Regularly: Consistent review, even for just 10-15 minutes a day, will reinforce learning and prevent cramming before exams.
Helpful Tools for Algebra 1 Learning
Mastering mathematical concepts can be challenging, but the right tools can make a significant difference in a student’s success. Whether you’re looking for resources to aid understanding, practice, or visual learning, a variety of tools can help reinforce the material. These resources are designed to make the learning process more interactive, engaging, and effective, giving students the support they need to thrive in their studies.
Among the most beneficial tools are interactive online platforms, practice apps, and graphing utilities that provide hands-on experience with solving equations and understanding mathematical relationships. Additionally, visual aids such as diagrams and step-by-step tutorials can simplify complex problems and break them down into manageable steps.
Online Platforms for Practice
Websites that offer practice problems and video tutorials are invaluable for reinforcing learning. These platforms allow students to practice problems at their own pace, track their progress, and receive instant feedback. Popular examples include:
- Khan Academy: Offers interactive lessons and practice exercises for various topics, including problem-solving and equation solving.
- Desmos: A free online graphing calculator that helps visualize mathematical relationships and solve equations graphically.
- Wolfram Alpha: A computational engine that can solve equations and provide detailed step-by-step explanations.
Graphing Calculators and Apps
Graphing calculators are essential tools for visualizing equations and understanding their behavior. Many modern apps simulate graphing calculators and offer additional features to help students solve problems. These tools allow for plotting functions, determining intercepts, and analyzing trends in the data, which enhances the learning experience.
How Chapter 4 Builds Algebraic Skills

In this section, students strengthen their mathematical abilities by exploring various problem-solving techniques and improving their understanding of mathematical relationships. The focus is on developing a deeper comprehension of the tools needed to solve more complex problems. This foundation is crucial for building proficiency in future mathematical studies.
The lessons in this part of the curriculum emphasize practical application and reinforce key skills that students will use repeatedly. As learners progress, they begin to see patterns and connections between different concepts, which helps them approach problems with greater confidence and efficiency. Each concept serves as a building block, preparing students for the challenges that follow in their academic journey.
Key Skills Developed
Throughout this section, several core skills are emphasized to enhance students’ problem-solving abilities. These include:
- Equation Solving: Understanding how to manipulate and solve equations systematically.
- Graph Interpretation: Analyzing graphical representations of mathematical relationships.
- Conceptual Understanding: Grasping the underlying principles that govern mathematical operations and their real-world applications.
Key Concepts in the Lessons
Each lesson builds upon prior knowledge, ensuring a smooth progression in skill development. The table below summarizes the primary concepts introduced:
| Lesson | Concepts Covered |
|---|---|
| Lesson 1 | Linear equations and basic graphing techniques |
| Lesson 2 | Solving inequalities and understanding their properties |
| Lesson 3 | Working with systems of equations and methods for solving them |
| Lesson 4 | Applying properties of exponents and simplifying expressions |
By the end of this section, students will have a solid understanding of these essential concepts, setting the stage for more advanced mathematical topics in the future.