
Mathematics can be challenging, but with the right approach, you can navigate through complex problems with confidence. Understanding the core principles is essential for tackling a wide range of problems. Whether you are preparing for a crucial assessment or simply looking to improve your skills, knowing the best strategies is key to achieving success.
In this section, we’ll explore various methods that can help you grasp important mathematical topics, from equations to functions. By breaking down complex ideas into simpler steps, you’ll be able to apply your knowledge more effectively. The goal is to equip you with the tools and techniques to solve problems efficiently, boosting both your understanding and performance.
Mastering Key Mathematical Problems

Achieving success in mathematical assessments requires not only understanding the key concepts but also the ability to apply them effectively. For many students, knowing the proper techniques to approach problems and identify patterns can make a significant difference in performance. This section highlights essential strategies to solve common problem types and offers guidance on how to refine your skills.
Strategies for Efficient Problem Solving
To tackle challenging questions, it’s crucial to have a structured approach. Here are some steps to consider when working through complex problems:
- Understand the problem: Carefully read each question and identify what is being asked.
- Break it down: Simplify complex expressions into manageable parts to make them easier to solve.
- Apply relevant formulas: Ensure you know the necessary formulas and how to use them correctly.
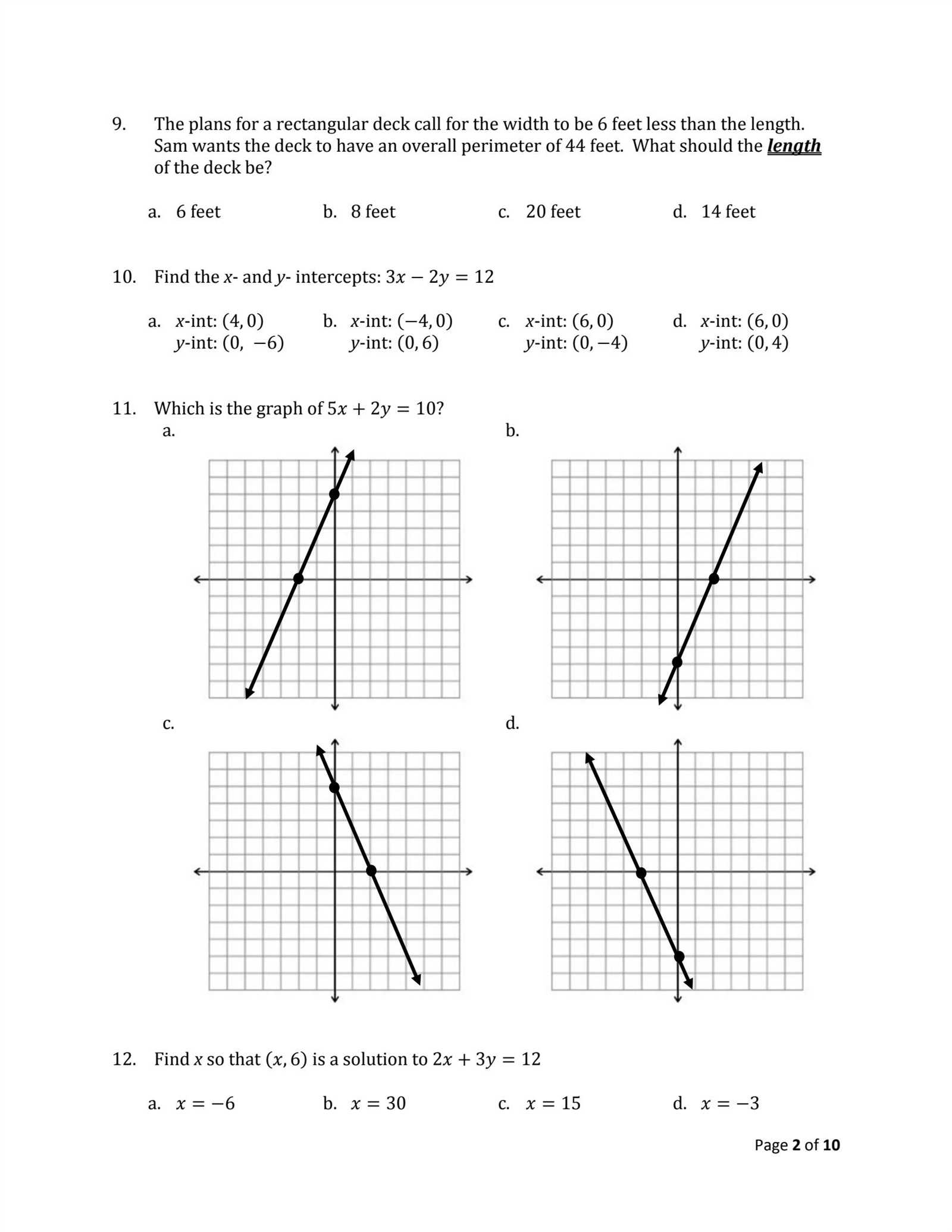
- Double-check your work: Review your calculations to catch any mistakes before finalizing your solution.
Common Mistakes to Avoid

Even with a strong understanding of the material, students can still fall into certain traps. Avoiding these common pitfalls can help ensure better results:
- Misinterpreting the problem’s requirements or missing key information.
- Forgetting to simplify the answer or leave it in its simplest form.
- Rushing through calculations without checking for errors.
- Overlooking negative signs or misplacing parentheses in equations.
By following these strategies and staying mindful of common mistakes, you’ll be better equipped to approach mathematical problems with confidence and accuracy, improving your overall performance in assessments.
Understanding Key Mathematical Concepts
To successfully navigate through complex mathematical problems, a solid grasp of fundamental principles is essential. Recognizing patterns and mastering core techniques will enable you to solve a variety of problems with greater ease. This section focuses on the most important concepts that form the foundation for solving a wide range of mathematical challenges.
Essential Topics to Master
Before tackling advanced problems, ensure you’re comfortable with these critical concepts:
- Linear Equations: Understanding how to solve equations involving variables is crucial for many problem types.
- Polynomials: Learn how to work with polynomial expressions, including factoring and simplifying.
- Functions: Recognize how to identify and evaluate functions, which play a central role in algebraic problem-solving.
- Inequalities: Solving inequalities is a key skill that can help with a wide range of problems.
Building Strong Problem-Solving Skills
Having the theoretical knowledge is important, but applying it effectively is equally essential. Here are a few ways to improve your problem-solving skills:
- Practice regularly to familiarize yourself with different problem types.
- Work on problems that involve multiple concepts, as this will help improve your ability to connect ideas.
- Review the steps of solutions and try to understand the reasoning behind each part of the process.
Mastering these key concepts will provide you with the tools necessary to approach problems confidently and accurately, setting the stage for success in more complex challenges.
Tips for Efficient Problem Solving
Effective problem solving is more than just applying formulas; it’s about using a methodical approach that allows you to break down complex issues into manageable steps. Adopting the right techniques can drastically improve your efficiency and accuracy, helping you work through challenges faster while minimizing mistakes.
Key Strategies to Improve Efficiency
To tackle problems more effectively, consider the following strategies:
- Understand the Problem Fully: Before jumping into calculations, take a moment to analyze the question. Identify what’s being asked and what information is provided.
- Work in Steps: Break down the problem into smaller, logical steps. This can prevent errors and make it easier to follow the solution process.
- Check for Simpler Methods: Look for ways to simplify the problem, whether it’s factoring, combining like terms, or identifying patterns that can speed up your work.
- Use Estimation: When dealing with complex calculations, estimate the result first. This helps ensure that your final answer is reasonable.
Common Mistakes to Avoid
While solving problems quickly is important, it’s equally essential to avoid common pitfalls that can lead to incorrect solutions. Here are a few mistakes to be mindful of:
- Rushing Through Steps: Moving too fast can lead to missing crucial details or making calculation errors. Always ensure you understand each step before proceeding.
- Overcomplicating the Problem: Don’t assume that every problem requires a complicated solution. Look for opportunities to simplify.
- Skipping Reviews: Always double-check your work before finalizing your solution. Small mistakes can have a significant impact on your results.
By following these tips and practicing consistently, you’ll be able to solve problems with greater efficiency, enhancing both your speed and accuracy.
Common Mistakes to Avoid on Exams

Even with a solid understanding of the material, certain errors can slip through during an assessment. These mistakes often arise from rushing, misinterpreting questions, or overlooking key details. Recognizing and avoiding these common pitfalls can significantly improve your performance and help you achieve more accurate results.
Typical Errors Students Make
Here are some frequent mistakes that can hinder your progress during an assessment:
- Misreading the Question: Skipping over important instructions or failing to understand exactly what is being asked can lead to incorrect solutions.
- Forgetting to Simplify: Often, students forget to simplify their answers before submitting them, leaving their final responses incomplete or incorrect.
- Overlooking Negative Signs: A common mistake is to miss negative signs in calculations, which can dramatically alter the outcome of an equation.
- Not Double-Checking Work: Failing to review calculations for simple errors, such as arithmetic mistakes or incorrect variable placement, can result in avoidable errors.
How to Prevent These Mistakes
Taking steps to address these issues can help you minimize errors and perform better on assessments:
- Read Each Question Carefully: Take your time to understand each question fully, paying attention to every detail.
- Work Methodically: Break down complex problems into smaller parts and check your work as you go.
- Practice Time Management: Allocate time for each section to avoid rushing and ensure you can double-check your answers at the end.
By being mindful of these common mistakes and incorporating strategies to avoid them, you’ll enhance your ability to tackle problems with confidence and accuracy.
How to Prepare for Mathematical Assessments
Effective preparation is key to performing well on any mathematical assessment. Simply reviewing notes isn’t enough–strategic practice, understanding core concepts, and honing problem-solving techniques are essential steps in ensuring success. This section provides practical steps you can take to be well-prepared when test day arrives.
The first step is to identify areas where you may need additional practice. Focus on concepts that are challenging and need more attention. Rather than just memorizing formulas, strive to understand how and why they work. This deeper understanding will make it easier to apply them effectively in different problem scenarios.
Another critical part of preparation is practicing with different types of problems. Working through a variety of questions–ranging from basic to more complex–helps you become familiar with how problems are structured and what techniques to use in different situations. Consistent practice will increase both your speed and accuracy, giving you more confidence during the actual assessment.
Essential Formulas for Mathematical Assessments

Mastering key formulas is crucial for tackling a wide range of problems in any mathematical assessment. Knowing when and how to apply these formulas can significantly improve your efficiency and accuracy. Below are some essential equations and rules that every student should be familiar with to succeed.
Quadratic Formula: Used to solve quadratic equations of the form ax² + bx + c = 0, the quadratic formula is:
x = (-b ± √(b² – 4ac)) / 2a
Distance Formula: This formula helps calculate the distance between two points, (x₁, y₁) and (x₂, y₂), on a coordinate plane:
d = √((x₂ – x₁)² + (y₂ – y₁)²)
Slope Formula: To find the slope of a line between two points, (x₁, y₁) and (x₂, y₂):
m = (y₂ – y₁) / (x₂ – x₁)
Point-Slope Form: This formula represents the equation of a line when the slope and a point on the line are known:
y – y₁ = m(x – x₁)
Exponential Growth/Decay Formula: This is used for problems involving population growth, radioactive decay, or interest calculations:
A = P(1 + r/n)^(nt) (for growth) or A = P(1 – r/n)^(nt) (for decay)
Familiarizing yourself with these formulas and understanding their applications will provide you with the tools needed to handle various types of problems effectively and efficiently.
Step-by-Step Guide to Problem Solving
Effective problem solving requires a structured approach that breaks down complex challenges into manageable steps. Following a logical sequence not only simplifies the process but also reduces the chances of making mistakes. In this guide, we outline a step-by-step method to help you tackle problems systematically and efficiently.
Step 1: Understand the Problem
Before diving into calculations or solutions, take time to fully understand the problem. Identify what is being asked and what information is provided. Look for key variables, constants, and relationships. The more clearly you understand the problem, the easier it will be to find the correct solution.
Step 2: Plan Your Approach
Once you have a clear understanding of the problem, plan how to approach it. Decide on the most appropriate methods or formulas to use. Determine whether the problem requires solving an equation, graphing, or applying a specific mathematical rule. Having a clear plan will help you work through the problem more efficiently.
Step 3: Solve the Problem
Now that you have your approach, begin solving the problem step by step. Take your time and follow each step carefully. If necessary, break down the problem into smaller parts to make it easier to handle. Be mindful of common mistakes such as arithmetic errors or overlooking important details.
Step 4: Check Your Work
Once you have arrived at a solution, double-check your work. Review each step to ensure there are no mistakes in your calculations or logic. If possible, substitute your solution back into the original equation to verify that it satisfies the conditions of the problem. This final check is crucial to confirm the accuracy of your solution.
By following these steps, you can approach any mathematical problem with confidence and clarity, reducing errors and improving your problem-solving skills.
Strategies for Tackling Word Problems
Word problems can often feel overwhelming due to their complex language and the need to translate real-world situations into mathematical expressions. However, by breaking down the problem and following a structured approach, you can solve them with confidence. Here are some strategies to help you approach word problems more effectively.
Steps to Solve Word Problems
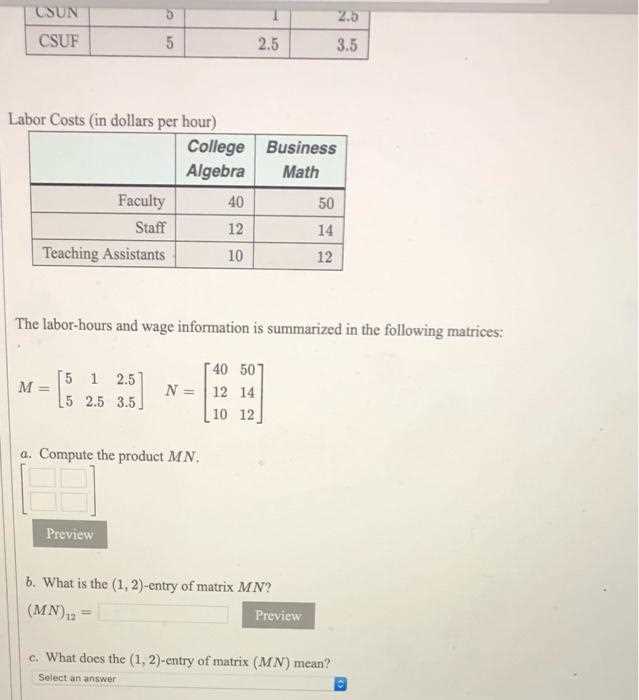
Follow these steps to simplify the process of solving word problems:
| Step | Description |
|---|---|
| 1. Read the Problem Carefully | Understand the context and the question being asked. Highlight key information such as numbers, units, and what you are solving for. |
| 2. Identify Variables | Determine what the unknowns are and assign variables to them. This helps in setting up equations. |
| 3. Translate Words into Equations | Convert the written information into a mathematical form, such as an equation or inequality. |
| 4. Solve the Equation | Use appropriate methods to solve for the unknowns. Ensure that you follow each step logically. |
| 5. Check Your Solution | Substitute the solution back into the original problem to verify that it makes sense and satisfies the conditions. |
Additional Tips for Success

- Draw Diagrams: When applicable, visualizing the problem with diagrams or charts can help clarify the relationships between different quantities.
- Look for Key Phrases: Certain phrases, like “total,” “difference,” or “rate,” often indicate specific operations that should be applied, such as addition, subtraction, or multiplication.
- Practice Regularly: The more you practice solving word problems, the more comfortable you’ll become with recognizing patterns and applying the right strategies.
By following these strategies, you’ll be better equipped to approach word problems methodically, improving both your problem-solving skills and your overall performance.
Time Management for Test Success
Effective time management is one of the most important factors when it comes to performing well in any assessment. Knowing how to prioritize your tasks, allocate enough time for each section, and maintain focus can significantly reduce stress and improve results. In this section, we’ll discuss how to manage your time efficiently leading up to the test and during the assessment itself.
Pre-Test Preparation
Planning your study schedule ahead of time is crucial for success. Without a clear plan, you may end up cramming or spending too much time on less important material.
- Create a Study Plan: Break down the material into manageable chunks. Set aside specific times for each topic, ensuring you cover all areas before the test.
- Prioritize Difficult Areas: Focus more on the topics you find most challenging. Spend extra time practicing problems or reviewing key concepts that need improvement.
- Use Time Blocks: Study in focused blocks of time (e.g., 25–45 minutes) with short breaks in between to maintain high concentration and avoid burnout.
Time Management During the Test
When it’s time to take the test, managing your time during the assessment is just as important as your preparation beforehand. Here are some strategies to help you stay on track:
- Skim Through the Entire Test: Quickly look over all the questions to get an idea of what to expect and gauge how long each section might take.
- Allocate Time for Each Section: If there are multiple sections, assign a set amount of time to each, and stick to it. Don’t get stuck on a single question for too long.
- Leave Time for Review: Try to finish the test with some time left over for review. Use this to check for mistakes, especially in calculations or wording.
By managing your time effectively both before and during the test, you’ll approach the challenge with a calm, organized mindset, allowing you to demonstrate your best performance.
How to Review Math Topics Effectively
Reviewing mathematical concepts effectively requires more than just reading through notes. It involves active engagement with the material, practicing problems, and understanding key principles. By focusing on the areas that need the most attention and applying the right strategies, you can maximize your review sessions and build confidence before your assessment.
1. Focus on Key Concepts
Start by identifying the core concepts that are most likely to appear in the assessment. Concentrate on areas that you find challenging or that have been emphasized in class. This targeted review helps ensure that you cover the most important material without wasting time on topics you already understand.
2. Practice Problems Regularly
Hands-on practice is one of the best ways to reinforce your understanding of mathematical concepts. Solve a variety of problems to ensure you can apply what you’ve learned in different contexts. Focus on different problem types, ranging from simple to more complex, to strengthen your problem-solving skills.
- Use Old Practice Tests: Look for past assessments or practice problems online to simulate test conditions.
- Work Through Mistakes: Review any mistakes made during practice and understand where you went wrong. This will help prevent similar errors in the future.
3. Create Summary Notes
Writing down key formulas, rules, and steps for solving problems can help reinforce your memory. Create concise summary notes or flashcards that you can quickly review. This allows you to consolidate information in a way that’s easy to revisit during your study sessions.
4. Test Yourself
After reviewing a topic, test yourself to gauge how well you understand it. Time yourself while solving problems to simulate the pressure of a real assessment. This will help you identify any weak spots and improve your ability to work under time constraints.
By incorporating these strategies into your review sessions, you can enhance your understanding and retention of key mathematical concepts, ensuring you are well-prepared for any challenge that comes your way.
Practice Questions for Mastery
To truly master any mathematical subject, consistent practice is essential. Engaging with a variety of problems allows you to test your understanding and sharpen your problem-solving abilities. In this section, we’ll provide practice questions that cover fundamental concepts and progressively become more complex, helping you solidify your knowledge and build confidence.
Basic Level Questions
Start with simpler problems to reinforce foundational concepts and ensure you have a solid grasp of the basics. These questions will help you identify and address any gaps in your understanding.
- Evaluate the expression: 5x + 3 when x = 2.
- Solve for x: 3x – 7 = 11.
- Factor the expression: x² + 5x + 6.
- Simplify the expression: 4(2x + 3) – 5x.
Advanced Level Questions
Once you feel comfortable with basic questions, move on to more challenging problems. These will test your ability to apply multiple concepts and work through complex steps.
- Solve for x: 2(x + 3) = 5x – 4.
- Factor the quadratic equation: x² – 4x – 21 = 0.
- Solve the system of equations: 2x + y = 10 and 3x – y = 4.
- Simplify the rational expression: (3x² – 5x + 2) / (x – 1).
By practicing these types of problems regularly, you will gain a deeper understanding of key concepts and improve your ability to solve more difficult challenges.
Understanding Graphs and Equations
In mathematics, understanding the relationship between graphical representations and their corresponding equations is crucial. Graphs provide a visual way to interpret mathematical problems, while equations offer a precise, algebraic method to describe these relationships. By mastering both, you can quickly analyze and solve problems that involve both numerical and geometric concepts.
Key Concepts of Graphs
Graphs serve as a visual tool that represents functions and equations. Each point on the graph corresponds to a specific solution of the equation. To interpret graphs effectively, it’s essential to understand the different types of graphs (linear, quadratic, exponential, etc.) and their key characteristics such as slope, intercepts, and curvature.
| Graph Type | Equation Form | Key Features |
|---|---|---|
| Linear | y = mx + b | Constant slope, straight line |
| Quadratic | y = ax² + bx + c | Parabolic curve, vertex |
| Exponential | y = ab^x | Rapid growth or decay, asymptote |
Connecting Graphs to Equations
Each equation has a corresponding graph that represents its solutions. To find the graph of an equation, you can plot key points, identify the shape, and analyze its behavior. Conversely, to derive an equation from a graph, you need to identify key features such as the slope, intercepts, and the general shape of the curve. This connection is essential when solving problems that require both algebraic manipulation and graphical interpretation.
By understanding how to move between graphs and equations, you can gain a deeper insight into the behavior of mathematical functions, making it easier to solve complex problems and apply theoretical knowledge in practical situations.
Breaking Down Complex Algebraic Expressions

When dealing with intricate expressions, breaking them down into manageable parts is essential for simplification and solving. This process often involves factoring, expanding, or combining like terms to reduce the complexity of the expression. Understanding how to approach these challenges step-by-step is key to mastering problem-solving techniques and obtaining accurate results.
Identifying Key Components
The first step in simplifying a complex expression is identifying the various components, such as constants, variables, and operators. Recognizing patterns, such as common factors or terms that can be grouped, is crucial in this process. It is also important to distinguish between terms that can be combined and those that cannot.
- Group similar terms (like 3x and 5x).
- Identify constants and isolate them from variable terms.
- Look for common factors or terms that can be factored out.
Applying Algebraic Techniques
Once the components are identified, algebraic techniques such as factoring, expanding, and simplifying can be applied. These techniques help reduce the complexity of the expression and make it easier to solve. Factoring, for example, involves rewriting the expression as a product of simpler terms, while expanding means distributing and multiplying terms to make the expression easier to work with.
- Factor expressions such as x² + 5x + 6 into (x + 2)(x + 3).
- Expand expressions like (x + 2)(x + 3) to x² + 5x + 6.
- Simplify expressions by combining like terms, such as 2x + 3x = 5x.
By carefully breaking down complex expressions and applying the appropriate algebraic methods, you can turn challenging problems into manageable ones and increase your ability to solve them accurately.
Handling Systems of Equations in Exams
When faced with systems of equations, the key to solving them lies in choosing the most effective method and applying it carefully. These types of problems often require solving multiple equations simultaneously, which can seem daunting. However, by breaking the system down into simpler steps and using the appropriate strategy, the solution process becomes more manageable. Whether you’re using substitution, elimination, or graphing, mastering these techniques is essential for success.
Choosing the Right Method
To efficiently solve a system of equations, it’s crucial to identify which method will work best for the given problem. Each approach has its advantages depending on the nature of the equations involved.
- Substitution method: Ideal for when one equation is easy to solve for a single variable.
- Elimination method: Works well when the coefficients of one of the variables are easily canceled out.
- Graphing method: Helpful for visualizing the solution where the two equations intersect on a graph.
Step-by-Step Approach to Solving
Once you’ve selected the appropriate method, follow these steps for a systematic approach to solving the system:
- Start by isolating one variable (if using substitution) or aligning the coefficients (if using elimination).
- Substitute or eliminate to solve for one variable.
- Plug the value back into one of the original equations to find the other variable.
- Check your solution by substituting both values into the remaining equation(s).
By mastering these techniques and understanding when to use each method, you’ll be able to handle systems of equations confidently and efficiently in any assessment scenario.
Common Algebraic Identities to Know
Understanding key mathematical identities is crucial for simplifying expressions and solving problems efficiently. These fundamental formulas are widely used to transform and simplify expressions, making them essential tools for anyone tackling problems involving variables, exponents, and polynomials. Familiarity with these identities will not only save time but also improve problem-solving accuracy.
Here are some of the most important identities that are frequently applied in a variety of mathematical contexts:
- Difference of Squares: ( a^2 – b^2 = (a – b)(a + b) )
- Perfect Square Trinomial: ( a^2 + 2ab + b^2 = (a + b)^2 )
- Sum of Squares (Complex Identity): ( a^2 + b^2 = (a + bi)(a – bi) )
- Binomial Expansion: ( (a + b)^n = a^n + binom{n}{1}a^{n-1}b + binom{n}{2}a^{n-2}b^2 + cdots + b^n )
- Quadratic Formula: ( x = frac{-b pm sqrt{b^2 – 4ac}}{2a} )
By recognizing and utilizing these identities, you can simplify and manipulate equations more easily. They help in factoring, expanding, and solving complex expressions, which are common tasks in mathematical problems. Mastering these identities is a step toward becoming proficient in solving a wide variety of problems.
Using Technology to Enhance Exam Prep
In today’s fast-paced world, technology plays an essential role in improving study habits and optimizing preparation for tests. With the right tools, you can streamline your learning process, access a wealth of resources, and track your progress in real-time. Embracing various technological solutions can help simplify complex concepts and provide interactive ways to practice problem-solving.
Here are some effective ways to incorporate technology into your study routine:
Interactive Learning Platforms
- Online Courses: Websites like Khan Academy, Coursera, and edX offer free lessons and practice exercises on a wide range of topics.
- Video Tutorials: YouTube channels provide step-by-step explanations of common problem types and tricky concepts.
- Study Apps: Mobile apps like Photomath and Wolfram Alpha allow you to scan and solve problems instantly, helping reinforce concepts as you practice.
Simulation and Practice Tools
- Practice Test Generators: Online tools let you create custom quizzes to assess your understanding and identify areas for improvement.
- Graphing Calculators: Tools like GeoGebra or Desmos provide interactive graphing capabilities, aiding in visualizing functions and solving equations.
- Timer Apps: Use apps that simulate timed conditions to practice under test-like pressure, improving your time management skills.
By incorporating these technologies into your study sessions, you can work smarter, not harder. They allow for better understanding, more effective practice, and a more personalized learning experience, which can lead to greater success in solving complex problems on the test.