Algebra Regents August 2025 Answers and Solutions

Preparing for a challenging exam requires more than just memorizing facts; it involves developing a deep understanding of the material. Whether you are tackling complex equations, solving problems, or analyzing mathematical concepts, effective preparation is crucial. By mastering the essential skills and knowing how to approach each question, you can boost your performance and improve your chances of success.

Comprehensive preparation is essential when approaching any major assessment. With the right strategies, you can confidently navigate through different types of questions, identify patterns, and apply logical reasoning. Knowing the typical question formats and understanding the methods required for solving them will help you feel more prepared on exam day.

Throughout this guide, you will find detailed solutions to some of the most common problem types, along with expert tips on how to maximize your study time. Whether you’re reviewing concepts or practicing timed exercises, this resource will provide the insights needed to approach the exam with confidence and clarity.

Algebra Regents August 2025 Answers

When preparing for a key mathematical examination, it’s crucial to focus on both problem-solving techniques and the ability to understand and apply various concepts. This section offers a comprehensive breakdown of common question types and the best strategies for tackling them. Whether you are familiar with the material or encountering it for the first time, understanding the structure of the test and knowing how to approach each question type can greatly enhance your performance.

Each problem type requires a unique approach, and being prepared with the right methods will allow you to efficiently find solutions. This section delves into step-by-step procedures to tackle typical exercises, ensuring that you not only solve them but understand the underlying principles. Through practice and familiarity with problem-solving techniques, you’ll be able to approach the exam with greater confidence and accuracy.

By examining the format of past assessments and reviewing the detailed solutions, you’ll gain valuable insights into how to handle similar questions. With a strategic approach and thorough understanding, you can navigate the test successfully and achieve your desired results.

Overview of the Algebra Regents Exam

Understanding the structure and expectations of a key mathematics assessment is essential for effective preparation. This examination is designed to evaluate your ability to apply mathematical concepts and solve various types of problems. The test includes a variety of question formats, each testing a specific set of skills ranging from basic calculations to complex reasoning and problem-solving abilities.

Test Structure and Content

The assessment is divided into multiple sections, with each focusing on different mathematical areas. It typically includes multiple-choice questions, short-answer problems, and extended response tasks. Each section requires a different approach, so familiarity with the question format is vital for success. Students must demonstrate both their procedural knowledge and their ability to explain their reasoning clearly.

Preparation Strategies

Successful preparation involves practicing with sample questions, reviewing key concepts, and familiarizing yourself with the test’s timing and format. Practicing under exam conditions helps build both speed and accuracy, two factors that are critical for completing the assessment efficiently. Additionally, developing a solid understanding of the core principles will allow you to tackle even the most challenging problems with confidence.

Key Topics Covered in August 2025

This assessment tests a wide range of essential mathematical skills, focusing on the application of fundamental concepts to solve problems. Each section of the test emphasizes different areas of mathematics, from basic operations to more complex problem-solving strategies. The key to success is understanding these topics thoroughly and being able to apply them effectively under timed conditions.

Core Mathematical Concepts

The test includes questions that assess your understanding of core mathematical principles such as functions, equations, and inequalities. Students are expected to solve problems that involve manipulating expressions, solving for unknowns, and interpreting mathematical relationships. Mastery of these fundamental concepts is crucial for answering a wide variety of questions confidently.

Problem-Solving and Critical Thinking

Another important area of focus is problem-solving, which involves analyzing real-world scenarios and applying mathematical reasoning to find solutions. These questions may require students to translate word problems into mathematical expressions, draw conclusions, and justify their answers. Being able to approach problems critically and logically is key to achieving success on the exam.

Understanding the Answer Format

Grasping the format in which your solutions are expected is crucial to performing well on any assessment. This test presents different types of questions that require various forms of responses. Understanding how to format your answers correctly can help you avoid unnecessary mistakes and ensure clarity in your explanations. Each question may require a brief response, a detailed solution, or a logical justification for your answer.

Multiple-Choice Questions

In some sections of the test, you will encounter multiple-choice questions where you select the correct option from several possibilities. These questions are designed to test your knowledge and understanding of key concepts. It is essential to carefully read the options and ensure that your selected answer directly addresses the question asked.

Open-Ended Responses

Other parts of the exam may ask for open-ended responses, where you must show your full work and explain how you arrived at your solution. For these questions, presenting a clear, step-by-step breakdown is necessary to demonstrate your thought process and justify your conclusion. A thorough explanation often carries more weight than a simple final answer, so clarity and logical progression are key.

How to Use Practice Tests Effectively

Practice tests are one of the most powerful tools to help you prepare for any exam. They provide a realistic preview of the test environment and allow you to familiarize yourself with the types of questions you will encounter. More importantly, they help identify areas where you need improvement and refine your time-management skills. Using practice exams strategically can significantly enhance your preparation and boost your confidence on test day.

Maximizing the Benefits of Practice Tests

To get the most out of practice tests, it’s essential to follow a structured approach:

• Start early: Begin taking practice tests well in advance of the exam date. This will give you ample time to review and focus on weaker areas.
• Simulate exam conditions: Take the practice tests under timed conditions to mirror the pressure of the actual exam. This will help you improve both your pacing and focus.
• Analyze your mistakes: After each test, carefully review your incorrect answers to understand why you made those mistakes and how to avoid them in the future.
• Track your progress: Regularly assess your performance to see how you are improving over time and where you still need to put in more effort.

Common Pitfalls to Avoid

While practice tests are incredibly helpful, there are some common mistakes that can hinder your progress:

1. Rushing through questions: Don’t rush your answers just to finish the test quickly. Focus on accuracy first.
2. Skipping reviews: Simply taking a test without reviewing your results misses a key opportunity for improvement.
3. Ignoring patterns: Pay attention to recurring mistakes across tests, as they often highlight areas that need deeper understanding.

Common Mistakes to Avoid During the Exam

When taking a challenging exam, it’s easy to make small errors that can cost valuable points. These mistakes often stem from rushing, misunderstanding the question, or overlooking important details. Being aware of these common pitfalls and taking steps to avoid them can greatly improve your performance. Here are some of the most frequent mistakes students make and how to prevent them.

Rushing Through Questions

One of the most common errors is rushing through the questions without carefully reading them. It’s tempting to move quickly, especially when you feel pressed for time, but this often leads to misinterpreting the problem or missing important information. Always take a moment to read each question thoroughly before attempting to solve it. If time allows, review your answers to ensure you didn’t overlook any key details.

Neglecting to Show Work

Another mistake is neglecting to show your work when required. Even if you know the correct answer, failing to document the steps you took to reach it can result in losing points. Many assessments value the process and reasoning, not just the final result. Taking the time to clearly present your thought process will demonstrate your understanding and improve your chances of earning full credit.

Step-by-Step Solutions for Practice Problems

Breaking down complex problems into manageable steps is key to mastering any mathematical concept. By following a structured approach, you can tackle even the most challenging questions with confidence. This section provides detailed, step-by-step solutions for common practice problems, helping you understand the logic behind each solution and improving your problem-solving skills.

Step 1: Understand the Problem

The first step in solving any problem is to thoroughly understand what is being asked. Read the question carefully and identify the key elements. What are you solving for? What information is provided? Once you have a clear understanding, you can move on to the next step.

Step 2: Set Up the Equation

After understanding the problem, the next step is to set up the equation or expression needed to solve it. Write down all relevant variables and constants, and translate the problem into a mathematical form. Be sure to include all given information, as missing details can lead to incorrect solutions.

Step 3: Solve the Equation

Once the equation is set up, begin solving it step by step. Perform necessary operations such as simplifying terms, factoring, or isolating variables. Take your time to ensure each step is correct, as errors at this stage can carry over to the final solution.

Step 4: Verify Your Answer

After reaching a solution, it’s important to verify your answer. Check if it makes sense within the context of the problem. You can also substitute your solution back into the original equation to ensure it satisfies all conditions. This step is crucial for avoiding mistakes and ensuring the accuracy of your result.

By following these steps, you will improve your ability to solve problems efficiently and with greater confidence, laying the foundation for success in the exam.

Tips for Efficient Time Management

Effective time management is one of the most critical skills when preparing for an exam. By organizing your study time and pacing yourself during the test, you can ensure that you tackle every question with confidence and avoid unnecessary stress. With proper planning and strategy, you can maximize your performance while minimizing the risk of running out of time.

Here are several time management tips to help you succeed:

• Plan Ahead: Start your preparation well in advance of the exam date. Break your study sessions into manageable chunks and allocate specific times for each topic or section.
• Set Time Limits: During your practice, set strict time limits for each section to simulate exam conditions. This will help you build speed and become accustomed to the time constraints you’ll face during the actual test.
• Prioritize Questions: On exam day, read through all the questions first and tackle the ones you feel most confident about. This strategy allows you to score easier points quickly and reduces the pressure for tougher questions later.
• Don’t Get Stuck: If you find yourself struggling with a question, move on and come back to it later. Spending too much time on one problem can hurt your overall performance, especially if you miss out on easier questions.
• Use the Last Few Minutes Wisely: If time allows at the end, use the final minutes to review your answers. Double-check for any careless mistakes or unanswered questions, but avoid redoing problems you’ve already completed.

By implementing these strategies, you can manage your time effectively during both your study sessions and the exam itself, leading to a more organized, confident, and successful performance.

Mastering Mathematical Concepts for Success

To excel in any exam, it is essential to have a strong understanding of core mathematical concepts. Mastering the foundational principles not only boosts confidence but also improves problem-solving efficiency. The ability to apply these concepts in a variety of situations is key to achieving success, as it allows you to approach even the most complex problems with clarity and precision.

Key Concepts to Focus On

Focus on strengthening the following essential areas to ensure success:

• Equations and Inequalities: Understand how to manipulate and solve equations, including linear, quadratic, and rational expressions. Be sure to practice both simple and complex equations to build flexibility in solving various types of problems.
• Functions and Graphs: Familiarize yourself with different types of functions, such as linear and exponential, and their graphical representations. Learn how to interpret and draw graphs based on equations.
• Polynomials: Practice operations with polynomials, including addition, subtraction, multiplication, and factoring. Recognize the importance of factoring in simplifying expressions and solving equations.
• Systems of Equations: Work on solving systems of equations using substitution, elimination, and graphical methods. Mastering these techniques will help you efficiently solve more advanced problems.
• Word Problems: Develop skills in translating word problems into mathematical expressions. Breaking down real-life scenarios into solvable steps is a crucial aspect of success in any exam.

Strategies for Strengthening Your Understanding

To ensure a deep understanding of these concepts, follow these strategies:

1. Practice Regularly: Consistent practice is the key to mastering any skill. Set aside time each day to work through problems, review concepts, and track your progress.
2. Understand, Don’t Memorize: Focus on understanding the “why” behind each concept rather than just memorizing formulas. This deeper understanding will help you apply your knowledge in various contexts.
3. Seek Help When Needed: Don’t hesitate to ask for clarification or assistance if you’re struggling with certain concepts. Teachers, tutors, or study groups can provide valuable insights.
4. Use Multiple Resources: Utilize a variety of study materials, such as textbooks, online resources, and practice tests, to gain a broader perspective on each topic.

By focusing on these key concepts and employing effective strategies, you’ll be well-prepared to tackle any challenges and achieve success in your mathematical exams.

How to Review Your Mathematical Skills

Reviewing mathematical concepts effectively is essential for reinforcing your understanding and ensuring readiness for any assessment. It’s not just about memorizing formulas; it’s about practicing techniques, identifying weaknesses, and consistently testing your knowledge to build confidence. A structured review approach can help you solidify your skills and tackle problems with ease.

Steps for Reviewing Your Skills

To review your skills effectively, follow these steps:

• Start with the Basics: Ensure that you have a solid understanding of foundational concepts. Go over fundamental operations such as solving equations, manipulating expressions, and understanding inequalities. Mastering these basics will make more advanced topics easier to tackle.
• Work Through Practice Problems: The best way to review is through hands-on practice. Solve a variety of problems, from simple to complex, to ensure you’re comfortable with all types of questions. Focus on areas where you find the most difficulty.
• Review Mistakes: When you make an error, take the time to understand why it happened. Analyze your mistakes and try to find alternative methods to solve the problem correctly. This will help you avoid repeating the same mistakes.
• Use Online Resources: Take advantage of online tools and practice tests to reinforce your learning. Many websites offer interactive problems, video tutorials, and explanations that can help clarify difficult concepts.

Additional Tips for Effective Review

To maximize your review time, consider the following tips:

1. Set a Schedule: Set aside dedicated time each day for review. Consistent, short study sessions are often more effective than cramming at the last minute.
2. Focus on Weak Areas: Identify the topics that you struggle with the most and prioritize those during your review sessions. Give yourself time to master these areas before moving on to easier material.
3. Study in Groups: Collaborate with peers to discuss challenging problems and solutions. Group study can offer different perspectives and help reinforce your learning through discussion.
4. Take Breaks: Give yourself regular breaks during study sessions. Short breaks can improve focus and prevent burnout, ensuring you remain productive throughout your review.

By following these steps and tips, you can effectively review your skills, gain confidence, and improve your performance on any exam. Regular practice and a focused approach will ensure that you’re well-prepared to succeed.

Breaking Down Complex Mathematical Problems

Complex mathematical problems can seem intimidating at first glance, but with the right approach, they become manageable. The key is to break down the problem into smaller, more manageable parts. By identifying the structure of the problem and systematically addressing each component, you can simplify even the most complicated equations and expressions.

Start by analyzing the problem step by step. Recognize the different elements involved, such as variables, constants, and operations. Then, apply logical reasoning and mathematical rules to solve each part. This approach not only makes solving the problem easier but also helps you develop a deeper understanding of the underlying concepts.

Steps to Simplify Complex Problems

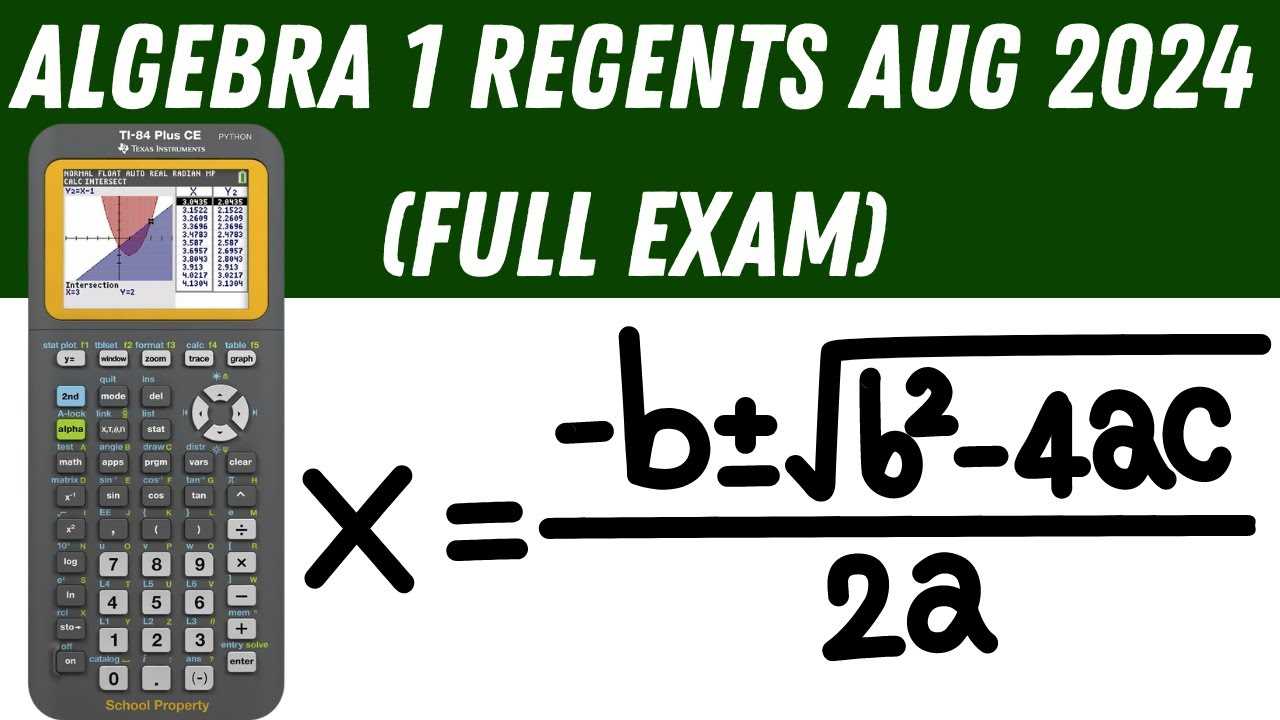
Follow these steps to effectively break down and solve challenging mathematical problems:

• Identify the Known and Unknown: Begin by clearly identifying what information is given and what needs to be found. This will help you focus on the relevant parts of the problem.
• Break the Problem into Smaller Parts: Divide the problem into manageable sections. Tackle each section one at a time instead of trying to solve the entire problem at once.
• Look for Patterns: In many cases, complex problems contain patterns that can simplify the process. Identify these patterns to predict the next steps or simplify the calculations.
• Use Substitution or Elimination: For problems involving multiple equations or unknowns, substitution or elimination methods can help simplify the system of equations and make solving easier.
• Check Your Work: After solving each part, check your calculations and ensure that the steps are logical. This helps prevent errors and ensures accuracy in the final solution.

Approaching Word Problems

Word problems often appear more complicated due to the extra layer of interpretation required. To break down word problems effectively:

• Extract Key Information: Carefully read the problem and underline or highlight the key information, such as numbers, relationships, and what is being asked.
• Translate to Mathematical Expressions: Convert the text into mathematical terms. For example, if the problem mentions “a number increased by five,” represent it as x + 5.
• Set Up the Equation: Based on the information and relationships, set up an equation that represents the situation described in the word problem.
• Solve and Interpret: Once you solve the equation, make sure to interpret the solution in the context of the original problem to ensure it makes sense.

By following these strategies, you can approach even the most complex problems with confidence and ease, breaking them down into manageable parts and applying logical methods to reach the solution.

Resources for Further Study and Preparation

In order to improve understanding and master challenging concepts, it’s important to use a variety of resources during your preparation. These tools can offer additional explanations, examples, and practice opportunities that can help solidify your knowledge. From textbooks and online platforms to practice tests and video tutorials, there are plenty of materials available to assist with your studies.

Utilizing diverse resources ensures that you get a well-rounded understanding of the subject and can approach each topic from different angles. The following resources can enhance your study sessions and help you perform confidently in assessments.

Books and Textbooks

Books and textbooks provide in-depth coverage of topics and step-by-step instructions. They are often written by experienced educators and contain exercises designed to reinforce concepts.

Title	Author	Focus Area
“Math Success”	John Doe	Problem-solving techniques, equations
“Mastering Mathematical Concepts”	Jane Smith	Foundational theory, practice exercises
“Advanced Problem Solving”	Mark White	Complex concepts and strategies

Online Resources

There are many online platforms that offer interactive lessons, tutorials, and practice tests. These websites allow you to study at your own pace and track your progress over time.

• Khan Academy: Offers free video tutorials and practice exercises on a wide range of topics.
• Wolfram Alpha: A computational engine that helps with solving problems step-by-step.
• Brilliant: Provides interactive problem-solving experiences that help deepen your understanding of mathematical principles.
• Quizlet: Features study sets and flashcards created by other users to assist with memorizing key concepts.

By integrating these resources into your study routine, you can strengthen your comprehension, identify weak spots, and boost your confidence. Consistent practice using these tools will enhance your skills and increase your chances of success.

How to Approach Word Problems in Algebra

Word problems can often seem challenging because they require translating real-world situations into mathematical expressions. The key to solving these problems is breaking them down into smaller, manageable steps and carefully identifying the variables and relationships involved. With a clear strategy, word problems become more approachable, and the solutions easier to find.

To effectively solve word problems, it’s important to follow a systematic approach. Below are some steps to guide you through the process:

1. Read the Problem Carefully: Understand the situation being described and identify the key pieces of information. Pay attention to any numbers, units, and keywords that indicate mathematical operations (e.g., total, difference, product).
2. Define the Variables: Choose variables to represent the unknowns. Label them clearly so you can track what each variable represents.
3. Translate into Mathematical Expressions: Convert the information from the word problem into an equation or set of equations. Use the appropriate mathematical operations for the relationships described in the problem.
4. Set Up and Solve the Equation: Once you have the equation, solve for the unknown. This may involve isolating variables, simplifying expressions, or using other mathematical techniques.
5. Check the Solution: After solving, check your answer to ensure it makes sense in the context of the problem. Make sure it answers the question posed and is consistent with the information provided.

By following these steps, word problems become more straightforward, and you can systematically work through even the most complex scenarios. Practice with a variety of problems to improve your ability to identify key information and set up equations effectively.

Below is an example of how to approach a typical word problem:

• Example: A store sells pencils in packs of 12. If a customer buys 5 packs, how many pencils does the customer purchase in total?
• Solution Steps:
• Define the variable: Let x represent the number of pencils.
• Translate the problem: Since each pack contains 12 pencils, and 5 packs are purchased, the total number of pencils is x = 5 × 12.
• Solve the equation: x = 60.
• Conclusion: The customer purchases 60 pencils in total.

By applying this method consistently, you’ll be able to tackle word problems more efficiently and accurately.

Best Strategies for Multiple-Choice Questions

Multiple-choice questions can be tricky, but with the right approach, you can significantly improve your chances of selecting the correct answer. These questions often test not only your knowledge but also your ability to apply logical reasoning under time pressure. Developing effective strategies can help you navigate through these questions with greater confidence and accuracy.

Here are some essential strategies for tackling multiple-choice questions:

Strategy	Description
Read Carefully	Always read the question and all answer choices carefully. Sometimes, small details in the wording can be crucial in determining the correct answer.
Eliminate Incorrect Options	Eliminate any answer choices that are obviously incorrect. This increases your chances of selecting the right answer by narrowing down the options.
Look for Clues	Sometimes, the question or the other answer choices provide subtle hints. For example, look for patterns or language that can guide you toward the correct solution.
Guess Strategically	If you’re unsure, make an educated guess based on the process of elimination and any knowledge you have about the topic. If two answers seem similar, there’s often a good reason to lean toward one.
Time Management	Don’t spend too much time on any one question. If you’re stuck, move on and return to it later. Keeping track of time ensures you can attempt all questions.

By implementing these strategies, you will be better equipped to answer multiple-choice questions efficiently and correctly. Regular practice with these techniques will help you develop a sharper intuition for choosing the right answers under test conditions.

Improving Test-Taking Confidence

Confidence plays a crucial role in performing well on any exam. The way you approach the test, your mindset, and your preparation habits can all impact how comfortable and assured you feel during the actual test. Building self-confidence is not just about knowing the material; it’s also about developing strategies that help you manage stress and stay focused under pressure.

One effective way to boost confidence is through consistent practice. The more familiar you are with the types of questions and problems you will face, the less anxious you will feel on test day. Additionally, mastering time management and understanding how to tackle difficult questions can also make a significant difference in how you approach the test.

Another key factor is mental preparation. Take time to relax before the exam, get enough rest, and maintain a positive outlook. By focusing on what you know and avoiding negative thoughts, you can create a mental state that promotes success.

Finally, remember that mistakes during practice are part of the learning process. Use them as opportunities to improve rather than as signs of failure. Confidence grows when you learn from setbacks and continue to build on your strengths.

What to Expect on Exam Day

On the day of the test, it’s important to approach the experience with a sense of preparedness and calm. Knowing what to expect can significantly reduce stress and help you stay focused. The exam environment will be structured to allow you to demonstrate your knowledge and problem-solving skills, so being mentally and physically ready is key to performing your best.

Upon arrival, you will be directed to your assigned seat. It’s important to bring all necessary materials, such as identification, pencils, and any permitted tools. Be sure to review the specific guidelines provided for the test, as there may be rules about what is allowed in the testing area. You will likely be given a specific amount of time to complete the exam, with regular instructions on how to proceed and manage your time.

As you begin the test, take a few moments to read through the instructions carefully. Make sure you understand the structure of the exam, including how to answer each section, and what to do in case you need more time or assistance. It’s normal to feel nervous at the start, but remember that staying calm and focused will help you complete each task efficiently.

Throughout the exam, manage your time wisely. If you find a question challenging, move on and return to it later. Don’t dwell too long on any single problem–maintain a steady pace. Most importantly, trust in your preparation and approach the exam with confidence.