
Understanding the core principles behind solving mathematical challenges is essential for building a strong foundation in problem-solving. Whether you’re tackling complex equations or interpreting relationships between variables, grasping these concepts is crucial for success.
In this section, we’ll guide you through different types of problems, providing effective strategies for approaching and solving them with clarity and precision. You’ll learn how to break down complicated problems into manageable steps, helping you not only achieve the correct results but also develop a deeper understanding of the underlying principles.
Practice is key to mastering these skills. By working through examples and refining your techniques, you’ll gain confidence in your ability to tackle various mathematical challenges efficiently. Whether for academic tests or real-world applications, this knowledge will equip you to handle a wide range of scenarios with ease.
Understanding Inequalities in Mathematics
Mathematics involves comparing different quantities to identify their relationships and order. This comparison often requires methods to express how one value is greater than or less than another. These fundamental concepts are used across various problems to determine possible solutions and evaluate different scenarios.
At its core, this area of study focuses on expressing the limits within which certain values or variables can exist. This can range from simple comparisons between two numbers to more complex statements involving multiple variables. The goal is to understand the range of possible outcomes and determine whether they satisfy certain conditions or restrictions.
By developing a solid understanding of these mathematical principles, students gain the ability to approach more advanced topics with confidence. Whether analyzing relationships in algebraic expressions or solving real-world problems, the skills learned in this area form a critical part of any mathematician’s toolkit.
Key Concepts in Solving Inequalities
In mathematical problem-solving, it is essential to understand the relationships between different values and how to express them within specific limits. Mastering this involves recognizing patterns and applying logical steps to find the range of possible solutions. These techniques are foundational in various fields, including algebra and calculus.
One of the core principles is the manipulation of expressions to isolate the unknown variable. Whether working with linear, quadratic, or more complex expressions, it is important to apply rules systematically. Operations such as addition, subtraction, multiplication, and division help refine the relationship and reveal the potential values for the variable.
Critical thinking plays a significant role in interpreting the results. It’s crucial to check the validity of the solution by reviewing the constraints and ensuring that all steps follow mathematical principles. Additionally, recognizing when to flip the inequality sign during multiplication or division by negative numbers is vital for accurate solutions.
By developing a clear understanding of these key concepts, you gain the ability to handle a variety of mathematical challenges and ensure the correct evaluation of different expressions. This knowledge is not only valuable in academic settings but also useful in solving real-world problems.
Common Types of Inequality Questions
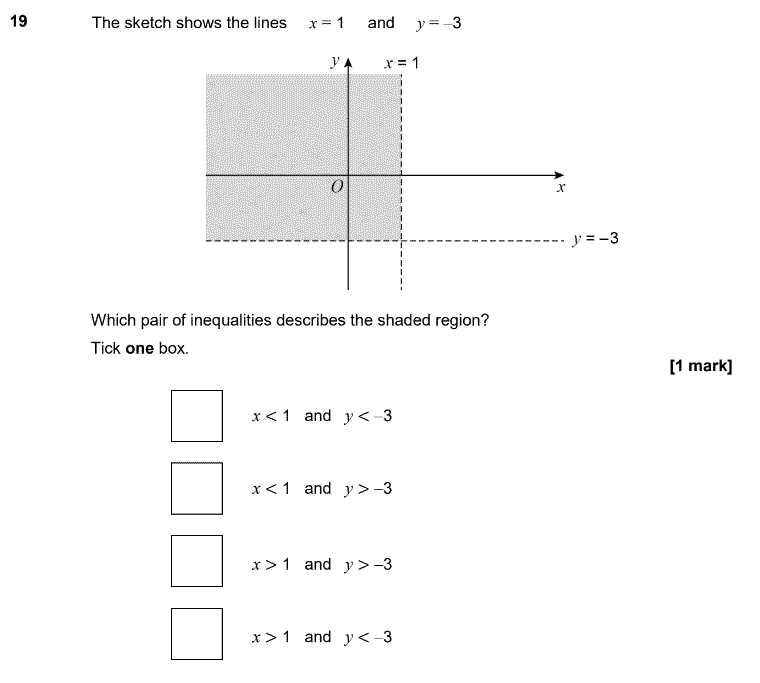
When solving mathematical problems involving comparisons, different types of scenarios require specific methods and techniques. These problems often vary in complexity and structure, but understanding the key patterns can significantly improve problem-solving skills. Recognizing the type of comparison is the first step toward choosing the right approach for finding the solution.
One common scenario involves linear expressions, where the goal is to determine the range of values that satisfy a particular condition. These problems often require basic operations such as addition, subtraction, multiplication, or division to isolate the variable and find the correct solution set. Another common type involves quadratic expressions, where the relationship between the terms introduces additional complexity, requiring more advanced techniques like factoring or completing the square.
Compound relationships also frequently appear, where multiple conditions are combined into a single problem. These require breaking down the problem into smaller, more manageable steps and solving each part separately before finding the overall solution. Lastly, problems involving absolute values often require special attention to both positive and negative scenarios, as these introduce additional constraints that must be considered carefully.
By becoming familiar with these various types of mathematical challenges, students are better equipped to handle a broad range of problems and develop strategies for efficient and accurate solutions.
Step-by-Step Problem Solving
Approaching mathematical challenges systematically is essential for finding the correct solution. Breaking down a problem into clear, logical steps makes it easier to understand and solve. The process involves manipulating expressions, isolating variables, and interpreting the results in a way that satisfies the given conditions.
The first step in solving such problems is identifying the type of comparison being made. Once that is clear, you can apply the necessary operations to simplify the problem. This often involves adding, subtracting, multiplying, or dividing both sides of the equation to isolate the unknown value. At times, more complex transformations like factoring or substitution may be required.
After simplifying the expression, it’s important to check for any special conditions, such as flipping the comparison sign when multiplying or dividing by negative numbers. Once these steps are completed, double-check the solution to ensure it fits within the defined limits. Verifying the result helps confirm that all steps were followed correctly and that the final solution is valid.
By following a methodical approach and practicing regularly, you can confidently solve a wide range of problems and ensure accurate, reliable results every time.
How to Graph Inequalities

Visualizing mathematical relationships can make it easier to understand and solve complex problems. Graphing is an effective method for representing comparisons between variables, helping to identify the range of possible solutions. When graphing, it is important to consider both the type of expression and the constraints involved to ensure accuracy.
Understanding the Graphing Process

To graph a mathematical relationship, follow these steps:
- Start by isolating the variable on one side of the expression if necessary.
- Identify the type of graph: Is it a straight line, curve, or shaded region?
- Plot the boundary of the solution, using a solid or dashed line to indicate whether the boundary is included or excluded.
- Determine which side of the boundary the solution set lies on, and shade that region.
Key Considerations When Graphing
- If the comparison includes a “greater than” or “less than” symbol (), use a dashed line to indicate that the boundary is not included in the solution set.
- If the comparison includes a “greater than or equal to” or “less than or equal to” symbol (≤, ≥), use a solid line to show that the boundary is part of the solution.
- Check the direction of shading. The solution region is typically above or below the line, depending on the inequality’s sign.
Graphing these relationships allows for a clearer visual understanding, making it easier to identify which values satisfy the given conditions.
Real-Life Applications of Inequalities
Mathematical comparisons are not just confined to textbooks; they are used in many practical situations in everyday life. From budgeting to engineering, understanding how different values relate to one another can help solve real-world problems efficiently. These concepts allow individuals and professionals to make informed decisions and optimize outcomes in various fields.
One common application involves budgeting and finance. For example, a person may need to figure out how much they can spend on different categories without exceeding a specific budget limit. In business, inequalities are used to model profit margins, production limits, and resource allocation. Similarly, engineers use these principles to design structures that must meet certain safety or functional constraints.
The following table highlights some key real-life scenarios where mathematical comparisons are applied:
| Application | Example | Mathematical Concept |
|---|---|---|
| Personal Budgeting | Spending within a set amount | Greater than or less than comparison |
| Business | Maximizing profits while staying under costs | Linear relationships and constraints |
| Engineering | Ensuring materials meet safety standards | Limitations and boundary conditions |
| Transportation | Calculating maximum load capacity for vehicles | Capacity and weight comparisons |
By applying these mathematical techniques, individuals and businesses can make more effective decisions that balance constraints and maximize efficiency in a variety of situations.
Tips for Tackling Multiple Choice Questions
Multiple choice challenges can be tricky, especially when you’re dealing with complex comparisons or relationships between values. However, with the right approach, these types of problems can be solved efficiently. The key to mastering them lies in understanding the underlying principles and applying smart strategies to eliminate incorrect options quickly.
Effective Strategies for Solving
- Read Carefully: Always begin by reading the problem thoroughly to understand what is being asked. Pay attention to keywords and the relationships between variables.
- Eliminate Clearly Wrong Options: If you can immediately identify one or more options that are clearly incorrect, cross them out. This increases your chances of selecting the correct answer.
- Work Backwards: If you’re unsure about the solution, try plugging each answer choice into the original problem to see which one satisfies the conditions.
- Consider Special Cases: Be mindful of any special conditions in the problem (such as signs, limits, or boundaries) that could impact the correct answer.
Managing Time and Reducing Mistakes
- Time Management: Don’t spend too much time on any one question. If you’re stuck, move on and come back to it later.
- Check Your Work: If time permits, double-check your answers before submitting. Look for small errors, such as calculation mistakes or misinterpretation of the problem.
- Stay Calm: Multiple choice tests can be stressful, but staying focused and calm can help you think more clearly and make better decisions.
By applying these tips, you can approach multiple-choice problems with confidence, improving both speed and accuracy in finding the correct solution.
Solving Compound Inequality Problems
When dealing with problems that involve multiple conditions or restrictions, understanding how to approach compound situations is crucial. These problems typically require handling two or more relationships at once and finding a solution set that satisfies all the given conditions. The key to solving these problems is breaking them down into manageable steps and applying the correct logical rules to combine the results.
There are two main types of compound scenarios: “and” problems and “or” problems. In “and” problems, the solution must satisfy both conditions simultaneously, whereas in “or” problems, satisfying just one of the conditions is enough. Understanding the distinction between these two types will help you choose the right approach to find the solution.
Steps for Solving Compound Problems
- Separate the Conditions: Break the compound statement into its individual parts, ensuring you understand each condition separately.
- Solve Each Part: Solve each inequality independently, treating each condition as if it were a single problem.
- Combine the Results: For “and” problems, find the overlap of the solution sets. For “or” problems, combine all possible solutions.
- Check for Restrictions: Make sure that the solution respects any special conditions, such as excluding certain values or working with specific ranges.
Example of Solving Compound Problems
- If you have a problem such as “3
- For “3
- For “x + 5
- The final solution is the range -2
By following these steps and practicing regularly, you can handle compound problems with ease and find accurate solutions efficiently.
Understanding Systems of Inequalities

In many real-world scenarios, multiple conditions need to be satisfied at once. This often leads to problems involving more than one comparison at a time. When solving these types of problems, it’s important to understand how different constraints interact and how to find a solution that meets all conditions simultaneously. Systems that involve several of these comparisons are commonly used in optimization, economics, and other practical applications.
To solve these types of problems, the process generally involves analyzing each condition separately, then determining where the solution sets for all conditions overlap. The goal is to find a set of values that satisfies every condition in the system. This requires both logical reasoning and a solid understanding of how different relations can be combined.
In these problems, there are a few key steps that should be followed:
- Identify the Conditions: Start by clearly writing down each condition or constraint in the system.
- Solve Each Individual Condition: Solve each part of the system as if it were a separate problem. Treat each condition independently first.
- Find the Intersection: Once each condition is solved, find the overlap of all solution sets. The solution to the system will be the values that satisfy all conditions simultaneously.
- Check for Validity: Make sure the final solution satisfies all given restrictions and boundary conditions.
By following these steps, you can solve even complex problems that involve multiple constraints and find the most optimal solutions to real-world challenges.
How to Solve Rational Inequalities
When working with mathematical expressions that involve fractions, the process of solving them can be more complex due to the presence of variables in the denominator and numerator. Solving these types of problems requires careful manipulation of the expressions and a solid understanding of how to deal with restrictions on the variable. These problems often involve determining the values of the variable that make the overall expression either greater than or less than a particular threshold.
The key steps to solving rational inequalities involve first isolating the variable and then analyzing the critical points where the expression may change its sign. It’s important to remember that the solution set will not only depend on the values that satisfy the equation but also on any domain restrictions that prevent the denominator from being zero.
Here’s a general approach for solving these problems:
- Move all terms to one side: Start by getting all terms on one side of the inequality, leaving zero on the other side.
- Find critical points: Set the numerator and denominator equal to zero to find critical points. These are the values where the expression could change signs or become undefined.
- Analyze intervals: Use these critical points to divide the number line into intervals. Test the sign of the expression in each interval to determine where the inequality holds.
- Check for restrictions: Make sure that the values of the variable do not make the denominator zero, as this would lead to undefined expressions.
By following these steps and carefully analyzing each interval, you can successfully solve rational expressions and find the values that satisfy the given inequality.
Handling Absolute Value Inequalities
When dealing with expressions involving the absolute value of a variable, the approach to solving them can differ from typical problems. The absolute value represents the distance of a number from zero, meaning it always yields a positive result. Solving these problems requires understanding how to break the inequality into two separate cases based on the nature of the absolute value expression.
The key to solving these types of problems is recognizing that absolute value inequalities lead to two distinct scenarios. One where the expression inside the absolute value is greater than a positive number and one where it is less than a positive number. Each case requires a different strategy to solve, but both involve isolating the variable and considering both the positive and negative sides of the inequality.
Here’s the general approach to solving absolute value inequalities:
| Case | Step | Resulting Expression |
|---|---|---|
| Greater than | Split the inequality into two separate inequalities | Expression > Positive Number or Expression |
| Less than | Keep the inequality within bounds, solve for the range of values | Negative Number |
By considering both the positive and negative scenarios, you can determine the range of values that satisfy the inequality. In some cases, you may need to test the solution set to ensure that it meets all conditions, particularly when dealing with absolute value expressions that involve more complex relationships.
Working with Linear Inequalities
When solving problems involving linear relationships between variables, it’s important to understand how to manipulate expressions that include relational symbols such as “greater than” or “less than.” These problems often focus on finding the range of possible values for a variable that satisfy a particular condition, and they are foundational in fields like algebra and optimization.
In these problems, the process typically involves isolating the variable and performing algebraic operations just as you would with equations. However, there are additional rules to consider, especially when multiplying or dividing by negative numbers, as these operations can flip the direction of the relational symbol.
Here’s a general approach to solving linear inequalities:
- Isolate the variable: Start by simplifying the inequality, just like an equation. Move all terms involving the variable to one side and constant terms to the other.
- Perform operations: Apply addition, subtraction, multiplication, or division to simplify the inequality further. Remember that when dividing or multiplying by a negative number, the direction of the inequality symbol will change.
- Graph the solution: Once the variable is isolated, it’s often useful to represent the solution on a number line, showing all possible values that satisfy the condition.
By following these steps, you can effectively solve linear problems and understand the conditions that satisfy them. The key is careful manipulation of the inequality and being mindful of how each operation affects the solution set.
How to Interpret Word Problems
Word problems can initially seem daunting, especially when mathematical concepts are hidden within everyday situations. The key to solving these problems is breaking down the text into smaller, more manageable parts and translating the words into mathematical expressions. This involves identifying the relevant information, defining variables, and setting up an equation or relationship that represents the situation described.
The first step in tackling word problems is to read carefully and highlight the important details. Pay close attention to the quantities involved, the relationships between them, and any conditions or restrictions stated in the problem. Once the key information is identified, the next task is to translate the narrative into a mathematical form that can be solved.
Steps to Solve Word Problems
- Identify the variables: Determine what quantities are unknown and assign them variables, such as “x” or “y.”
- Translate the text: Convert the words into an equation or inequality. For example, if a problem mentions “the sum of two numbers,” you would write that as an addition equation.
- Set up the equation: Use the relationships provided in the problem to create a mathematical expression or system of equations.
- Solve and interpret: Solve the equation and check the solution to make sure it makes sense in the context of the problem.
Common Pitfalls to Avoid
- Misinterpreting relationships: Be careful not to confuse “more than” with “less than,” or “sum” with “difference.” Understanding the exact wording is crucial for setting up the correct equation.
- Overlooking constraints: Pay attention to any restrictions mentioned in the problem, such as “only positive numbers” or “a maximum value.” These conditions can impact the solution.
By following these steps and practicing regularly, you’ll improve your ability to decode word problems and apply mathematical methods to solve them effectively. The more you practice, the easier it will become to translate complex scenarios into solvable equations.
Identifying Key Mistakes in Solving Inequalities

When working with problems that involve relationships between variables, it’s easy to make errors that can lead to incorrect conclusions. These mistakes often stem from misunderstandings of fundamental rules or from simple miscalculations. Identifying these common errors early on can help you avoid frustration and improve your overall problem-solving skills.
One of the most frequent mistakes involves incorrectly handling operations that affect the direction of the relational symbol, such as multiplying or dividing by negative numbers. Another common issue is misinterpreting the conditions or forgetting to apply them properly during the solution process. Recognizing these pitfalls is crucial for successfully solving problems.
Common Errors and How to Avoid Them
- Flipping the relational symbol: When multiplying or dividing by a negative value, the direction of the relational symbol must be reversed. Forgetting this step is a frequent mistake that leads to incorrect solutions.
- Ignoring domain restrictions: Some problems come with constraints such as variables needing to stay positive. Failing to account for these limits can result in solutions that are not feasible.
- Incorrectly simplifying expressions: Simplification errors, such as misadding or subtracting terms, can cause a small mistake to escalate into a much larger error.
- Misunderstanding compound relationships: Problems that involve multiple conditions can be tricky. Overlooking how different parts of the problem are connected can lead to incomplete or wrong solutions.
How to Prevent Mistakes
- Double-check your work: After performing each operation, review your steps carefully to ensure they follow the correct rules.
- Practice with varied problems: The more you work on these types of problems, the better you’ll become at spotting mistakes and avoiding them.
- Understand the rules thoroughly: Make sure you have a solid grasp of the key principles, especially when it comes to reversing the direction of relational symbols or applying constraints.
By being aware of these common mistakes and practicing careful problem-solving, you can significantly improve your accuracy and confidence when working with mathematical relationships.
Practice Questions for Inequality Mastery
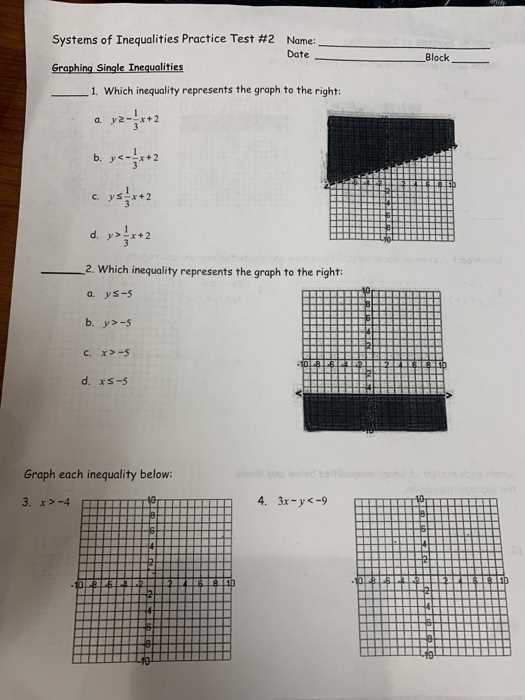
To truly master solving problems involving relational expressions, consistent practice is essential. Working through a variety of practice problems helps reinforce your understanding of key concepts and improves your ability to identify patterns and solutions. In this section, you’ll find a selection of problems designed to test and enhance your problem-solving skills.
Each problem is structured to challenge different aspects of your knowledge, from basic manipulation to more complex scenarios involving multiple conditions or domain restrictions. By engaging with these examples, you’ll not only strengthen your grasp of fundamental techniques but also build confidence in applying these methods to real-world situations.
Sample Problem 1
Solve for x>:
5x + 3 > 18
Steps:
– Begin by isolating the variable.
– Apply necessary operations to simplify the inequality.
– Ensure the relational symbol is correct after performing any multiplication or division.
Sample Problem 2

Solve for y>:
2(y – 4) ≤ 3y + 5
Steps:
– Distribute and simplify both sides of the equation.
– Combine like terms and isolate the variable.
– Double-check the direction of the relational symbol to ensure accuracy.
Practice is crucial for mastering relational expressions. By consistently working through problems like these, you’ll gain a deeper understanding of the processes involved, helping you tackle more advanced problems with ease.
How to Review Inequalities for Exams
Effective preparation is key to mastering relational problems in mathematics. When preparing for assessments, it’s important to focus on understanding core concepts, practicing problem-solving techniques, and addressing any areas of weakness. A well-structured review process will help you build confidence and improve your ability to tackle a wide range of problems under time pressure.
To make the most of your review time, break down the material into manageable sections, focus on your weak points, and consistently practice various types of problems. This approach will ensure that you not only remember key concepts but also develop the skills to apply them quickly and accurately when it counts.
Step 1: Review Core Concepts

- Ensure that you understand the fundamental principles behind relational expressions.
- Review different types of relational symbols and how to manipulate them.
- Understand how to graph solutions and interpret the results visually.
Step 2: Practice Problem-Solving Techniques
- Work through sample problems and try solving them using various methods.
- Identify common mistakes and learn how to avoid them during the process.
- Time yourself while solving problems to simulate real test conditions.
Consistent practice, combined with a thorough understanding of the material, will enable you to approach any related problem with ease. By reviewing your strengths and addressing areas for improvement, you’ll be well-prepared for any challenge that comes your way.