
Understanding the foundational principles of mathematics is essential for succeeding in higher-level courses. The initial section of the curriculum introduces important topics that lay the groundwork for future learning. Gaining a strong grasp of these concepts will ensure a smoother transition to more advanced subjects and enhance your problem-solving abilities.
To excel in this area, it’s crucial to approach each concept with focus and attention. Familiarity with various methods, from solving equations to interpreting functions, will help build confidence. Regular practice is key, as it allows you to identify patterns and strengthen your ability to apply what you’ve learned.
Through focused practice and the right strategies, you can significantly improve your understanding and performance. Identifying common pitfalls and learning how to avoid them will be essential in mastering the material. With the right approach, you’ll be equipped to tackle any challenge this section presents.
Algebra 2 Chapter 1 Test Overview
This section focuses on the core concepts and skills that are critical for building a solid mathematical foundation. It introduces essential topics that will be explored in greater depth as you progress through the course. Mastery of these initial ideas will provide the tools needed for solving complex problems and understanding advanced techniques.
The material covered emphasizes both theoretical understanding and practical application. Key topics involve manipulating expressions, solving equations, and analyzing mathematical relationships. This foundation is crucial for developing the ability to work with higher-level functions and more intricate problem-solving strategies.
Familiarity with the content and consistent practice will help improve both speed and accuracy. By mastering these concepts, you’ll be well-prepared for more challenging exercises ahead. As you approach this material, it’s important to recognize the interconnections between various mathematical principles and apply them effectively in different contexts.
Key Concepts Covered in Chapter 1
This section introduces a variety of foundational principles that are vital for solving complex mathematical problems. The focus is on understanding core relationships, manipulating expressions, and applying problem-solving techniques. These ideas serve as building blocks for more advanced topics, providing the skills necessary for success in subsequent lessons.
Equations and Expressions
A significant portion of the material involves working with various forms of equations and expressions. Being able to simplify, factor, and solve these mathematical constructs is crucial for progressing through more advanced concepts. Understanding how to manipulate these elements will enable you to tackle a wide range of problems with confidence.
Functions and Graphing
Another key area explored is the relationship between equations and their graphical representations. Knowing how to interpret and graph different types of functions enhances your ability to visualize solutions and make predictions. Mastering this skill is essential for understanding higher-level topics such as transformations and system behavior.
How to Approach Chapter 1 Problems
When tackling problems in this section, it’s important to follow a structured approach. Breaking down complex questions into manageable steps helps prevent confusion and ensures accuracy in your solutions. By understanding the underlying concepts and practicing methodical problem-solving strategies, you’ll improve both your efficiency and confidence.
- Understand the question: Carefully read each problem to ensure you fully understand what is being asked. Identify the key components and what is required in the solution.
- Identify relevant concepts: Determine which principles or techniques apply to the problem at hand. This might involve recognizing the type of equation or the specific method you need to use.
- Break down the problem: If the problem seems complicated, break it down into smaller parts. Solve each piece separately before combining them for the final solution.
- Double-check your work: Once you’ve arrived at an answer, review your calculations to ensure there are no errors. Checking each step can often reveal simple mistakes.
By consistently practicing this approach, you’ll develop a clearer understanding of the material and improve your ability to solve problems efficiently. These steps will also help you stay organized and focused, even when faced with challenging questions.
Common Mistakes to Avoid
When solving mathematical problems, it’s easy to make mistakes, especially when dealing with complex calculations or multiple steps. Recognizing common errors can help prevent them and lead to more accurate results. By understanding where mistakes typically occur, you can develop better problem-solving habits and reduce the likelihood of errors.
One common mistake is failing to properly distribute terms. This often happens when multiplying expressions, leading to incorrect results. Another frequent error is misapplying formulas or rules, especially when working with different types of equations. Be sure to review the conditions and make sure you are using the correct method for each specific problem.
It’s also important to double-check your work for simple calculation errors, such as sign mistakes or arithmetic oversights. Rushing through problems without verifying each step can result in small yet significant errors. Finally, misunderstanding the problem’s requirements, such as missing key information or misinterpreting instructions, can lead to incorrect answers.
Understanding Quadratic Functions
Quadratic functions are one of the most important types of equations in mathematics. They describe parabolic relationships and can be represented in various forms. Understanding how these functions work is crucial for solving problems involving curves, intersections, and motion. By analyzing their structure and behavior, you can unlock key insights into more advanced concepts.
In a quadratic function, the highest degree of the variable is squared, which creates the characteristic parabolic shape when graphed. The equation often takes the form of ax² + bx + c = 0, where the coefficients a, b, and c define the function’s properties, such as its vertex, axis of symmetry, and direction of opening.
| Coefficient | Effect on Graph |
|---|---|
| a | Determines the direction of the parabola (upward if positive, downward if negative) and affects its width. |
| b | Influences the horizontal location of the vertex and the axis of symmetry. |
| c | Shifts the graph vertically and represents the y-intercept. |
By adjusting these values, you can manipulate the shape and position of the parabola. Mastery of quadratic functions allows for effective analysis of real-world situations, from projectile motion to economic modeling.
Mastering Polynomial Operations
Polynomial operations are essential for solving a wide range of mathematical problems. These operations involve manipulating expressions that contain multiple terms, and understanding how to handle them effectively is crucial for advancing in higher-level topics. By mastering these techniques, you will be able to simplify expressions, solve equations, and model real-world scenarios.
Adding and Subtracting Polynomials

When adding or subtracting polynomials, the key is to combine like terms–terms that have the same variable and exponent. This process simplifies the expression and makes it easier to work with. Ensure that you align terms properly and only combine those with the same powers of the variable.
Multiplying Polynomials
Multiplying polynomials requires distributing each term in one polynomial to every term in the other. This distributive property ensures that all possible products are accounted for. Once multiplied, like terms should be combined to simplify the expression further. It’s important to pay close attention to the signs when multiplying, as this can impact the result significantly.
By consistently practicing these operations, you’ll develop a stronger foundation for more complex problems, such as factoring and solving polynomial equations.
Factoring Techniques Explained
Factoring is an essential skill for simplifying expressions and solving equations. It involves breaking down complex terms into simpler components that can be more easily manipulated. Mastering different factoring methods allows for efficient problem-solving and a deeper understanding of mathematical relationships.
Common Factoring Methods
There are several methods used to factor polynomials, depending on the structure of the expression. Understanding when to apply each method is key to simplifying and solving problems quickly.
- Factoring by Grouping: This method is used when an expression has four terms. The terms are grouped in pairs, and common factors are factored out from each group.
- Factoring Trinomials: For expressions with three terms, the goal is to find two numbers that multiply to give the product of the first and last coefficients and add to give the middle term’s coefficient.
- Difference of Squares: This method applies to expressions of the form a² – b². It can be factored as (a – b)(a + b).
- Perfect Square Trinomial: If the expression fits the pattern a² + 2ab + b², it can be factored as (a + b)².
Tips for Efficient Factoring
To factor effectively, always start by checking for a greatest common factor (GCF) that can be factored out. This step simplifies the expression and makes other methods easier to apply. Also, practice recognizing patterns in expressions, as this will allow you to identify the appropriate factoring technique more quickly.
With consistent practice, these factoring techniques become more intuitive and will help you solve complex problems with ease.
Solving Equations with Variables
Solving equations with unknowns involves isolating the variable to find its value. This process requires applying a series of logical steps to simplify the equation and progressively eliminate terms that are not related to the variable. Mastering this skill is crucial for solving a wide variety of problems, both in mathematics and real-life applications.
One of the first steps in solving an equation is to simplify both sides as much as possible. This includes combining like terms and using basic operations such as addition, subtraction, multiplication, or division. Once the equation is simplified, the goal is to isolate the variable by performing inverse operations to both sides of the equation.
For example, to solve for x in an equation like 2x + 5 = 15, you would first subtract 5 from both sides, resulting in 2x = 10. Then, divide both sides by 2 to get the solution x = 5.
It’s also important to be aware of potential pitfalls, such as distributing terms incorrectly or making mistakes with signs. Consistent practice will improve your accuracy and speed in solving equations.
Graphing and Interpreting Functions
Graphing functions involves plotting points on a coordinate plane to visualize the relationship between variables. Interpreting these graphs provides valuable insights into how the variables interact and change in response to each other. This process is essential for understanding patterns, trends, and behaviors in various mathematical and real-world scenarios.
To graph a function, start by selecting a range of values for the independent variable, then calculate the corresponding values for the dependent variable. Plot these pairs of points on the graph and connect them smoothly to reveal the function’s shape. Different types of functions produce distinct graphs, such as straight lines, curves, or parabolas.
Interpreting the graph involves analyzing key features, such as the slope, intercepts, and overall behavior of the function. The slope indicates the rate of change, while the intercepts show where the graph crosses the axes. By examining these elements, you can gain a deeper understanding of the function’s properties and its implications in a given context.
Working with Rational Expressions
Rational expressions involve ratios of two polynomials, and manipulating these expressions requires understanding how to simplify, add, subtract, multiply, and divide them effectively. Mastering these operations is essential for solving complex mathematical problems, especially those that involve fractions or proportional relationships. The goal is to work with these expressions in a way that simplifies the problem and makes it easier to find a solution.
Simplifying Rational Expressions
Simplifying a rational expression involves factoring both the numerator and denominator and canceling out any common factors. The process is similar to simplifying fractions, but with polynomials. It is important to check that the expression does not have any factors that would make the denominator equal to zero, as this would result in an undefined expression.
- Factor both the numerator and denominator.
- Cancel out common factors in both parts.
- Ensure the denominator does not equal zero after simplifying.
Operations with Rational Expressions
Performing operations such as addition, subtraction, multiplication, and division with rational expressions follows similar rules to those used for fractions. However, additional steps may be required, such as finding a common denominator when adding or subtracting, or factoring expressions when multiplying or dividing.
- Addition/Subtraction: Find a common denominator before combining terms.
- Multiplication: Multiply the numerators and denominators directly, then simplify.
- Division: Multiply by the reciprocal of the second expression.
By practicing these steps and familiarizing yourself with the rules, you will be able to handle rational expressions with greater ease and accuracy.
Linear Systems and Their Solutions
Linear systems involve multiple equations with the same set of variables. The goal is to find the values of the variables that satisfy all equations in the system simultaneously. Solving these systems provides insights into how different conditions or constraints interact with each other in mathematical models.
There are several methods for solving systems of linear equations, including substitution, elimination, and graphing. Each method has its advantages depending on the nature of the system and the form of the equations. Mastering these methods enables efficient problem-solving and a deeper understanding of relationships between variables.
Methods for Solving Linear Systems
When solving linear systems, the most common approaches are substitution and elimination. Each method aims to reduce the system to a simpler form, making it easier to identify the solution.
- Substitution Method: This method involves solving one equation for one variable and then substituting that expression into the other equation(s).
- Elimination Method: By adding or subtracting equations, this method eliminates one variable, allowing the other to be easily solved.
- Graphing Method: This approach involves plotting both equations on a graph and finding the point where the lines intersect, which represents the solution to the system.
Solution Types
The solution to a linear system can fall into one of three categories: one solution, no solution, or infinitely many solutions. Understanding how to interpret the results of each method is key to identifying the correct type of solution.
| Solution Type | Interpretation |
|---|---|
| One Solution | The lines intersect at a single point, indicating a unique solution. |
| No Solution | The lines are parallel and do not intersect, indicating that no solution exists. |
| Infinitely Many Solutions | The lines are coincident, meaning they overlap entirely and have an infinite number of intersection points. |
By applying these methods and analyzing the results, you can solve systems of equations and uncover valuable information about the relationships between different variables.
Using the Distributive Property
The distributive property is a powerful tool in simplifying expressions and solving equations. It allows you to multiply a number or term across a sum or difference within parentheses, making complex expressions easier to work with. By applying this property, you can break down problems into simpler components and streamline your calculations.
To apply the distributive property, you multiply each term inside the parentheses by the term outside. This helps eliminate parentheses and combine like terms, making it easier to solve equations or simplify expressions. It’s a foundational concept that is used extensively in many areas of mathematics.
Example of the Distributive Property
Consider the expression 3(x + 4). By distributing the 3 to both terms inside the parentheses, the expression becomes:
- 3(x + 4) = 3x + 12
This shows how multiplying a term by a sum results in multiplying the term by each individual term within the parentheses.
Applications of the Distributive Property
The distributive property is useful in many areas, including simplifying complex algebraic expressions, solving linear equations, and factoring polynomials. Whether you’re dealing with variables or constants, this property helps to break down problems into manageable steps. Additionally, it is crucial in simplifying expressions that involve both addition and multiplication.
By mastering the distributive property, you will have a versatile tool that makes it easier to manipulate and solve a variety of mathematical problems.
Tips for Efficient Preparation
Effective preparation is the key to performing well when tackling any set of problems. By focusing on the right strategies, you can maximize your understanding and ensure you’re fully ready for the challenge. Approaching the material in a structured manner will help you retain key concepts and apply them when needed.
Start by organizing your study time. Identify which areas require the most attention and prioritize them. Practice regularly to reinforce your understanding and build confidence. Don’t just memorize formulas–aim to understand the underlying principles so that you can apply them in various scenarios.
Focus on Key Concepts

While reviewing, pay special attention to fundamental ideas and techniques that are commonly tested. Revisit the most challenging topics and spend extra time on those. Breaking down complex concepts into smaller parts can make them more manageable and less overwhelming.
- Revisit core principles: Make sure you understand the basic rules and formulas used in problem-solving.
- Practice different types of problems: The more diverse your practice, the better prepared you’ll be for unexpected challenges.
- Review mistakes: Go over any mistakes from previous exercises to understand what went wrong and how to correct it.
Utilize Practice Materials
Working through sample problems, quizzes, and past exercises helps solidify your grasp on various topics. Set aside time each day to practice, using a mix of easy, intermediate, and difficult problems. This approach will build both your problem-solving skills and speed.
Lastly, try to simulate the testing environment. Time yourself while practicing problems to ensure you’re able to work efficiently under pressure. This helps you manage your time effectively when faced with real challenges.
Practice Problems for Chapter 1
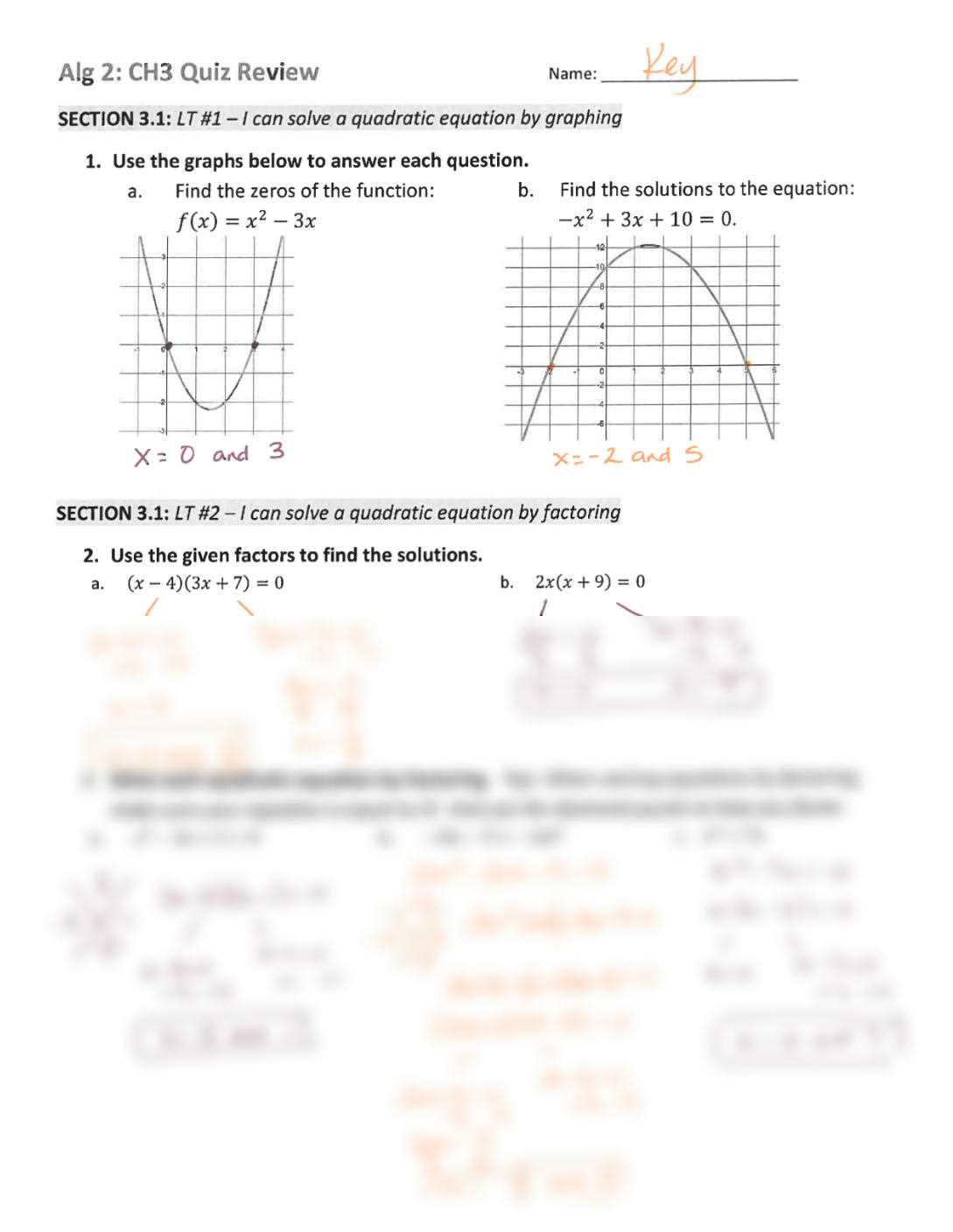
Practicing a variety of problems is one of the most effective ways to reinforce your understanding of key concepts. By solving different types of exercises, you can familiarize yourself with the material and develop the skills needed to solve similar questions in a more efficient manner. This section provides several problems that will help you test your knowledge and improve your problem-solving ability.
Example Problems
Below are a few practice problems that cover the essential topics discussed. Try to solve them on your own, and check the solutions afterward to ensure you understand the reasoning behind each answer.
| Problem | Solution |
|---|---|
| 1. Simplify: 4(x + 5) – 3x | Solution: 4x + 20 – 3x = x + 20 |
| 2. Solve for x: 2x – 5 = 13 | Solution: 2x = 18, x = 9 |
| 3. Factor: x² + 5x + 6 | Solution: (x + 2)(x + 3) |
| 4. Solve: 3(x – 4) = 2x + 5 | Solution: x = 17 |
Advanced Practice
For more advanced practice, consider attempting problems that involve multiple steps or more complex operations. These problems will help you apply the concepts you’ve learned to more challenging scenarios.
- Solve for x: 5(x + 2) = 3x + 20
- Simplify: (2x + 3)(x – 1)
- Factor: x² – 4x – 21
As you work through these problems, be sure to check your solutions and ensure you are applying the correct methods. The more practice you get, the more confident you will become in your ability to tackle similar problems during assessments.
How to Check Your Answers
Ensuring that your solutions are correct is a crucial step in mastering any mathematical concept. After completing a problem, it’s essential to verify that you’ve followed the right steps and arrived at the correct result. Below are some effective methods to check your work and confirm that your solutions are accurate.
Methods for Verification
- Substitute the solution back into the original equation: One of the most straightforward ways to check your solution is to substitute it back into the original expression. If both sides of the equation are equal, then your answer is correct.
- Check the units and context: In word problems or applied mathematics, ensure that your solution makes sense in the context. Verify that your units are consistent and that the result is reasonable.
- Revisit each step: Review each step of your solution carefully. Check for errors such as sign mistakes, misapplied rules, or missed steps in the process.
- Use alternative methods: If possible, solve the problem using a different approach or technique. If both methods lead to the same result, it provides additional confidence that your solution is correct.
Additional Tips for Effective Checking
- Break down complex problems: If the problem is complex, break it into smaller, manageable parts. This makes it easier to check each part individually.
- Double-check your calculations: If you’ve performed calculations, such as adding, subtracting, multiplying, or dividing, go over them once again to make sure they are accurate.
- Work backward: In some cases, working backward from the solution can help verify the steps you took to arrive at it.
By using these strategies, you’ll be able to catch common mistakes and increase your confidence in your solutions. Consistent practice with checking your work will make this process faster and more intuitive over time.
Strategies for Time Management
Efficient time management is essential when preparing for any type of academic assessment. Balancing practice, review, and rest ensures that you are well-prepared without feeling overwhelmed. Implementing effective strategies can help you stay organized, maximize your study sessions, and reduce stress as you approach your goals.
Effective Time Management Techniques
- Set clear, achievable goals: Break your preparation into smaller, specific tasks. Setting achievable goals ensures that you stay focused and can track your progress efficiently.
- Create a study schedule: Allocate fixed time slots for each topic. A structured schedule allows you to distribute your efforts evenly across all areas, avoiding last-minute cramming.
- Prioritize tasks: Start with the most challenging or unfamiliar topics and work your way to easier ones. This ensures that you tackle difficult material while your mind is fresh.
- Use active learning techniques: Incorporate active learning methods such as practice problems, summarizing key points, and self-quizzing to engage with the material more effectively.
Maintaining Focus and Efficiency
- Limit distractions: Create a study environment free of distractions. Turn off notifications, put away your phone, and find a quiet space to work.
- Take regular breaks: Avoid burnout by following the Pomodoro Technique–study for 25 minutes and take a 5-minute break. This method helps maintain focus and prevents fatigue.
- Review regularly: Instead of cramming all at once, review material periodically. This helps reinforce your understanding and retains information longer.
Sample Time Management Table
| Time Slot | Activity |
|---|---|
| 9:00 AM – 10:00 AM | Review key concepts and formulas |
| 10:00 AM – 10:30 AM | Practice problems (focus on weaknesses) |
| 10:30 AM – 11:00 AM | Take a break, stretch, hydrate |
| 11:00 AM – 12:00 PM | Complete practice exercises |
| 12:00 PM – 1:00 PM | Lunch break and relaxation |
| 1:00 PM – 2:00 PM | Review mistakes from practice exercises |
By adhering to these strategies, you can manage your preparation time effectively, reducing stress and increasing your chances of success. Consistency in planning and following through is key to maximizing your productivity and achieving your goals with confidence.
Reviewing Common Algebraic Formulas
Familiarizing yourself with essential mathematical expressions is crucial for solving problems efficiently. These formulas serve as the foundation for many operations, providing shortcuts to complex calculations. Whether working with polynomials, quadratics, or equations involving variables, knowing the key formulas will streamline your approach and improve accuracy.
Essential Mathematical Formulas
- Quadratic Formula: Used to solve second-degree equations of the form ax2 + bx + c = 0. The solution is given by:
- x = (-b ± √(b² – 4ac)) / 2a
- Distributive Property: For multiplying a number across an addition or subtraction expression, the formula is:
- a(b + c) = ab + ac
- Sum of Squares: Used when adding two squared terms. The formula is:
- a² + b² = (a + b)(a – b)
- Factoring Quadratics: The general factoring formula for quadratics is:
- ax2 + bx + c = (px + q)(rx + s)
Important Tips for Using Formulas
- Understand the Structure: Ensure you identify the correct components of each equation before applying a formula.
- Use Factorization When Possible: Factorizing expressions can simplify equations and reduce the need for complex calculations.
- Keep a Formula Sheet Handy: Write down key formulas for quick reference during practice or problem-solving sessions.
By mastering these fundamental expressions, you’ll be able to tackle a variety of problems with confidence and efficiency. Regular practice will ensure that these formulas become second nature, aiding in both speed and accuracy when solving mathematical challenges.
Next Steps After Chapter 1

Once you’ve mastered the foundational concepts and skills introduced in the first section, it’s essential to continue building on that knowledge. Moving forward, you should aim to deepen your understanding by tackling more complex topics and honing your problem-solving techniques. The next steps will focus on reinforcing what you’ve learned while introducing new challenges to expand your skills.
Consolidate Your Understanding
- Review Key Concepts: Go over the main principles you’ve encountered so far. Make sure you fully grasp the foundational ideas, as they will be essential in future sections.
- Practice More Problems: The more problems you solve, the better you’ll become at applying the concepts to different scenarios. Consider working through additional practice exercises or worksheets.
- Seek Clarification: If any concepts are unclear, take time to revisit them. You may want to ask questions or seek additional resources, such as online tutorials or study groups.
Explore New Topics
- Progress to Advanced Techniques: Start tackling more advanced operations, such as solving more complex equations, working with functions, and understanding graphing techniques.
- Understand Real-World Applications: Look at how the concepts you’ve learned apply to real-world situations, whether in finance, engineering, or other fields.
- Challenge Yourself: Don’t shy away from problems that push your limits. Practicing harder questions will help you improve and prepare for more difficult material.
By moving forward with these steps, you’ll ensure that your understanding grows steadily and that you are well-prepared for the upcoming material. The key is consistent practice and continued learning to solidify your knowledge and skills.