
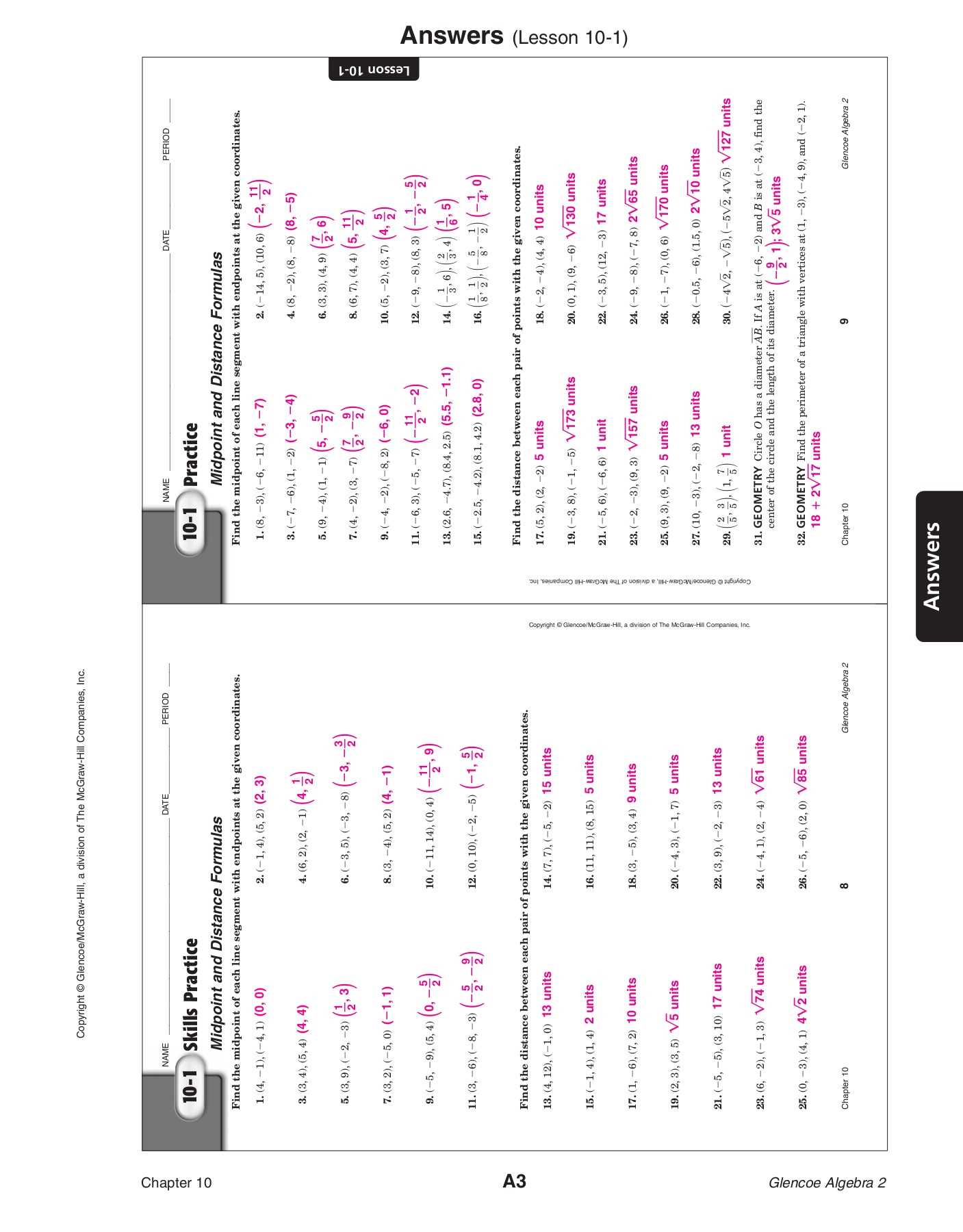
In this section, we will explore essential methods and approaches to solving complex mathematical challenges. These techniques are designed to help you strengthen your problem-solving abilities and gain a deeper understanding of higher-level math concepts.
By breaking down intricate problems into manageable steps, you will build the confidence needed to tackle even the most difficult exercises. This process will guide you through important calculations, simplifying them in ways that make the learning process both effective and rewarding.
Strengthening your foundation in these methods will be crucial for mastering advanced topics, and applying them correctly will significantly improve your mathematical proficiency. With consistent practice, these strategies will become second nature, allowing you to approach any problem with ease.
Skills Practice Answers for Algebra 2
To excel in advanced mathematics, it’s crucial to apply a structured approach to solving problems. Each step, when performed accurately, contributes to a deeper understanding of complex topics and prepares you for more challenging tasks. Whether you’re solving equations or graphing functions, the key to mastering these concepts lies in consistent practice and applying learned strategies effectively.
Breaking Down Complex Problems

When faced with difficult exercises, breaking them into smaller parts allows for easier comprehension. Here’s how to tackle complex problems:
- Identify the type of problem you are dealing with.
- Analyze the given information and separate the known values.
- Apply the appropriate formulas or methods to simplify the expression.
- Double-check the calculations for accuracy.
- Interpret the results and re-evaluate if necessary.
Common Strategies for Problem Solving
Utilizing various strategies will not only improve your speed but also the quality of your solutions. Some of these include:
- Factoring to simplify expressions.
- Substitution for solving systems of equations.
- Graphing to visualize relationships between variables.
- Using the quadratic formula for solving second-degree equations.
- Working with inequalities to understand constraints and boundaries.
By mastering these techniques and regularly applying them to exercises, you will significantly enhance your problem-solving skills and gain a more solid grasp of the subject matter.
Understanding Key Concepts in Algebra 2
Grasping the core principles of advanced mathematics is essential for solving more intricate equations and functions. A clear understanding of these fundamental ideas serves as the foundation for tackling more challenging topics. The ability to break down complex problems into simpler components allows for more effective solutions and greater retention of knowledge.
Fundamental Topics to Master
There are several essential topics that form the basis of advanced mathematical study. These concepts are often used repeatedly and must be well understood to succeed in this area:
| Concept | Definition | Applications |
|---|---|---|
| Equations | A mathematical statement with an equal sign, indicating that two expressions are equal. | Solving for unknown values, simplifying expressions, and modeling real-world problems. |
| Functions | A relationship between two sets of values where each input has a unique output. | Graphing relationships, analyzing rates of change, and modeling trends. |
| Polynomials | Expressions consisting of variables raised to powers and multiplied by coefficients. | Solving polynomial equations, factoring, and graphing curves. |
| Rational Expressions | Fractions involving polynomials in both the numerator and the denominator. | Simplifying expressions, solving rational equations, and analyzing asymptotes. |
Applying Concepts to Real-Life Problems
Understanding these concepts not only helps in theoretical exercises but also enables practical applications. Real-world scenarios such as financial planning, engineering, and even data analysis require a strong command of these topics. By applying the techniques learned, one can model various situations and find solutions with precision and confidence.
Step-by-Step Solutions for Practice Problems
To fully understand and solve mathematical problems, it’s important to break them down into manageable steps. This method not only helps in finding the correct solution but also ensures that each part of the problem is understood thoroughly. By following a clear process, solving complex equations becomes more straightforward and less intimidating.
Breaking Down the Problem
The first step in solving any exercise is to carefully analyze the problem and identify key components. Each type of equation or function requires a slightly different approach, but following a structured method makes the process much easier:
| Step | Action | Explanation |
|---|---|---|
| 1 | Identify the variables | Determine which quantities need to be solved for and what is already known. |
| 2 | Set up the equation | Write the equation based on the given information, ensuring all terms are correctly represented. |
| 3 | Simplify the equation | Combine like terms, factor if necessary, and simplify both sides to make solving easier. |
| 4 | Solve for the unknowns | Use appropriate methods like substitution, elimination, or factoring to solve for the variable(s). |
| 5 | Verify the solution | Check the solution by substituting it back into the original equation to confirm it satisfies all conditions. |
Common Techniques for Solving Problems
There are several approaches that can be used depending on the nature of the problem. Mastering these methods will greatly improve your ability to solve a wide range of exercises:
- Substitution: Replacing a variable with its value from another equation.
- Elimination: Removing one variable by adding or subtracting equations.
- Factoring: Breaking down complex expressions into simpler factors to solve equations.
- Graphing: Plotting equations on a coordinate plane to find the solution visually.
- Using the quadratic formula: Solving quadratic equations directly with a formula when factoring is difficult.
By practicing these techniques and following each step methodically, you will become more adept at solving mathematical problems with confidence and accuracy.
Mastering Equations and Inequalities
Successfully solving equations and inequalities is a fundamental aspect of advanced mathematics. Whether dealing with linear, quadratic, or higher-degree expressions, the ability to manipulate and solve these problems is essential for tackling more complex challenges. Understanding the principles behind these mathematical tools allows for greater flexibility and precision in problem-solving.
Equations represent relationships between quantities, while inequalities express limitations or constraints. Both require a clear approach and a solid grasp of mathematical rules to achieve the correct solution. By mastering techniques such as balancing, isolating variables, and applying specific properties, one can confidently approach various types of equations and inequalities.
With consistent practice and a methodical approach, mastering these concepts will enable you to solve problems more efficiently and build a strong foundation for further mathematical learning.
Solving Quadratic Equations Effectively
Quadratic equations are a crucial aspect of advanced mathematics, and mastering the methods to solve them is essential for further study. These equations typically involve variables raised to the second power and can be solved in several ways, each suitable for different types of problems. A solid understanding of the techniques involved will allow you to approach and solve them efficiently.
The most common methods for solving these equations include factoring, completing the square, and using the quadratic formula. Each approach has its own strengths, and knowing when to apply each one is key to simplifying the process and arriving at the correct solutions. By practicing these methods and understanding their underlying principles, solving quadratics becomes a straightforward task.
With the right strategy, quadratic equations can be tackled with confidence and ease, providing a strong foundation for tackling more complex mathematical challenges.
Exploring Rational Expressions and Functions

Rational expressions and functions are powerful tools in mathematics, often used to model real-world scenarios and solve complex problems. These expressions involve ratios of polynomials and can be simplified, multiplied, divided, or combined to solve a variety of equations. Understanding how to manipulate these functions is essential for tackling more advanced topics.
Key Concepts to Understand
To effectively work with rational expressions, it’s important to understand a few fundamental concepts:
- Domain: The set of values for which the function is defined. Typically, values that make the denominator equal to zero are excluded.
- Simplification: Reducing the expression to its simplest form by factoring the numerator and denominator and canceling out common factors.
- Multiplication and Division: Multiplying or dividing rational expressions requires multiplying numerators with numerators and denominators with denominators, simplifying afterward.
- Addition and Subtraction: To add or subtract rational functions, a common denominator must first be found, after which the numerators can be combined.
Steps to Solve Rational Functions
When working with rational expressions, following a structured approach ensures accuracy and efficiency:
- Identify the domain of the expression to avoid division by zero.
- Simplify the expression by factoring the numerator and denominator where possible.
- Perform operations like multiplication, division, addition, or subtraction according to the problem.
- Check for any possible simplifications after the operation, and verify the final expression.
By practicing these methods and becoming familiar with the different types of rational expressions, you will gain confidence in solving more complex problems and applying these functions to real-world situations.
Working with Exponents and Radicals
Exponents and radicals are essential concepts in mathematics, frequently used to express large numbers in a more compact form or to represent roots of values. Mastering these operations allows for efficient problem-solving and a deeper understanding of various mathematical relationships. Whether simplifying expressions or solving complex equations, these concepts are fundamental for success in higher-level mathematics.
Understanding Exponent Rules
Exponents describe repeated multiplication of a base number. There are several important rules that help simplify expressions involving exponents:
- Product of Powers: When multiplying numbers with the same base, add the exponents. For example, am × an = am+n.
- Quotient of Powers: When dividing numbers with the same base, subtract the exponents. For example, am ÷ an = am-n.
- Power of a Power: When raising a power to another power, multiply the exponents. For example, (am)n = am×n.
- Negative Exponents: A negative exponent means to take the reciprocal of the base. For example, a-n = 1/an.
- Zero Exponent: Any nonzero number raised to the power of zero equals one. For example, a0 = 1.
Working with Radicals
Radicals involve roots, such as square roots or cube roots, which represent the inverse operation of raising a number to a power. Here are some key points to keep in mind:
- Square Root: The square root of a number x is a number that, when multiplied by itself, gives x. It is denoted as √x.
- Cube Root: The cube root of a number x is a number that, when multiplied by itself three times, gives x. It is denoted as ³√x.
- Rationalizing the Denominator: When a radical appears in the denominator, it is often simplified by multiplying the numerator and denominator by the appropriate radical to eliminate the radical in the denominator.
- Combining Radicals: Similar to exponents, when combining radicals with the same index, the radicands (the numbers under the radical sign) can be multiplied or divided.
By applying these rules and understanding the relationship between exponents and radicals, you will be better equipped to handle a variety of mathematical problems that involve these concepts.
Graphing Linear and Nonlinear Functions
Graphing functions is a key skill in mathematics, as it allows you to visually represent relationships between variables. Understanding how to graph both linear and nonlinear equations helps in analyzing data, solving problems, and identifying trends. Whether dealing with straight lines or curves, knowing the steps to plot these functions will enhance your ability to interpret and work with mathematical expressions.
Linear functions are characterized by constant rates of change and result in straight-line graphs. These are relatively simple to graph, as they follow a predictable pattern. On the other hand, nonlinear functions can involve curves, exponential growth, or other complex shapes, making their graphs more intricate. Being able to identify the nature of a function will help determine the most efficient method for graphing.
By mastering the techniques for graphing both types of functions, you can gain a deeper understanding of their behavior and apply this knowledge to solve a wide range of problems in mathematics and real-world applications.
Factoring Techniques in Algebra 2
Factoring is an essential skill in advanced mathematics that involves breaking down complex expressions into simpler components. By mastering various factoring methods, you can solve equations more efficiently and simplify complex problems. Recognizing the right technique for a given expression allows you to unlock solutions that might otherwise seem challenging.
Several methods are used for factoring, each applicable to different types of expressions. Here are some of the most common techniques:
- Greatest Common Factor (GCF): Identify the largest factor shared by all terms in the expression, then factor it out.
- Factoring by Grouping: When an expression has four terms, group terms in pairs, factor each pair, and then factor out the common binomial.
- Difference of Squares: This technique applies when an expression is the difference between two squared terms. The factored form is a² – b² = (a – b)(a + b).
- Trinomial Factoring: Used for expressions in the form ax² + bx + c, where you find two numbers that multiply to give ac and add to give b.
- Perfect Square Trinomial: Recognize and factor trinomials that are perfect squares, such as a² + 2ab + b² = (a + b)².
By applying these techniques, you can simplify complex expressions and solve problems more efficiently. As you practice, you will become more adept at identifying the best factoring method for any given problem, making advanced mathematical tasks much more manageable.
Solving Systems of Equations and Inequalities

Solving systems of equations and inequalities is a fundamental skill in mathematics, allowing you to find the values that satisfy multiple conditions simultaneously. This concept is widely used in fields such as physics, economics, and engineering, where multiple relationships must be considered at once. By learning how to solve these systems, you can analyze complex situations and make informed decisions based on the given constraints.
When solving systems of equations, the goal is to find the point or points where the equations intersect. These solutions represent values that satisfy all equations in the system. On the other hand, solving systems of inequalities involves finding the region where all the inequalities overlap, often represented graphically as a shaded area. The method you choose to solve these systems depends on the type of equations or inequalities involved and the tools available.
Understanding different methods for solving these systems, including substitution, elimination, and graphical techniques, will help you approach problems with confidence and accuracy.
Polynomials and Their Applications in Algebra
Polynomials are mathematical expressions that consist of variables raised to whole-number powers, combined with coefficients. These expressions are a key part of many mathematical problems and can represent a wide variety of relationships in real-world situations. Understanding how to work with polynomials is essential for solving equations, modeling physical systems, and analyzing data.
In many cases, polynomials are used to model growth patterns, optimize processes, or describe complex phenomena. For instance, quadratic expressions are often used in projectile motion, while cubic and higher-degree polynomials can model more intricate systems like population dynamics or the behavior of materials under stress.
Basic Operations with Polynomials
Working with polynomials involves several key operations:
- Addition and Subtraction: Combine like terms by adding or subtracting their coefficients.
- Multiplication: Multiply each term in one polynomial by every term in the other polynomial.
- Division: Polynomial long division or synthetic division can be used to divide one polynomial by another.
Applications of Polynomials in Problem Solving
Polynomials can also be used to solve problems across various disciplines. They allow for efficient modeling of economic growth, population shifts, and other real-world processes. By finding the roots of a polynomial, one can identify key points such as maximum and minimum values or points of intersection in graphical representations.
Mastering polynomial operations and their applications will enhance your ability to tackle complex problems and apply mathematical techniques to a wide range of fields.
Learning About Logarithmic and Exponential Functions
Logarithmic and exponential functions are two of the most important mathematical concepts used to model a variety of real-world situations. These functions are closely related and serve as the foundation for understanding growth and decay processes, such as population dynamics, radioactive decay, and financial interest calculations. Mastering these functions is essential for analyzing how quantities change over time or in response to varying conditions.
Exponential functions describe processes where quantities increase or decrease at a constant rate, such as compound interest or population growth. These functions have the form y = a * b^x, where a is the initial amount, b is the base, and x is the exponent. In contrast, logarithmic functions are the inverse of exponential functions. They allow us to solve equations where the unknown appears as the exponent. The general form of a logarithmic function is y = log_b(x), where b is the base and x is the argument.
Applications of Exponential and Logarithmic Functions

These functions have broad applications in fields such as science, finance, and engineering:
- Population Growth: Exponential functions are often used to model the growth of populations over time, where the growth rate is constant.
- Radioactive Decay: Exponential decay functions describe the reduction in the amount of a substance over time, such as the decay of radioactive materials.
- Finance: Compound interest calculations use exponential functions to determine the growth of investments over time.
- Sound Intensity: Logarithmic functions are used to measure the intensity of sound, such as in decibels.
Solving Equations Involving Exponents and Logarithms
Solving equations involving exponential and logarithmic functions requires a good understanding of their properties. Techniques such as logarithmic properties, change of base formula, and exponent rules allow you to simplify and solve complex equations effectively. For example, you can solve for x in exponential equations by taking the logarithm of both sides, or you can solve logarithmic equations by exponentiating both sides to eliminate the logarithm.
With practice and a clear understanding of these concepts, you will be able to confidently solve problems involving exponential and logarithmic functions, making them powerful tools for problem-solving and real-world applications.
Understanding Arithmetic and Geometric Sequences
Sequences are ordered lists of numbers that follow a specific pattern. Two of the most fundamental types of sequences in mathematics are arithmetic and geometric sequences. Each type has its own unique structure, and understanding how they work is crucial for solving problems in many areas, including finance, physics, and computer science.
An arithmetic sequence is characterized by a constant difference between consecutive terms. This regularity makes arithmetic sequences useful for modeling situations where the change between each step is the same. On the other hand, geometric sequences involve a constant ratio between successive terms, which allows them to model exponential growth or decay, such as population increases or the depreciation of assets.
Key Features of Arithmetic Sequences
In an arithmetic sequence, the difference between each consecutive term is always the same, referred to as the common difference. The general form of an arithmetic sequence is:
- First Term (a): The initial value of the sequence.
- Common Difference (d): The fixed amount added or subtracted to each term to get the next one.
- General Formula: an = a + (n – 1) * d, where an is the nth term, a is the first term, and d is the common difference.
Understanding Geometric Sequences
In a geometric sequence, each term is found by multiplying the previous term by a constant called the common ratio. This ratio determines how fast the sequence grows or decays. Geometric sequences are commonly used to model exponential growth or decay, such as the growth of money in a compound interest account or the decrease in the amount of a substance over time.
- First Term (a): The starting point of the sequence.
- Common Ratio (r): The constant factor by which each term is multiplied to get the next term.
- General Formula: an = a * r^(n – 1), where an is the nth term, a is the first term, and r is the common ratio.
Understanding these sequences will help you solve various real-life problems involving growth, change, and patterns. By mastering the methods for working with both arithmetic and geometric sequences, you will be better equipped to tackle complex problems that involve constant change and proportional relationships.
Applying Functions in Real-Life Problems
Mathematical functions are not just abstract concepts; they have practical applications that can help us solve real-world challenges. By understanding how different types of functions work, we can model various phenomena such as growth, decay, and motion. These models are widely used in fields such as economics, engineering, biology, and physics, making functions essential tools for decision-making and problem-solving.
For instance, linear functions can be used to model situations where there is a constant rate of change, such as calculating expenses or predicting future earnings. Quadratic functions, on the other hand, are useful for situations involving areas, projectile motion, or optimizing profits. Exponential functions help model rapid growth or decay, such as in population studies or radioactive decay.
Common Applications of Functions
Functions can be applied in a variety of ways, and understanding their forms is essential for solving real-life problems. Some common examples include:
- Linear Functions: These are used in budgeting, sales projections, and determining speed or distance traveled over time.
- Quadratic Functions: Used in calculating the area of a circle or optimizing solutions for profit maximization in business.
- Exponential Functions: Applied to model population growth, radioactive decay, or compound interest calculations.
- Logarithmic Functions: Help analyze the growth rates and measure the intensity of sound or light in scientific experiments.
Example: Using Functions to Predict Growth
Imagine a scenario where a company is launching a new product. By using exponential functions, they can estimate how their customer base might grow over time. The growth rate could be modeled using a function that tracks how the customer base increases as more people buy the product each month. By understanding the function, the company can predict sales, manage inventory, and plan marketing strategies.
In another example, engineers can use quadratic functions to design and test the optimal shape for a bridge or an arch, where the function helps determine the structure’s maximum strength or efficiency. By applying these functions, engineers can create safer and more cost-effective designs.
Mastering the application of functions in real-life situations equips individuals with powerful tools to solve a wide array of practical problems. From financial forecasting to scientific research, understanding the role of functions is key to making informed decisions and achieving successful outcomes.
Common Mistakes to Avoid in Algebra 2
Mathematical challenges often arise due to small errors that can have a big impact on the outcome of a problem. Many students encounter similar issues when working through complex equations, functions, and systems. Recognizing and avoiding these common mistakes can greatly improve understanding and lead to more accurate solutions. By focusing on key concepts and strategies, learners can navigate through common pitfalls and strengthen their problem-solving skills.
Some of the most frequent mistakes include misapplying rules, overlooking negative signs, and confusing different types of equations. Understanding the specific areas where errors are likely to occur allows students to approach each problem with a more careful and methodical mindset.
1. Confusing Operations with Exponents
One common mistake is mishandling operations involving exponents. Students sometimes forget to apply the correct order of operations, especially when exponents are present along with addition or subtraction. For example, in an expression like 2 + 3², many may mistakenly add 2 and 3 first before squaring, resulting in an incorrect answer.
- Always follow the order of operations: Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right).
- Remember that exponents indicate repeated multiplication, not addition or subtraction.
2. Ignoring Negative Signs
Another common issue occurs when students forget to account for negative signs, particularly when dealing with equations or expressions involving subtraction or factoring. Missing a negative sign can lead to a completely incorrect result. For example, -3(4x + 2) should be correctly expanded as -12x – 6, not 12x + 6.
- Always double-check signs, especially when distributing or simplifying expressions.
- Ensure that negative signs are properly accounted for when performing operations on negative numbers.
3. Incorrect Factoring
Factoring is an essential skill, but it’s easy to make mistakes when trying to break down expressions. A common error is incorrectly factoring quadratic equations or polynomials. For example, in the expression x² + 5x + 6, the correct factorization is (x + 2)(x + 3), but it’s easy to make mistakes when pairing terms incorrectly.
- Use methods like trial and error, the FOIL method, or the quadratic formula carefully to check your work.
- Verify the factorization by multiplying the terms back out to ensure accuracy.
Being aware of these common mistakes and taking steps to avoid them will improve your performance and help you tackle more advanced concepts with confidence. Through consistent practice and careful attention to detail, these errors can be minimized, leading to a deeper understanding of mathematical principles.
Tips for Improving Algebra 2 Skills
Mastering advanced mathematical concepts requires dedication, practice, and an organized approach. As students tackle more complex equations and functions, it’s important to focus on developing a deep understanding of the material. By honing problem-solving strategies and learning how to apply key techniques, you can enhance your ability to navigate challenges with greater ease.
Here are several effective strategies to strengthen your mathematical abilities and build confidence when approaching difficult topics.
1. Break Down Complex Problems

When faced with complicated equations or systems, it’s easy to become overwhelmed. Instead of trying to solve everything in one go, break the problem down into smaller, more manageable steps. Identify the key components and work through them one at a time. This approach not only makes the problem less daunting but also helps ensure that each part is solved correctly.
- Start by identifying what is being asked and what information is already provided.
- Divide the problem into smaller sections, solving each step individually.
- Double-check your work as you go to ensure accuracy at each stage.
2. Master Core Concepts Before Moving On
It’s crucial to have a solid understanding of foundational concepts before moving on to more advanced topics. Struggling with basic principles can lead to confusion as more complex material is introduced. Take the time to fully understand each concept and ensure that you can apply it in different scenarios. Whether it’s solving linear equations or working with polynomials, mastering the basics will provide a strong base for tackling more difficult problems later on.
- Review key concepts regularly to reinforce your understanding.
- Work through example problems to gain confidence with each new technique.
- If you find a topic particularly challenging, don’t hesitate to revisit earlier material for clarification.
By applying these strategies, you can develop a more systematic approach to solving mathematical problems and improve your overall proficiency. As you gain experience and confidence, you’ll find that complex tasks become more manageable and less intimidating.