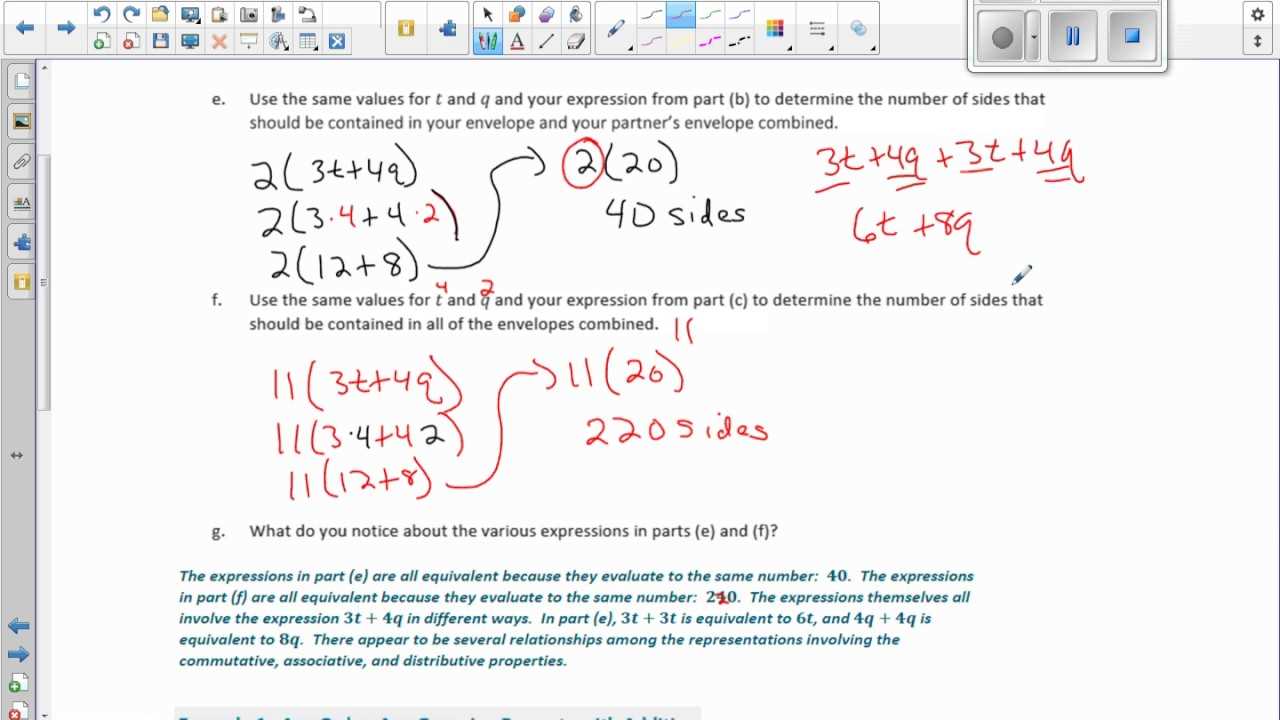
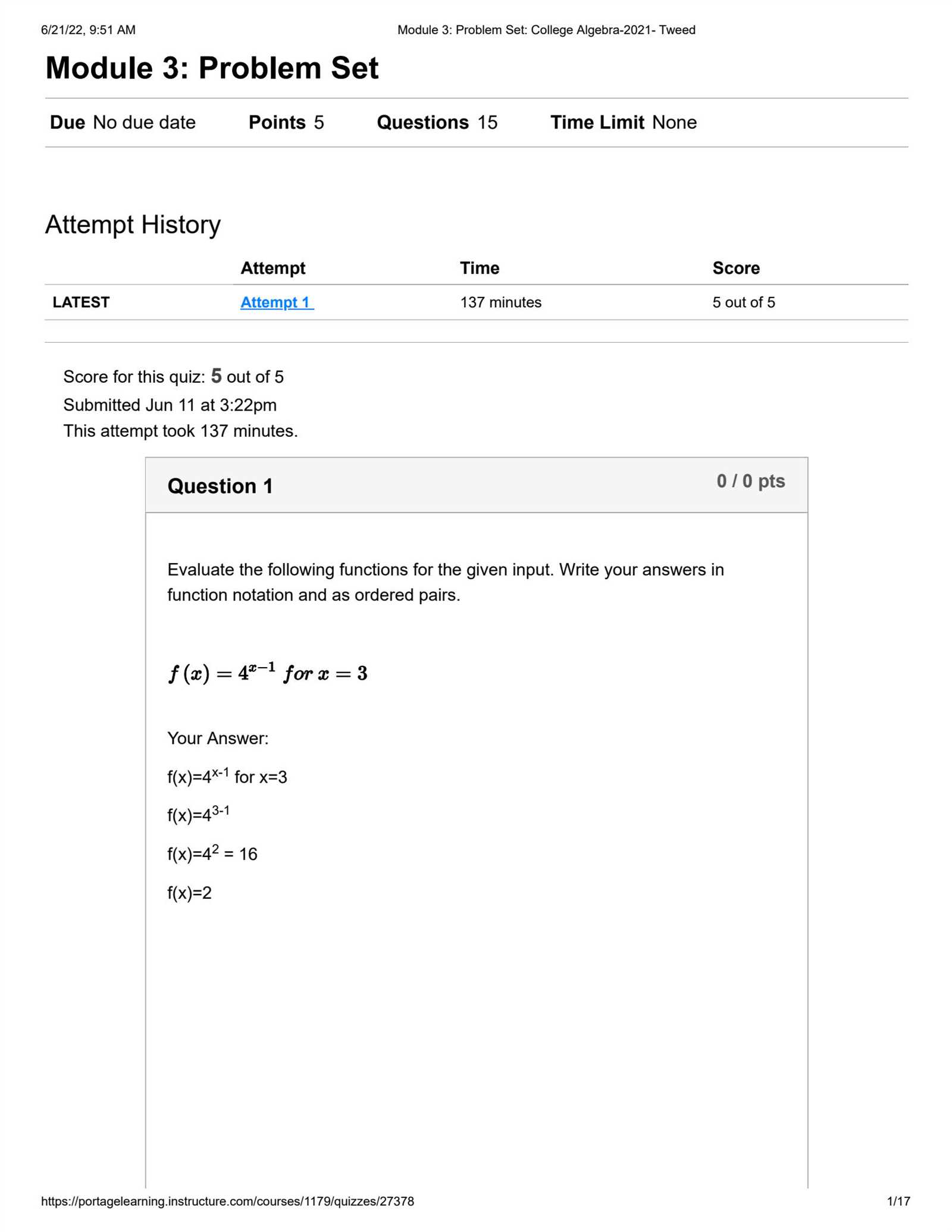
Understanding the core principles of solving equations and graphing relationships is essential to succeeding in this area of mathematics. The third section focuses on providing clarity and a deeper understanding of the methods used to tackle these problems effectively.
Whether you are dealing with linear relationships, inequalities, or systems of equations, this guide offers a comprehensive approach to navigating through the challenges. By breaking down complex problems into smaller steps, it becomes easier to grasp the techniques that will support your learning journey.
Practice and application play a crucial role in reinforcing your skills, and with the right resources, you can easily build confidence in solving various mathematical scenarios. This section is designed to help you gain mastery through clear explanations and practical exercises that will guide you through every step.
Algebra 1 Module 3 Answers
This section focuses on developing the necessary skills to solve various mathematical problems efficiently. By mastering key techniques, you will be able to approach equations with confidence, making it easier to handle more complex topics in the future.
Understanding Linear Equations
Linear equations represent relationships between variables with a constant rate of change. These equations often take the form of y = mx + b, where m is the slope and b is the y-intercept. To solve these equations, you need to isolate the variable and find its value by applying simple operations. Below is an example of solving a linear equation:
| Equation | Step 1 | Step 2 | Solution |
|---|---|---|---|
| 2x + 3 = 11 | Subtract 3 from both sides | 2x = 8 | x = 4 |
Solving Systems of Equations
Systems of equations involve solving for multiple variables at the same time. This often requires using substitution or elimination methods to find the values that satisfy both equations simultaneously. The following example demonstrates the substitution method:
| Equation 1 | Equation 2 | Substitution Step | Solution |
|---|---|---|---|
| y = 2x + 3 | 3x + y = 12 | Substitute y from Equation 1 into Equation 2 | x = 3, y = 9 |
Key Concepts in Algebra 1 Module 3
In this section, you’ll explore the foundational ideas that form the backbone of solving linear relationships and working with equations. Understanding these core principles is essential to progressing to more complex mathematical concepts. By applying these concepts, you’ll develop the ability to manipulate expressions, solve for unknowns, and interpret solutions in real-world contexts.
Linear Relationships and Equations
Linear equations describe relationships between variables with a constant rate of change. These equations are often represented in the form y = mx + b, where m is the slope and b is the y-intercept. To solve for a specific variable, it’s crucial to manipulate the equation step by step. A solid understanding of these concepts is necessary for graphing lines and interpreting real-world data that follows a straight-line pattern.
Solving and Graphing Inequalities
Inequalities provide a way to express ranges of possible solutions, rather than just one exact value. By working with inequalities, you can represent a variety of outcomes, such as x > 3 or y ≤ 2x + 5. Understanding how to graph these expressions on a coordinate plane and solve them algebraically is key to mastering this concept. It’s important to pay attention to the direction of the inequality sign when performing operations to ensure correct solutions.
Step-by-Step Solutions for Exercises
Breaking down mathematical problems into smaller, manageable steps is crucial for understanding the process and finding accurate solutions. This section will guide you through solving various types of exercises, helping you understand the logic behind each step and giving you the confidence to solve similar problems on your own.
Solving Linear Equations
To solve linear equations, start by isolating the variable on one side of the equation. Follow these steps to solve an equation like 3x – 4 = 8:
- Add 4 to both sides: 3x = 12
- Divide both sides by 3: x = 4
By carefully following each step, you can easily solve for the unknown variable and check your solution for accuracy.
Graphing Linear Inequalities
Graphing linear inequalities requires plotting a line and shading the appropriate region that represents the solution. Here’s a step-by-step guide for solving and graphing the inequality y > 2x + 1:
- Start by graphing the line y = 2x + 1 as if it were an equation.
- Since the inequality is “greater than” (>), draw a dashed line to indicate that points on the line are not included in the solution.
- Shade the region above the line, since “greater than” means the solution includes all values above the line.
These clear steps ensure you graph the inequality correctly and interpret the solution effectively.
Understanding Linear Equations and Functions
Linear relationships describe how one quantity changes in direct proportion to another. These relationships are expressed through equations that establish a constant rate of change between the variables. Understanding how to manipulate and interpret these equations is essential for solving problems involving direct proportionality, graphing lines, and predicting future values.
Key Features of Linear Equations

A linear equation is typically represented in the form y = mx + b, where m represents the slope and b is the y-intercept. The slope indicates how steep the line is, while the y-intercept tells us where the line crosses the y-axis. To solve these equations, you often isolate the variable to find the value of y or x, depending on which one you are solving for.
Graphing Linear Functions
Graphing a linear function involves plotting points on a coordinate plane and connecting them to form a straight line. To graph an equation like y = 3x + 2, start by identifying the y-intercept (2) and plotting that point on the y-axis. Then, use the slope (3) to find the next point by moving up 3 units and to the right 1 unit. Connect these points, and you’ll have a straight line that represents the function.
How to Solve Systems of Equations
Solving systems of equations involves finding the values of variables that satisfy multiple equations simultaneously. This process is essential when you need to solve problems that involve two or more conditions that must be true at the same time. There are several methods to approach these types of problems, including substitution, elimination, and graphing, each suited to different scenarios.
The substitution method involves solving one equation for one variable and then substituting that expression into the other equation. This approach reduces the system to a single equation with one variable, making it easier to solve. The elimination method, on the other hand, focuses on adding or subtracting equations to eliminate one variable at a time, simplifying the process of solving for the remaining variables.
Each method offers its advantages depending on the structure of the equations. Choosing the right technique can significantly streamline the process and lead to a quicker solution.
Tips for Solving Word Problems
Word problems can often seem daunting because they require translating real-world situations into mathematical equations. The key to solving these problems efficiently is breaking them down into manageable steps and identifying the important information. By focusing on the problem’s structure and methodically working through the conditions, you can develop a clear path to the solution.
Identify Key Information
The first step in solving any word problem is to carefully read through the given information and highlight the essential details. Focus on numbers, units, and key phrases that describe the relationships between variables. This will help you translate the situation into a mathematical equation. For example, if a problem mentions a “rate of change,” you’ll need to recognize how this affects the equation and how to express it mathematically.
Set Up the Equation
Once you’ve identified the key information, it’s time to set up an equation based on the problem’s context. Be sure to define your variables clearly, using symbols like x or y to represent unknown quantities. For example, if the problem asks for the total cost of items at a certain price per unit, you might set up the equation as total cost = price per unit × number of units. After setting up the equation, you can then proceed with solving it just as you would with any other mathematical problem.
Common Mistakes to Avoid in Module 3
When working through exercises in this section, it’s easy to make simple errors that can lead to incorrect solutions. These mistakes often stem from misunderstandings of concepts or overlooking key steps in the problem-solving process. By recognizing and avoiding these common pitfalls, you can improve your accuracy and efficiency when tackling similar problems.
Misinterpreting the Problem
One of the most frequent errors occurs when the problem is not read carefully. Missing important details or misinterpreting the question can result in solving for the wrong variable or using incorrect operations. Take the time to fully understand the problem before jumping into the solution. Underlining or highlighting important information can help ensure you’re addressing the right question.
Incorrectly Applying Operations

Another common mistake is misapplying mathematical operations, such as incorrectly adding or subtracting terms when solving equations. Always double-check your steps, especially when working with negative numbers or fractions. It’s essential to follow the correct order of operations and ensure that each step is executed properly to avoid compounding errors.
How to Graph Linear Equations
Graphing linear equations is a fundamental skill that allows you to visualize the relationship between variables. The process involves plotting points on a coordinate plane and drawing a straight line that represents the equation. Understanding how to correctly interpret the equation and apply it to the graphing process will help you create accurate visual representations of linear relationships.
Steps to Graph a Linear Equation
Follow these steps to graph an equation like y = 2x + 3:
- Identify the y-intercept: In this case, the y-intercept is 3. This is where the line crosses the y-axis, so plot the point (0, 3).
- Determine the slope: The slope of this equation is 2, meaning the line rises 2 units for every 1 unit it moves to the right. From the y-intercept, use the slope to plot the next point.
- Plot a second point: Starting at (0, 3), move up 2 units and 1 unit to the right to plot the point (1, 5).
- Draw the line: Connect the two points with a straight line, extending it in both directions to represent the entire equation.
Using the Slope-Intercept Form
When working with linear equations in the slope-intercept form y = mx + b, m represents the slope and b represents the y-intercept. This form makes graphing easier because you can directly identify these values. Once the first point is plotted at the y-intercept, use the slope to plot additional points and draw the line.
Solving Inequalities in Algebra 1
Solving inequalities involves finding the range of values that satisfy a given condition. Unlike equations, which provide a specific solution, inequalities express a range of possible solutions, often represented graphically or symbolically. Understanding the rules for manipulating inequalities is crucial for solving them correctly and interpreting the results in context.
Steps for Solving Linear Inequalities

Follow these steps to solve linear inequalities like 2x + 3 > 7:
- Isolate the variable: Start by moving constants to the other side of the inequality. In this case, subtract 3 from both sides: 2x > 4.
- Divide by the coefficient: To isolate x, divide both sides by 2: x > 2.
- Graph the solution: On a number line, plot the solution. Since this inequality is strict (>), represent the solution with an open circle at 2, indicating that 2 is not included.
Key Considerations When Solving Inequalities
- Flipping the inequality sign: If you multiply or divide both sides of an inequality by a negative number, you must flip the inequality sign. For example, -2x < 6 becomes x > -3 when dividing by -2.
- Double-checking the solution: Always verify that the solution fits the original inequality. Test a number within the solution range to confirm the result is correct.
Understanding Slope and Intercept
The concepts of slope and intercept are fundamental to understanding how linear relationships are represented in mathematical equations. The slope tells you how steep a line is, while the intercept provides the point where the line crosses the vertical axis. Together, these two components define the behavior of a line and help describe the relationship between two variables in various contexts.
Slope is often described as the “rate of change” between the two variables. It tells you how much the dependent variable changes for every unit increase in the independent variable. Intercept, on the other hand, represents the value of the dependent variable when the independent variable is zero. This is the starting point or reference point of the line on the graph.
By understanding both slope and intercept, you can quickly graph linear equations and interpret the relationships they represent. These concepts are crucial for solving real-world problems that involve proportional relationships, rates, and changes over time.
Real-World Applications of Algebra 1
The concepts learned in this section are not just limited to the classroom–they have real-world applications that are essential for problem-solving in many different fields. From finance to engineering, the ability to understand and manipulate relationships between variables is crucial. Whether it’s calculating costs, predicting outcomes, or optimizing processes, the skills gained through solving equations and working with variables can be applied to everyday life and professional scenarios.
For instance, businesses use these principles to create budgets, manage inventory, and forecast sales. In engineering, equations help to model structures, determine load limits, and design efficient systems. Even in personal finance, understanding how to work with percentages and calculate interest can save money and guide investment decisions.
As you progress in your studies, you’ll discover how the mathematical tools you develop in this area translate directly into meaningful solutions for challenges in a wide range of industries and daily activities.
Using Substitution and Elimination Methods
Solving systems of equations can often be achieved through different techniques, two of the most common being substitution and elimination. These methods allow you to find the values of variables that satisfy multiple equations simultaneously. Each approach has its advantages, and knowing when and how to apply them is essential for effective problem-solving.
Substitution Method
The substitution method involves solving one of the equations for one variable and then substituting this expression into the other equation. This reduces the system to a single equation with one variable, which can be solved more easily.
- Choose one equation and solve for one variable in terms of the other.
- Substitute this expression into the second equation.
- Solve the resulting equation and find the value of one variable.
- Substitute the value back into the original equation to find the other variable.
Elimination Method
The elimination method works by adding or subtracting the equations to eliminate one of the variables. This method is particularly useful when the coefficients of one variable are the same or opposites in both equations.
- Align the equations so that the variables are in the same order.
- Multiply the equations if necessary to make the coefficients of one variable match or cancel each other.
- Add or subtract the equations to eliminate one variable.
- Solve the resulting equation for the remaining variable and substitute back to find the other variable.
How to Check Your Answers
Verifying your solutions is an essential part of solving any mathematical problem. After completing a problem, it’s important to go back and check that your results are correct. This not only helps to ensure accuracy but also builds confidence in your ability to work through similar problems in the future.
Substitute Your Solution Back
One of the most effective ways to check your work is by substituting your solution back into the original equations. This will allow you to verify if the values you’ve found truly satisfy all the conditions set by the problem. If both sides of the equation are equal after substitution, then your solution is correct.
Cross-Check with Other Methods
Another method to verify your solution is to use a different technique to solve the same problem. For example, if you initially used substitution to find a solution, try using elimination instead, or vice versa. If both methods yield the same result, you can be more confident in the accuracy of your answer.
Best Study Practices for Module 3
To master the concepts covered in this section, it’s crucial to follow effective study habits that promote understanding and retention. Developing a structured approach can help you better grasp the material and apply it to solve problems efficiently. The following strategies will guide you through the learning process and improve your overall performance.
Active Practice and Problem Solving
Practice is key to mastering any mathematical concept. Work through a variety of problems to reinforce your understanding. Begin with simpler problems and gradually move on to more complex ones as you gain confidence. Active practice ensures that you are not just memorizing formulas but truly understanding how to apply them in different scenarios.
Review Mistakes and Learn from Them
When you make errors, take the time to carefully review them. Analyze where things went wrong and try to identify patterns in your mistakes. This will help you avoid making the same mistakes in the future. By learning from errors, you’ll develop a deeper understanding of the concepts and improve your problem-solving skills.
Using Online Tools for Algebra Help
In today’s digital age, there is a wide range of online tools available that can significantly aid in understanding mathematical concepts. These resources can offer step-by-step solutions, interactive practice problems, and even instant feedback, making it easier to grasp difficult topics and improve performance. Utilizing these tools effectively can enhance your learning experience and provide additional support outside of the classroom.
Types of Online Resources
There are several types of online platforms that can help you with your studies. Here are a few to consider:
- Interactive Problem Solvers: Websites and apps where you input equations and receive detailed solutions with explanations.
- Video Tutorials: Educational channels that break down complex problems and show how to solve them step-by-step.
- Practice Exercises: Online platforms offering a wide range of practice problems to test your skills and track your progress.
- Forums and Discussion Groups: Communities where you can ask questions, share insights, and learn from others’ experiences.
Maximizing the Use of Online Tools
To get the most out of these online tools, consider the following tips:
- Start with the Basics: Ensure that you understand the foundational concepts before diving into more advanced topics.
- Use Multiple Sources: Cross-reference information across different platforms to get a well-rounded understanding of the material.
- Practice Regularly: Consistent use of these tools will reinforce what you’ve learned and help solidify your skills.
Review of Key Terms and Definitions
To fully understand mathematical problems and their solutions, it is crucial to have a clear grasp of the essential terms and definitions. These concepts form the foundation for solving various types of problems and allow you to approach challenges systematically. A solid understanding of these key terms helps to simplify complex equations and better navigate through the steps of problem-solving.
| Term | Definition |
|---|---|
| Variable | A symbol, usually a letter, used to represent a number in an equation or expression. |
| Coefficient | A numerical factor in a term that is multiplied by a variable. |
| Equation | A mathematical statement that shows the equality of two expressions, separated by an equal sign. |
| Expression | A mathematical phrase that can contain numbers, variables, and operators but does not have an equal sign. |
| Constant | A fixed value that does not change. |
| Linear Equation | An equation where the highest power of the variable is one, resulting in a straight-line graph when plotted. |
| Intercept | The point at which a line crosses the y-axis or x-axis on a graph. |
Resources for Additional Practice
To truly master any mathematical concept, consistent practice is essential. Fortunately, there are numerous resources available that provide additional exercises, examples, and explanations to help reinforce your skills. Whether you’re looking for interactive websites, printable worksheets, or video tutorials, these tools offer valuable opportunities to strengthen your understanding and improve your problem-solving abilities.
Online Practice Platforms
- Khan Academy: Offers interactive lessons, practice problems, and video tutorials on a wide range of topics.
- Wolfram Alpha: Provides step-by-step solutions for various mathematical problems and allows you to explore detailed explanations.
- IXL: An online platform offering personalized practice in mathematics with immediate feedback to track progress.
Books and Worksheets
- Practice Workbooks: Many publishers offer comprehensive workbooks that focus on specific areas of study, providing exercises and solutions.
- Math Lab Books: These books offer a variety of problems to work through, along with solutions to help reinforce the learning process.
- Online Worksheets: Websites like Teachers Pay Teachers offer free and paid downloadable worksheets on various topics.
Utilizing these resources can provide a well-rounded approach to mastering key concepts and boost your confidence when tackling mathematical problems.