
In this section, we dive into the core concepts that will enhance your understanding of mathematical principles. The problems covered are designed to strengthen your ability to apply fundamental techniques in a variety of scenarios. Whether you’re solving equations, working with expressions, or graphing data, the skills learned here will serve as a solid foundation for further mathematical study.
Through practice and analysis, you will gain a deeper insight into the strategies that make problem-solving easier and more effective. With each problem set, you will build confidence and the ability to approach new challenges with a clearer perspective. The solutions provided guide you through the process step by step, ensuring that no detail is overlooked.
As you progress, you’ll recognize patterns and methods that will streamline your work. By mastering these techniques, you will be prepared to tackle more complex problems with ease, whether in an academic setting or in practical applications. Success in mathematics is about persistence and clarity, and this section is designed to help you achieve both.
Mathematical Solutions for Chapter 6
In this section, we explore a set of essential problems and their detailed solutions, focusing on strengthening your problem-solving skills. By working through each example, you’ll develop a deeper understanding of the strategies needed to solve a wide range of equations and expressions. These exercises provide the perfect opportunity to reinforce your knowledge and gain confidence in applying these concepts.
Step-by-Step Problem Solving
Each problem is broken down into smaller, manageable steps, allowing you to follow along and grasp the reasoning behind every solution. By approaching each challenge methodically, you will be able to recognize common techniques used across different types of questions. This approach ensures a comprehensive understanding and makes it easier to apply similar methods in future problems.
Common Mistakes and How to Avoid Them
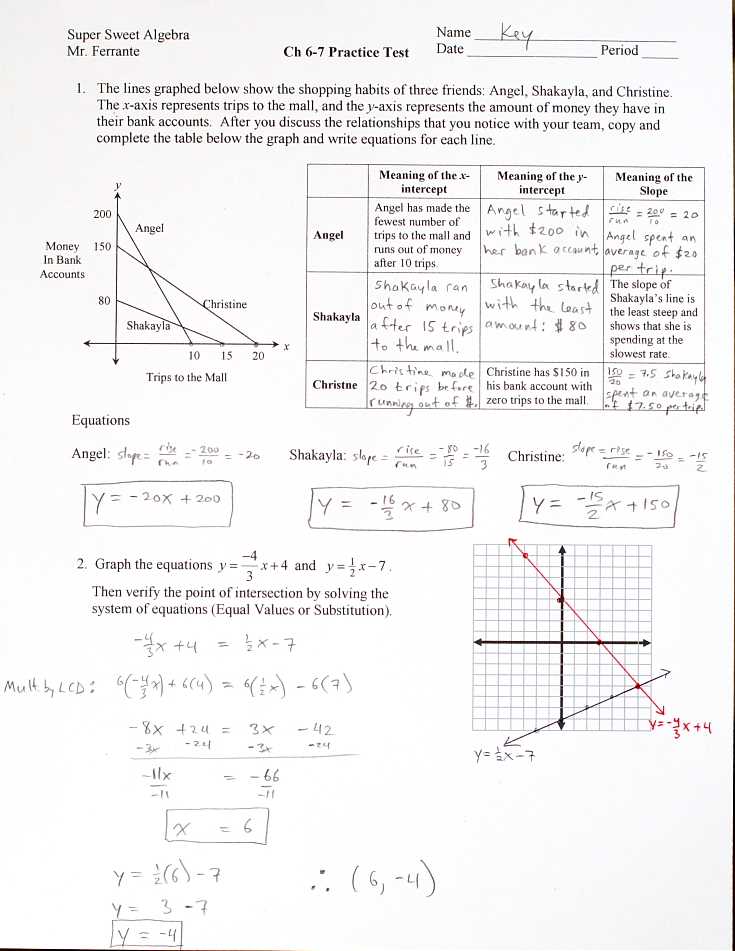
As you review the solutions, you will also identify some of the most frequent errors students make when tackling these types of problems. Understanding these mistakes and knowing how to avoid them is crucial to improving your accuracy and efficiency. Through careful analysis of the steps and solutions, you will be better equipped to spot pitfalls and approach future problems with more precision.
Understanding Key Concepts in Chapter 6
In this section, we focus on the foundational principles and techniques that are essential for tackling the exercises and problems effectively. The goal is to provide a clear understanding of the core ideas that will help you solve a variety of mathematical challenges. By grasping these concepts, you will be better prepared to work through problems with confidence and accuracy.
Core Techniques to Master

Several key methods are central to mastering the material in this section. These techniques, once fully understood, can be applied to a wide range of problems, making them invaluable tools for solving complex tasks. Below are some important concepts to focus on:
- Identifying patterns and relationships between variables.
- Breaking down equations into simpler parts for easier manipulation.
- Understanding the importance of balancing both sides of an equation.
- Recognizing different types of expressions and how to handle them.
Important Strategies for Success
To make the most of these fundamental principles, it’s essential to approach each problem with a strategic mindset. Here are some effective strategies:
- Work through problems step by step, ensuring each part is understood before moving on.
- Check your solutions by substituting values back into the original problem to verify accuracy.
- Practice regularly to reinforce your understanding and speed up your problem-solving ability.
- Review common mistakes and learn from them to avoid repeating them in the future.
By mastering these key concepts and strategies, you will develop a strong foundation for solving more advanced problems and achieving success in this area of study.
Step-by-Step Solutions for Practice Problems
This section provides detailed explanations for solving practice problems, breaking down each step to ensure a comprehensive understanding of the process. By following these solutions closely, you will be able to identify the methods used and apply them to similar challenges. The step-by-step approach ensures clarity and allows for better retention of the techniques required to solve various problems effectively.
Understanding the Process
Each solution is outlined with careful attention to detail, highlighting key concepts and providing clear reasoning at every stage. The goal is to make sure every step is well-understood before proceeding to the next one. Below is an overview of the typical steps involved in solving problems:
- Identify the variables and constants involved in the problem.
- Apply the appropriate formula or method based on the problem type.
- Manipulate the equation or expression carefully to isolate the desired variable.
- Double-check calculations and simplify the result where possible.
Common Techniques for Problem Solving
Throughout the step-by-step solutions, several techniques are consistently applied. These techniques are crucial for approaching and solving similar problems efficiently:
- Breaking down complex problems into smaller, manageable parts.
- Rearranging terms and using properties of equality to simplify expressions.
- Substituting known values to verify the solution.
- Ensuring logical consistency and accuracy in each step.
By practicing these strategies, you will enhance your problem-solving skills and build a stronger foundation for tackling more advanced exercises.
Common Mistakes in Chapter 6 Explained
While working through problems, it’s easy to make errors that can lead to incorrect solutions. Recognizing and understanding these common mistakes is essential to improving problem-solving skills. In this section, we will explore some of the most frequent errors and how to avoid them, ensuring that you can approach each task with greater accuracy and confidence.
Common Errors in Mathematical Operations
One of the main sources of mistakes is incorrect application of mathematical operations. This can happen when the wrong order of operations is followed or when terms are not simplified correctly. Some of the most common errors include:
- Misapplying the distributive property.
- Incorrectly handling negative signs or parentheses.
- Forgetting to perform a necessary step, such as isolating a variable.
- Overlooking the need to simplify both sides of an equation equally.
Conceptual Mistakes to Watch For
Sometimes mistakes stem from a misunderstanding of the underlying concepts rather than from mathematical procedures. These errors can be trickier to catch because they involve misinterpreting the problem itself. Some examples include:
- Confusing the relationship between variables and constants.
- Misunderstanding how to apply formulas for different types of problems.
- Failing to check for extraneous solutions in certain equations.
- Not recognizing when an equation has multiple valid solutions.
By becoming aware of these common pitfalls and understanding how to avoid them, you will improve your accuracy and efficiency when solving mathematical problems.
How to Approach Algebraic Equations
Solving equations involves more than just applying formulas–it requires a structured approach to ensure accuracy and efficiency. The key to mastering equations lies in understanding the relationships between variables and constants, and applying logical steps to isolate the unknown. By following a systematic process, you can simplify even the most complex equations and solve them with confidence.
The first step is to carefully read the equation and identify the terms and operations involved. It’s essential to recognize what each term represents and how they relate to one another. Once you’ve identified the variables and constants, you can begin applying appropriate methods to isolate the unknown variable.
Next, focus on simplifying the equation step by step. This may involve moving terms to one side, combining like terms, or performing basic operations such as addition, subtraction, multiplication, or division. The goal is to gradually isolate the variable while maintaining the equality of both sides of the equation.
Finally, always check your solution by substituting it back into the original equation. This ensures that the solution is correct and satisfies all conditions of the problem. Regular practice and familiarity with common techniques will help you approach each equation with clarity and precision.
Mastering the Techniques for Factoring
Factoring is a crucial skill in mathematics that allows you to break down complex expressions into simpler components. By mastering the techniques for factoring, you can simplify equations and make solving problems more manageable. This process is essential for solving quadratic expressions, finding roots, and working with polynomials.
To successfully factor expressions, it is important to understand the different methods available. These techniques range from identifying common factors to applying specific formulas for special cases. By recognizing the structure of the expression, you can choose the most efficient method for factoring.
Key Techniques for Factoring

Here are some essential techniques to focus on when learning how to factor:
- Look for common factors in all terms, such as numbers or variables, and factor them out.
- Recognize difference of squares and use the formula (a? – b?) = (a – b)(a + b).
- Apply factoring by grouping for expressions with four terms by grouping pairs and factoring each group.
- Use the quadratic formula or completing the square when dealing with quadratic expressions.
Practice and Application
To gain proficiency in factoring, consistent practice is essential. Work through different types of problems and apply the appropriate method to each. With time, you will be able to quickly recognize patterns and factor expressions with ease. Below are some tips to improve your factoring skills:
- Always check for the greatest common factor first.
- Practice factoring quadratic expressions and polynomials regularly.
- Work on problems with varying degrees of difficulty to build your confidence.
By mastering these factoring techniques, you’ll be better equipped to tackle more complex mathematical problems and strengthen your overall problem-solving abilities.
Real-Life Applications of Algebraic Concepts

The concepts explored in this section are not just theoretical–they have practical applications in various aspects of everyday life. From managing personal finances to understanding scientific phenomena, the ability to solve equations and manipulate expressions is a valuable skill that can be applied in many real-world situations. This section highlights how these mathematical techniques are used beyond the classroom, demonstrating their importance in numerous fields.
Everyday Financial Decisions
One of the most common applications of these mathematical concepts is in managing personal finances. Whether it’s calculating interest rates, planning a budget, or determining loan payments, the ability to work with equations is essential. For instance, if you’re taking out a loan, you can use equations to calculate monthly payments based on the loan amount, interest rate, and duration. Understanding how to manipulate these formulas allows you to make informed financial decisions and avoid costly mistakes.
Applications in Engineering and Technology
In fields like engineering, technology, and physics, the same principles are used to solve complex problems. Engineers rely on equations to design structures, optimize systems, and ensure safety. For example, when designing bridges or buildings, they use algebraic formulas to calculate load distribution, material strength, and overall stability. Similarly, in technology, algorithms and coding often involve mathematical operations that allow devices and software to function correctly.
By applying these methods in real-life situations, you can see how the mathematical techniques you learn can improve decision-making and problem-solving in various aspects of life and work.
Solving Word Problems Effectively
Word problems often seem challenging because they require translating a narrative into a mathematical equation. The key to solving them efficiently is to break down the information, identify the unknowns, and systematically work towards the solution. By following a structured approach, you can easily transform a complex word problem into a solvable equation.
Start by carefully reading the problem and identifying the relevant information. Pay attention to key details, such as quantities, relationships, and what needs to be solved for. Once you have identified the variables, you can set up an equation or expression to represent the situation described in the problem.
Steps for Solving Word Problems

Follow these steps to solve word problems more effectively:
| Step | Action |
|---|---|
| 1 | Read the problem carefully and highlight important information. |
| 2 | Identify the unknowns and assign variables to them. |
| 3 | Translate the words into mathematical equations or expressions. |
| 4 | Perform calculations and simplify the equation as needed. |
| 5 | Check your solution by plugging it back into the original problem. |
By following these steps, you can approach each word problem systematically, ensuring that you don’t miss any critical details. Practice is essential to becoming more proficient at solving these types of problems, and with time, you’ll find that the process becomes more intuitive.
Important Formulas in Algebraic Concepts
Mathematical formulas are essential tools for solving problems efficiently. Understanding and applying the correct formulas can simplify complex tasks, whether you’re dealing with equations, polynomials, or geometric shapes. These formulas act as shortcuts, enabling you to quickly arrive at solutions without unnecessary steps.
There are several key formulas that are frequently used in a wide range of mathematical problems. Mastering these can help you solve problems faster and with greater accuracy. Some of the most commonly used formulas include those for solving quadratic equations, factoring expressions, and calculating areas and volumes.
Key Formulas to Remember
Here are some essential formulas that are useful across various topics:
- Quadratic Formula: Used to solve quadratic equations in the form ax? + bx + c = 0.
x = (-b ± v(b? – 4ac)) / 2a - Difference of Squares: A method for factoring expressions in the form a? – b?.
(a – b)(a + b) - Distributive Property: Helps simplify expressions involving multiplication.
a(b + c) = ab + ac - Area of a Rectangle: Used to find the area of a rectangle.
Area = length ? width - Volume of a Cube: Used to calculate the volume of a cube.
Volume = side?
These formulas are fundamental to a wide variety of mathematical operations and problem-solving scenarios. By familiarizing yourself with these key formulas, you can tackle a wide range of problems with greater ease and efficiency.
Exploring Functions and Their Properties
Functions are a core concept in mathematics, providing a way to relate one set of values to another. They help describe how one quantity depends on another, which makes them essential in understanding relationships and patterns in various fields. By analyzing their properties, we can gain insights into the behavior of different systems and solve complex problems more effectively.
In this section, we will explore the different types of functions, their key characteristics, and how to analyze their behavior. Understanding the properties of functions allows us to manipulate and solve problems involving variables, equations, and inequalities.
Key Properties of Functions
The following are the primary properties of functions that are important for solving problems:
| Property | Definition |
|---|---|
| Domain | The set of all possible input values (x-values) for which the function is defined. |
| Range | The set of all possible output values (y-values) produced by the function. |
| Continuity | Refers to whether a function has any breaks, holes, or jumps in its graph. |
| Injectivity | A function is injective if each output is produced by exactly one input. |
| Symmetry | Describes whether a function has a balanced or mirrored shape, often across the y-axis or origin. |
By studying these properties, you can better understand how a function behaves and how to use it in real-world applications. Functions play a critical role in many areas, including economics, engineering, and computer science, making them a valuable tool for problem-solving and analysis.
Reviewing Key Skills from Previous Chapters
Mastering new mathematical concepts often requires revisiting and reinforcing the skills learned earlier. Revising key skills from previous lessons helps solidify your understanding, making it easier to tackle more advanced topics. By ensuring a firm grasp of foundational techniques, you can approach new challenges with confidence and clarity.
In this section, we’ll revisit essential skills that are frequently used and are critical to succeeding in more complex problem-solving tasks. These skills are the building blocks that help simplify more difficult concepts, making them easier to understand and apply.
Essential Skills to Reinforce
Here are some crucial skills from previous lessons that form the foundation for tackling more advanced topics:
- Solving Linear Equations: Understanding how to manipulate equations and solve for unknown variables is essential for progressing in mathematics.
- Factoring Expressions: Recognizing how to break down complex expressions into simpler factors allows for easier manipulation and simplification.
- Working with Fractions: Mastery of operations involving fractions is fundamental to solving a wide range of problems.
- Understanding Graphs: Knowing how to plot and interpret graphs helps visualize mathematical relationships and make sense of data.
Reinforcing Core Techniques

Consistently practicing these key techniques will enhance your problem-solving abilities. By reviewing and applying these skills regularly, you’ll build a strong foundation that will support your progress through more advanced topics.
Tips for Preparing for Math Tests
Preparing for a math test can feel overwhelming, but with the right strategies, you can approach the exam with confidence. Effective preparation involves reviewing key concepts, practicing problem-solving techniques, and managing your time efficiently. The more familiar you are with the material, the better equipped you’ll be to tackle challenging problems on test day.
In this section, we will explore several tips that can help you prepare effectively for your math exams. These tips focus on improving understanding, practicing regularly, and creating a solid study plan to ensure you’re ready when the test comes.
Effective Study Strategies

Here are some proven techniques to help you study for your math tests:
| Strategy | Details |
|---|---|
| Understand Key Concepts | Rather than memorizing formulas, focus on understanding the underlying principles behind the problems. This helps you apply concepts to different situations. |
| Practice Regularly | Work through a variety of practice problems. The more problems you solve, the more comfortable you’ll become with different types of questions. |
| Review Mistakes | Go back to problems you got wrong and analyze why you made mistakes. This can help you identify areas where you need more practice or clarification. |
| Use Study Guides | Study guides and past tests can be valuable tools for reviewing important concepts. These resources help you get familiar with the format and types of questions you may encounter. |
Time Management Tips
When preparing for a test, it’s crucial to manage your study time efficiently. Allocate enough time to cover all relevant topics and take breaks to avoid burnout. Try the following:
- Start Early: Give yourself plenty of time to review the material. Cramming the night before is less effective than spreading out your study sessions over time.
- Prioritize Topics: Focus on areas where you feel less confident. Spend extra time on these topics while also reviewing stronger areas.
- Take Breaks: Short breaks during study sessions help improve focus and prevent fatigue. Try working for 25-30 minutes followed by a 5-minute break.
By following these tips, you’ll increase your chances of performing well on your math test and reduce the stress that often accompanies exam preparation.
How to Improve Problem-Solving Speed
Improving your problem-solving speed is an essential skill that can greatly enhance your efficiency, especially when faced with time-limited tests or assignments. Speed in solving mathematical problems comes with practice, strategic thinking, and the ability to recognize patterns. The more you practice and familiarize yourself with various problem types, the faster and more confidently you can work through them.
In this section, we’ll discuss practical techniques to help you increase your problem-solving speed, allowing you to tackle questions more quickly and accurately.
Mastering Key Concepts and Techniques
One of the best ways to increase problem-solving speed is by mastering the essential concepts and techniques that appear frequently in problems. This allows you to handle similar questions with ease, as you’ll be able to quickly identify the best approach. Here are a few tips to help you:
- Know the Basics: Ensure that you have a strong grasp of fundamental techniques like solving equations, simplifying expressions, and manipulating fractions.
- Recognize Patterns: Many problems follow similar patterns. By practicing regularly, you will begin to recognize common patterns and apply known methods more efficiently.
- Break Down Complex Problems: When faced with a challenging problem, break it into smaller, more manageable parts. This reduces the complexity and makes the problem easier to solve quickly.
Speed Techniques for Practice
In addition to mastering core concepts, practicing specific techniques can also help you improve your speed. Try the following approaches:
- Time Yourself: Set a timer while practicing problems to get used to working within a time limit. This will train your brain to think and act more quickly under pressure.
- Use Mental Math: For simpler calculations, rely on mental math instead of writing out every step. This can save time and improve your overall efficiency.
- Skip and Return: If you encounter a difficult question, don’t dwell on it for too long. Move on to easier questions and return to the tough ones later with a fresh perspective.
By following these strategies and incorporating them into your practice routine, you’ll steadily improve your ability to solve problems faster and with greater accuracy.
Understanding Algebraic Expressions in Depth

To master mathematical problems, a deep understanding of mathematical expressions is crucial. These expressions serve as the building blocks for many types of equations, and they are essential for solving a variety of mathematical challenges. By understanding how to interpret and manipulate these expressions, you gain the ability to approach complex problems with confidence.
In this section, we will explore the core components of mathematical expressions, providing you with a detailed understanding of how to work with them and utilize them effectively in problem-solving scenarios.
Breaking Down Mathematical Expressions
Mathematical expressions consist of numbers, variables, and operators that work together to represent a specific value or relationship. By carefully analyzing these components, you can begin to manipulate expressions in different ways to solve for unknowns or simplify complex terms.
- Variables: These represent unknown values and are typically denoted by letters such as x, y, or z. They are placeholders for specific numbers in an equation.
- Operators: These symbols, such as addition (+), subtraction (-), multiplication (*), and division (/), show the relationship between different parts of the expression.
- Constants: Constants are fixed values within an expression. These can be any number that does not change.
Techniques for Simplifying Expressions
Simplifying expressions is a key skill for tackling more complex problems. By reducing expressions to their simplest form, you can work with them more efficiently and find solutions more quickly. Here are some methods commonly used to simplify expressions:
- Combining Like Terms: When terms have the same variable, you can combine them to simplify the expression. For example, 3x + 4x becomes 7x.
- Distributive Property: This property allows you to expand expressions. For example, a(b + c) becomes ab + ac.
- Factoring: Factoring involves rewriting an expression as a product of its factors. This can help in solving equations or simplifying expressions further.
By mastering these techniques and understanding how expressions are structured, you will be well-equipped to handle a wide range of mathematical problems with greater ease and accuracy.
Graphing Techniques for Chapter 6 Problems
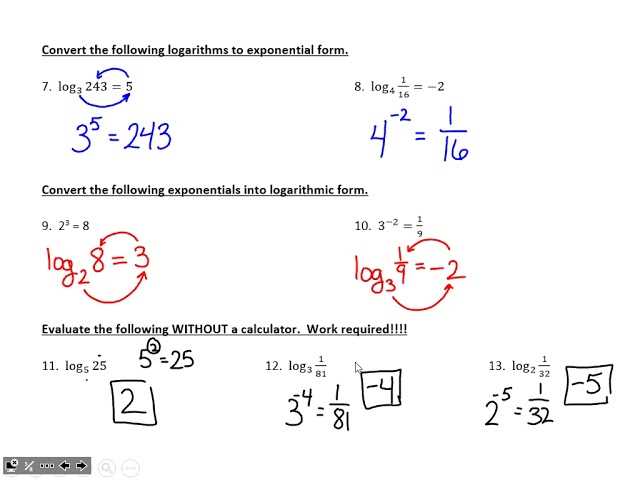
Understanding how to visualize equations and relationships is essential for solving mathematical problems efficiently. Graphing allows you to translate abstract equations into visual representations, helping to identify key features such as slopes, intercepts, and curves. Mastering graphing techniques enables you to approach problems more intuitively and make quicker decisions about how to solve them.
In this section, we will explore various graphing methods that are crucial for tackling problems in this section, from basic linear graphs to more complex functions.
Graphing Linear Equations

Linear equations are among the simplest to graph, as they produce straight lines on a coordinate plane. Here’s how to approach graphing a linear equation:
- Identify the slope and y-intercept: The general form of a linear equation is y = mx + b, where m is the slope and b is the y-intercept. These two values are essential for drawing the line.
- Plot the y-intercept: Start by plotting the point where the line crosses the y-axis (the value of b).
- Use the slope: The slope tells you how to move from the y-intercept. For example, a slope of 2 means you move up 2 units for every 1 unit you move to the right.
- Draw the line: Connect the points and extend the line in both directions.
Graphing Quadratic Functions
Quadratic functions create a parabola, which can be either upwards or downwards depending on the sign of the leading coefficient. Here are the steps for graphing a quadratic function:
- Identify the vertex: The vertex is the highest or lowest point of the parabola, depending on the direction it opens. For the equation y = ax? + bx + c, the x-coordinate of the vertex can be found using the formula x = -b/2a.
- Plot the vertex: Once you have the vertex, plot it on the graph.
- Determine the direction: If a is positive, the parabola opens upwards; if a is negative, it opens downwards.
- Plot additional points: Select values of x to calculate corresponding y-values, and plot these points to help shape the curve.
By following these graphing techniques, you can effectively represent a wide range of equations, making it easier to solve problems visually and find solutions more quickly.
Common Algebraic Mistakes to Avoid

Mathematical problems often present challenges that can lead to common errors if not approached carefully. Recognizing and avoiding these mistakes is key to mastering mathematical techniques and improving accuracy. In this section, we highlight some of the most frequent errors made when solving equations and simplify how to avoid them for better problem-solving.
From misapplying formulas to overlooking simple steps, these mistakes can drastically affect your results. Understanding the common pitfalls is essential for making more informed decisions while solving problems.
- Misunderstanding Operations with Parentheses: One of the most frequent mistakes occurs when operations inside parentheses are not simplified correctly. Always remember to handle operations within parentheses first, especially when they involve exponents or negative signs.
- Forgetting the Distribution of Negative Signs: A negative sign outside parentheses can be easily overlooked when expanding expressions. Ensure you distribute the negative sign to every term inside the parentheses. For example, – (x + 3) becomes -x – 3.
- Improper Handling of Fractions: When working with fractions, especially in equations, it’s essential to multiply both the numerator and denominator when simplifying. Common mistakes include cancelling terms incorrectly or applying operations unevenly across fractions.
- Incorrectly Combining Like Terms: A common error is incorrectly adding or subtracting like terms. Ensure that you only combine terms that have the same variable and exponent. For instance, 2x + 3x = 5x, not 5.
- Missing Units or Labels: In applied problems, failing to track units properly can lead to incorrect answers. Always include units, such as meters or seconds, and make sure they match across all terms.
- Overlooking Exponent Rules: Exponent rules such as the product rule (x^a * x^b = x^(a+b)) or quotient rule (x^a / x^b = x^(a-b)) can often be overlooked or misapplied, leading to mistakes in simplifying powers or solving exponential equations.
By being mindful of these mistakes and carefully following the steps in each problem, you can avoid common pitfalls and improve your ability to solve equations and problems accurately.
Resources for Extra Practice and Help
Mastering mathematical concepts requires consistent practice and the right resources. Whether you are reviewing material on your own or seeking further assistance, utilizing various tools can significantly enhance your understanding. In this section, we highlight some valuable resources that can provide extra practice, explanations, and support.
From online platforms to textbooks and interactive apps, there are many ways to reinforce learning and address specific challenges you may encounter. Accessing these resources can help clarify difficult topics, offer step-by-step solutions, and ensure you gain a deeper grasp of the material.
- Interactive Learning Websites: Websites such as Khan Academy, Coursera, and EdX offer comprehensive lessons, videos, and quizzes that allow you to practice different problem types and review key concepts.
- Online Problem Solvers: Platforms like Wolfram Alpha and Symbolab can help you solve equations and offer detailed explanations of each step, helping you understand the process behind the solution.
- Textbooks and Workbooks: Many textbooks provide practice problems at the end of each section, along with solutions and examples. Workbooks designed specifically for problem-solving practice are also a great option.
- Study Groups: Collaborating with classmates or joining a study group can be an effective way to exchange ideas and tackle challenging problems together. Group discussions often bring new perspectives to difficult topics.
- Private Tutors: If you need personalized support, hiring a tutor or attending office hours with your instructor can provide one-on-one help. Tutors can explain concepts in different ways until you achieve a better understanding.
- Math Apps: Downloading apps like Photomath or Mathway allows you to scan and solve problems, offering a quick solution along with detailed step-by-step guides to improve your problem-solving skills.
By exploring these resources, you can supplement your learning, gain extra practice, and receive the support you need to excel in your studies.
How to Keep Up with Chapter 6 Topics

Staying on top of complex subjects requires consistent effort, time management, and active engagement. To keep up with the material covered in this section, it’s essential to break down each concept into manageable chunks, practice regularly, and review consistently. By using a strategic approach, you can retain key information and tackle difficult topics with confidence.
One effective strategy is to set aside dedicated time each day to study and reinforce what you’ve learned. Regular practice is crucial for mastering any topic, as it helps solidify concepts and improve problem-solving skills. Additionally, it is beneficial to revisit previous lessons frequently to ensure the foundations are solid as you progress.
- Create a Study Schedule: Design a timetable that allocates time for review, practice, and new material. Stick to it and break your sessions into smaller, focused intervals to prevent burnout.
- Utilize Practice Problems: Solving a variety of problems is essential to reinforce what you’ve learned. Practice problems help you apply theoretical knowledge in different scenarios, deepening your understanding.
- Review Regularly: Regular revision helps consolidate your learning and ensures you remember key concepts when needed. Set aside time each week to revisit material and make notes of any areas where you need additional focus.
- Ask Questions: Don’t hesitate to ask for clarification if something is unclear. Whether it’s from a teacher, peer, or online resource, getting answers to your questions ensures you move forward with confidence.
- Join Study Groups: Studying in groups can offer different perspectives and help clarify difficult topics. Discussing problems with others often leads to a deeper understanding and provides the opportunity to share useful resources.
- Use Supplementary Resources: In addition to your textbooks, seek out extra materials like online tutorials, videos, or apps that explain topics in different ways to reinforce your learning.
By staying organized and dedicated, you can keep up with the material in this section and build a strong foundation for success in future topics.