
In this section, we explore fundamental principles and problem-solving techniques that are essential for mastering complex mathematical concepts. Understanding these concepts lays a strong foundation for tackling a wide range of challenges, from basic calculations to more advanced tasks.
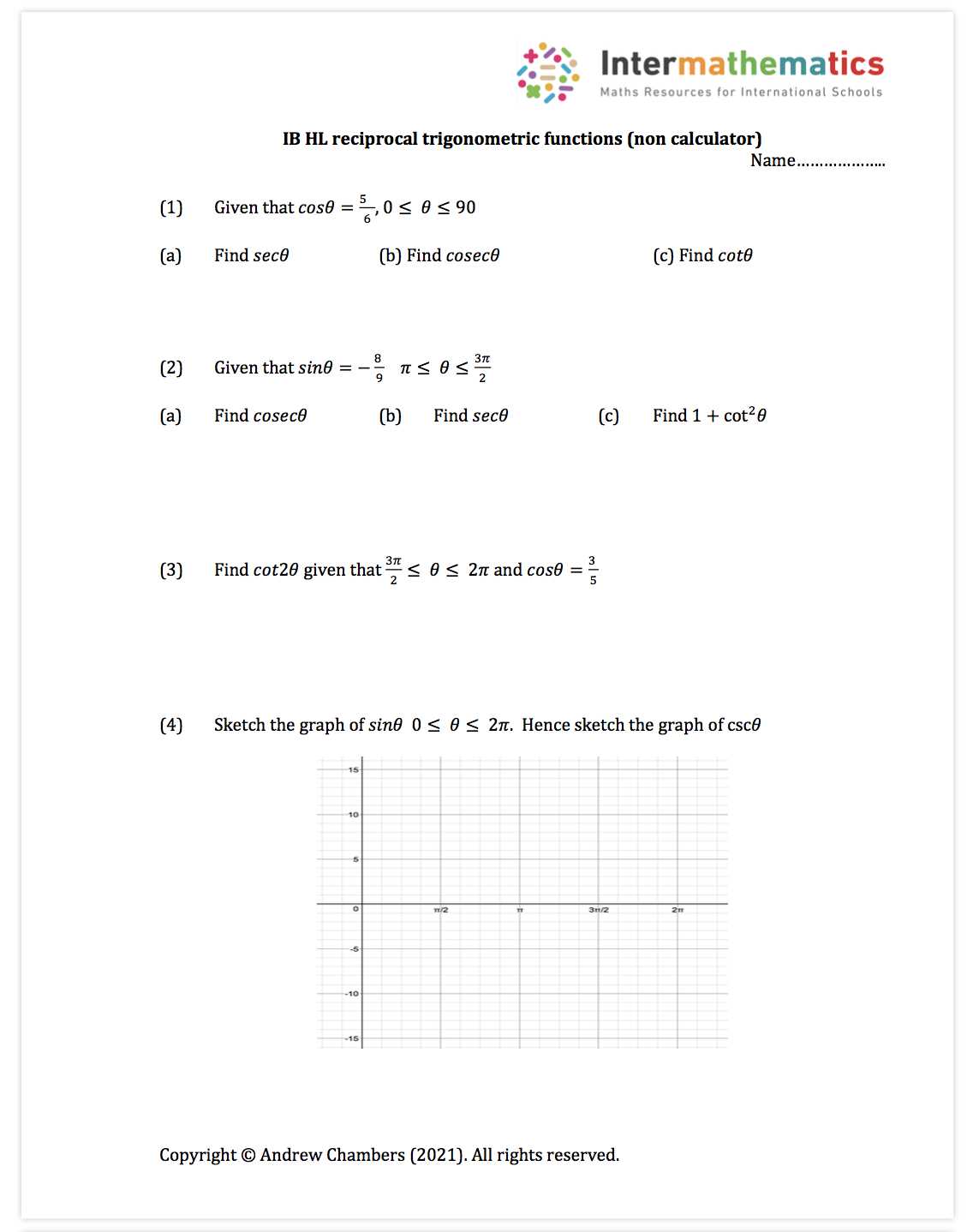
Step-by-step approaches and detailed explanations help in breaking down difficult problems into manageable parts, allowing for clearer insights. By reviewing different methods and practices, learners can develop a stronger grasp of the material and improve their overall performance in solving related exercises.
Whether you are looking to refine your skills or need additional support in understanding difficult topics, this guide offers valuable resources and techniques to guide you through the learning process. Emphasizing clarity and accuracy, it ensures a comprehensive understanding of the most important aspects of the subject.
Cpm Geometry Chapter 10 Answers

This section focuses on solving key mathematical problems and understanding the underlying principles that govern the concepts discussed. By breaking down complex tasks into simpler steps, it provides clear guidance on how to approach each type of problem effectively. The goal is to develop a deep understanding of the methods used and their applications in different scenarios.
Through detailed explanations and step-by-step solutions, this guide helps learners navigate difficult exercises with confidence. Each solution is designed to clarify the reasoning behind each step, making it easier to apply the techniques in future problems. Whether tackling basic challenges or more advanced topics, the emphasis is on mastering the core ideas and improving problem-solving skills.
The provided examples not only showcase various strategies but also highlight common pitfalls and how to avoid them. This approach ensures that learners gain a comprehensive understanding of the material, empowering them to solve similar problems independently in the future.
Understanding Key Concepts of Chapter 10
This section delves into the essential ideas and methods that form the foundation of the material covered. By focusing on critical principles, students can gain a clearer understanding of how to approach a variety of mathematical problems. These concepts are vital for mastering more complex topics and provide the necessary skills to solve increasingly challenging exercises.
Core Principles to Focus On
- Fundamental Theorems: Grasping the key theorems is crucial for building a strong foundation in this area.
- Problem-Solving Strategies: Learning how to break down problems into manageable parts enhances problem-solving skills.
- Practical Applications: Understanding how these principles apply to real-world scenarios strengthens conceptual understanding.
Key Techniques for Mastery
- Logical Reasoning: Developing logical reasoning abilities helps in making connections between different concepts.
- Step-by-Step Solutions: Approaching problems methodically ensures clarity and reduces the risk of errors.
- Practice and Repetition: Consistent practice with a variety of problems is essential for reinforcing learned techniques.
By focusing on these core ideas, learners can enhance their understanding and build the confidence needed to tackle more advanced challenges in the subject. The mastery of these principles sets the stage for continued success and deeper learning.
Step-by-Step Solutions for Geometry Problems
Understanding the approach to solving complex problems begins with breaking them down into smaller, more manageable steps. By following a structured method, learners can effectively address each part of the problem and arrive at a solution with clarity. This step-by-step process not only simplifies the task but also helps in reinforcing key concepts.
The first step is identifying the given information and determining what needs to be found. Once the goal is clear, it’s important to choose the appropriate methods or formulas that apply to the problem at hand. Each stage should be tackled methodically, ensuring that no detail is overlooked.
By carefully following each step, learners develop a deeper understanding of the logical flow required to solve such problems. With practice, this approach builds confidence, allowing students to apply the same strategies to new and more difficult challenges in the future.
Tips for Solving Chapter 10 Exercises
Successfully tackling exercises requires a strategic approach that helps in both understanding the material and applying the right methods. Being organized and methodical is key to working through each problem efficiently. By following a few essential tips, learners can improve their ability to solve even the most challenging tasks.
First, it’s crucial to carefully read the problem and highlight the given information. Once you understand what is being asked, break the problem into smaller parts and tackle each part step by step. This approach helps in avoiding mistakes and ensures that no detail is overlooked.
Additionally, practicing regularly with different types of problems strengthens problem-solving skills. It’s also helpful to revisit previous exercises and solutions to identify patterns or common strategies that can be applied to new problems.
Common Mistakes in Geometry Chapter 10
When solving mathematical problems, it’s easy to fall into certain traps that can lead to incorrect solutions. These mistakes often arise from misinterpreting the problem, overlooking key details, or applying the wrong methods. Recognizing these common errors can help learners avoid them and improve their overall problem-solving approach.
- Overlooking Important Information: Sometimes, crucial details are buried within the problem. Always make sure to read carefully and highlight the given data before proceeding.
- Misapplying Formulas: Using the wrong formula or mixing up similar ones is a frequent error. Double-check the formula you’re applying to ensure it fits the situation.
- Skipping Steps: Rushing through steps can lead to errors. It’s important to follow each step in order and verify your work as you go.
- Ignoring Units of Measurement: Not paying attention to units can cause confusion and mistakes in calculations, particularly when converting or working with different systems.
- Assuming Symmetry: Assuming symmetry or patterns without verifying them can lead to incorrect conclusions. Always check assumptions with careful reasoning.
By being aware of these common mistakes, learners can develop better habits and improve their accuracy when tackling complex exercises.
How to Approach Word Problems
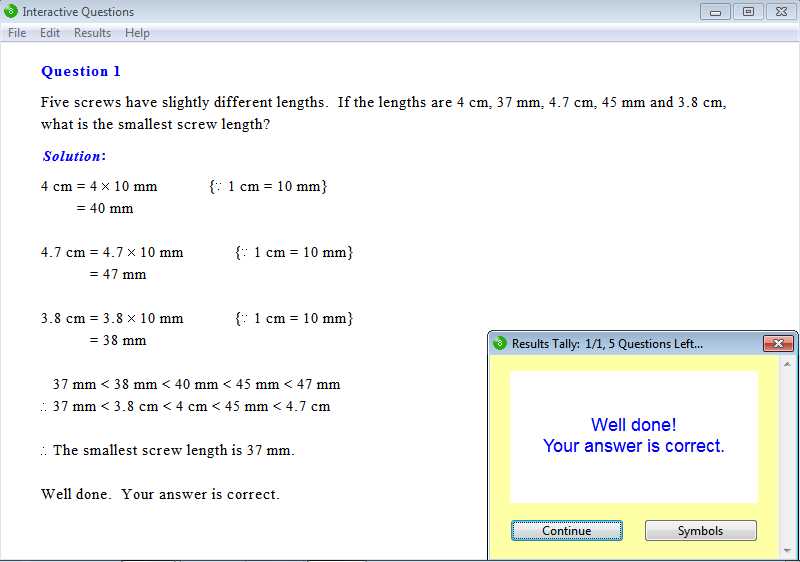
Word problems can often seem daunting due to the mixture of text and mathematical concepts. However, breaking down the problem step by step can make it much easier to understand and solve. The key is to translate the words into a form that makes sense mathematically and to identify the relationships between the various elements involved.
Step 1: Read Carefully and Identify Key Information
Start by reading the problem slowly and carefully. Look for crucial details such as numbers, units of measurement, and any conditions or restrictions. Highlight or underline these pieces of information to keep track of them as you proceed.
Step 2: Plan and Choose the Right Method
Once you understand the problem, decide on the best approach to solve it. This may involve using a specific formula, creating a diagram, or applying logical reasoning. Always choose the method that best fits the situation to avoid unnecessary complexity.
By staying organized and focusing on the relationships between the given information, you can effectively approach word problems with confidence and accuracy.
Overview of Key Theorems in Chapter 10
In this section, we explore the fundamental principles that serve as the backbone for solving many problems. Theorems provide a structured approach to understanding relationships between different elements in mathematics. By mastering these key theorems, students can efficiently tackle a wide range of problems and apply these concepts to more complex situations.
Important Theorems and Their Applications

Each theorem offers specific guidelines or rules for solving problems. These can range from fundamental geometric relationships to more advanced ideas that help in determining distances, angles, and properties of shapes. Understanding how and when to apply these theorems is essential for reaching the correct solution in a systematic manner.
How to Use Theorems Effectively
To make the most of these theorems, it’s important to not only memorize them but also understand their real-world applications. By practicing regularly and incorporating these theorems into problem-solving techniques, learners can develop a deeper understanding of the material and improve their problem-solving skills.
Practice Problems and Their Solutions
Working through practice problems is essential for reinforcing the concepts learned and improving problem-solving skills. By tackling different types of exercises, learners can gain confidence and refine their understanding of the material. This section presents several problems along with their solutions to help solidify the key ideas and methods used in this area of study.
Example Problem 1
This problem involves applying the principles learned to find the unknown values in a given figure. Carefully follow each step to reach the solution.
| Step | Description | Result |
|---|---|---|
| 1 | Identify the given information and the required result. | Identify key variables. |
| 2 | Choose the appropriate formula or method to solve the problem. | Apply the correct formula. |
| 3 | Work through the problem step by step. | Obtain the final answer. |
Example Problem 2
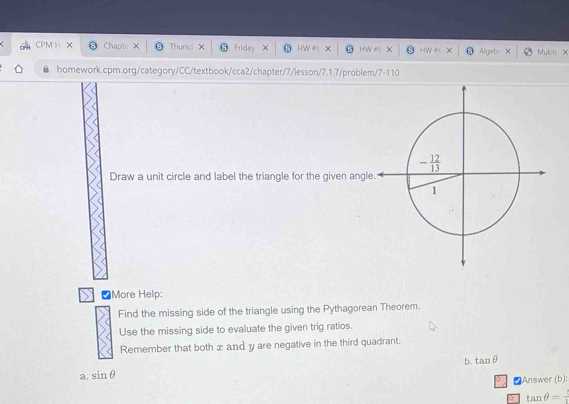
In this problem, we will focus on using logical reasoning to determine the relationship between different parts of a geometric figure. Follow the process closely to understand how to approach similar problems.
| Step | Description | Result |
|---|---|---|
| 1 | Analyze the problem and extract important values. | Note the given numbers and conditions. |
| 2 | Apply relevant theorems or postulates to the situation. | Use geometric properties to make connections. |
| 3 | Perform calculations and find the unknowns. | Arrive at the correct solution. |
By working through these practice problems and reviewing the solutions, learners can better prepare for more advanced exercises and ensure that they have mastered the essential concepts.
Geometry Formulas Covered in Chapter 10

Understanding and applying formulas is crucial when solving mathematical problems, especially when working with geometric figures. Formulas provide the necessary tools to calculate areas, volumes, and other important properties. In this section, we will explore some of the key formulas that are essential for solving problems in this section of study.
Essential Formulas for Two-Dimensional Figures
- Area of a Triangle: A = 1/2 × base × height
- Area of a Rectangle: A = length × width
- Area of a Circle: A = π × radius²
- Perimeter of a Rectangle: P = 2 × (length + width)
- Perimeter of a Square: P = 4 × side
Formulas for Three-Dimensional Figures
- Volume of a Cube: V = side³
- Volume of a Cylinder: V = π × radius² × height
- Surface Area of a Sphere: SA = 4 × π × radius²
- Volume of a Sphere: V = 4/3 × π × radius³
- Surface Area of a Rectangular Prism: SA = 2 × (length × width + length × height + width × height)
By understanding these fundamental formulas, learners will be better equipped to tackle a variety of problems and apply the correct calculations as needed. Mastery of these formulas is a key step in improving problem-solving skills and achieving success in the subject.
Reviewing Geometric Proofs in Chapter 10
In this section, we focus on the process of proving geometric concepts through logical reasoning and established principles. Proofs are essential for demonstrating the truth of various geometric relationships and theorems. By reviewing the steps involved in constructing a proof, students can strengthen their understanding of how to apply theoretical concepts to practical problems.
Understanding the Structure of a Proof
A geometric proof typically follows a structured approach, starting with given information and proceeding through a series of logical steps to reach a conclusion. Each step relies on definitions, postulates, or previously proven theorems. It is essential to clearly explain how each step connects to the next, ensuring that the argument is valid and the conclusion is correct.
Key Strategies for Writing Proofs
- Start with Given Information: Identify what is already known or provided in the problem.
- Use Definitions and Postulates: Apply basic definitions or universally accepted principles to support your argument.
- Consider Different Approaches: If a direct approach seems difficult, consider using indirect methods such as proof by contradiction.
- Keep Your Steps Clear: Avoid skipping steps and ensure each transition is logically sound.
By practicing these techniques and reviewing various proofs, students can build confidence in their ability to construct logical and convincing geometric arguments.
How to Improve Problem-Solving Skills
Enhancing problem-solving abilities is crucial for mastering any mathematical discipline. By developing effective strategies and consistently practicing, individuals can improve their capacity to tackle complex problems with confidence. This section explores key methods that can help sharpen problem-solving skills, enabling learners to approach challenges more efficiently and effectively.
Adopt a Structured Approach

One of the most effective ways to solve problems is by following a clear and organized process. Start by carefully reading the problem to understand what is being asked. Break down the problem into smaller, manageable steps, and identify any known information. Then, select the appropriate methods or formulas and apply them systematically. This structured approach ensures that you stay focused and avoid overlooking key details.
Practice Regularly and Seek Feedback
- Consistent Practice: Regularly working through a variety of problems helps reinforce key concepts and improve your ability to apply them in different scenarios.
- Learn from Mistakes: Reviewing errors and understanding where you went wrong can provide valuable insights into your thought process and guide future improvements.
- Ask for Help: Collaborating with peers or seeking guidance from instructors can offer new perspectives and clarify difficult concepts.
By combining a structured approach with consistent practice and feedback, individuals can gradually improve their problem-solving skills and become more adept at handling even the most challenging tasks.
Real-World Applications of Geometry Concepts
The concepts and principles explored in mathematical studies have far-reaching applications in various industries and everyday life. From architecture to engineering, understanding spatial relationships, shapes, and measurements plays a critical role in designing and creating functional and efficient solutions. This section will explore how these ideas are used in the real world, demonstrating their relevance and importance beyond the classroom.
Applications in Architecture and Construction
Architects and engineers use geometric concepts to design buildings, bridges, and other structures. For instance, understanding the properties of triangles, quadrilaterals, and circles allows professionals to create stable, safe, and visually appealing designs. Measurements such as angles, areas, and volumes are essential for calculating space, determining material requirements, and ensuring structural integrity.
Applications in Technology and Robotics
Geometry is also fundamental in the development of technology, including robotics and computer graphics. In robotics, geometric principles are used to model movement, plan paths, and ensure accuracy in robot design. In computer graphics, understanding the properties of shapes and their transformations helps in creating realistic images and animations.
| Industry | Geometric Concept | Application |
|---|---|---|
| Architecture | Angles, Areas, Volumes | Designing stable structures and optimizing space usage |
| Engineering | Shapes, Symmetry | Creating mechanical parts, ensuring balance and functionality |
| Technology | Coordinate Geometry, Transformations | Designing 3D models, robotics programming |
From the design of everyday objects to the construction of massive infrastructure projects, the applications of geometric principles are vast and diverse. Understanding these real-world connections not only highlights the value of these concepts but also inspires innovative solutions in various fields.
Expert Tips for Geometry Chapter 10
Mastering complex mathematical concepts requires not only understanding the theories but also knowing how to apply them effectively. Whether you’re facing intricate problems or striving to improve your problem-solving techniques, expert advice can make a significant difference in your success. This section offers valuable tips and strategies to help enhance your understanding and boost your performance.
First, it’s important to approach each problem systematically. Break down complex questions into smaller, more manageable steps. Look for key information and identify what is given versus what you need to find. This helps to focus your efforts and prevent confusion, making it easier to navigate through tricky problems.
Another tip is to practice regularly. Mathematics, especially spatial reasoning and measurements, is a skill that improves with consistent practice. By solving a variety of problems, you reinforce your understanding and become more adept at recognizing patterns and using appropriate strategies. It also helps to revisit problems you initially found challenging, as this strengthens your skills over time.
Finally, don’t hesitate to seek help when needed. Consulting with peers, tutors, or instructors can offer fresh perspectives on how to approach problems. Additionally, discussing tricky concepts can lead to better insights and clearer understanding. Collaboration often makes learning more effective and enjoyable.
Resources for Further Geometry Practice
For those looking to deepen their understanding and improve their skills in mathematical concepts, additional resources can provide valuable support. There are a variety of tools, from online platforms to textbooks, that offer exercises, explanations, and interactive lessons. These resources are designed to help reinforce knowledge and challenge students with increasingly complex problems.
Online learning platforms such as Khan Academy, Coursera, and edX offer a wealth of free courses and tutorials. These platforms provide video lessons, step-by-step problem-solving guides, and practice exercises. They also feature interactive quizzes that test your understanding in real-time, making it easier to track your progress and identify areas for improvement.
In addition, textbooks and practice workbooks are excellent sources for structured learning. Many books are dedicated specifically to mastering different aspects of mathematics, offering numerous examples and problems for practice. Some popular titles include “The Art of Problem Solving” and “Math for the Gifted.” These resources typically offer explanations for both basic and advanced topics, catering to learners at all levels.
Lastly, engaging with online math communities or forums, such as Stack Exchange or Reddit’s r/learnmath, can provide an excellent opportunity for peer learning. These communities allow students to ask questions, share insights, and solve problems together. They also offer access to a diverse group of learners, each with unique perspectives that can help clarify difficult topics.
Summary of Important Chapter 10 Topics
In this section, we will review the key concepts and topics covered in the unit, focusing on the most essential principles. Understanding these critical ideas is key to solving a variety of related problems. Below is an overview of the most important subjects to focus on as you progress through the material.
- Understanding Basic Shapes and Properties: Review the properties of common shapes, including triangles, circles, and quadrilaterals. Pay attention to angles, side lengths, and symmetry.
- Angle Relationships: Make sure to understand the relationships between angles, including complementary, supplementary, and vertical angles. These are foundational to many geometric proofs and problem-solving techniques.
- Parallel Lines and Transversals: This topic covers how parallel lines interact with a transversal, creating special angle pairs. Focus on identifying alternate interior angles, corresponding angles, and others.
- Triangle Congruence and Similarity: Learn the conditions for triangles to be congruent or similar, such as side-angle-side (SAS), angle-side-angle (ASA), and others.
- Pythagorean Theorem: Review the theorem and its applications in finding the lengths of sides in right-angled triangles. Be sure to practice solving for unknowns using this theorem.
- Coordinate Geometry: This area introduces the use of coordinates to solve geometric problems. Focus on distance formula, midpoint formula, and the equation of a line.
By focusing on these core topics, you will be well-prepared to tackle a wide range of problems and deepen your understanding of the material. Make sure to practice regularly and apply these concepts to strengthen your problem-solving skills.
How to Prepare for Geometry Assessments
Preparing for a geometry assessment requires a solid understanding of key principles, along with consistent practice. To succeed, focus on mastering the essential concepts, enhancing problem-solving skills, and becoming familiar with common question formats. Here are some strategies to help you effectively prepare and boost your performance.
- Review Key Concepts: Start by revisiting the most important topics, such as properties of shapes, angle relationships, and theorems. Having a strong foundation will make it easier to apply these concepts during the assessment.
- Practice Regularly: Solving a variety of problems helps reinforce what you’ve learned and improves your ability to approach different types of questions. Use practice exercises and past exams to test your skills.
- Understand Theorems and Formulas: Many problems require you to use specific theorems or formulas. Ensure you understand how and when to apply them, and practice using them in different contexts.
- Work on Time Management: During the assessment, time can be a limiting factor. Practice solving problems under timed conditions to improve your speed and accuracy.
- Ask for Help When Needed: If you’re struggling with a particular topic, don’t hesitate to ask your teacher or peers for clarification. Working with others can provide new insights and strengthen your understanding.
By following these strategies and maintaining a consistent study routine, you will be well-prepared to tackle your upcoming assessment with confidence.