
Preparing for the AP exam in statistics can be a challenging yet rewarding experience. Whether you are looking to refine your understanding of key concepts or improve your problem-solving skills, a well-structured approach can make all the difference. In this section, we will focus on practical strategies and essential tips to help you succeed. By examining sample questions and breaking down complex topics, you will gain the confidence to approach your test with ease.
Through detailed explanations and carefully worked-out examples, you will learn how to navigate the most common question types. From understanding data analysis to mastering statistical methods, this guide provides a comprehensive overview that can help boost your performance. Understanding the core principles and applying them to various scenarios is crucial for achieving a high score.
With the right preparation, tackling each section of the exam becomes a manageable task. The key lies in developing a systematic study routine and familiarizing yourself with the various question formats. Whether you are practicing for the first time or looking to improve your existing knowledge, this resource will support you in every step of the way. Consistent practice and review will help you build the expertise needed to excel in your studies and on the test itself.
Preparing for the AP exam in statistics can be a challenging yet rewarding experience. Whether you are looking to refine your understanding of key concepts or improve your problem-solving skills, a well-structured approach can make all the difference. In this section, we will focus on practical strategies and essential tips to help you succeed. By examining sample questions and breaking down complex topics, you will gain the confidence to approach your test with ease.
Through detailed explanations and carefully worked-out examples, you will learn how to navigate the most common question types. From understanding data analysis to mastering statistical methods, this guide provides a comprehensive overview that can help boost your performance. Understanding the core principles and applying them to various scenarios is crucial for achieving a high score.
With the right preparation, tackling each section of the exam becomes a manageable task. The key lies in developing a systematic study routine and familiarizing yourself with the various question formats. Whether you are practicing for the first time or looking to improve your existing knowledge, this resource will support you in every step of the way. Consistent practice and review will help you build the expertise needed to excel in your studies and on the test itself.
Overview of AP Stats Exam Structure
The structure of the Advanced Placement assessment in data analysis and probability is designed to evaluate a wide range of skills and knowledge. The test consists of multiple sections that focus on different types of problems, including data interpretation, statistical modeling, and hypothesis testing. Understanding how the assessment is organized is key to developing a strategic approach to studying and answering the questions effectively.
Multiple-Choice and Free-Response Sections

The assessment is typically divided into two main parts: a multiple-choice section and a free-response section. The multiple-choice questions test your ability to recognize and apply key concepts quickly, while the free-response section evaluates your ability to work through complex problems and explain your reasoning clearly. Each section contributes significantly to the overall score, so balancing preparation for both parts is essential.
Scoring and Time Allocation
The time allocated for each section is carefully structured to allow you to work through the problems at a manageable pace. In the multiple-choice part, speed and accuracy are critical, while in the free-response section, you are expected to demonstrate detailed reasoning and show your steps clearly. Effective time management during the test will help you maximize your score and reduce the chances of rushing through challenging problems.
How to Approach AP Stats Questions
When faced with a set of problems on the test, having a clear and systematic approach is crucial for success. The key to performing well is breaking down each question into manageable parts, understanding what is being asked, and applying the appropriate methods. This section will guide you through strategies to improve your problem-solving skills and ensure that you tackle each challenge efficiently and accurately.
Read and Understand the Question
Before attempting to solve a problem, take a moment to read it carefully. Pay attention to key terms and instructions, as they will guide you in identifying which statistical techniques or formulas to use. Often, the way a question is worded can provide important clues about the best approach to take. Make sure you fully understand the context and what is being asked before moving on to calculations or drawing conclusions.
Organize Your Work and Show Steps
Structure your solutions in a clear and organized manner. Start by writing down any relevant formulas or definitions, followed by the steps you will take to solve the problem. Showing your work not only helps you stay on track but also makes it easier to spot errors if your answer doesn’t match expectations. Clearly presenting your process will also help maximize your score, as some tests reward partial credit for correct methods even if the final answer is wrong.
Key Topics Covered in Exam 1
The first assessment in this subject area covers a range of foundational concepts that are essential for understanding how to analyze and interpret data. The questions focus on various core topics, each designed to test different aspects of your knowledge. A strong grasp of these key areas is crucial for both solving problems accurately and applying the correct techniques to different scenarios.
Fundamental Concepts
Before diving into complex problems, it’s important to be comfortable with the following basic ideas:
- Understanding data types and their classification
- Identifying the appropriate graphs to represent different data sets
- Calculating and interpreting measures of central tendency and variability
Advanced Techniques
As you progress through more challenging problems, these topics will become increasingly relevant:
- Hypothesis testing and p-values
- Linear regression and correlation analysis
- Confidence intervals and margin of error calculations
Familiarity with these areas is vital for solving the problems you will encounter in the first portion of the test. Understanding how to approach each topic will help you tackle questions with confidence and accuracy.
Step-by-Step Solutions for Practice Exam
This section provides a detailed, step-by-step breakdown of how to solve common types of questions found on the test. By following these solutions, you will gain a deeper understanding of how to approach problems systematically, ensuring that you apply the correct methods and arrive at the right conclusions. Each solution highlights the key steps involved in solving the problem and provides explanations for each part of the process.
Solution Process Overview
Each problem is solved using a structured approach that helps ensure clarity and precision. The main steps typically include:
- Identifying the given information and what is being asked
- Selecting the appropriate statistical methods or formulas
- Applying calculations or drawing conclusions based on the data
- Interpreting the results in the context of the problem
Detailed Breakdown of Common Problems

Here are some example problems and how they can be solved step-by-step:
- Problem 1: Calculate the mean and standard deviation for a given data set.
- Step 1: Write down the data set and calculate the mean.
- Step 2: Find the deviation from the mean for each data point.
- Step 3: Square the deviations, sum them up, and divide by the number of data points.
- Problem 2: Interpret the results of a hypothesis test.
- Step 1: State the null and alternative hypotheses.
- Step 2: Determine the test statistic and p-value.
- Step 3: Compare the p-value with the significance level and draw a conclusion.
By practicing these types of problems, you will become more comfortable with the steps involved and be able to approach each question with confidence during the test.
Common Mistakes to Avoid on Exam

When preparing for the test, it’s important to be aware of the common pitfalls that many students fall into. These mistakes can range from simple calculation errors to misinterpreting the problem itself. By understanding and avoiding these errors, you can significantly improve your performance and increase your chances of success.
One of the most frequent mistakes is failing to read the question carefully. Often, students rush through the instructions or overlook key details, leading to incorrect assumptions or misapplied methods. Always take a moment to fully understand what is being asked before jumping into calculations or analysis. Paying attention to small details can make a big difference in the accuracy of your answers.
Another common issue is neglecting to show your work. While it may seem like a time-saver to skip steps, many assessments reward partial credit for correct methodologies. Documenting your thought process clearly not only helps you stay organized but can also earn valuable points, even if your final answer isn’t fully correct.
Additionally, many students struggle with time management during the test. They spend too much time on difficult questions, leaving insufficient time for others. Prioritize your time effectively by tackling easier questions first, ensuring that you don’t get stuck on one challenging problem at the expense of others.
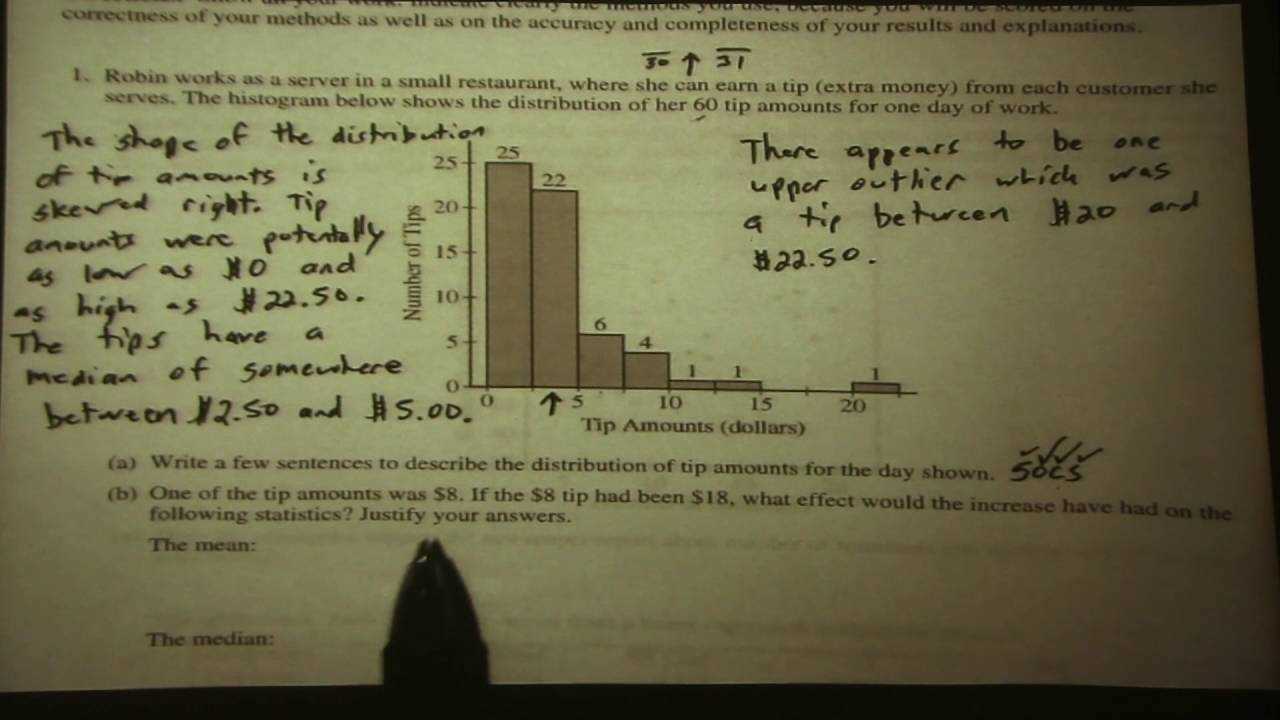
Interpreting Statistical Graphs and Data
Understanding and interpreting visual representations of data is a crucial skill. Graphs and charts are often used to summarize complex information, but interpreting them correctly requires careful attention to detail. In this section, we will discuss how to read and analyze various types of graphical displays and how to extract meaningful insights from the data presented.
Common Types of Graphs
Different types of graphs are used to display different types of data. Here are some common examples:
- Bar charts: Useful for comparing quantities across categories.
- Histograms: Used to show the distribution of a single variable.
- Box plots: Display the spread and central tendency of data, highlighting outliers.
- Scatter plots: Show the relationship between two variables.
Extracting Information from Graphs
When analyzing a graph, always consider the following aspects:
- Title and Labels: Ensure that the graph is labeled correctly and understand what each axis represents.
- Trends and Patterns: Look for any trends, clusters, or outliers that might indicate important insights.
- Context: Understand the context behind the data–what question is the graph answering?
Below is a sample table to practice interpreting statistical data:
| Category | Value |
|---|---|
| A | 25 |
| B | 30 |
| C | 18 |
| D | 22 |
In this table, we can quickly compare the values across categories. Look for the highest and lowest values to identify trends. This type of analysis will help you make informed conclusions based on graphical data.
Strategies for Time Management in AP Stats
Efficient time management is key to performing well under pressure, especially when working through a set of problems in a timed environment. Being able to allocate your time wisely ensures that you can tackle each section effectively, avoid unnecessary stress, and give yourself the best chance to solve all the questions accurately. This section will provide strategies to help you manage your time efficiently during your assessment.
One effective approach is to familiarize yourself with the structure of the test beforehand. Knowing how much time to spend on each section allows you to pace yourself and prioritize questions based on difficulty. It’s important not to get stuck on a single problem for too long. If you find yourself spending excessive time on one question, it’s best to move on and come back to it later.
Another useful technique is to divide your time into blocks. For example, if you have 60 minutes for 20 questions, you might decide to spend 2-3 minutes on each question, leaving a few minutes at the end for review. This structured approach helps prevent rushing through questions or missing critical details due to time constraints.
Lastly, practicing under timed conditions before the actual test is invaluable. Doing so will help you build confidence in your ability to complete questions efficiently while still maintaining accuracy. Regular practice will make you more familiar with the types of problems and increase your comfort level with managing the time available.
Understanding Hypothesis Testing Questions
Hypothesis testing is a fundamental concept used to draw conclusions about a population based on sample data. Understanding how to approach and solve these types of questions is essential for making informed decisions in research or assessments. This section will break down the steps involved in hypothesis testing and provide guidance on how to interpret the results effectively.
Key Steps in Hypothesis Testing
When solving hypothesis testing questions, follow these main steps:
- State the hypotheses: Begin by defining the null hypothesis (H0) and the alternative hypothesis (H1). The null hypothesis typically assumes no effect or no difference, while the alternative hypothesis represents a potential effect or difference.
- Choose the significance level: Determine the alpha level (usually 0.05), which represents the probability of rejecting the null hypothesis when it is actually true.
- Calculate the test statistic: Using the sample data, compute the test statistic that will help you determine whether to reject the null hypothesis.
- Make a decision: Based on the test statistic and the p-value, decide whether to reject or fail to reject the null hypothesis. If the p-value is less than the significance level, reject the null hypothesis.
Example of Hypothesis Testing
Consider the following example:
| Step | Action |
|---|---|
| 1 | State hypotheses: H0: μ = 50, H1: μ ≠ 50 |
| 2 | Choose significance level: α = 0.05 |
| 3 | Calculate test statistic: t = (x̄ – μ) / (s/√n) |
| 4 | Decision: If p-value |
In this example, after calculating the test statistic and p-value, you would compare the p-value to the chosen alpha level. If the p-value is smaller than α, you reject the null hypothesis, suggesting that there is enough evidence to support the alternative hypothesis. If the p-value is larger, you fail to reject the null hypothesis.
Using Calculators Effectively in AP Stats
In assessments involving data analysis, calculators are essential tools for performing complex calculations quickly and accurately. Knowing how to use your calculator efficiently can save you valuable time and reduce the risk of making mistakes during problem-solving. This section will guide you through key features of your calculator that can streamline your process and help you tackle data-related questions with confidence.
Understanding Key Calculator Functions
Modern calculators come equipped with various functions designed to assist with statistical calculations. Some of the most useful features include:
- Data entry: Inputting lists of numbers allows you to calculate important metrics such as the mean, standard deviation, and variance.
- Statistical tests: Many calculators have built-in functions for hypothesis tests, t-tests, chi-square tests, and regression analysis.
- Graphing capabilities: Graphing functions help visualize data distributions, making it easier to identify trends and outliers.
Tips for Efficient Calculator Use
To maximize your calculator’s potential, here are some practical tips:
- Familiarize yourself with your calculator: Practice using its key functions before your test to ensure you’re comfortable navigating through them under time pressure.
- Check your entries: Always double-check your data input to avoid errors in calculations. A small mistake can lead to incorrect results.
- Use the correct modes: Ensure that your calculator is set to the right mode (e.g., statistical or regression mode) to avoid confusion when performing calculations.
By mastering the use of your calculator, you can focus more on interpreting results and applying the correct methods to each problem, rather than being bogged down by manual calculations.
Tips for Answering Probability Questions
Understanding and solving probability questions can be challenging, but with the right strategies, you can approach these problems with confidence. Probability problems often involve calculating the likelihood of certain events occurring, and they require a systematic approach to ensure accuracy. This section will offer useful tips for solving probability-related problems effectively.
Key Strategies for Solving Probability Problems
To successfully answer probability questions, consider the following strategies:
- Define the sample space: Start by clearly identifying the sample space, which represents all possible outcomes of the experiment. This is crucial for calculating probabilities.
- Use basic probability rules: Make sure to apply fundamental principles such as the addition rule for mutually exclusive events and the multiplication rule for independent events.
- Consider conditional probabilities: In some problems, you’ll need to compute the probability of an event occurring given that another event has already occurred. This requires applying conditional probability formulas.
- Visual aids: When possible, draw diagrams such as Venn diagrams or tree diagrams to help visualize the relationships between events. This can simplify complex problems and reduce errors.
Common Mistakes to Avoid
To avoid common pitfalls when solving probability questions, keep these tips in mind:
- Check for independence: Be sure to determine whether events are independent or dependent before using multiplication rules. Incorrect assumptions can lead to wrong answers.
- Watch for overcounting: In cases where multiple events can occur simultaneously, make sure you do not double-count outcomes, especially when applying the addition rule.
- Use correct notation: Always use proper notation when expressing probabilities, such as P(A) for the probability of event A, to avoid confusion.
By following these tips and practicing regularly, you will develop a strong understanding of probability and be better prepared to solve related problems with accuracy and efficiency.
Explaining Confidence Intervals in Detail
Confidence intervals are a critical concept when estimating population parameters based on sample data. They provide a range of values within which the true parameter is likely to fall, offering an indication of the uncertainty associated with a statistical estimate. Understanding how to construct and interpret these intervals is essential for making informed decisions based on data.
What Is a Confidence Interval?
A confidence interval is a range of values, derived from sample data, that is used to estimate a population parameter. The interval has two key components:
- Point estimate: This is the best single estimate of the population parameter, such as the sample mean or proportion.
- Margin of error: The margin of error reflects the variability in the sample estimate and accounts for the uncertainty in predicting the true population value.
The general formula for a confidence interval is:
Point Estimate ± Margin of ErrorInterpreting Confidence Intervals
Once you calculate a confidence interval, it is important to understand its meaning:
- Confidence level: The confidence level, often expressed as a percentage (e.g., 95% or 99%), indicates the likelihood that the interval contains the true population parameter. A 95% confidence level means that if you were to take 100 random samples, approximately 95 of the resulting intervals would contain the true parameter.
- Wider intervals: A wider interval typically indicates a higher level of confidence, as it accommodates more potential values. However, it also means less precision in the estimate.
- Narrower intervals: A narrower interval offers greater precision but reflects less confidence that the true value lies within it.
When interpreting confidence intervals, it’s essential to remember that they do not guarantee that the true population parameter lies within the range for any given sample, but rather they reflect a level of certainty based on the data and the chosen confidence level.
Regression and Correlation on Exam 1
Understanding the relationship between two variables is a crucial aspect of data analysis. Regression and correlation are key techniques used to measure and model these relationships. In this section, we will explore how to apply these methods effectively when analyzing data and how they might be tested in an assessment scenario.
Regression Analysis
Regression analysis helps to model the relationship between two variables by fitting a line or curve to the data points. This method allows us to predict the value of one variable based on the value of another. The most common type of regression is linear regression, which uses a straight line to represent the relationship.
| Term | Explanation |
|---|---|
| Slope | The slope of the regression line indicates how much the dependent variable changes for each unit increase in the independent variable. |
| Intercept | The intercept is the point where the regression line crosses the vertical axis, representing the value of the dependent variable when the independent variable is zero. |
| R-squared | R-squared is a measure of how well the regression line fits the data. A value closer to 1 indicates a better fit, while a value closer to 0 suggests a poor fit. |
Correlation Analysis

Correlation measures the strength and direction of the relationship between two variables. It is represented by the correlation coefficient, often denoted as “r,” which ranges from -1 to +1. A positive correlation means that as one variable increases, the other also increases, while a negative correlation indicates that as one variable increases, the other decreases.
| Correlation Coefficient (r) | Interpretation |
|---|---|
| +1 | Perfect positive correlation; as one variable increases, the other increases in a perfectly linear fashion. |
| 0 | No correlation; there is no linear relationship between the two variables. |
| -1 | Perfect negative correlation; as one variable increases, the other decreases in a perfectly linear fashion. |
Both regression and correlation are valuable tools for understanding and interpreting data, especially when assessing how well two variables relate to each other. It is essential to know how to interpret these methods to avoid making incorrect conclusions based on misleading relationships in the data.
Practice Problems for Exam Readiness
Preparing for an assessment involves more than just reviewing notes–it requires actively engaging with the material through problem-solving. By tackling various challenges, learners can sharpen their skills, deepen their understanding, and identify areas that need further attention. This section will focus on the importance of working through sample problems to build confidence and improve performance on the test.
Sample Problem Set

Here are some practice problems that cover essential concepts commonly tested in assessments. Working through these will help solidify your knowledge and prepare you for similar questions on the actual test.
- Problem 1: Given a set of data points, calculate the mean, median, and standard deviation.
- Problem 2: Determine the correlation coefficient between two variables and interpret its meaning.
- Problem 3: Perform a hypothesis test to determine whether the sample mean significantly differs from a known population mean.
- Problem 4: Analyze a scatter plot and describe the type of relationship (e.g., positive, negative, or no correlation) between the variables.
- Problem 5: Construct a confidence interval for a population proportion based on sample data.
Strategies for Solving Problems
To effectively solve these problems, it’s crucial to follow a structured approach. Here are some tips to help you tackle each challenge:
- Understand the problem: Read the question carefully and make sure you know what is being asked. Identify the key information.
- Plan your approach: Determine which concepts and formulas are relevant to solving the problem.
- Work through the solution: Step-by-step, apply the appropriate methods and check your work as you go.
- Double-check your results: Review your calculations and ensure that your answer makes sense in the context of the problem.
By regularly practicing these types of questions, you’ll improve your ability to approach complex problems and feel more confident when it comes time for the real assessment.
Reviewing AP Stats Formulas and Concepts
Mastering key formulas and concepts is essential for success in any assessment that involves data analysis and interpretation. A solid grasp of these tools not only helps solve problems more efficiently but also deepens your understanding of the underlying principles. This section will review the most important formulas and concepts, offering guidance on how to apply them effectively in various scenarios.
Essential Formulas to Know
Understanding and memorizing the fundamental formulas is crucial for tackling a wide range of problems. Here are some of the most commonly used formulas that should be familiar to any test-taker:
- Mean (Average): The sum of all data points divided by the number of data points.
- Standard Deviation: A measure of how spread out the numbers are in a data set. It is the square root of the variance.
- Confidence Interval: A range of values used to estimate the true population parameter. It is typically calculated using the formula: CI = sample mean ± (critical value) * standard error.
- Linear Regression: The equation for a straight line, typically expressed as y = mx + b, where m is the slope and b is the y-intercept.
- Probability of Events: The likelihood of an event occurring is calculated using the formula: P(A) = Number of favorable outcomes / Total number of outcomes.
Key Concepts and Interpretations
In addition to formulas, it’s important to understand the concepts that underpin them. Here are several key ideas that are central to solving problems and interpreting data correctly:
- Sampling Distribution: The distribution of a sample statistic (such as the sample mean) over many samples drawn from the same population.
- Hypothesis Testing: A method used to test the validity of a claim about a population parameter. It involves setting up null and alternative hypotheses and determining whether to reject or fail to reject the null hypothesis based on sample data.
- Correlation and Causation: While correlation indicates a relationship between two variables, it does not necessarily imply that one variable causes the other. Understanding this distinction is key to correctly interpreting results.
- Significance Level: A threshold used to determine whether the results of a hypothesis test are statistically significant. It is typically set at 0.05, meaning there is a 5% chance of rejecting the null hypothesis when it is actually true.
Reviewing and mastering these formulas and concepts will enhance your ability to approach problems with confidence and accuracy. The next step is to apply them to practice problems and refine your problem-solving techniques.
How to Improve Your AP Stats Score
Improving your performance in any data analysis test requires a combination of strategic studying, effective practice, and strong test-taking skills. By focusing on key areas and mastering essential concepts, you can boost your chances of achieving a higher score. This section provides actionable tips and techniques to help you improve your results and feel more confident during the assessment.
Effective Study Strategies
To make the most of your study time, it’s important to adopt strategies that promote understanding and retention. Consider the following methods:
- Focus on Key Concepts: Prioritize understanding the core principles, such as probability, data interpretation, and hypothesis testing. These concepts often form the foundation of many problems.
- Practice Regularly: Consistent practice helps reinforce what you’ve learned. Use a variety of practice problems to challenge yourself and identify areas where you need more work.
- Use Study Guides: Comprehensive study guides can help you organize your learning. Break down topics into manageable sections and review them systematically.
- Work on Problem-Solving Techniques: Focus not just on memorizing formulas, but also on developing the ability to apply them to real-world scenarios. This will help you approach unfamiliar problems with ease.
Test-Taking Tips
In addition to preparing through study, having a good strategy during the test itself is essential. Here are some helpful test-taking tips:
- Time Management: Divide your time wisely across all sections. Allocate more time to complex problems, but don’t linger too long on any one question.
- Read Questions Carefully: Make sure you fully understand what each question is asking before jumping to a solution. Pay attention to key words such as “mean,” “probability,” or “standard deviation.”
- Check Your Work: If time allows, revisit your answers to catch any errors. A second look may reveal mistakes that are easy to fix.
- Eliminate Clearly Wrong Answers: If you’re unsure about an answer, try eliminating obviously incorrect options to improve your chances of selecting the right one.
By combining effective study strategies with smart test-taking techniques, you can enhance your overall performance and improve your score. The more consistent and focused you are in your preparation, the more confident you’ll feel come test day.
Key Takeaways from Practice Exam 1
Reviewing the results from any assessment can provide valuable insights into your strengths and areas for improvement. The first test in this series is designed to highlight critical concepts and common mistakes, allowing you to refine your understanding. Here are the key lessons learned from the initial test, which can help guide your future study sessions.
Understanding the Main Concepts
The assessment covers a broad range of topics, but some concepts are more frequently tested and deserve special attention. Focus on:
- Data Interpretation: Be able to analyze and draw conclusions from tables, graphs, and other data presentations. This skill is essential for solving many types of questions.
- Hypothesis Testing: Master the steps involved in testing a hypothesis, including understanding how to calculate test statistics and interpret results.
- Probability: A solid grasp of probability theory will help in solving both basic and complex questions involving likelihoods and outcomes.
Common Mistakes and How to Avoid Them
Many students make similar errors during the assessment, and these mistakes can often be avoided with a bit more attention to detail:
- Misreading Questions: Always take the time to read each question carefully, paying attention to keywords like “not” or “except” that can change the meaning.
- Not Showing Work: For problems requiring calculations or reasoning, be sure to show each step. This not only helps you stay organized, but it also maximizes your chances of earning partial credit.
- Rushing Through Calculations: Speed is important, but accuracy is paramount. Don’t rush through calculations, as small errors can lead to incorrect conclusions.
Improvement Areas
After reviewing the results, consider the following areas to focus on for future preparation:
| Topic | Focus Area | Suggested Practice |
|---|---|---|
| Data Analysis | Ability to interpret different types of data sets | Work through additional problems involving tables and graphs |
| Hypothesis Testing | Understanding how to set up and test hypotheses | Practice identifying null and alternative hypotheses, and performing tests |
| Probability | Calculating and understanding probability distributions | Complete exercises that require calculating probabilities for various events |
By focusing on these key takeaways, you can strengthen your knowledge and better prepare for future assessments. It’s important to approach each new concept with a clear understanding of where improvement is needed and to actively practice those areas before the next test.
Next Steps After Completing the Exam
Once you’ve finished an assessment, it’s essential to move beyond just reviewing your scores. The process of self-reflection and further learning can significantly enhance your future performance. Instead of simply moving on, use this time to address any areas of weakness and strengthen your overall understanding. Here are the next steps to consider after completing the test.
1. Review Your Results
Take the time to carefully analyze your responses. Identify the questions you answered incorrectly and try to understand why. Was it a misunderstanding of the concept, a calculation mistake, or perhaps a failure to read the question carefully? Reviewing these errors will help pinpoint areas where you need further study.
2. Fill Knowledge Gaps
If you found certain topics particularly challenging, it’s time to revisit them. Use textbooks, online resources, or ask for help to deepen your understanding. Practicing similar problems will allow you to solidify your knowledge and avoid repeating mistakes in the future.
3. Strengthen Time Management Skills
If you struggled with managing your time effectively during the test, consider practicing under timed conditions. Set a timer when doing practice problems or mock assessments. This will help you become more comfortable working under pressure and ensure you can complete the test within the allotted time.
4. Seek Feedback

If possible, discuss the assessment with a teacher, tutor, or peer. Getting feedback on your performance can offer new insights and strategies for approaching future questions. They might also help clarify concepts that you found difficult.
5. Set New Goals
After analyzing your performance, set clear and specific goals for your next steps. Whether it’s improving on a particular topic or increasing your efficiency, having a target will guide your study sessions and help you stay focused on areas that require improvement.
By taking a thoughtful and strategic approach after completing the assessment, you ensure that each test becomes a valuable tool for growth, not just a reflection of your current abilities. Through continuous reflection and practice, you will be better prepared for future challenges and ultimately achieve your academic goals.