1985 AP Calculus BC Multiple Choice Answer Key

The AP exam in advanced mathematics presents a significant challenge for many students, testing both conceptual understanding and problem-solving skills. The test is designed to assess a student’s ability to apply theoretical knowledge in practical scenarios, making it crucial for learners to be well-prepared. In this article, we will delve into some of the key questions from this challenging assessment and explore the correct methods for solving them.

Understanding the methodology behind the solutions can provide students with the insight needed to tackle similar problems effectively. By reviewing past exam questions and their respective solutions, students can not only identify common patterns but also improve their approach to answering complex problems. The goal is to build a deeper understanding of the mathematical principles at play, ensuring readiness for future exams.

Through detailed explanations and breakdowns, this guide will offer valuable insights into the specific problems tested in the exam, highlighting the most important areas to focus on for optimal performance. Whether you’re preparing for a future test or reviewing past material, mastering these solutions will sharpen your analytical and problem-solving skills, leading to better exam results.

1985 AP Calculus BC Multiple Choice Answers

This section focuses on solving complex problems presented in one of the most challenging assessments for advanced mathematics students. By analyzing specific problems and their corresponding solutions, learners can better understand the principles that underpin these tests. Each problem is a valuable opportunity to deepen your mathematical knowledge, providing insight into the kind of reasoning expected during the exam.

Reviewing the correct solutions to these key questions not only highlights the proper methods but also helps identify common pitfalls. Understanding how to approach each question effectively will allow students to recognize similar problem types and apply the right strategies in future exams. The goal is to master the techniques that lead to accurate and efficient problem solving.

By breaking down the problems step by step, this section offers a clear explanation of how to arrive at the correct results. Through this process, students can gain confidence in their ability to navigate through complex topics, ensuring they are well-prepared to face any similar challenges in subsequent assessments.

Overview of AP Calculus BC Exam

The AP exam for advanced mathematics assesses a student’s ability to solve problems that require both conceptual understanding and technical proficiency. This exam is designed to challenge students with a range of topics that test their mastery of mathematical principles and their application to real-world scenarios. It is divided into two main sections: one focused on solving problems analytically and another on applying these skills to interpret and analyze given data.

The test evaluates a broad array of topics, from foundational concepts in rates of change and accumulation to more complex ideas involving integration and series. Students are required to demonstrate not only their ability to compute solutions but also their capacity to explain their reasoning and justify their answers. The questions range in difficulty, ensuring that every aspect of the subject is thoroughly covered.

For those preparing for the exam, understanding the structure and scope of the test is critical. The best way to approach the assessment is to familiarize oneself with past questions and their solutions, as this provides valuable insight into the types of problems and strategies that are most commonly tested. A solid grasp of both the theory and the application of concepts is essential for achieving success in this challenging exam.

Key Topics Covered in 1985 Exam

The exam evaluates students’ understanding of several critical mathematical concepts, each testing different areas of advanced problem-solving. The focus is on both theoretical understanding and practical application of various topics, designed to measure how well students can manipulate and interpret mathematical structures. From rates of change to advanced integration techniques, this test covers a wide range of skills needed for success in higher-level mathematics.

Fundamentals of Differential Equations

One of the central topics covered in the exam involves solving and understanding differential equations. These equations require students to demonstrate their ability to apply methods for finding solutions to problems that model real-world scenarios, such as population growth or the behavior of physical systems over time. The test requires a deep understanding of how to manipulate variables and apply integration techniques to derive answers.

Series and Convergence

Another major area explored in the assessment involves infinite series and their properties. Students are tested on their ability to determine the convergence or divergence of series, and to apply tests such as the ratio and root tests. Understanding these concepts is critical for solving complex problems involving summations and approximations, which are frequently seen in real-world applications of mathematics.

Importance of Practice with Past Papers

Practicing with previous exam papers is one of the most effective strategies for mastering the material and preparing for future assessments. By reviewing past questions, students become familiar with the format, structure, and level of difficulty they can expect. This practice not only helps to reinforce learning but also builds the confidence needed to tackle the exam under timed conditions.

When revisiting past papers, students can:

• Identify common themes and recurring topics that are frequently tested.
• Familiarize themselves with the types of problems that require specific techniques to solve.
• Learn how to manage time effectively during the exam.
• Enhance their problem-solving speed and accuracy by repeated exposure to different question types.

Moreover, solving old problems allows students to pinpoint areas where they may need further review. It is an invaluable tool for assessing one’s strengths and weaknesses. With consistent practice, students can improve their ability to approach problems strategically and with greater precision.

How to Use Answer Keys Effectively

Answer keys are a powerful resource for reinforcing learning and improving problem-solving skills. However, simply looking at the solutions without understanding the reasoning behind them can limit their effectiveness. To get the most out of answer keys, it is crucial to engage with them actively, using them not only to verify solutions but also to understand the methods and techniques applied to each problem.

Here are some strategies for using answer keys effectively:

• Review the steps, not just the final answer: Focus on understanding the logical progression that leads to the solution, rather than just checking if you got the correct result.
• Identify patterns: Pay attention to recurring techniques or approaches used in different problems. This can help you recognize similar structures in future questions.
• Cross-check your solutions: After attempting a problem, compare your approach and solution with the key. If you made an error, understand why it happened and how to avoid it in the future.
• Analyze the reasoning: Look at the explanations provided, if available, to gain a deeper understanding of the methods applied. This can clarify any uncertainties and fill gaps in your knowledge.
• Test your understanding: After reviewing a solution, try to explain it in your own words or apply the same method to a different problem to ensure that you truly grasp the concepts involved.

By using answer keys in this way, students can improve both their conceptual understanding and their ability to solve problems efficiently. This approach fosters long-term retention and prepares you for similar challenges in future assessments.

Common Mistakes in AP Calculus BC

During an advanced mathematics exam, students often fall into certain traps that can significantly impact their performance. These mistakes are typically related to misunderstanding key concepts, misapplying formulas, or rushing through problems without proper attention to detail. Recognizing and avoiding these common errors can help students perform more confidently and accurately under exam conditions.

Misunderstanding Key Concepts

One of the most frequent errors involves misinterpreting fundamental principles. For example, students may confuse concepts such as instantaneous rates of change with average rates, leading to incorrect calculations. Another common mistake is misunderstanding the conditions under which certain theorems apply, such as the improper use of limits or applying the wrong method for solving integrals. A deep understanding of the theory behind each topic is essential to avoid such mistakes.

Careless Mistakes in Calculation

Another common issue arises from errors in the actual computation process. These include simple arithmetic errors, incorrect sign usage, or overlooking important constants. In more complex problems, students may fail to simplify expressions fully or misapply the order of operations. Such mistakes often occur under time pressure, so it’s important to double-check calculations before finalizing answers.

Strategies for Solving Multiple Choice Questions

Approaching multiple selection questions in an advanced mathematics exam requires a combination of speed, accuracy, and strategic thinking. The key to solving these problems efficiently lies in understanding the question thoroughly, eliminating unlikely options, and using a systematic approach to find the correct solution. With the right strategies, students can improve both their problem-solving skills and their time management during the exam.

Eliminate Clearly Incorrect Options

One of the most effective strategies for solving this type of question is to quickly rule out options that are obviously wrong. This reduces the number of choices you need to consider, increasing your chances of selecting the correct answer. Focus on identifying any answers that contradict fundamental principles or don’t align with the problem’s structure.

Use Logical Reasoning and Estimation

When unsure of the exact solution, estimation can be a helpful tool. Try to approximate the answer by checking the reasonableness of the options based on what you know. For example, if a problem involves large numbers or complex functions, see if the answers fall within an expected range. Logical reasoning can also help to narrow down options by eliminating choices that don’t make sense given the constraints of the problem.

These strategies, when combined with a thorough understanding of the material, can significantly improve your chances of selecting the correct answer quickly and confidently during the exam.

Understanding the 1985 Exam Format

To perform well in any advanced assessment, it is crucial to familiarize oneself with the structure and timing of the test. Knowing the format allows students to effectively allocate their time and approach each section strategically. The exam typically consists of two major parts: a multiple-response section and a free-response section, each designed to test different aspects of mathematical proficiency.

General Overview of Exam Sections

Each section of the exam presents unique challenges and requires a different approach. The first section, usually consisting of multiple problems, demands quick, accurate answers and is designed to test the ability to apply key concepts under time pressure. The second part, focusing on free-response questions, requires students to provide detailed solutions and explanations for more complex problems.

Time Management and Question Distribution

Efficient time management is crucial for success in this type of test. The exam is designed to challenge students’ ability to solve a variety of problems in a limited time, so it’s important to prioritize questions and ensure that each section is completed within the allotted time. Below is a general overview of the exam structure:

Section	Number of Questions	Time Allotted	Type of Problems
First Section	Multiple Problems	50 Minutes	Quick, computational problems
Second Section	Free-Response	90 Minutes	In-depth problems requiring detailed solutions

By understanding the format and structure of the exam, students can tailor their preparation to meet the specific demands of each section, improving their ability to manage time effectively and solve problems with confidence.

Detailed Explanation of Selected Answers

Understanding the reasoning behind correct solutions is essential for mastering any complex mathematical topic. In this section, we will break down the step-by-step processes used to arrive at the correct results for selected problems from the exam. By carefully examining these solutions, students can gain deeper insights into problem-solving techniques and reinforce their understanding of key concepts.

Step-by-Step Breakdown of Problem 1

In this example, the problem involves solving a complex equation involving integration. The first step is to identify the appropriate method for solving the integral. In this case, we use integration by parts to simplify the expression. After applying the necessary formulas and simplifying the result, we reach the correct value. It’s important to note that checking each intermediate step is crucial to ensure accuracy.

Understanding the Key Concepts in Problem 2

This problem tests the student’s ability to solve a differential equation. To find the solution, we first need to recognize the type of equation and apply the correct method, such as separation of variables. After separating the variables, we integrate both sides of the equation, applying the necessary constants. The final solution involves a logical interpretation of the results, which leads to the correct answer. The key to solving this problem lies in recognizing the structure of the equation and applying the correct integration techniques.

By carefully reviewing the steps involved in these selected solutions, students can improve their problem-solving skills and gain confidence in applying the concepts to other similar questions.

Calculus Theorems in 1985 Exam

The exam features several important theorems and principles that form the foundation of advanced mathematical problem-solving. These theorems provide powerful tools for analyzing functions, solving equations, and understanding the behavior of mathematical systems. Understanding how to apply these theorems is crucial for tackling both theoretical and applied questions. Below is a summary of the key theorems often tested in this type of exam.

Theorem	Application	Key Formula
Fundamental Theorem of Calculus	Links differentiation and integration, allowing us to compute definite integrals using antiderivatives.	∫[a,b] f(x) dx = F(b) – F(a), where F'(x) = f(x)
Mean Value Theorem	Helps in finding the average rate of change of a function over an interval, and relates it to the function’s instantaneous rate of change.	f'(c) = (f(b) – f(a)) / (b – a)
Intermediate Value Theorem	Used to prove that a continuous function takes on every value between its minimum and maximum on a given interval.	If f(a) ≤ k ≤ f(b), then there exists some c in [a,b] such that f(c) = k
Rolle’s Theorem	A special case of the Mean Value Theorem where the function values at the endpoints are equal, leading to at least one point where the derivative is zero.	If f(a) = f(b), then there exists at least one c in (a,b) such that f'(c) = 0

These theorems are central to solving many of the problems presented in the exam, as they provide structured ways to approach complex equations and interpret results. Mastery of these concepts will significantly improve a student’s ability to navigate the exam effectively.

Approaching Limits and Derivatives Problems

Limits and derivatives are foundational concepts in advanced mathematics, and solving related problems requires a solid understanding of both the theoretical principles and the practical techniques for their application. When tackling problems involving limits or rates of change, it’s important to systematically break down each problem, using appropriate methods and shortcuts to arrive at the correct solution.

Approaching Limits Problems

When dealing with limits, the key is to understand the behavior of a function as it approaches a specific point. Below are some strategies for solving limit problems:

• Direct Substitution: Always start by trying to directly substitute the value into the function. If the result is finite, that’s your limit.
• Factoring: If direct substitution results in an indeterminate form (like 0/0), factor the numerator and denominator to simplify the expression.
• L’Hopital’s Rule: For indeterminate forms such as 0/0 or ∞/∞, apply L’Hopital’s Rule by differentiating the numerator and denominator separately and then re-evaluating the limit.
• Special Limits: Familiarize yourself with special limits, such as the limit of sin(x)/x as x approaches 0, which equals 1.

Approaching Derivatives Problems

For problems involving derivatives, it’s important to first identify the type of function you’re dealing with and then apply the correct differentiation rules. Here are some key steps to take:

• Power Rule: Use the power rule for functions in the form of x^n. The derivative of x^n is n*x^(n-1).
• Product and Quotient Rules: For functions that are products or quotients of two functions, apply the product rule (d(uv)/dx = u’v + uv’) or quotient rule (d(u/v)/dx = (v*u’ – u*v’)/v^2).
• Chain Rule: For composite functions, use the chain rule to differentiate the outer function and then multiply by the derivative of the inner function.
• Implicit Differentiation: When dealing with equations involving multiple variables, use implicit differentiation to differentiate both sides of the equation with respect to the variable.

By following these strategies and consistently practicing problem-solving techniques, you will become more comfortable and efficient at tackling both limits and derivatives problems on your exam.

Analyzing Integrals and Differential Equations

Integrals and differential equations are essential concepts in advanced mathematics, often requiring careful analysis and methodical approaches. Understanding how to manipulate integrals and solve differential equations is critical for tackling a wide range of problems, from finding areas under curves to modeling real-world phenomena. This section provides strategies for analyzing and solving these types of problems efficiently.

Analyzing and Solving Integrals

Integrals are used to compute areas, volumes, and accumulated quantities. To approach integration problems, it’s important to recognize the type of integral and apply the appropriate method:

• Basic Integration Rules: Start with basic formulas like the power rule for polynomials or the standard integrals for trigonometric functions.
• Substitution Method: For more complex integrals, use substitution to simplify the expression. This is often helpful when the integral involves composite functions.
• Integration by Parts: Use this technique for products of functions, where the integral of a product is simplified by differentiating one factor and integrating the other.
• Partial Fractions: Decompose rational functions into simpler fractions to facilitate integration, especially when dealing with polynomials in the numerator and denominator.
• Numerical Integration: When an integral cannot be solved analytically, approximate methods such as the trapezoidal rule or Simpson’s rule can be used.

Solving Differential Equations

Differential equations describe the relationship between a function and its derivatives. Solving these equations is often the key to understanding dynamic systems. Here are some strategies for solving them:

• Separation of Variables: For simple differential equations, separate the variables and integrate both sides to find the solution.
• Integrating Factor: For linear first-order equations, multiply the equation by an integrating factor to simplify the solution process.
• Homogeneous Equations: For second-order homogeneous equations, look for characteristic equations whose solutions lead to the general solution of the differential equation.
• Numerical Methods: When analytical solutions are difficult to find, use numerical methods like Euler’s method or Runge-Kutta methods for approximate solutions.

By mastering these techniques and understanding when to apply each method, students can effectively approach integrals and differential equations with confidence and precision.

Graphical Interpretation in Calculus BC

Graphical interpretation is a powerful tool in advanced mathematics, enabling students to visualize complex concepts such as rates of change, areas, and the behavior of functions. Understanding how to interpret graphs correctly not only deepens one’s understanding of theoretical principles but also provides practical insights into problem-solving. By analyzing the graphical representations of functions, derivatives, and integrals, students can gain a clearer perspective on their mathematical relationships and applications.

In many cases, graphs can reveal essential information about a function’s behavior, including its increasing or decreasing nature, local maxima and minima, and points of inflection. Visualizing these concepts helps to reinforce the understanding of abstract ideas and supports efficient problem-solving strategies.

For example, the graph of a function can be used to estimate the value of integrals through the area under the curve or to understand the geometric meaning of derivatives as slopes of tangent lines. Additionally, graphical interpretations can help in analyzing the limits of functions as they approach specific points or infinity, providing valuable insights that can inform solution strategies for more complex problems.

Time Management During the Exam

Effective time management is crucial for success in any timed examination, particularly in subjects that require problem-solving and detailed analysis. By allocating sufficient time to each section and maintaining a steady pace throughout the exam, students can ensure that they complete all tasks with accuracy and confidence. Learning how to manage time effectively allows students to avoid rushing through questions and reduce the likelihood of errors.

Here are several strategies for managing time efficiently during the exam:

• Understand the Format: Familiarize yourself with the exam structure before the test day. Knowing how many questions are in each section and their point value will help you plan your time accordingly.
• Start with the Easier Questions: Begin by tackling the questions you find easiest. This boosts your confidence and ensures you secure quick points before moving on to more challenging tasks.
• Time Allocation: Set time limits for each question or section. For example, allocate a specific amount of time to solve each problem, and try to stick to that limit. If you’re spending too long on one question, move on and come back to it later if time allows.
• Keep Track of Time: Regularly check the clock to ensure you’re staying on track. Many exams provide a visible countdown timer, so use it to gauge how much time remains for each section.
• Leave No Question Unanswered: Even if you’re unsure about a question, make an educated guess. There’s usually no penalty for wrong answers, so don’t leave any questions blank.
• Review and Revise: Reserve the last few minutes to review your answers. If possible, double-check calculations, ensure that you’ve answered all parts of each question, and correct any mistakes you may have overlooked.

By employing these time management strategies, you’ll be able to navigate the exam efficiently, ensuring that you allocate sufficient time for each question and make the most of your skills and knowledge under time constraints.

How to Prepare with Answer Keys

Using answer keys as part of your study process can be an effective strategy to reinforce your understanding and identify areas that need improvement. While answer keys provide the correct solutions, the real benefit comes from analyzing how those solutions were reached. By studying the process behind each answer, you can better understand the concepts and techniques required to solve similar problems in the future.

Here are some strategies for preparing with answer keys:

• Understand the Solution Process: Don’t just look at the final answer; take the time to work through the steps leading to the solution. This will help you understand the reasoning and methods used to arrive at the correct result.
• Identify Common Patterns: As you work through multiple problems and their corresponding solutions, look for recurring strategies or techniques. Recognizing patterns will help you solve future problems more quickly and accurately.
• Learn from Mistakes: If you find a mistake in your own work, compare your solution with the correct one to pinpoint where you went wrong. Understanding your errors is a key part of the learning process and will help prevent similar mistakes in the future.
• Practice Similar Problems: Once you’ve reviewed a solution, test your understanding by solving similar problems on your own. Use the answer key to verify your approach, but try to work through the problem independently first.
• Refine Your Techniques: Answer keys can also reveal more efficient methods of solving problems. If a solution uses a technique you didn’t consider, incorporate it into your problem-solving toolkit for future use.

By actively engaging with answer keys in this way, you can turn them into a valuable learning resource, helping you improve your skills and build greater confidence for exams.

Reviewing Commonly Tested Concepts

As you prepare for any advanced exam, it’s important to focus on the core concepts that are frequently tested. These fundamental topics often form the foundation of many problems and can appear in various forms. By reviewing these key areas, you ensure that you are well-equipped to tackle a wide range of questions. In this section, we’ll go over several concepts that are essential for success in advanced mathematics assessments.

Fundamental Theorems and Properties

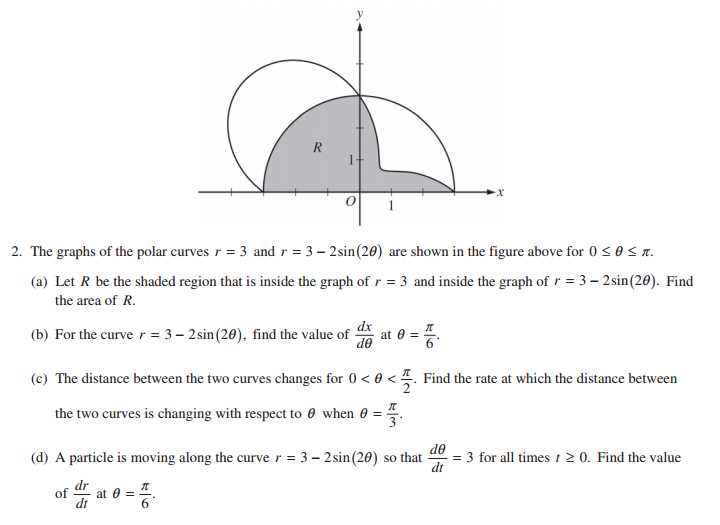
Several theorems and properties are central to solving problems effectively. A solid understanding of these can make it easier to approach complex problems and identify the most efficient methods for solving them. Below is a table summarizing some of the most commonly tested theorems:

Theorem/Property	Description
Fundamental Theorem of Calculus	Connects differentiation and integration, showing that the integral of a function can be reversed by differentiation.
Mean Value Theorem	States that for a continuous function, there exists at least one point where the instantaneous rate of change equals the average rate of change over an interval.
Chain Rule	Allows for the differentiation of composite functions, essential for handling functions of functions.
Integration by Parts	Helps to solve integrals of products of functions, breaking them down into simpler parts.
Power Rule	A basic differentiation rule used to find the derivative of polynomial functions.

Applications of Derivatives and Integrals

Understanding how derivatives and integrals are applied in real-world contexts is crucial for mastering their use. These applications often test your ability to interpret and solve problems based on concepts such as rates of change, optimization, and area calculations. Here are some areas to focus on:

• Related Rates: Problems involving two or more variables changing with respect to time, where the relationship between them must be derived using differentiation.
• Optimization Problems: These problems require you to find maximum or minimum values of functions under certain conditions, often involving setting the derivative equal to zero.
• Area Under Curves: Integral calculations are commonly used to determine the area under curves, representing physical quantities such as distance or total accumulated change.
• Volume of Solids: Use integrals to find the volume of solids of revolution, a fundamental concept in geometry and physics.

By reviewing these essential concepts and practicing with a variety of problems, you’ll be well-prepared to approach any exam with confidence and clarity.

Improving Accuracy on Multiple Choice Tests

Maximizing accuracy in exams is essential for achieving the best possible scores. Success often depends not only on knowledge but also on the ability to apply that knowledge effectively within the constraints of a timed exam. Understanding how to approach questions methodically and avoid common pitfalls can significantly improve performance. This section explores strategies for enhancing precision during test-taking, ensuring that every question is answered as accurately as possible.

Here are key techniques to improve accuracy when answering questions:

• Read Questions Carefully: Always read the question and all options carefully before selecting your answer. Misinterpreting a question can lead to avoidable mistakes.
• Eliminate Clearly Wrong Options: Begin by crossing out answers that are obviously incorrect. This increases the probability of choosing the correct answer by narrowing down your options.
• Double-Check Your Work: If time allows, review your answers to ensure they are consistent with the question’s requirements and check for simple mistakes.
• Use Process of Elimination: For challenging questions, even if unsure, try to reason through the possible answers and eliminate as many wrong choices as possible.
• Manage Time Effectively: Spend an appropriate amount of time on each question, but don’t get stuck on one. Move on if needed and come back later if time permits.
• Stay Calm Under Pressure: Test anxiety can cause errors. Staying calm allows for clearer thinking and helps you avoid rushed or careless mistakes.

Additionally, practicing under timed conditions can help improve both speed and accuracy. Here’s a table of tips to enhance accuracy:

Strategy	Description
Active Reading	Focus on understanding what the question is asking before looking at the options.
Process of Elimination	Cross out obviously wrong options to increase your chances of selecting the right one.
Use Rough Work	Write down key information or calculations to organize your thoughts and avoid mistakes.
Practice Regularly	Taking mock tests can help identify patterns in mistakes and sharpen your ability to spot errors during the actual exam.

By employing these strategies, you can significantly increase your accuracy, leading to better performance on any exam and reducing the risk of unnecessary mistakes.

Additional Resources for AP Calculus BC

Preparing for advanced mathematics exams requires more than just practicing problems; it involves accessing a variety of tools and resources that can deepen your understanding and enhance your problem-solving skills. By leveraging the right materials, you can clarify complex concepts, improve your test-taking strategies, and gain confidence. In this section, we highlight several useful resources that can support your preparation and help you excel in your exam.

Here are some additional materials and platforms that can be invaluable for your studies:

• Online Tutorials and Videos: Websites like Khan Academy, Coursera, and YouTube offer free video tutorials covering essential topics and problem-solving techniques. These can help you understand difficult concepts through visual and step-by-step explanations.
• Practice Tests: Taking practice exams under timed conditions is one of the best ways to familiarize yourself with the test format. Many sites, including AP Central and other educational platforms, provide past papers and mock tests.
• Study Guides and Textbooks: Comprehensive textbooks such as “Stewart’s Calculus” or “Thomas’ Calculus” provide detailed explanations, example problems, and practice exercises. Additionally, study guides specifically designed for the exam can offer targeted review material.
• Mathematical Software: Tools like Wolfram Alpha and GeoGebra can assist in visualizing functions, solving equations, and checking your work. These platforms are excellent for clarifying problems and providing a deeper understanding of mathematical relationships.
• Study Groups: Collaborating with peers can reinforce your learning and expose you to different problem-solving approaches. Join online forums or study groups to discuss concepts and share resources with others preparing for similar exams.
• AP Exam Prep Books: Books like “Barron’s AP Calculus BC” and “Princeton Review AP Calculus BC” offer extensive practice problems, exam strategies, and tips to help you review the material and master the key concepts.

By utilizing a combination of these resources, you can build a well-rounded preparation plan that addresses all aspects of the exam. The more diverse your study materials, the better equipped you’ll be to approach both theoretical and practical problems with confidence and accuracy.