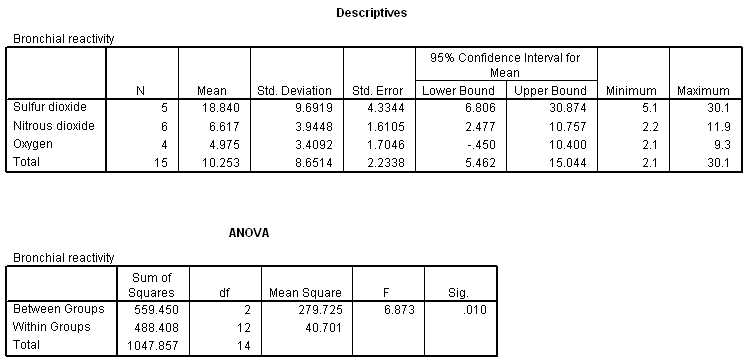
In the field of data analysis, comparing multiple groups or treatments is essential for drawing meaningful conclusions. One of the most effective tools for this purpose is a method that evaluates the differences between group means to determine if they are statistically significant. By practicing various scenarios, learners can enhance their understanding of how to approach such analysis, leading to more accurate interpretations of data.
Understanding how to navigate through this process requires a solid grasp of its underlying concepts. By solving different types of exercises, individuals can strengthen their skills, learn to recognize patterns, and avoid common pitfalls. This not only improves one’s ability to perform statistical tests but also boosts confidence in interpreting complex data results.
Through engaging with a wide range of exercises, learners can refine their techniques and develop a deeper appreciation for the importance of statistical methods in real-world applications. Whether for academic purposes or professional use, mastering this area of study is crucial for those seeking to make data-driven decisions with precision and clarity.
Understanding Anova in Statistics
In statistical analysis, comparing multiple groups to identify differences in their means is essential. This technique is widely used across various fields, from scientific research to business analytics, enabling professionals to assess whether observed variations are due to chance or represent significant findings.
The core idea revolves around examining how variations within groups and between groups contribute to overall data spread. The primary objective is to determine whether the differences between group averages are large enough to conclude that at least one group differs from the others. To achieve this, statistical tests are employed to evaluate these differences in a controlled and systematic manner.
Key steps involved in this approach include:
- Identifying the groups to be compared
- Calculating the variance within each group and between groups
- Performing statistical tests to evaluate the significance of the differences
Understanding how to implement this analysis effectively requires a grasp of various components, including the assumptions underlying these tests and the interpretation of results. Learning how to apply these principles enhances one’s ability to make data-driven decisions and to communicate findings clearly and accurately. Whether you are working with experimental data or observational studies, this technique plays a vital role in drawing reliable conclusions.
Key Concepts in Anova Analysis
To effectively analyze data using a statistical comparison approach, it’s crucial to understand the foundational elements that drive this process. Several key concepts form the basis of this method, and a strong grasp of these ideas will ensure more accurate evaluations of differences between multiple groups. These concepts include variance, hypotheses, and the importance of statistical tests in determining whether observed differences are meaningful.
Among the essential components to consider are the types of variance involved in the analysis. The total variation is split into different sources, and understanding how each contributes to the overall outcome is key. It’s also necessary to evaluate how the observed differences align with expectations under the null hypothesis.
| Concept | Description |
|---|---|
| Between-group variance | Measures how much the group means differ from the overall mean. |
| Within-group variance | Reflects the variation within each individual group. |
| F-ratio | The ratio of between-group variance to within-group variance, used to test significance. |
| Null hypothesis | Assumes no difference between group means, providing a baseline for comparison. |
| Alternative hypothesis | Suggests that at least one group mean is different from the others. |
Once these elements are clearly understood, the next step involves conducting tests to confirm whether the differences found are statistically significant. This ensures that the conclusions drawn are reliable and not the result of random variation.
Types of Anova Tests Explained
When comparing the means of multiple groups, different testing methods are employed depending on the structure of the data and the research question. These statistical approaches allow analysts to evaluate whether observed differences between group averages are significant and not due to random chance. Each type of test has specific applications, assumptions, and requirements that influence how it is used in practice.
The most common types of tests include:
- One-Way Test: Used when comparing the means of three or more independent groups based on a single factor or variable. This test helps determine whether the mean values of the groups differ significantly.
- Two-Way Test: Extends the one-way test by including two factors or variables. This method evaluates the main effects of each factor and also considers the interaction between them.
- Repeated Measures Test: Applied when the same subjects are measured multiple times under different conditions. This test accounts for the correlation between observations from the same subject.
- Multivariate Test: Involves multiple dependent variables and evaluates the relationships between them across different groups. This approach is useful when the research requires a more comprehensive understanding of complex data.
Each of these tests has its own set of assumptions regarding data distribution, sample size, and homogeneity of variance. Knowing when and how to apply each method is crucial for obtaining valid results and drawing accurate conclusions from the data.
Common Mistakes in Anova Calculations
When performing statistical analyses to compare group means, it’s easy to overlook certain aspects that can lead to incorrect conclusions. Missteps in calculations or misinterpretations of results can undermine the validity of the findings. Being aware of common mistakes is crucial for ensuring accurate and reliable results.
Errors in Data Assumptions

One frequent mistake occurs when the assumptions underlying the analysis are not properly checked. Violating assumptions like normality, homogeneity of variances, or independence can distort the test results. Before proceeding with calculations, it is essential to ensure that the data meets the necessary requirements for valid conclusions.
Incorrect Calculation of Variance
Another common error involves miscalculating the variance within and between groups. These calculations are central to evaluating the significance of differences. Mistakes in computing variance, such as ignoring degrees of freedom or misapplying formulas, can lead to incorrect F-ratios and, ultimately, unreliable results.
| Common Mistake | Consequences | Prevention |
|---|---|---|
| Not verifying assumptions (normality, homogeneity) | Leads to inaccurate results and invalid conclusions. | Always check assumptions before performing tests. |
| Errors in variance calculations | Incorrect F-ratio and invalid statistical significance. | Double-check variance and degrees of freedom calculations. |
| Failing to interpret p-value correctly | Can result in false positives or missed significant differences. | Ensure proper understanding of p-value thresholds. |
Being aware of these and other common mistakes helps ensure that statistical analyses are performed correctly and results are interpreted appropriately. Taking the time to verify assumptions, recalculate variances, and correctly interpret significance levels can dramatically improve the reliability of your analysis.
Step-by-Step Guide to Anova Problems
Solving statistical comparison tasks involves a structured approach, ensuring that each step is followed carefully to draw meaningful conclusions from the data. By breaking down the process into manageable steps, you can avoid common errors and confidently interpret the results. This guide provides a systematic method for tackling these analyses, making complex tasks more accessible and understandable.
The first step is to clearly define the hypothesis and the groups being compared. Once the groups are identified, the next step is to collect and organize the data properly. After preparing the data, the calculations for variance and the F-statistic can be performed. Finally, the results need to be interpreted, focusing on the significance level and making decisions based on the p-value.
Here’s a quick overview of the typical procedure:
- Define the null and alternative hypotheses.
- Check assumptions (normality, variance equality).
- Calculate group means and total variance.
- Compute within-group and between-group variances.
- Perform the F-test and obtain the F-ratio.
- Interpret the results using the p-value and critical value.
- Draw conclusions about group differences.
By following this method step-by-step, you can systematically solve and interpret any statistical comparison task, ensuring accurate and reliable results each time.
How to Interpret Anova Results
After performing a statistical comparison between multiple groups, the next critical step is interpreting the results to determine whether there are significant differences between the groups. This involves analyzing several key values, such as the F-ratio, p-value, and degrees of freedom. Properly understanding these results is essential for drawing meaningful conclusions from your analysis.
The first value to consider is the F-ratio, which compares the variation between groups to the variation within groups. A higher F-ratio indicates that the group means are more likely to differ significantly. However, the F-ratio alone is not enough to make a conclusion; it must be evaluated against a critical value, typically derived from an F-distribution table.
Next, the p-value provides the evidence for or against the null hypothesis. If the p-value is less than the chosen significance level (often 0.05), it indicates that the observed differences are statistically significant, and you can reject the null hypothesis. If the p-value is greater than 0.05, the null hypothesis is not rejected, and the group means are considered similar.
- F-ratio: Compare the between-group variance to the within-group variance. A larger value suggests significant differences between groups.
- p-value: Evaluate the strength of the evidence against the null hypothesis. A value below 0.05 typically suggests significant differences.
- Degrees of Freedom: Use the degrees of freedom for both between-group and within-group variances to calculate the F-ratio and interpret the results accurately.
Once you have evaluated these values, you can draw conclusions about whether the observed differences in group means are due to chance or represent a true effect. It is also important to consider any potential errors or biases in your data collection process that could affect the validity of the results.
Different Sources of Variance in Anova

In any statistical comparison, understanding the different sources of variation in the data is essential for determining the underlying causes of observed differences. These variations can stem from multiple factors and are crucial in evaluating the significance of group differences. Identifying and distinguishing between these sources helps to clarify whether the observed variability is due to the treatments being tested or other unrelated factors.
The main sources of variation typically include:
- Between-group variation: This type of variance occurs when the means of different groups being compared differ from one another. It reflects how the treatment or independent variable affects the outcome.
- Within-group variation: This variance arises from differences within each individual group. It reflects natural variation among participants or observations within the same category.
- Residual variation: Often considered the leftover variability that cannot be explained by the model or factors under consideration, residual variance reflects random errors or other unaccounted influences.
By understanding these sources of variance, statisticians can better interpret their results, assess the reliability of their findings, and determine the true effects of the factors being studied. Calculating the proportion of variance attributable to each source also helps in evaluating the overall goodness of fit and statistical significance of the analysis.
One-Way Anova Practice Problem Example
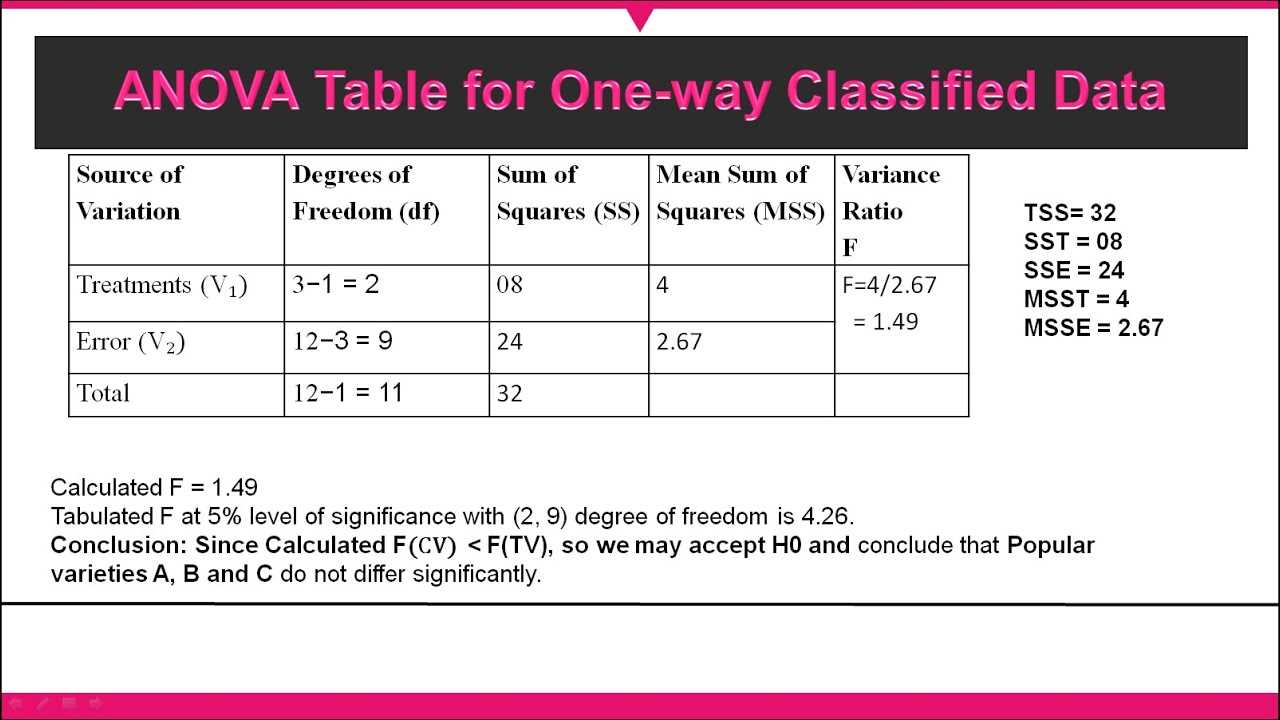
To better understand the process of comparing multiple group means, let’s look at a basic example where three different groups are tested to see if there’s a significant difference between them. This exercise will walk through the key steps of performing a statistical analysis to evaluate group differences.
Imagine a scenario where a researcher is testing the effects of three different fertilizers on plant growth. The three groups are subjected to different treatments, and the researcher measures the growth in centimeters after a specified period. The goal is to determine whether the average growth varies significantly between the groups or if any observed differences could be due to random chance.
Here’s how the data might look:
| Group 1 (Fertilizer A) | Group 2 (Fertilizer B) | Group 3 (Fertilizer C) |
|---|---|---|
| 15, 18, 20, 22, 19 | 16, 17, 19, 21, 23 | 14, 16, 18, 20, 22 |
The steps to analyze this data include:
- Step 1: Calculate the mean for each group.
- Step 2: Compute the overall mean of all observations combined.
- Step 3: Calculate the variance between groups and the variance within each group.
- Step 4: Compute the F-statistic by dividing the between-group variance by the within-group variance.
- Step 5: Compare the calculated F-statistic to the critical value from an F-distribution table to determine statistical significance.
By following these steps, the researcher can assess whether the differences in plant growth between the groups are statistically significant or if the variations are likely due to random fluctuations. This example illustrates the basic process and can be extended to more complex scenarios involving multiple factors or repeated measures.
Two-Way Anova Explained with Examples

When evaluating data involving two independent variables and their interactions, a more complex approach is required to assess how both factors contribute to the outcome. This method allows for the examination of the effect of each independent variable on the dependent variable, as well as how the two factors interact. The ability to analyze these effects simultaneously provides deeper insights into the relationships within the data.
In a typical two-way analysis, there are two independent variables (factors), each with multiple levels, and one dependent variable. The goal is to determine whether the two factors have a main effect on the dependent variable, and if their interaction leads to significant changes in the outcome. For example, you may want to examine how the type of fertilizer and the amount of sunlight affect plant growth.
Consider the following example: a researcher is testing two factors, fertilizer type and watering frequency, on plant growth. The two fertilizers are A and B, and the watering frequencies are 1, 2, and 3 times per week. The plant height is measured at the end of the experiment.
The data might be structured as follows:
| Fertilizer A | Fertilizer B |
|---|---|
| 1 time/week: 15, 18, 20 | 1 time/week: 14, 16, 19 |
| 2 times/week: 20, 23, 25 | 2 times/week: 22, 24, 26 |
| 3 times/week: 25, 28, 30 | 3 times/week: 26, 29, 32 |
To analyze this data, follow these steps:
- Step 1: Calculate the mean height for each combination of fertilizer type and watering frequency.
- Step 2: Determine the main effect of each factor (fertilizer type and watering frequency) by comparing the means within each factor.
- Step 3: Examine the interaction effect by analyzing whether the effect of one factor depends on the level of the other factor.
- Step 4: Perform statistical tests to determine if the main effects and interaction effect are significant.
By interpreting the results of these steps, the researcher can determine how both fertilizer type and watering frequency influence plant growth, as well as whether the combined effect of both factors is greater than their individual effects. This method allows for a more nuanced understanding of how multiple variables work together to influence outcomes.
How to Solve Anova Problems Manually
To perform a detailed analysis of data involving multiple groups, understanding how to solve these calculations by hand is essential for deeper insights into the methodology. This process allows you to break down the components of variance and understand the underlying factors that influence the results. Although modern software tools can simplify these calculations, manual methods provide a stronger grasp of the underlying statistical principles.
Step-by-Step Approach

Follow these steps to manually solve a typical analysis involving multiple groups and a single dependent variable:
- Step 1: Gather the data and organize it by group. Each group represents a different treatment or condition, and you need to ensure that the data is clearly categorized.
- Step 2: Calculate the mean of each group. This is the average of all observations within that group.
- Step 3: Calculate the overall mean, which is the mean of all data points across all groups.
- Step 4: Compute the sum of squares for each group (SSB) and the sum of squares for the error (SSE). These values represent the variation between groups and the variation within groups, respectively.
- Step 5: Calculate the degrees of freedom for both between-group and within-group variations. The degrees of freedom reflect the number of independent pieces of information used in the calculation.
- Step 6: Compute the mean square for between groups (MSB) and mean square for within groups (MSE). This involves dividing the sum of squares by the respective degrees of freedom.
- Step 7: Calculate the F-statistic by dividing MSB by MSE. The F-statistic tells you whether the variability between groups is greater than the variability within groups.
- Step 8: Compare the calculated F-statistic to the critical value from the F-distribution table to determine if the results are statistically significant.
Example
Consider an example where three groups are tested for their average test scores. The data for each group is as follows:
| Group 1 | Group 2 | Group 3 |
|---|---|---|
| 65, 70, 75 | 80, 85, 90 | 55, 60, 65 |
Follow the steps outlined above to compute the sums of squares, mean squares, and the F-statistic. If the F-statistic exceeds the critical value, the conclusion is that at least one of the groups is significantly different from the others.
By carefully following these steps, you can perform a thorough manual analysis and gain a deeper understanding of how the data behaves across different conditions or treatments. The process not only highlights the statistical differences but also strengthens your foundation in statistical reasoning.
Using Anova in Real-World Scenarios
In various fields such as healthcare, marketing, and education, the ability to analyze and compare different groups is crucial for decision-making. By examining the differences in outcomes across multiple groups or conditions, this statistical approach helps in identifying significant patterns, trends, and factors that influence results. Its application is not only limited to experimental designs but extends to real-world problems where multiple variables need to be considered simultaneously.
One common use is in clinical trials, where researchers compare the effects of different treatments on patient outcomes. For example, a study may involve comparing three types of medications to determine which one is most effective in reducing blood pressure. By applying this method, researchers can evaluate whether the differences observed in outcomes are statistically significant or if they occurred by chance.
Another real-world example is in marketing research. Companies often want to test how different promotional strategies impact sales across various regions or demographics. For instance, a retail chain might want to compare the effectiveness of three different advertising campaigns to see which one generates the highest sales. By analyzing the sales data from each group, businesses can make informed decisions about which strategies to invest in moving forward.
Education is another domain where comparing group performance is essential. Schools and universities might compare student scores based on teaching methods, course materials, or class sizes. A school might test whether a new teaching strategy improves student performance compared to traditional methods. Statistical analysis helps educators determine if observed differences in performance are likely to be meaningful or just due to random chance.
In the field of manufacturing, quality control tests often involve comparing products produced under different conditions to assess their consistency. A factory may test how changing one factor, such as machine speed, affects the quality of the product. By analyzing multiple groups of data, managers can determine the optimal conditions for maximum efficiency and quality.
In each of these scenarios, being able to assess the statistical significance of differences between groups is key to making evidence-based decisions. Whether for improving patient outcomes, maximizing marketing ROI, enhancing educational methods, or optimizing production processes, this statistical approach is a valuable tool for understanding complex relationships and guiding effective action.
Understanding F-Statistic in Anova
The F-statistic is a crucial component in assessing the relationship between different groups in a data set. It allows researchers to determine whether the variability between the groups is greater than the variability within the groups. Essentially, it helps in testing whether there are any statistically significant differences between the means of the groups being analyzed.
In a typical analysis, the F-statistic is calculated by dividing the variance between the groups by the variance within the groups. This ratio helps to highlight whether the differences observed between the groups are likely due to a real effect or just random chance. The larger the F-statistic, the more likely it is that the observed differences between groups are meaningful and not the result of natural variability.
The process begins by calculating two types of variance: the between-group variance and the within-group variance. The between-group variance measures how much the group means differ from the overall mean, while the within-group variance measures how much the individual data points within each group vary around their group mean. The F-statistic is the ratio of these two variances.
A high F-statistic indicates that the variability between groups is much larger than the variability within groups, suggesting that the independent variable has a significant effect on the dependent variable. A low F-statistic, on the other hand, suggests that the group differences are small compared to the variation within each group, indicating no significant effect.
After calculating the F-statistic, the next step is to compare it to a critical value from the F-distribution table. This comparison helps determine if the calculated F-statistic is large enough to reject the null hypothesis, which typically states that there are no differences between the groups.
In summary, the F-statistic is a fundamental part of statistical tests, serving as a measure of whether the differences observed in a study are significant. By comparing the variance between and within groups, it helps in drawing conclusions about the effect of different factors on the data. Understanding how to interpret the F-statistic is key to making accurate inferences from data in various fields, from healthcare to business and beyond.
Assumptions Behind Anova Testing

When conducting statistical tests to compare multiple groups, there are certain assumptions that must be met to ensure the validity of the results. These assumptions help ensure that the test produces reliable and meaningful outcomes. If any of these assumptions are violated, the results may be misleading or inaccurate. It’s important to understand these underlying conditions to interpret the findings correctly and make informed decisions based on the data.
One of the key assumptions is that the data in each group are normally distributed. This means that the data points within each group should follow a bell-shaped curve when plotted, indicating that most values cluster around the mean, with fewer values at the extremes. While it’s possible to perform the test even if the data is not perfectly normal, significant deviations from normality may reduce the accuracy of the results.
Another important assumption is the homogeneity of variances, also known as homoscedasticity. This assumption states that the variability or spread of scores within each group should be roughly equal. If the variance between the groups is significantly different, the test may produce biased results. The assumption can be checked using various statistical tests, such as Levene’s test or Bartlett’s test.
Additionally, the observations in each group must be independent of one another. This means that the data points within each group should not influence each other. If the observations are correlated, the test may overestimate the differences between groups, leading to incorrect conclusions.
The table below summarizes the main assumptions behind the statistical test:
| Assumption | Description |
|---|---|
| Normality | Each group’s data should follow a normal distribution (bell-shaped curve). |
| Homogeneity of Variances | The variability within each group should be approximately equal. |
| Independence | The observations within each group should be independent of one another. |
Lastly, it’s important to note that the test assumes that the groups being compared are independent. That is, the grouping factor (e.g., treatment type, condition, etc.) should not have overlapping categories or influence across the groups. Violating this assumption can lead to misleading results and incorrect conclusions about the relationships between the groups.
By ensuring that these assumptions are met, the results of the test will be more reliable, allowing researchers to draw meaningful inferences and make better decisions based on statistical evidence.
Common Errors in Test Assumptions
In statistical testing, ensuring the assumptions are correctly met is critical for the accuracy of the results. However, even experienced analysts sometimes make errors when checking or assuming the necessary conditions. Violating these assumptions can lead to incorrect conclusions and undermine the reliability of the analysis. This section highlights some of the most frequent mistakes made regarding assumptions and how they can be avoided.
Ignoring Normality
One of the most common errors is assuming that the data are normally distributed without performing proper checks. While the central limit theorem suggests that the sample mean will approximate a normal distribution as the sample size increases, this doesn’t mean that the individual data points or small sample sizes will follow a normal distribution. Failing to test normality using statistical tools, like the Shapiro-Wilk test or Q-Q plots, may result in inaccurate interpretations. If normality is violated, alternative statistical methods, such as non-parametric tests, should be considered.
Overlooking Homogeneity of Variances
Another frequent mistake is neglecting the assumption of equal variances across groups. When the variability within each group differs significantly, it can distort the results of the test. This is often overlooked, especially when sample sizes are unequal. To avoid this error, it is important to perform tests like Levene’s test or Bartlett’s test to verify homogeneity. If unequal variances are found, adjustments to the analysis, such as using Welch’s F-test, should be made to account for this issue.
Violation of Independence
Independence between observations is another assumption that can be easily overlooked. In many real-world scenarios, data points may be correlated, such as when measuring repeated observations from the same subjects or when data points share a common cause. In such cases, the violation of this assumption can result in inflated F-statistics, leading to a higher chance of Type I errors. Researchers should take care to ensure that the observations are independent, or use specialized models that account for correlated data, such as mixed-effects models or repeated-measures analysis.
Using Inappropriate Tests for Non-Normal Data
When dealing with non-normal data, some users may apply the standard test without first transforming the data. In these cases, either transforming the data (e.g., log transformation) or using a different statistical method, such as a non-parametric test, can yield more reliable results. Failing to apply the correct approach could lead to invalid inferences.
Understanding and properly addressing these common errors in assumptions will help improve the reliability of the test results, leading to better decision-making and more accurate conclusions in statistical analysis.
Interpreting P-Value in Statistical Testing
The p-value is a fundamental concept in hypothesis testing that helps determine the strength of the evidence against the null hypothesis. By calculating the p-value, researchers can assess whether the observed data is consistent with the null hypothesis or if it suggests a significant difference between groups. Proper interpretation of the p-value is essential for drawing accurate conclusions from statistical tests.
What the P-Value Represents
The p-value measures the probability of obtaining a result at least as extreme as the one observed, assuming the null hypothesis is true. A smaller p-value indicates stronger evidence against the null hypothesis, suggesting that the observed difference is unlikely to have occurred by chance. Here’s a breakdown:
- Low P-Value ( There is strong evidence to reject the null hypothesis, suggesting a statistically significant effect or difference between the groups.
- High P-Value (>= 0.05): There is insufficient evidence to reject the null hypothesis, suggesting no significant effect or difference between the groups.
- Very Low P-Value ( Provides very strong evidence against the null hypothesis, indicating a high level of confidence in the results.
Understanding the Threshold for Significance
In most cases, a significance level (alpha) of 0.05 is used, meaning that if the p-value is less than 0.05, the result is considered statistically significant. However, the threshold for significance can vary depending on the field of study and the nature of the research. In some situations, researchers may use a more stringent threshold, such as 0.01, to reduce the risk of Type I errors (false positives).
Common Misinterpretations
It is important to avoid common misinterpretations of the p-value:
- Not a Measure of Effect Size: A p-value does not indicate the magnitude of the effect, only the likelihood that the result is due to chance. Researchers should also report effect sizes to provide context for the significance.
- Not Proof of the Null Hypothesis: A high p-value does not confirm that the null hypothesis is true. It simply means there is not enough evidence to reject it.
- Does Not Reflect Practical Importance: Even if a result is statistically significant, it may not be of practical or real-world significance. Researchers should consider the practical relevance of the findings.
By properly interpreting the p-value and understanding its context, researchers can make informed decisions based on their data, ensuring the validity and reliability of their conclusions.
Practical Applications of Statistical Analysis
Statistical analysis plays a crucial role in various fields by allowing researchers and professionals to make data-driven decisions. By comparing multiple groups or conditions, this analysis helps determine if there are significant differences between them. Understanding when and how to apply these tests can significantly enhance research outcomes, helping to validate hypotheses and inform future studies.
Applications in Business and Marketing
One of the key areas where this analysis is widely applied is in business and marketing. Companies often use this method to evaluate the effectiveness of different marketing strategies, product features, or customer experiences. For example, a company might compare sales data across different advertising campaigns to determine which one yields the best return on investment.
- Product Testing: Evaluating different versions of a product or service to determine which one performs better in terms of customer satisfaction or sales.
- Customer Segmentation: Analyzing customer behavior based on various demographic or psychographic factors to understand differences in preferences or purchasing patterns.
- Market Research: Comparing the effectiveness of marketing strategies across different geographic regions or target audiences.
Applications in Healthcare and Medicine
In healthcare, statistical analysis helps in comparing different treatment methods, drug efficacy, or patient outcomes. Researchers can evaluate how different groups of patients respond to various therapies, medications, or interventions. For instance, a clinical trial might use this method to assess whether a new drug results in better health outcomes than an existing treatment.
- Clinical Trials: Testing the effectiveness of new treatments or drugs across different groups of patients.
- Health Policy: Comparing health outcomes across different patient demographics to inform policy decisions.
- Epidemiological Studies: Investigating differences in disease prevalence or risk factors across various populations.
Overall, statistical analysis provides valuable insights across numerous sectors, enabling informed decisions that lead to improved practices, products, and services. By identifying patterns and relationships between groups, this approach enhances understanding and promotes innovation in both research and application.
Improving Statistical Problem-Solving Skills
Mastering the art of solving statistical analysis challenges requires a combination of theory, practice, and the application of key techniques. As you work through these exercises, it’s important to focus on improving not only your computational skills but also your understanding of the underlying concepts. This process involves refining your approach to identifying the right statistical tests, interpreting the results correctly, and confidently drawing conclusions from the data.
Key Strategies for Enhancement
Here are a few strategies that can help sharpen your problem-solving abilities:
- Understand the Theory: Having a strong theoretical foundation in statistical concepts allows you to apply the correct methodology in any situation. Make sure you are familiar with concepts such as variance, hypothesis testing, and the interpretation of p-values.
- Work Through Examples: Solving example exercises builds familiarity with the steps involved. Start with simpler cases and gradually tackle more complex scenarios to develop a deeper understanding.
- Practice Data Interpretation: It’s not just about calculations; interpreting data correctly is crucial. Practice reading and analyzing data outputs to identify patterns and relationships.
- Seek Feedback: When possible, ask for feedback on your work. Understanding what went wrong or what could be improved helps to fine-tune your approach.
- Utilize Software Tools: While manual calculations help build foundational knowledge, using statistical software can speed up the process and allow you to focus on analysis and interpretation.
Example: Step-by-Step Approach
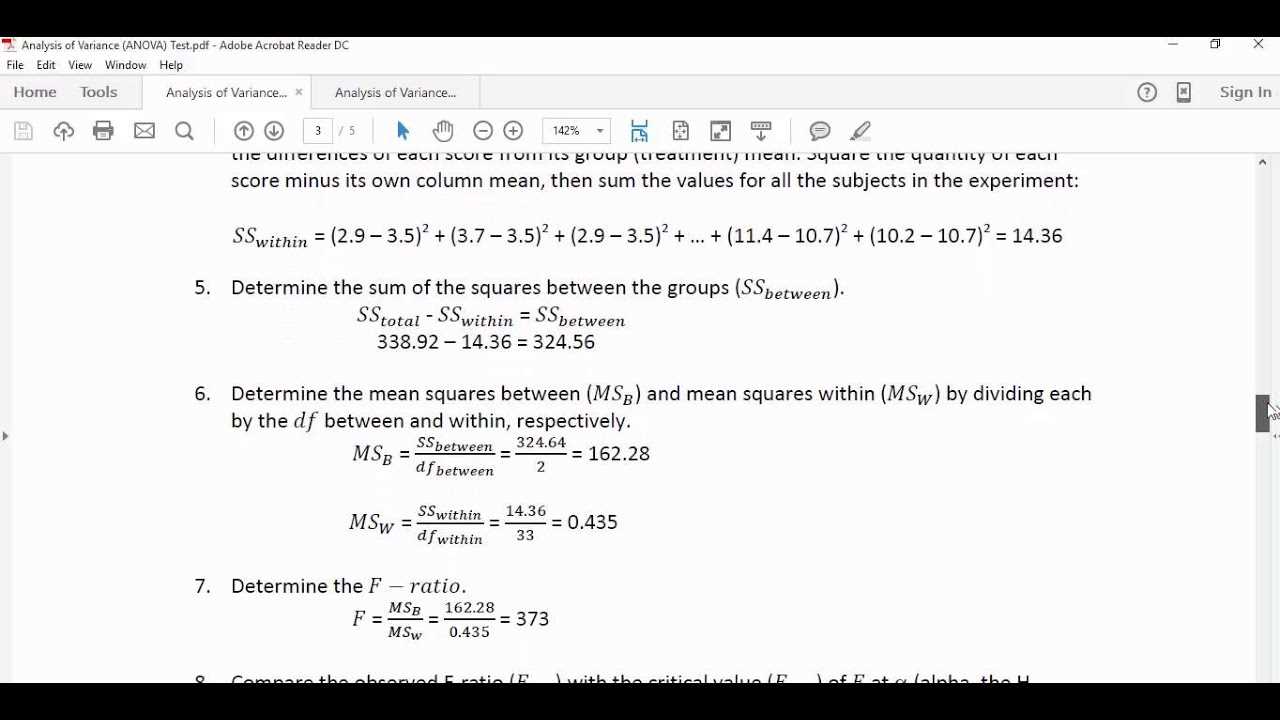
Here’s an example of a typical problem-solving process that you might encounter:
| Step | Action |
|---|---|
| 1 | Define the null and alternative hypotheses based on the research question. |
| 2 | Check assumptions such as normality and homogeneity of variances. |
| 3 | Calculate relevant statistics (e.g., means, variances) for each group. |
| 4 | Compute the test statistic (such as F-statistic) and compare it against critical values. |
| 5 | Interpret the results to make conclusions about the null hypothesis. |
By following a systematic approach and focusing on the key areas listed above, you can steadily improve your statistical problem-solving abilities and approach more complex challenges with confidence.