Success in any standardized exam requires a clear understanding of both the material and the strategies needed to approach it. By focusing on key concepts and practicing effectively, students can improve their performance and tackle challenges confidently. This guide will provide essential insights into preparing for a math exam, covering everything from the most common question types to the best methods for revision.
Effective preparation is the key to achieving your desired score. It’s important to familiarize yourself with the topics that will be tested and hone your skills in solving problems within the given time constraints. Understanding how to approach each question type is just as crucial as knowing the formulas and theories behind them. With the right resources and study techniques, even the most difficult problems can become manageable.
In this article, you will find helpful strategies to enhance your preparation, along with examples of how to tackle problems effectively. Whether you’re looking to practice or improve your problem-solving techniques, this guide offers tools that will help you succeed. From mastering the basics to tackling more complex questions, you’ll be well-equipped to perform at your best.
Geometry Exam Solutions and Guidance

Preparing for any major math exam requires a systematic approach to not only grasp the key principles but also to understand the various problem-solving methods that will be encountered. This section is dedicated to providing comprehensive guidance on how to effectively address the challenges presented in the upcoming test. By exploring different strategies and reviewing potential problem types, students can enhance their ability to achieve a successful outcome.
How to Tackle Common Question Types
When facing a variety of mathematical problems, it’s essential to approach them with the right mindset. Some questions may focus on understanding formulas, while others may require logical reasoning and step-by-step solutions. Developing a strategy for each question type allows for better time management and more accurate responses. Practice with mock questions is an effective way to build familiarity with common formats and to improve the ability to recognize key patterns quickly.
Key Strategies for Efficient Preparation
To maximize performance, students should focus on mastering the fundamental concepts first, ensuring a strong foundation. From there, it’s important to practice solving problems under timed conditions to simulate the actual exam environment. Additionally, reviewing past materials and understanding solution techniques will provide valuable insight into how problems are structured and how to apply the correct approach. Confidence in execution often stems from repeated practice and reflection on areas where improvement is needed.
Understanding the Exam Format and Structure
Familiarizing yourself with the format and structure of any exam is a crucial step toward effective preparation. This section explores the key components of the upcoming test, providing insight into the types of questions you will encounter and the overall design of the assessment. By understanding how the exam is structured, students can focus their preparation on areas that matter most and develop a strategy to approach each section with confidence.
Key Components of the Exam
- Multiple-choice questions: These will test your ability to recall definitions and apply basic principles.
- Constructed response questions: These require a more detailed solution, showing your step-by-step process and reasoning.
- Practical application problems: These will challenge your ability to apply mathematical concepts in real-world contexts.
How to Approach Each Section
- Read the instructions carefully: Understanding what each question is asking is essential for providing the correct response.
- Manage your time: Allocate enough time for each question, focusing on the more complex problems first.
- Review your work: If time permits, always double-check your answers to ensure accuracy.
By recognizing the structure and knowing what to expect, you can tailor your study sessions to improve your efficiency and performance on test day. Mastery of each question type will help ensure you are fully prepared to handle any challenge that comes your way.
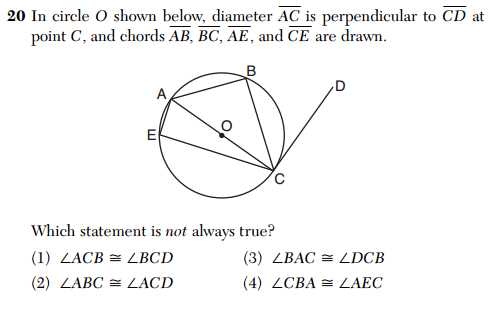
Key Topics Covered in June 2025
Understanding the main subjects of any exam is essential to ensure proper preparation. This section highlights the critical areas that will be tested, helping you focus on the most important concepts. By knowing which topics are likely to appear, you can structure your study plan and practice the right skills to perform your best.
Fundamental Areas to Focus On
- Shapes and Properties: Understanding the characteristics of various figures such as triangles, circles, and quadrilaterals.
- Angles and Their Relationships: Mastery of angles, including complementary, supplementary, and vertical angles.
- Coordinate Geometry: Solving problems involving points, lines, and distances on the coordinate plane.
- Proof and Reasoning: Developing logical arguments to prove geometric theorems and postulates.
Advanced Concepts for Preparation
- Transformations: Learning how to work with translations, rotations, reflections, and dilations.
- Volume and Surface Area: Calculating the surface area and volume of 3D figures such as prisms, spheres, and cones.
- Trigonometry: Applying sine, cosine, and tangent to solve problems related to right-angled triangles.
- Applications of Theorems: Using geometric principles in practical situations and word problems.
By mastering these topics, you’ll have a strong foundation to tackle a wide range of questions effectively. Make sure to review each area thoroughly and practice problems regularly to improve your skills and confidence.
How to Approach Math Exam Questions
Effectively tackling questions in a math exam requires a strategic approach to problem-solving. By breaking down each question into manageable steps and using the right techniques, you can increase your chances of success. This section will guide you on how to approach different types of problems, manage your time efficiently, and ensure that you provide well-structured solutions.
Steps to Follow for Each Question
When you encounter a question, it’s essential to approach it methodically. Here are the key steps to follow:
| Step | Action |
|---|---|
| 1 | Read the question carefully and identify the key information. |
| 2 | Underline or highlight important details, such as numbers and geometric properties. |
| 3 | Visualize the problem by drawing diagrams or creating models if needed. |
| 4 | Decide on the appropriate formula or method to use. |
| 5 | Execute the solution, showing all steps clearly. |
| 6 | Double-check your work for errors, especially with calculations. |
Effective Strategies for Time Management
Time management is critical during a timed exam. Allocate enough time for each question, focusing on easier problems first to secure quick points. For more complex problems, spend additional time, but avoid getting stuck on one question for too long. Use the remaining time to review your answers and make sure your solutions are complete and accurate.
By following these steps and managing your time effectively, you’ll be better prepared to tackle any math exam question with confidence and clarity.
Important Formulas for Math Exam
Mastering key formulas is essential for success in any mathematical test. These formulas provide the foundation for solving problems related to shapes, measurements, and calculations. In this section, we will cover the most important equations you need to know to tackle a variety of questions and improve your problem-solving skills.
Basic Formulas for Shapes and Figures
- Area of a Triangle: Area = 1/2 × base × height
- Area of a Rectangle: Area = length × width
- Area of a Circle: Area = π × radius²
- Perimeter of a Rectangle: Perimeter = 2 × (length + width)
- Perimeter of a Triangle: Perimeter = sum of all sides
Volume and Surface Area Formulas
- Volume of a Rectangular Prism: Volume = length × width × height
- Surface Area of a Cube: Surface Area = 6 × side²
- Volume of a Cylinder: Volume = π × radius² × height
- Surface Area of a Sphere: Surface Area = 4 × π × radius²
These formulas are just a few of the essential equations you’ll encounter on the exam. Make sure to memorize and understand how to apply them, as they will be used in a variety of questions. Being able to quickly recall these formulas will help you solve problems efficiently and accurately under time pressure.
Tips for Effective Time Management
Managing your time effectively during an exam is crucial to ensure that you can answer all questions and still have time to review your work. Proper time management allows you to focus on the most important problems, avoid rushing, and maintain a steady pace throughout the test. In this section, we will discuss strategies to help you allocate time wisely and perform at your best under time constraints.
Key Time Management Strategies
| Strategy | Description |
|---|---|
| Prioritize Easier Questions | Start with questions you find easiest to build confidence and secure quick points. |
| Allocate Time for Each Section | Divide your total time based on the number of questions or sections to avoid spending too long on any one part. |
| Set Time Limits per Question | Estimate how long you should spend on each question, ensuring that you have enough time for all questions. |
| Avoid Getting Stuck | If a question is taking too long, move on and come back to it later if time allows. |
| Use Spare Time for Review | Always reserve some time at the end to check your answers for any errors or missed steps. |
Time Management During Practice
Practice solving problems under timed conditions to develop a sense of pacing. The more you practice, the better you will get at recognizing how much time to spend on different types of questions. Simulating exam conditions will help you manage your time more effectively during the actual test.
By implementing these strategies, you can approach your exam with confidence, ensuring that you have enough time to answer each question thoroughly and review your work for any possible mistakes.
Practice Problems for Better Preparation
One of the most effective ways to prepare for any exam is through consistent practice. By solving a variety of problems, you strengthen your understanding of key concepts and improve your ability to apply them under exam conditions. In this section, we will explore several practice problems designed to test your skills and enhance your readiness for the test.
Practicing problems not only helps you recall formulas and methods but also builds your confidence in solving questions efficiently. The more you practice, the more familiar you become with the types of challenges you may face during the exam.
Problem 1: Solving for Area
Question: A triangle has a base of 8 cm and a height of 5 cm. What is the area of the triangle?
Solution: Use the formula for the area of a triangle: Area = 1/2 × base × height. Plugging in the values, you get:
Area = 1/2 × 8 cm × 5 cm = 20 cm²
Problem 2: Working with Angles
Question: Two angles are supplementary, and one of them measures 65°. What is the measure of the other angle?
Solution: Since supplementary angles add up to 180°, subtract the given angle from 180°:
180° – 65° = 115°
The measure of the other angle is 115°.
Problem 3: Volume of a Cylinder
Question: A cylinder has a radius of 4 cm and a height of 10 cm. What is the volume of the cylinder?
Solution: Use the formula for the volume of a cylinder: Volume = π × radius² × height. Substituting the values, you get:
Volume = π × (4 cm)² × 10 cm ≈ 3.14 × 16 cm² × 10 cm = 502.4 cm³
Problem 4: Perimeter of a Rectangle
Question: A rectangle has a length of 12 cm and a width of 7 cm. What is the perimeter of the rectangle?
Solution: Use the formula for the perimeter of a rectangle: Perimeter = 2 × (length + width). Substituting the values, you get:
Perimeter = 2 × (12 cm + 7 cm) = 2 × 19 cm = 38 cm
These problems cover basic principles that are often tested in exams. By practicing such questions regularly, you will develop a deeper understanding of the material and increase your chances of performing well on the test.
Common Mistakes to Avoid in Math Exams
When preparing for a math exam, avoiding common pitfalls can significantly improve your performance. Many students make simple yet costly mistakes that can easily be prevented with attention to detail and a clear understanding of the concepts. In this section, we will highlight some of the most frequent errors and provide tips on how to avoid them.
Frequent Errors to Watch Out For
- Misunderstanding Question Instructions: Failing to read the question carefully can lead to solving the wrong problem or overlooking important details. Always make sure you understand what the question is asking before proceeding.
- Skipping Steps in Calculations: Skipping intermediate steps in your calculations can lead to errors. Always show your work clearly to help catch any mistakes along the way.
- Incorrect Use of Formulas: Using the wrong formula or misapplying it is a common mistake. Ensure that you are using the correct equation for the given problem and understand how to apply it properly.
- Overlooking Units: Forgetting to include units in your answers, especially for measurements or areas, can result in losing valuable points. Always double-check that you have included the correct units in your final answers.
- Rushing Through the Exam: Trying to finish quickly can lead to careless mistakes. Take your time to read through each problem thoroughly and check your work if time allows.
How to Minimize Errors
- Practice Regularly: Regular practice helps you become more familiar with problem types and formulas, reducing the likelihood of errors during the exam.
- Review Key Concepts: Spend time reviewing essential concepts before the exam to ensure you understand the material and can apply it correctly under pressure.
- Take Your Time: Plan your time wisely during the exam, ensuring that you can give each question the attention it deserves without rushing.
- Double-Check Your Work: If time permits, always go over your answers and check your calculations to catch any mistakes before submitting your exam.
By being mindful of these common mistakes and taking steps to avoid them, you can increase your chances of performing well on your test. Confidence, preparation, and careful attention to detail will help you tackle even the most challenging questions with ease.
How to Use Past Exam Papers
Reviewing past exam papers is an excellent way to prepare for your upcoming test. By practicing with previous papers, you can familiarize yourself with the structure of the exam, the types of questions that are likely to appear, and the level of difficulty. In this section, we will discuss effective strategies for using past exams as a study tool to maximize your preparation and improve your performance.
Benefits of Practicing with Past Papers
Using past exam papers provides several advantages, including:
- Familiarization with Question Format: Past exams often repeat similar types of questions, so practicing with them helps you become accustomed to the format and wording of the questions.
- Identifying Key Topics: By reviewing the range of topics covered in previous exams, you can identify which concepts are frequently tested and prioritize them during your study sessions.
- Time Management Practice: Working through past papers under timed conditions helps you practice pacing yourself and ensures that you can complete the exam within the allotted time.
- Building Confidence: As you solve more practice problems, you will gain confidence in your ability to tackle similar questions on the real exam.
Strategies for Using Past Papers Effectively
While practicing past exam papers, it’s important to approach them strategically. Here are some tips to help you make the most of your study time:
| Strategy | Description |
|---|---|
| Start with Old Papers | Begin by working through exams from previous years to familiarize yourself with the test structure and common topics. |
| Time Yourself | Complete practice papers under timed conditions to develop a sense of the time you need for each section. |
| Review Mistakes | After completing a paper, carefully go over your mistakes and understand why the correct answers are what they are. This will help reinforce your learning. |
| Use Answer Keys | If available, refer to answer keys to check your work and gain insight into how to approach similar problems on the real exam. |
| Focus on Weak Areas | If certain topics or question types consistently trip you up, spend extra time reviewing those areas to strengthen your skills. |
By integrating past exam papers into your study routine, you can significantly improve your test-taking strategies, boost your confidence, and enhance your chances of success. Consistent practice, combined with a thoughtful review of your mistakes, will prepare you thoroughly for the upcoming exam.
Effective Exam Answer Strategies
When approaching any exam, having a clear strategy for answering questions is crucial. A well-thought-out approach helps you maximize your score, manage your time efficiently, and reduce the likelihood of errors. In this section, we will explore key strategies for answering questions effectively, ensuring that you tackle the exam with confidence and clarity.
| Strategy | Description |
|---|---|
| Read Questions Carefully | Always read each question thoroughly to ensure that you understand exactly what is being asked before starting your solution. Pay close attention to keywords and any specific instructions. |
| Plan Your Time | Allocate a set amount of time to each question based on its difficulty. Avoid spending too much time on any single question, and move on if you get stuck. |
| Start with Easy Questions | Begin with questions that you find easier or more familiar. This will help you build momentum and boost your confidence for the more challenging problems. |
| Show Your Work | Always show the steps you take to solve a problem, even if you’re confident in your answer. This can help you recover partial credit in case of mistakes. |
| Use Elimination Techniques | If you are unsure of an answer, use elimination methods to narrow down your choices. Cross out obviously incorrect options and make an educated guess. |
| Double-Check Your Answers | If time permits, go back and review your answers. Check for calculation errors, missed details, or incorrect units that may have been overlooked during your first pass. |
By adopting these strategies, you can approach the exam methodically and ensure that each question is answered as accurately as possible. Preparing in advance and practicing these techniques will allow you to manage both time and stress, setting you up for success on exam day.
Understanding Geometry Problem Types
Every exam features a variety of problem types, each requiring different approaches and strategies to solve. Knowing what to expect and how to tackle each type can greatly improve your efficiency and accuracy during the test. This section will help you identify common problem types, understand their characteristics, and learn how to approach them effectively.
There are typically several categories of problems that you will encounter. Some problems might focus on applying formulas, while others require logical reasoning or visualization. Understanding the structure of these problems is essential for managing your time and responding to questions with confidence.
Here are some common types of problems you may face:
- Multiple Choice Questions: These questions present a set of possible answers, with one or more correct options. You need to quickly analyze the problem and eliminate incorrect choices.
- Constructive Response Questions: These require you to provide a detailed solution, often showing steps and justifications for your reasoning.
- Proof Problems: These questions ask you to demonstrate the validity of a statement through a series of logical steps, often using previously learned theorems or postulates.
- Word Problems: These problems describe a real-world scenario and require you to apply mathematical concepts to solve them. Be sure to carefully translate the text into mathematical language.
- Diagram-Based Problems: These questions include geometric figures, and you must use these visuals to derive solutions. Attention to detail in labeling and measurements is key here.
Familiarity with these types of problems allows you to adopt the best approach for each, whether it’s applying a formula, drawing a diagram, or using logical reasoning. With practice, you’ll become more adept at quickly identifying the type of problem and choosing the most effective strategy for solving it.
Grading System Explained
Understanding how your performance is evaluated during an exam is essential for effective preparation. Each exam typically follows a structured grading system that assigns points based on how well you address the required tasks in each question. This system determines the weight of each section and the overall score you achieve. In this section, we will break down how the grading process works and how it impacts your final result.
The grading is often divided into multiple components, with specific points awarded for different types of responses. Here’s an overview of how points are typically distributed:
- Multiple Choice Questions: These questions usually contribute to a significant portion of the exam score. Each correct answer is typically awarded one point, but the exact value may vary depending on the exam structure.
- Constructed Response Questions: These questions require you to show detailed steps and reasoning. They are often weighted higher because they test both understanding and application of concepts. Points are awarded based on the completeness and accuracy of your work.
- Proof and Justification Questions: These require logical reasoning and the demonstration of mathematical principles. In most cases, partial credit can be given if you provide correct intermediate steps, even if the final answer is incorrect.
- Diagram-Based Questions: Points are given for accurately interpreting the diagram and applying the correct methods to solve the problem. The clarity of your work and the precision of your answers are important in this section.
Typically, exams are scored on a point scale, with higher points indicating a more thorough understanding of the material. Additionally, exams may have a set percentage of questions that focus on core concepts, while others test more complex applications. Understanding this breakdown allows you to focus your studies on both foundational knowledge and advanced problem-solving techniques.
Be sure to check the scoring guidelines provided by the exam board, as each exam may vary slightly in terms of scoring rules and point distribution. Familiarizing yourself with these details will help you prioritize areas of study and manage your time effectively during the exam.
Breaking Down the June 2025 Exam Format
Understanding the structure of an exam is crucial for effective preparation. Knowing how the test is organized, what types of questions to expect, and how much time you have for each section will allow you to plan your approach and manage your time effectively. This section provides a detailed breakdown of the format you can expect in the upcoming exam.
Sections of the Exam
The exam is typically divided into several sections, each testing different aspects of your knowledge and skills. The breakdown is as follows:
- Multiple Choice Section: This section contains a set of questions where you must choose the correct answer from several options. It usually covers a broad range of topics and tests your ability to quickly identify solutions to problems.
- Constructive Response Section: These questions require you to show your work and explain your reasoning. You may need to provide detailed steps for solving problems, which can include drawing diagrams or using specific formulas.
- Proof-Based Questions: These questions assess your ability to logically prove a given statement or theorem. They typically involve writing a series of logical steps and referencing mathematical concepts you’ve studied.
- Application-Based Problems: These questions ask you to apply your knowledge to real-world situations. They may include word problems or require you to interpret visual data, such as graphs or diagrams.
Time Allocation and Strategy
Time management is a key factor in successfully completing the exam. Here’s an overview of how to allocate your time across the different sections:
- Multiple Choice: Typically, you will have a limited amount of time for this section, as it consists of quick-answer questions. Focus on speed and accuracy, but don’t spend too much time on any one question.
- Constructive Response: These questions require more time and attention to detail. Be sure to allocate enough time to show your work clearly and thoroughly.
- Proof and Application Questions: These are often the most time-consuming. Make sure you fully understand each step of the process before starting, and try to leave enough time to review your work.
By breaking down the exam format into its components, you can better understand how to approach each section and make the most of your study time. The key is to familiarize yourself with the types of questions, practice problem-solving, and build confidence in your ability to manage time during the test.
What to Expect on the Day of the Exam
The day of the exam can be both exciting and nerve-wracking. Understanding what to expect beforehand can help alleviate anxiety and ensure that you are fully prepared. On the day of the test, you’ll be expected to follow specific procedures, adhere to guidelines, and stay focused on performing your best. This section will walk you through what to anticipate so you can feel confident and organized when the big day arrives.
Before the exam begins, make sure to arrive early at the test center. This gives you time to settle in, check in, and get comfortable with the surroundings. You will be asked to show a valid ID, and in some cases, your registration confirmation. Be sure to bring the necessary materials such as pens, pencils, and an eraser. Some exams may also allow or require a calculator, so make sure to check the requirements ahead of time.
Once you are seated, the proctor will explain the exam procedures, including time limits, rules, and how to handle any issues that may arise during the test. Pay close attention to these instructions, as they are important for ensuring that you understand the format and expectations of the exam.
During the exam, stay calm and focused. Use the time efficiently by moving through questions methodically. Remember, if you encounter a challenging question, it is okay to move on and come back to it later. If you finish early, take time to review your work to ensure you didn’t overlook any details.
Once the test is complete, you will be instructed on how to submit your work. Stay organized throughout the entire process to avoid any last-minute confusion. Afterward, relax and celebrate the fact that you’ve completed your preparations and put in the hard work to succeed.
Resources for Additional Geometry Practice
To further strengthen your skills and improve your understanding of key concepts, there are numerous resources available that can provide additional practice. Whether you’re looking for online tools, textbooks, or interactive exercises, the right materials can help you reinforce what you’ve learned and tackle more complex problems with confidence. Below are some recommended options for practicing and deepening your knowledge.
Online Platforms
There are several websites and platforms that offer a wide range of practice problems, tutorials, and video lessons. These resources can help you get a hands-on approach to solving problems and understanding different concepts.
- Khan Academy: Offers free video lessons and practice exercises for all skill levels. You can learn and practice at your own pace.
- IXL: Provides personalized practice that adapts to your strengths and weaknesses. It offers a comprehensive set of practice questions for all topics.
- Brilliant.org: An interactive learning platform that helps develop problem-solving skills through fun and engaging challenges.
Textbooks and Workbooks
Traditional textbooks and workbooks remain valuable resources for structured learning. These often include detailed explanations and a wide variety of practice questions to test your knowledge.
- Scholastic Math Workbooks: These books cover a wide range of topics with clear explanations and exercises to practice.
- McGraw-Hill Education: Offers comprehensive textbooks with step-by-step solutions and additional practice problems.
Study Groups and Forums
Sometimes, collaborating with others can help clarify concepts and make studying more interactive. Joining a study group or participating in online forums can offer support and additional resources for practice.
- Reddit (MathHelp and StudyGroups): Online communities where students share study tips, ask questions, and offer advice.
- Discord Study Groups: Many Discord servers are dedicated to collaborative studying, where you can ask questions and work through problems with others.
Incorporating these resources into your study routine will help you stay engaged, overcome difficulties, and improve your performance over time. Consistent practice is the key to mastering any subject, so take advantage of these tools and challenge yourself with a variety of exercises.
How to Interpret Geometry Regents Answers
Understanding how to evaluate and interpret the solutions to mathematical problems is a crucial skill. When reviewing your results, it’s essential to not only know if your answer is correct but also understand why it is correct and how the solution process works. In this section, we’ll explore the steps to properly interpret your responses and analyze the methods used to arrive at the correct solution.
Understanding the Solution Process
Each question typically involves a set of steps that need to be followed to reach the correct result. To effectively interpret the solutions, it’s important to break down each step and recognize how each part contributes to the final answer. Consider the following:
- Identify key concepts: Recognize which concepts are being tested, such as calculating areas, solving for unknowns, or understanding geometric properties.
- Break down the steps: Look at the step-by-step process used to solve the problem, ensuring each part of the solution is logically followed and relevant to the question.
- Check for consistency: Ensure that the answer aligns with known formulas and methods, and verify that all calculations are accurate and complete.
Common Pitfalls to Watch Out For
Even if you follow the right steps, it’s easy to make small mistakes that can lead to incorrect answers. Some common issues to look out for include:
- Misreading the question: Double-check that you’ve understood exactly what the problem is asking, as small misinterpretations can lead to errors.
- Unit conversion errors: Make sure all units are consistent and appropriately converted when necessary.
- Calculation mistakes: Small arithmetic or algebraic mistakes can throw off the entire solution, so it’s essential to carefully review each step.
By carefully reviewing your work and ensuring you understand each part of the process, you can effectively interpret the results of your problem-solving approach. This practice will not only help you in exams but also improve your overall understanding of mathematical principles.
Reviewing Key Concepts for Success
Mastering essential principles is crucial for performing well in any assessment. A thorough review of core concepts not only strengthens understanding but also ensures that you are well-prepared for problem-solving. In this section, we will discuss how to approach the review of fundamental ideas and provide strategies for reinforcing your knowledge.
Core Topics to Focus On
Focusing on fundamental topics will help solidify your understanding and improve your performance. Consider revisiting these key areas:
- Shapes and Properties: Understanding the characteristics of common shapes such as triangles, circles, and polygons is essential. Focus on their properties, including angles, sides, and symmetries.
- Formulas and Theorems: Review essential formulas for areas, volumes, and perimeters, along with critical theorems like Pythagoras’ Theorem and properties of parallel lines.
- Proofs and Logic: Strengthen your logical reasoning and ability to construct formal proofs. Be familiar with the methods used to prove geometric relationships and solve problems.
- Coordinate Systems: Practice working with coordinate geometry, including plotting points, finding distances, and calculating slopes and midpoints.
Effective Study Strategies
To ensure a thorough review, it’s important to implement effective study habits:
- Practice Regularly: Consistent practice is key. Work through problems that cover a wide range of topics to build both speed and accuracy.
- Use Visual Aids: Diagrams and sketches can help visualize problems and make abstract concepts more tangible. Drawing out solutions often clarifies complex ideas.
- Break Down Problems: Divide large, complicated problems into smaller, manageable steps. This method reduces overwhelm and allows for easier problem solving.
- Review Mistakes: Take time to review incorrect solutions. Understand why a particular approach failed and learn how to correct it for next time.
By revisiting these key concepts and adopting productive study strategies, you will build the confidence and knowledge necessary for success. Consistent review of fundamental ideas is the foundation for mastering any topic in mathematics.