
Preparing for technical assessments in computer science requires a strong grasp of essential concepts and techniques. Focused practice is key to mastering fundamental operations and understanding complex algorithms that are often tested in evaluations.
The content of this guide will help you explore important themes and solve typical problems that challenge even experienced learners. By reviewing commonly tested principles, you can enhance your problem-solving abilities and gain confidence for any upcoming evaluations.
Throughout this guide, you’ll find explanations of core topics, examples to reinforce your knowledge, and tips to improve your analytical thinking. Whether you’re just starting or looking to fine-tune your skills, these sections are designed to offer clarity and support.
Data Structure Exam Questions and Answers
When preparing for technical evaluations, understanding core concepts is essential. Grasping the fundamentals and practicing different problem-solving techniques will give you the confidence needed to tackle any challenge. Familiarity with common tasks and strategies can greatly improve your performance.
This section provides a selection of typical challenges, allowing you to test your knowledge and refine your skills. Each example covers a different aspect of the subject, from algorithmic processes to practical implementation. By practicing with these examples, you’ll gain a deeper understanding of key topics.
Additionally, the explanations that follow each problem will guide you in approaching similar challenges during an evaluation. These solutions aim to help you recognize patterns, optimize your methods, and apply your knowledge effectively under pressure.
Key Concepts to Focus On
Mastering the essential elements of any subject requires a deep understanding of its core principles. These foundational ideas not only shape your comprehension but also form the basis for solving complex challenges. Focusing on these critical areas will prepare you to handle a wide range of problems effectively.
Key topics include the manipulation of collections, efficient search and sort techniques, and the analysis of algorithmic efficiency. Knowing how to work with different types of relationships, such as trees or graphs, is equally important, as it opens doors to solving more intricate problems with greater precision.
In addition, understanding how to optimize processes and assess time complexity is crucial. These insights will enable you to choose the most appropriate solutions, saving valuable resources like memory and processing power. Gaining proficiency in these areas will significantly enhance your problem-solving skills.
Top Data Structures to Study
Focusing on the most commonly used techniques will help you tackle a wide variety of problems efficiently. Mastering these key models not only boosts your problem-solving skills but also prepares you to optimize your approach in practical applications. Below are some of the most important concepts to understand and practice.
Arrays and Linked Lists
Arrays are essential for managing collections of items in a fixed-size format, making them highly useful for tasks that require fast access and predictable storage. On the other hand, linked lists provide dynamic flexibility, allowing efficient insertion and removal of elements. Both are fundamental to understanding how to manage memory and manipulate data.
Trees and Graphs
Trees offer a hierarchical way to organize information, with various forms like binary trees being especially important for searching and sorting tasks. Graphs, with their nodes and edges, are crucial for understanding complex relationships such as network connections or traversal paths. Mastering these models opens doors to solving more complex problems in algorithms and system design.
Common Exam Mistakes to Avoid
Many students fall into predictable traps during assessments. Recognizing these common pitfalls and learning how to avoid them can greatly improve your performance. By addressing these issues ahead of time, you can approach your tests with confidence and clarity, ensuring better results.
Rushing Through the Questions
One of the biggest mistakes is rushing through problems without fully analyzing them. It’s important to read each task carefully and ensure that you understand the requirements before attempting a solution. Taking a moment to plan your approach can save valuable time and help avoid careless mistakes.
Neglecting Time Management
Many individuals spend too much time on certain problems and neglect to allocate enough time for others. Practicing good time management is key. It’s advisable to divide your time effectively and prioritize questions based on difficulty and point value. This approach ensures that you tackle the most important tasks without running out of time.
Best Resources for Practice
To truly master the concepts required for technical assessments, it’s essential to have access to high-quality practice materials. Whether you’re looking for interactive platforms, books, or online forums, using a variety of resources can help you build a strong foundation and deepen your understanding. Below are some of the best tools and platforms available for honing your skills.
Online coding platforms such as LeetCode, HackerRank, and CodeSignal offer a wide range of problems that cover both basic and advanced concepts. These platforms not only provide problems to solve but also allow you to view solutions and discuss approaches with a community of learners, making them ideal for continuous improvement.
In addition to online platforms, textbooks and study guides from respected authors can provide in-depth explanations and exercises. Resources like “Introduction to Algorithms” by Cormen et al. or “Algorithms” by Sedgewick are widely recognized and offer comprehensive coverage of core techniques, from sorting to advanced graph theory.
How to Approach Problem Solving
Effective problem-solving requires a structured approach that allows you to break down complex tasks into manageable steps. Whether you’re dealing with a theoretical challenge or a real-world issue, having a clear strategy will help you think critically, choose the best method, and arrive at an optimal solution. This section outlines a proven process that will enhance your problem-solving skills.
Understanding the Problem
The first step in solving any problem is to fully understand what is being asked. Carefully read the description, highlight key elements, and ensure that you identify the inputs, outputs, and constraints. Without this foundational understanding, your efforts might be misdirected.
Planning the Solution
Once you understand the problem, plan how to approach it. Decide on the techniques or algorithms that might be useful, and outline the steps you’ll take to solve it. Consider possible edge cases and evaluate which method offers the best time and space efficiency.
| Step | Description |
|---|---|
| 1. Understand the problem | Read the problem carefully and clarify any ambiguities. |
| 2. Break it down | Divide the problem into smaller subproblems that are easier to handle. |
| 3. Plan your approach | Choose an algorithm or method that best suits the task. |
| 4. Implement the solution | Write the code or steps to execute your plan. |
| 5. Test and optimize | Check if the solution works for all test cases and improve efficiency. |
Understanding Time and Space Complexity
When solving problems efficiently, it’s crucial to evaluate the resources your solution will require, particularly in terms of execution speed and memory usage. Time and space considerations directly affect the performance of an algorithm, especially when dealing with large inputs or complex tasks. This section explores how to measure and optimize these critical aspects.
Time Complexity
Time complexity refers to the amount of time an algorithm takes to complete as a function of the size of the input. Understanding how different algorithms scale with increasing input sizes allows you to select the most efficient approach. Common notations like O(n), O(log n), and O(n^2) describe how the execution time grows relative to the input size.
Space Complexity
Space complexity measures the amount of memory an algorithm uses as the input size increases. It’s important to minimize unnecessary memory usage, particularly in memory-constrained environments. Like time complexity, space complexity is often expressed in terms of big O notation, indicating how memory requirements scale with input size.
Recursive vs Iterative Approaches
When solving computational problems, there are two primary ways to approach them: using recursion or iteration. Both methods have their advantages, but the choice between them can impact efficiency, readability, and ease of implementation. In this section, we’ll explore the differences between recursive and iterative solutions, helping you understand when to use each approach.
Recursive Approach
Recursion involves a function calling itself to break down a problem into smaller, more manageable subproblems. This technique is particularly useful for problems with a clear hierarchical structure, like tree traversal or factorial calculation. However, recursion can be less efficient in terms of memory usage, as each function call adds a new layer to the call stack.
- Best for problems with a natural recursive pattern (e.g., tree operations, divide and conquer algorithms).
- Can lead to clearer, more elegant solutions for certain tasks.
- Potentially more memory-intensive due to deep function call stacks.
Iterative Approach
Iteration, on the other hand, uses loops to repeat a set of instructions until a condition is met. Iterative solutions often provide better performance and are generally more memory-efficient, as they do not require the overhead of function calls. However, they can sometimes be harder to understand or more cumbersome to implement, especially for problems that are inherently recursive in nature.
- Typically more memory-efficient since it avoids the overhead of function calls.
- Can be more complex or less intuitive for certain problems (e.g., tree traversal).
- Preferred for problems where efficiency is critical, such as in large datasets.
Commonly Asked Questions in Exams
When preparing for assessments, it’s essential to anticipate the types of problems you might encounter. Understanding the key topics that are frequently tested will allow you to focus your efforts and approach the material with confidence. This section covers some of the most common themes that regularly appear in assessments, offering insight into what to expect and how to prepare.
Types of Problems You Might Encounter
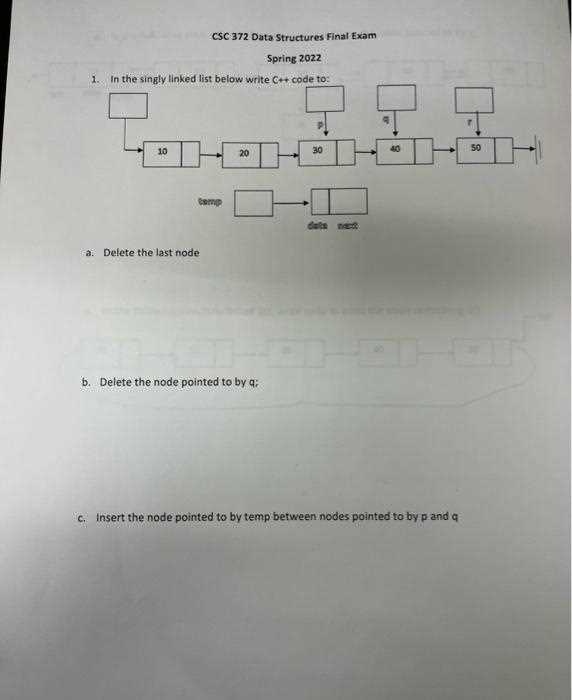
While every assessment can differ, certain types of challenges tend to recur across various tests. Here are some of the most commonly asked problems:
- Problem-solving involving the manipulation of sequences, such as arrays or lists.
- Recursive algorithms and their applications.
- Optimal solutions for sorting or searching techniques.
- Operations on hierarchical models like trees and graphs.
- Time and space complexity analysis of different algorithms.
Sample Problem Formats
Many problems appear in a similar format, allowing you to prepare accordingly. These are typical problem types you may face:
- Code writing: You may be asked to implement an algorithm from scratch.
- Code analysis: You might need to analyze a given solution and determine its efficiency or correctness.
- Conceptual questions: These require you to explain the workings or principles behind an algorithm or data arrangement.
- Problem-solving: These tasks ask you to come up with solutions for specific challenges using the right methods and tools.
Importance of Array Manipulations
Manipulating collections of elements is a fundamental skill in problem-solving, as many tasks involve processing and modifying groups of data. Arrays, being one of the simplest and most versatile forms of data storage, play a crucial role in numerous algorithms and applications. Mastering how to efficiently manipulate arrays can greatly enhance your ability to handle real-world challenges and improve the performance of your solutions.
Why Array Manipulation is Crucial

Working with arrays is essential because they are widely used in various algorithms, especially for tasks that require fast access and modification of elements. Below are some reasons why mastering array manipulation is so important:
- Arrays are often the foundation for more complex data structures and algorithms.
- Efficient array manipulation can significantly improve the time complexity of an algorithm.
- Many problems, such as sorting or searching, rely heavily on array operations.
- Understanding how to manage memory and optimize array usage is vital in large-scale applications.
Common Operations on Arrays
Several key operations are frequently performed on arrays, each serving specific purposes in solving problems. Some of the most common operations include:
- Insertion: Adding an element to a specific position in an array.
- Deletion: Removing an element from an array, which often requires shifting other elements.
- Searching: Finding the index or value of a specific element within an array.
- Sorting: Arranging elements in a specific order, such as ascending or descending.
- Reversing: Reversing the order of elements in an array.
Graph Theory Exam Questions
In many computational assessments, questions related to graph theory are common due to their applicability in a wide range of problems, from network design to social media connections. Understanding graph-based problems and their solutions is essential for tackling complex real-world challenges. In this section, we’ll discuss common problem types you may encounter, focusing on concepts such as traversal, connectivity, and pathfinding.
Key Topics in Graph Theory
Graph theory questions typically focus on the following concepts:
- Traversal algorithms, such as breadth-first and depth-first search.
- Shortest path algorithms like Dijkstra’s and Bellman-Ford.
- Minimum spanning trees and algorithms like Kruskal’s and Prim’s.
- Graph representation methods, such as adjacency lists and matrices.
- Graph connectivity and cycles detection.
Sample Problem Format
Below is a sample of a typical graph-based problem that may appear:
| Problem Type | Key Operations |
|---|---|
| Find Shortest Path | Apply Dijkstra’s algorithm to determine the minimum path between two vertices. |
| Cycle Detection | Use depth-first search to identify cycles in a directed graph. |
| Minimum Spanning Tree | Implement Kruskal’s or Prim’s algorithm to find the tree with the least weight. |
Tree Data Structures Explained
Trees are a powerful and essential tool in organizing data in a hierarchical manner. This type of model allows for efficient storage, retrieval, and manipulation of information, especially when dealing with hierarchical relationships such as organizational charts, file systems, or network routing. Understanding how to implement and navigate these models is critical for solving many computational problems.
At its core, a tree is made up of nodes connected by edges, with one node acting as the root. The rest of the nodes are arranged in a way that each node has a parent and possibly children, forming a branching structure. This model enables fast access to data and supports various operations like searching, insertion, and deletion.
Common Types of Trees
There are several types of tree models, each designed to address specific needs in algorithmic problems:
- Binary Tree: Each node has at most two children, making it a simple yet powerful model for searching and sorting algorithms.
- Binary Search Tree (BST): A type of binary tree where nodes are arranged in such a way that the left child is smaller than the parent, and the right child is larger, allowing for efficient search operations.
- AVL Tree: A self-balancing binary search tree where the height difference between left and right subtrees is at most one, ensuring balanced search times.
- Heap: A complete binary tree used to implement priority queues, where the root node always holds the maximum (or minimum) value.
- Trie: A tree used to store strings in a way that allows for efficient retrieval of words and prefixes, commonly used in autocomplete features and dictionaries.
Operations on Trees

Several fundamental operations are performed on trees, each of which is crucial to maintaining efficient data retrieval:
- Insertion: Adding a new node to the tree while maintaining its properties.
- Traversal: Visiting each node in the tree in a specific order, such as in-order, pre-order, or post-order, to perform operations like searching or printing data.
- Deletion: Removing a node from the tree and reorganizing it to preserve the tree’s structure.
- Searching: Finding a specific node within the tree using traversal methods or direct access based on tree properties.
Linked List Operations in Detail

Linked lists are dynamic data models used to represent a sequence of elements where each element points to the next, allowing for efficient insertion and deletion of nodes. Unlike static arrays, linked lists offer flexibility in managing memory, as elements are not stored in contiguous blocks. Understanding the key operations on linked lists is essential for optimizing performance in many algorithmic problems.
In a linked list, each element, or node, typically consists of two parts: the data itself and a pointer (or reference) to the next node in the sequence. This simple yet powerful structure supports several fundamental operations that are crucial for maintaining the list and ensuring fast access to elements.
Basic Operations on Linked Lists
Below are some of the most common operations performed on linked lists:
- Insertion: Adding a new node to the list, either at the beginning, in the middle, or at the end. The insertion process typically involves updating the pointers of neighboring nodes.
- Deletion: Removing a node from the list. This operation requires updating the pointers of adjacent nodes to ensure the list remains intact after the removal.
- Traversal: Visiting each node in the list from the head to the tail, typically used for operations like printing or searching for a specific element.
- Search: Finding a specific node based on its value. Searching typically involves a linear scan from the beginning of the list until the node is found or the end is reached.
- Update: Modifying the data in a specific node without changing the list’s structure. This operation can be performed during traversal if the desired node is located.
Types of Linked Lists
Linked lists come in several variations, each tailored for different use cases:
- Singly Linked List: Each node points to the next node in the sequence, with the last node pointing to null, indicating the end of the list.
- Doubly Linked List: Each node contains two pointers, one pointing to the next node and another pointing to the previous node, allowing for traversal in both directions.
- Circular Linked List: In this variation, the last node points back to the first node, forming a circular loop. This can be singly or doubly linked, depending on whether one or two pointers are used.
Stacks and Queues in Exams
Both stacks and queues are essential concepts often tested in academic assessments. These concepts deal with the management of collections where the order in which elements are processed plays a critical role. The operations and characteristics of these collections make them fundamental for solving a variety of computational problems, particularly when it comes to handling sequences and managing data flow.
While both stacks and queues involve storing and retrieving data, they differ in how elements are added or removed. Stacks follow a “last in, first out” (LIFO) approach, whereas queues follow a “first in, first out” (FIFO) approach. Understanding the differences between these two models is key when addressing related tasks in problem-solving scenarios.
Common Applications of Stacks
Stacks are widely used in scenarios where the most recently added element needs to be accessed first. Some common applications include:
- Function Calls: The call stack keeps track of function calls in a program, ensuring that the most recent function call is completed before returning to the previous one.
- Expression Evaluation: Stacks are used to evaluate mathematical expressions, especially those involving parentheses or nested operations, by maintaining intermediate results.
- Undo Operations: In applications like text editors, stacks keep track of previous states, allowing users to undo their most recent changes in reverse order.
Common Applications of Queues
Queues are useful in scenarios that require processing elements in the order in which they were added. Some typical applications include:
- Scheduling: Queues are used in scheduling tasks in operating systems, ensuring that tasks are executed in the order they are received.
- Buffering: In data transmission systems, queues help manage the flow of data packets by storing them temporarily until they are processed in order.
- Simulation: Queues model real-world systems such as lines at a bank or customers waiting for service, where each entity must be handled in a fair, first-come, first-served manner.
Hashing Techniques and Applications
Hashing is a technique that transforms input data into a fixed-size value, making it easier and faster to search, retrieve, or store information. This approach plays a crucial role in optimizing various algorithms by ensuring that elements can be accessed in constant time. The process of mapping large amounts of data to a smaller, fixed size helps in reducing the overhead and improving the efficiency of operations, particularly when dealing with large datasets.
There are several methods for achieving hashing, each with its own advantages and drawbacks. These techniques are widely applied in areas such as search engines, databases, and caching systems, where quick access to data is essential. Below, we’ll explore some common techniques and their practical applications in solving computational challenges.
Common Hashing Techniques
Various methods can be employed for hashing, each tailored for specific use cases. Below is a comparison of the most widely used techniques:
| Technique | Description | Use Case |
|---|---|---|
| Division Method | Uses the remainder of dividing the key by a prime number to determine the hash value. | Simple applications where quick and basic hashing is needed. |
| Multiplicative Method | Multiplies the key by a constant, takes the fractional part, and scales it to a hash value. | Effective when a good hash function is required for evenly distributing data. |
| Linear Probing | Resolves hash collisions by checking the next available slot linearly in the hash table. | Useful in situations where table size and collision handling are critical. |
| Separate Chaining | Involves using linked lists to store multiple elements that hash to the same index. | Great for scenarios where collisions are frequent and hash table size may vary. |
Applications of Hashing

Hashing techniques are pivotal in many real-world applications, providing optimized solutions for common computational problems:
- Database Indexing: Hashing is used to create indexes that allow for faster data retrieval, improving query response time.
- Cryptography: In security, hashing algorithms like SHA (Secure Hash Algorithm) are used for data integrity checks and password storage.
- Cache Lookup: Caching systems often use hash tables to store recently accessed data, ensuring quick retrieval and reducing the load on databases.
- Load Balancing: Hashing helps distribute incoming requests evenly across multiple servers by mapping requests to the appropriate server based on a hash value.
Sorting Algorithms You Must Know
Efficiently organizing elements is crucial in many computational tasks. Sorting allows for easier searching, optimal data organization, and can significantly enhance performance, especially when dealing with large datasets. Mastering various techniques for arranging data is essential for solving a wide range of problems and optimizing the performance of algorithms.
Each sorting technique has its advantages, depending on the specific requirements of the task, such as time complexity, space constraints, and the nature of the data. Below are some of the most widely used sorting methods that every programmer should be familiar with:
Key Sorting Algorithms
- Bubble Sort: This simple method repeatedly compares adjacent elements and swaps them if they are in the wrong order. It is easy to implement but not efficient for large datasets due to its O(n²) time complexity.
- Selection Sort: In this technique, the smallest or largest element is selected and swapped with the element at the current position. Although straightforward, it also has O(n²) time complexity, making it inefficient for large datasets.
- Insertion Sort: This algorithm builds the final sorted array one item at a time by inserting elements into their correct position. It is efficient for small datasets or nearly sorted data, with a time complexity of O(n²) in the worst case.
- Merge Sort: A more efficient divide-and-conquer algorithm that splits the data into smaller chunks, sorts them, and then merges them back together. It performs in O(n log n) time, making it much faster than O(n²) algorithms for large datasets.
- Quick Sort: This highly efficient algorithm also uses a divide-and-conquer approach by selecting a pivot element, partitioning the array, and recursively sorting the subarrays. With an average time complexity of O(n log n), it is one of the fastest sorting methods.
When to Use Each Algorithm
Each sorting technique is better suited for different situations. Here’s when you might choose each algorithm:
- Bubble Sort: Useful for small datasets or when simplicity is preferred over performance.
- Selection Sort: Ideal for scenarios where memory usage is a concern, as it performs sorting in-place with minimal overhead.
- Insertion Sort: Best for nearly sorted data or small datasets, as it can outperform more complex algorithms in these cases.
- Merge Sort: Excellent for large datasets where time efficiency is critical, particularly for external sorting.
- Quick Sort: The go-to choice for most general-purpose sorting tasks due to its efficiency in average scenarios.