
In this segment, students will explore a range of essential mathematical principles that form the foundation for more advanced problem-solving techniques. By focusing on these critical skills, learners will enhance their ability to approach complex equations with confidence.
Throughout this chapter, various exercises will be presented, guiding students through the process of solving different types of mathematical challenges. These tasks are designed to improve both speed and accuracy, ensuring a deeper understanding of fundamental concepts.
Comprehensive solutions will be provided to help clarify any confusion, breaking down each step for better comprehension. With these resources, students can strengthen their problem-solving abilities and develop a more intuitive grasp of key mathematical topics.
By mastering the material in this section, learners will be well-prepared to tackle more advanced topics in their mathematical journey. Whether you’re reviewing or learning the concepts for the first time, the structured approach will support long-term success.
Algebra Nation Section 9 Overview

This part of the curriculum delves into key problem-solving techniques that are crucial for mastering mathematical concepts. It introduces a variety of approaches designed to strengthen logical reasoning and enhance analytical skills, providing students with the tools needed to handle complex problems with ease.
The exercises featured here are structured to guide learners through a series of increasingly challenging tasks, each building on the previous one. By working through these problems, students can improve both their understanding and efficiency in solving mathematical equations.
Core Skills Covered
Throughout this chapter, the focus is on developing a deep understanding of fundamental mathematical operations. Concepts such as simplification, factoring, and equation solving are explored in depth, providing a solid foundation for more advanced topics.
Practical Application of Techniques
In addition to theoretical knowledge, students are encouraged to apply what they’ve learned to real-world scenarios. This approach helps reinforce key principles and ensures that students can translate their skills into practical problem-solving strategies, both in and outside of the classroom.
Key Concepts in Algebra Section 9

This section focuses on essential principles that form the backbone of mathematical problem-solving. By understanding these core ideas, students can tackle a variety of equations with greater confidence and precision. The material emphasizes techniques that are not only foundational but also widely applicable in various areas of mathematics.
Some of the most important concepts covered include operations with variables, equation balancing, and methods for simplifying expressions. Each topic is designed to build upon previous knowledge, creating a progressive learning experience that reinforces critical thinking and problem-solving abilities.
| Concept | Explanation | Example |
|---|---|---|
| Variable Manipulation | Changing the values of variables to simplify or solve equations. | x + 5 = 12, solve for x. |
| Equation Balancing | Ensuring both sides of an equation are equal by performing the same operations on both sides. | 2x = 10, divide both sides by 2. |
| Expression Simplification | Reducing expressions to their simplest form for easier analysis. | 3x + 5x = 8x. |
By mastering these concepts, students will develop the skills necessary to solve increasingly complex problems and build a strong foundation for future mathematical studies.
Understanding Section 9 Problem Types
In this part of the curriculum, students are introduced to various problem formats that test their ability to apply mathematical principles effectively. The tasks are designed to assess different aspects of reasoning and calculation, requiring a solid understanding of key concepts. By recognizing the unique characteristics of each problem type, learners can approach each challenge with a tailored strategy.
The problems presented here vary in difficulty, ranging from simple calculations to more complex applications that require multi-step solutions. Some tasks may focus on basic operations, while others may involve interpreting data or solving word problems. Regardless of the format, all problems emphasize critical thinking and accuracy.
Key Problem Types:
- Linear Equations: Problems where students solve for a variable using addition, subtraction, multiplication, or division.
- Word Problems: Tasks that require translating real-world scenarios into mathematical equations to find a solution.
- Expression Simplification: Simplifying complex expressions by combining like terms and applying distributive properties.
- Factoring: Breaking down algebraic expressions into simpler components to solve equations or simplify expressions.
Familiarity with these problem types will not only help students excel in this section but also provide the necessary foundation for more advanced topics in mathematics.
Step-by-Step Solutions for Section 9
This part of the material provides a detailed breakdown of how to approach and solve a variety of problems systematically. By following these step-by-step methods, students can understand the logic behind each solution, which helps to solidify their grasp of core mathematical concepts. The goal is to ensure that learners can solve similar problems independently with confidence.
Each example is presented in a clear and methodical manner, allowing students to follow along and replicate the process. From setting up the problem to finding the solution, these steps serve as a guide to mastering problem-solving techniques.
| Step | Description | Example |
|---|---|---|
| 1 | Identify the problem and what is being asked. | Solve for x in 3x + 4 = 16. |
| 2 | Isolate the variable by using inverse operations. | 3x = 16 – 4 = 12. |
| 3 | Perform the final operation to solve for the variable. | x = 12 / 3 = 4. |
By following these steps, students will build a logical framework for tackling various mathematical tasks, preparing them for more complex challenges in the future.
Common Mistakes in Algebra Section 9

In this part of the study, students often encounter certain errors that can hinder their progress. These mistakes typically stem from misunderstandings of core concepts or skipping crucial steps in problem-solving. Recognizing and addressing these common pitfalls is essential for improving accuracy and building confidence.
By identifying where mistakes frequently occur, learners can refine their approach and avoid falling into the same traps. Understanding the reasoning behind errors and learning how to correct them is an important part of the learning process.
Misunderstanding Operations with Variables
One frequent mistake is mishandling operations involving variables. For example, when simplifying expressions or solving for an unknown, students sometimes forget to apply the correct order of operations or fail to distribute terms properly. This can lead to incorrect solutions that are difficult to trace back to the original mistake.
Overlooking Negative Signs
Another common error involves neglecting negative signs, especially when dealing with subtraction or negative numbers in equations. Failing to correctly account for negative values can throw off the entire solution, leading to errors that are hard to detect without careful review.
By being mindful of these common mistakes and practicing more carefully, students can enhance their problem-solving skills and improve their overall performance in this area.
Practice Exercises for Section 9
Regular practice is crucial for mastering mathematical concepts, and this section offers a variety of exercises designed to reinforce key skills. By engaging with these tasks, students can strengthen their understanding and improve their ability to solve problems efficiently. Each exercise is carefully structured to challenge learners at different levels, ensuring progress through incremental difficulty.
The goal of these practice problems is not only to test knowledge but also to help develop a deeper understanding of the methods involved. As students work through these exercises, they will gain confidence in their problem-solving abilities and be better prepared for more complex challenges.
Basic Operations and Equations
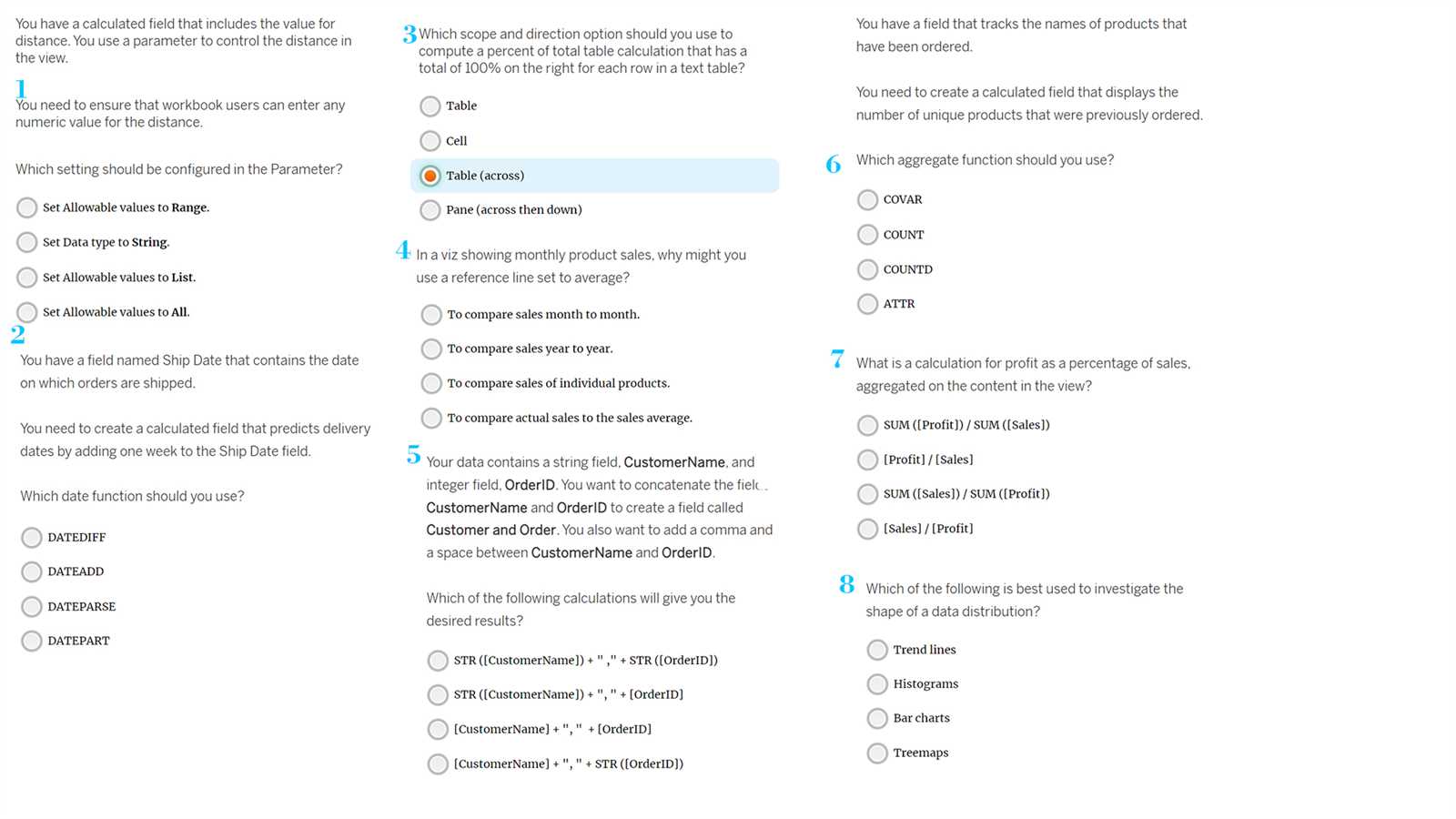
These exercises focus on the fundamental operations needed to manipulate and solve equations. Students will be asked to perform calculations such as addition, subtraction, multiplication, and division, using variables to find unknown values. Completing these tasks will solidify essential skills required for more advanced work.
Applying Formulas and Concepts
In this set of problems, students will apply learned formulas and techniques to solve word problems and more complex equations. These exercises will test the ability to interpret real-world scenarios and translate them into solvable mathematical expressions, reinforcing both conceptual understanding and practical application.
Remember: Practice consistently and review solutions to understand any errors. This will help solidify your skills and ensure long-term success in tackling mathematical problems.
How to Approach Algebra Section 9
Successfully navigating this part of the curriculum requires a strategic approach. Students must focus on understanding the core principles, carefully working through problems, and applying methods consistently. By breaking down the material into smaller, manageable steps, learners can build confidence and develop a deeper understanding of each concept.
Approaching each problem methodically is essential. Start by reading the question carefully, identifying the given information, and recognizing what is being asked. From there, break down the problem into smaller tasks, ensuring that each step is performed correctly. This approach not only helps prevent mistakes but also strengthens problem-solving skills.
Key Steps in Problem Solving
Following a clear sequence of steps is critical to achieving accurate results. Below is an outline of key strategies to use when tackling problems:
| Step | Action | Purpose |
|---|---|---|
| 1 | Read the Problem Carefully | Ensure you understand what is being asked and identify known values. |
| 2 | Set Up the Equation | Translate the given information into a mathematical expression or equation. |
| 3 | Solve Step by Step | Use appropriate operations and methods to isolate the variable. |
| 4 | Double-Check Your Work | Verify your solution by substituting the result back into the original equation. |
Practice and Review
As you work through problems, be sure to review your mistakes and understand where errors may have occurred. Practice regularly and challenge yourself with a range of problems to improve both speed and accuracy. Over time, this will help you approach new tasks with greater confidence and efficiency.
Tips for Mastering Algebra Concepts
Mastering mathematical concepts requires a combination of understanding core principles, regular practice, and applying problem-solving strategies. With the right approach, students can not only improve their skills but also develop a deeper appreciation for the subject. These tips are designed to help learners strengthen their foundation and confidently tackle more challenging problems.
It is essential to break down complex problems into simpler steps and to stay consistent with practice. The more you practice, the more familiar you become with the patterns and techniques required to solve problems efficiently. Additionally, reviewing past mistakes and learning from them is a crucial aspect of improvement.
Understand the Fundamentals
Having a solid grasp of basic concepts is the key to progressing smoothly in this field. Before moving on to more advanced topics, ensure that foundational principles are clear. This includes operations with variables, simplifying expressions, and solving linear equations. Once these core ideas are well understood, tackling more complicated problems becomes easier.
Practice Regularly and Consistently
Frequent practice is one of the most effective ways to improve problem-solving skills. Try working through a variety of problems every day, starting with simpler tasks and gradually increasing the level of difficulty. Consistent exposure to different problem types will help build confidence and speed over time. Quality matters just as much as quantity, so be sure to focus on accuracy in each practice session.
Tip: Use a variety of resources, such as textbooks, online tutorials, and practice problems, to ensure a well-rounded understanding of the material. Don’t hesitate to ask for help when you encounter a particularly challenging problem.
Solving Word Problems in Section 9
Word problems are an important aspect of this area of study, requiring students to translate real-world situations into mathematical expressions and solve them effectively. The key to success in these problems lies in understanding the context, identifying the relevant information, and applying the correct methods step by step. With the right approach, even complex word problems become manageable.
To solve word problems effectively, it’s crucial to break down the information provided, organize it clearly, and develop a strategy for tackling the problem. Here are some useful steps to follow when working through word problems:
Steps to Approach Word Problems
- Read the problem carefully: Understand what is being asked and highlight key pieces of information.
- Identify the variables: Determine what quantities are unknown and assign variables to them.
- Set up an equation: Translate the word problem into a mathematical equation based on the given information.
- Solve the equation: Use the appropriate methods to find the value of the unknown variable(s).
- Interpret the result: Check if the answer makes sense in the context of the problem.
Common Word Problem Types
Word problems come in various forms, but some common types often appear in this section. These include:
- Mixture Problems: These involve combining different quantities, such as liquids or objects, to create a mixture with specific characteristics.
- Rate Problems: These relate to finding the speed, time, or distance of moving objects based on given rates.
- Work Problems: These require determining how long it will take for multiple workers to complete a task when working together.
- Percentage Problems: These deal with calculating discounts, interest, or other percentage-based situations.
By practicing these types of word problems, students can become more proficient in translating real-world scenarios into solvable mathematical equations. The key is to stay organized, remain patient, and apply systematic steps to each problem.
Reviewing Key Formulas for Section 9
Mastering the fundamental formulas is essential for solving problems efficiently in this part of the course. These formulas provide the backbone for solving a wide range of mathematical problems and offer shortcuts that can simplify complex tasks. By reviewing and understanding the key formulas, students can approach problems with confidence and reduce the chances of making errors.
Here are some of the most important formulas that students should become familiar with in order to excel in this area:
Important Mathematical Formulas
- Linear Equations: The general form is Ax + B = C, where A, B, and C are constants, and x is the variable to solve for.
- Quadratic Equations: The standard form is Ax² + Bx + C = 0. The solutions can be found using the quadratic formula: x = (-B ± √(B² – 4AC)) / 2A.
- Exponents: Key properties include a^m × a^n = a^(m+n) and (a^m)^n = a^(m×n).
- Factoring: The difference of squares formula is a² – b² = (a + b)(a – b).
- Ratio and Proportion: The formula a/b = c/d is used to solve problems involving proportional relationships.
Useful Tips for Formula Application
While memorizing these formulas is important, understanding when and how to apply them is even more crucial. Here are a few tips to help:
- Practice regularly: The more you use these formulas, the easier they become to apply in different scenarios.
- Know the context: Make sure to recognize when a problem is best solved with a specific formula, whether it’s a quadratic equation or a ratio.
- Double-check your work: After solving a problem using a formula, verify the solution by substituting it back into the original equation to ensure its correctness.
By consistently reviewing and practicing these essential formulas, students can improve their ability to solve problems accurately and efficiently. Understanding the underlying principles behind each formula allows for better application in a variety of contexts, making complex tasks much simpler to tackle.
Using Visual Aids for Better Understanding
Visual aids can play a crucial role in enhancing comprehension and retention of mathematical concepts. By representing problems graphically, students can gain a clearer understanding of abstract ideas, making complex concepts more tangible and easier to grasp. Visual tools such as graphs, charts, and diagrams help to simplify the problem-solving process and offer a new perspective on solving equations and inequalities.
Incorporating visuals into your study routine can help you break down difficult topics, recognize patterns, and understand relationships between variables. Whether it’s a number line for inequalities or a bar graph for data analysis, these aids support different learning styles and can significantly boost overall performance.
Effective Visual Tools for Mathematical Problems

- Graphs: Plotting equations on a graph helps visualize the relationship between variables and can highlight important features like slopes, intercepts, and asymptotes.
- Tables: Organizing data in tables allows for easy comparison and analysis, particularly in problems that involve sequences or systems of equations.
- Number Lines: A number line is useful for solving inequalities, showing intervals, and understanding positive/negative values.
- Diagrams: For word problems, drawing diagrams or geometric shapes can assist in visualizing the situation, helping to clarify spatial relationships and dimensions.
How to Maximize the Use of Visual Aids
To make the most out of visual aids, follow these strategies:
- Draw the problem: Even if it seems simple, sketching a quick diagram can often reveal insights that are not immediately obvious.
- Label clearly: Ensure all axes, variables, and key points are labeled correctly to avoid confusion.
- Use color: When possible, use different colors to highlight distinct elements of the graph or chart. This can help differentiate between various components of the problem.
By integrating visual aids into your study process, you can improve both your understanding and your ability to solve problems quickly and accurately. This approach is particularly helpful for learners who benefit from seeing concepts in action rather than just reading about them.
Test Prep for Algebra Nation Section 9
Preparing for exams in this area requires a focused approach, as the material covers a variety of concepts that can be challenging without proper preparation. To succeed, it’s essential to review key topics, practice solving problems, and test your understanding with practice questions. A strategic study plan can help you feel confident and perform well when faced with assessments.
Here are several effective steps you can take to maximize your study time and improve your performance on tests:
Effective Study Strategies
- Review Key Concepts: Before diving into practice questions, make sure you have a solid grasp of the core concepts. Focus on topics like equations, inequalities, and factoring techniques.
- Practice Problem-Solving: Work through various examples, starting with easier problems and gradually moving to more complex ones. This will build your confidence and familiarity with different types of questions.
- Use Flashcards: Create flashcards for important formulas, definitions, and properties. Reviewing these frequently will help reinforce your memory.
- Identify Weak Areas: Take note of areas where you struggle and focus on improving them. Seek help from study groups, online resources, or tutors if necessary.
Mock Tests and Time Management
- Take Timed Practice Tests: Simulate real exam conditions by setting a timer and working through practice tests. This helps build time management skills and reduces anxiety during the actual test.
- Track Your Progress: Regularly assess your performance on practice tests and quizzes to gauge your improvement. Focus your review on areas that need the most attention.
- Review Mistakes: After completing practice tests, carefully go over any mistakes. Understand why you got certain questions wrong and how to avoid those errors in the future.
By following these steps and consistently preparing, you can approach the exam with confidence. A combination of practice, reviewing core concepts, and testing yourself will ensure that you’re ready to tackle any challenge that comes your way.
Common Challenges and Solutions

In any complex mathematical study, students often face a range of challenges that can impede progress. Understanding these difficulties and knowing how to overcome them is essential for success. These challenges can vary from conceptual misunderstandings to difficulties in applying formulas correctly. The key to mastering the material is not just identifying these problems, but also finding effective solutions to address them.
Identifying Common Struggles
- Difficulty Understanding Word Problems: Many learners struggle to translate real-world scenarios into mathematical expressions. This often leads to confusion and errors in solving the problem.
- Forgetting Key Formulas: Sometimes, students may remember the steps but forget the crucial formulas that are needed to solve a problem efficiently.
- Time Management Issues: Managing time during tests can be challenging, especially when working through complex problems or lengthy calculations.
- Difficulty with Abstract Concepts: Some topics, like higher-order equations or advanced functions, can seem abstract and hard to grasp without a clear understanding of their underlying principles.
Practical Solutions
- Break Down Word Problems: To improve in solving word problems, start by identifying the key pieces of information in the question. Convert these into a mathematical model and then proceed step-by-step.
- Create Formula Sheets: Keeping a formula sheet handy can help reinforce key equations. Regular practice will make these formulas easier to remember during tests.
- Practice Time Management: Simulate exam conditions by setting time limits for solving practice problems. This will help improve your ability to manage time effectively during the actual exam.
- Visualize Abstract Concepts: Using graphs, diagrams, and visual aids can make abstract concepts more tangible. Try to visualize problems before solving them to better understand the relationships between variables.
By recognizing these common challenges and implementing the appropriate strategies, you can improve your problem-solving abilities and build confidence in your mathematical skills. Overcoming these obstacles will help you not only grasp the material more thoroughly but also perform better in assessments.
How Algebra Section 9 Relates to Other Sections
Understanding the connection between different topics is crucial for building a comprehensive knowledge base. Each part of a mathematical curriculum is designed to build on previous concepts, and Section 9 is no exception. The skills learned in this part are often foundational for mastering more complex topics and solving higher-level problems. Recognizing how these concepts integrate with other areas can significantly enhance a student’s ability to solve problems across various chapters.
Building on Previous Knowledge
- Expanding on Earlier Principles: Section 9 often delves deeper into concepts introduced in earlier sections, such as linear equations and functions. It reinforces and applies these ideas in more complex scenarios.
- Connection with Graphing Techniques: Many topics from Section 9, such as solving inequalities or working with systems of equations, directly relate to graphing techniques covered in earlier lessons. Understanding how to graph equations will be essential for solving problems in this section.
- Preparation for Advanced Topics: The concepts in Section 9 serve as a bridge to more advanced mathematical areas, such as quadratic functions or polynomial equations, which are typically explored in later chapters.
Integrating with Future Topics

- Problem-Solving Skills: The problem-solving techniques developed in Section 9 are essential for tackling more advanced topics, like optimization problems and higher-order polynomials, which students will encounter in later sections.
- Strengthening Analytical Thinking: The analytical skills honed in this part of the curriculum are indispensable for understanding more abstract concepts and applying them in real-world contexts, such as physics or economics.
In essence, Section 9 doesn’t exist in isolation. Instead, it works in tandem with earlier and later topics, creating a cohesive learning experience. The connections between sections allow for a deeper understanding of the material and prepare students for future challenges in mathematics and other related fields.
Using Online Resources for Section 9 Help
In the digital age, students have access to a wealth of online resources that can provide valuable support when tackling challenging topics. These platforms offer a variety of tools, explanations, and examples that can help reinforce the concepts covered in any chapter. Utilizing online resources effectively can enhance understanding and provide the extra practice needed to master complex problems.
Types of Online Resources
- Tutorial Videos: Platforms like YouTube, Khan Academy, and other educational sites offer step-by-step video tutorials that break down difficult topics into easy-to-understand segments. These videos often include visual aids, making them particularly helpful for students who learn best through demonstration.
- Interactive Practice Sites: Websites such as IXL, Mathway, and Wolfram Alpha allow students to practice problems interactively. These sites often provide instant feedback, which helps students identify mistakes and learn from them in real time.
- Online Forums and Discussion Boards: Websites like Stack Exchange or Reddit have communities where students can ask questions and get answers from experienced learners or tutors. These platforms foster collaborative learning and provide a space for discussing complex topics with others.
Benefits of Using Online Resources
- 24/7 Availability: One of the biggest advantages of online resources is their accessibility. Students can access tutorials, practice problems, and expert advice at any time, making it easy to study according to their schedule.
- Diverse Learning Materials: Online platforms offer a variety of learning materials, including written explanations, video lessons, and quizzes. This variety allows students to choose the method of learning that suits them best.
- Real-Time Feedback: Many interactive resources provide instant feedback on exercises, helping students immediately understand their mistakes and correct them before moving on to more difficult problems.
By integrating these online tools into your study routine, you can reinforce your learning, gain additional practice, and build confidence in tackling even the most challenging problems. The availability of diverse resources ensures that you can find the support you need, whether you’re looking for a simple explanation or a more in-depth, interactive experience.
Improving Your Algebra Skills with Section 9
Mastering advanced mathematical concepts requires a combination of practice, understanding key principles, and applying problem-solving techniques. The material covered in this chapter is crucial for developing a strong foundation in higher-level problem-solving, where abstract reasoning plays a significant role. To truly grasp the content, it is essential to approach the exercises methodically and with confidence.
To improve your skills, start by reviewing the fundamental principles that this section emphasizes. Focus on understanding the logical flow of each topic, from basic equations to more complex expressions. Regular practice is vital, as it helps reinforce these concepts and improves both speed and accuracy when solving problems.
Additionally, tackling different types of problems will enhance your ability to adapt to varying scenarios. Try breaking down complicated problems into smaller, manageable parts and solving them step by step. This approach not only strengthens problem-solving abilities but also boosts confidence in applying techniques across a range of exercises.
Finally, using external resources such as video tutorials, online practice exercises, and problem-solving forums can provide additional support. These tools offer varied perspectives and examples that complement your learning and provide alternative methods for tackling tough problems.