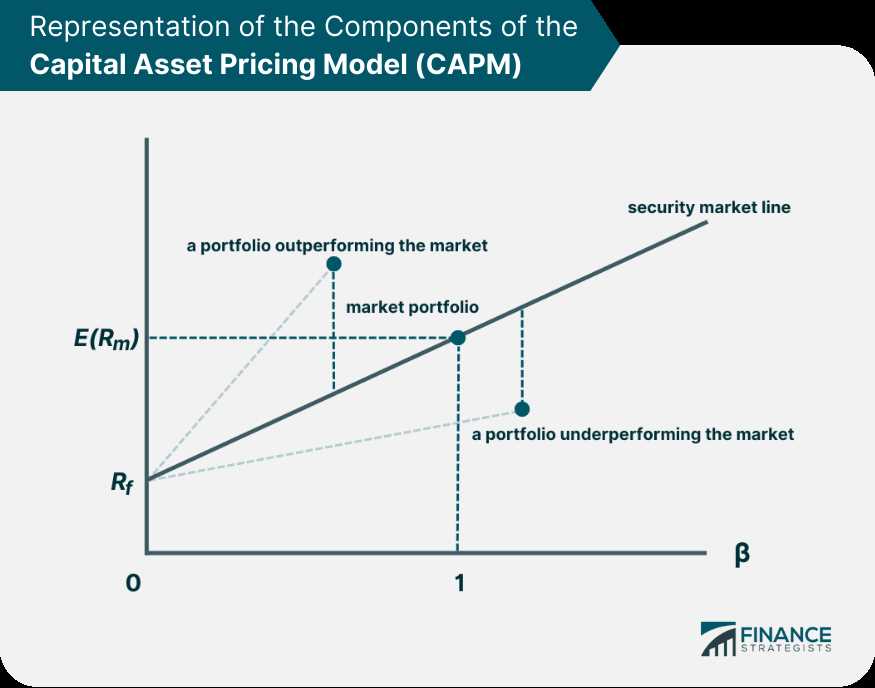
In the world of finance, understanding how to assess the relationship between risk and return is essential. This concept forms the foundation for many investment strategies and decisions. Grasping the core principles behind these calculations is crucial for anyone preparing to tackle related topics in assessments or real-world applications.
Through an in-depth exploration, we will break down various aspects of financial evaluations, emphasizing how to derive meaningful insights from formulas and their practical uses. These concepts help investors make informed choices by estimating potential outcomes and understanding associated risks. A clear understanding can enhance your ability to solve problems and interpret results with precision.
Mastering these techniques not only aids in performing better on evaluations but also prepares you for challenges faced in everyday financial management. From portfolio optimization to performance prediction, these tools provide essential guidance to both students and professionals. By familiarizing yourself with the key principles, you’ll be better equipped to handle any related questions that may arise.
Capital Asset Pricing Model Exam Questions and Answers

This section provides an in-depth exploration of some common scenarios and problems that you may encounter while studying how financial risk and return are evaluated. Understanding these examples is crucial for mastering the underlying principles of investment theory, as well as for effectively applying them in assessments and professional practice.
Common Problems Related to Risk and Return
To prepare for related challenges, it’s important to familiarize yourself with various problem types that assess the ability to determine expected returns based on different factors like risk-free rate, market returns, and beta. By learning to work through these examples, you can solidify your understanding of how the various components influence overall performance.
Example Calculation and Interpretation
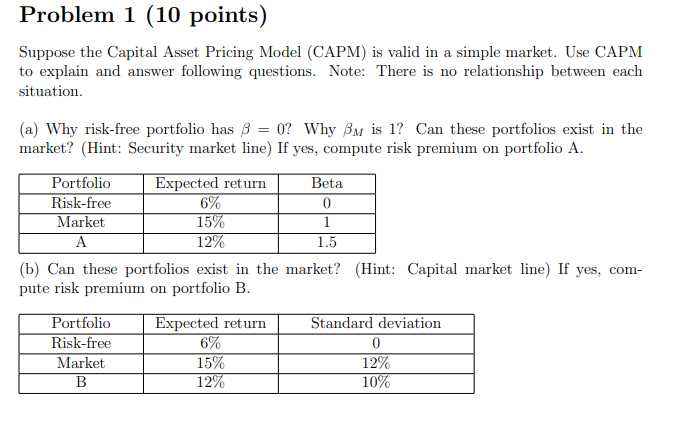
Let’s explore a practical scenario to understand how to apply the core principles and solve related problems. Below is an example table that outlines a typical calculation scenario:
| Risk-Free Rate (%) | Market Return (%) | Beta | Expected Return (%) |
|---|---|---|---|
| 3 | 8 | 1.2 | 9.6 |
| 2.5 | 7.5 | 0.8 | 6.4 |
| 4 | 10 | 1.5 | 13.0 |
In this table, you can see how to apply a basic formula to calculate the expected return. Using a risk-free rate of 3%, a market return of 8%, and a beta of 1.2, the expected return is calculated as 9.6%. Similarly, the table shows how variations in risk factors such as the risk-free rate, market return, and beta impact the expected returns.
By practicing with such examples, you can refine your ability to solve complex problems efficiently. This will help you tackle challenges in both academic and real-world investment scenarios.
Understanding the Capital Asset Pricing Model
The concept explored in this section is fundamental for evaluating how risk influences the potential returns of various investments. It examines the relationship between an investment’s risk and the expected return, providing a framework to make more informed financial decisions. By understanding this relationship, investors can assess how market conditions affect individual securities and create optimized portfolios.
The key idea is to calculate the expected return of an investment by considering factors like market volatility, the overall risk-free rate, and the specific risk associated with the asset. This method helps in determining whether an investment is worth pursuing, given the potential risks involved.
Below is an example table that outlines the components involved in calculating the expected return:
| Risk-Free Rate (%) | Market Return (%) | Beta | Expected Return (%) |
|---|---|---|---|
| 3 | 8 | 1.2 | 9.6 |
| 2.5 | 7.5 | 0.8 | 6.4 |
| 4 | 10 | 1.5 | 13.0 |
This table demonstrates how the risk-free rate, market return, and beta are used to calculate the expected return of an investment. Understanding these components is essential for determining how an individual investment may perform relative to the broader market.
Key Components of CAPM Explained
This section delves into the fundamental elements that form the basis of evaluating financial returns based on various factors like risk, market conditions, and individual asset performance. These components are essential for calculating the expected return of an investment, helping investors make informed decisions about where to allocate their resources. By understanding each factor, you can interpret how different variables affect overall investment outcomes.
The main components include the risk-free rate, the market return, and the asset’s beta, which together help determine the potential return on an investment relative to its risk. Let’s break down these factors for clarity.
| Component | Explanation |
|---|---|
| Risk-Free Rate | This is the return on an investment considered free from risk, often represented by government bonds. |
| Market Return | The average return expected from the entire market, often calculated from historical data. |
| Beta | A measure of an asset’s volatility compared to the overall market. It indicates how sensitive an asset is to market movements. |
Each of these components plays a critical role in determining the expected return of an asset. The risk-free rate sets a baseline, while the market return reflects the broader economic conditions. The beta provides insight into how an individual asset reacts to these conditions, which can significantly impact its overall performance and return potential.
How to Calculate the Expected Return
Calculating the expected return of an investment is essential for making informed decisions. This process involves estimating how much return an investor can anticipate based on specific variables such as risk, market conditions, and asset volatility. The expected return calculation helps in comparing various investment opportunities and assessing whether the potential reward justifies the associated risk.
Steps to Calculate the Expected Return
The formula for calculating the expected return is straightforward, but understanding the components is crucial for accurate application. Below are the essential steps to calculate it:
- Identify the risk-free rate: This is the return on an investment considered free of risk, often represented by government bonds.
- Determine the market return: The market return is the average return of the entire market, typically calculated using historical data.
- Calculate the asset’s beta: Beta measures how much an asset’s value changes in relation to the overall market. A beta greater than 1 indicates higher volatility compared to the market.
- Apply the formula: Use the formula Expected Return = Risk-Free Rate + Beta * (Market Return – Risk-Free Rate) to calculate the expected return.
Example of Expected Return Calculation
Consider the following example to understand how the calculation works in practice:
- Risk-Free Rate: 3%
- Market Return: 8%
- Beta: 1.2
Using the formula, the expected return would be:
Expected Return = 3% + 1.2 * (8% – 3%) = 3% + 1.2 * 5% = 3% + 6% = 9%
This example shows that the investment’s expected return is 9%, factoring in both market performance and the specific volatility of the asset. By understanding these steps, you can accurately assess the return potential of any investment.
Risk-Free Rate and Its Role in CAPM
The risk-free rate plays a fundamental role in assessing the return of investments, serving as the baseline for evaluating the potential rewards from different securities. It represents the return on an investment that carries no risk, typically linked to government bonds, which are considered stable and unaffected by market fluctuations. Understanding this rate is critical as it allows investors to measure how much more they could earn by taking on additional risk.
In the context of the Capital Asset Pricing Framework, the risk-free rate serves as the starting point for calculating the expected return of an investment. By comparing this rate with the market return and factoring in the asset’s volatility, investors can determine if the potential returns justify the risks associated with a particular investment.
The risk-free rate influences the overall expected return, providing a comparison point for more volatile assets. A higher risk-free rate indicates a greater baseline return, which can affect investment strategies and decisions. Investors often rely on this rate to assess whether other investment opportunities, with their associated risks, will provide a worthwhile return above the risk-free rate.
The Role of Beta in CAPM
Beta is a crucial factor in determining the risk associated with a particular investment in relation to the broader market. It measures how sensitive an asset’s return is to the fluctuations in the overall market, reflecting its volatility. A higher beta indicates that the asset is more volatile and will likely experience larger swings in value compared to the market, while a lower beta suggests less volatility.
In financial evaluations, beta helps investors assess the risk of an individual investment relative to the overall market performance. By understanding how an asset moves in relation to the market, investors can predict its behavior under different market conditions and make more informed decisions about risk-taking and portfolio diversification.
Incorporating beta into the investment analysis allows for a more refined calculation of expected returns. A key insight is that an asset with a higher beta will require a higher expected return to compensate for its increased risk. This makes beta an essential tool for gauging the relationship between risk and reward, helping investors build portfolios that align with their risk tolerance and financial goals.
CAPM and Market Portfolio Concept
The concept of a market portfolio is central to understanding how risk and return are distributed across different investments in a well-diversified portfolio. This portfolio consists of all available assets in the market, weighted according to their market value, and serves as a benchmark for evaluating individual securities. The idea is that the market portfolio represents the optimal combination of risk and return, offering the best possible diversification.
In the context of the Capital Asset Pricing Framework, the market portfolio is used to calculate the expected return of a specific asset by comparing its risk against the overall market. The market portfolio acts as a standard, showing how various securities are expected to perform relative to the broader market, which is often characterized by its collective risk and return profiles.
The inclusion of the market portfolio in financial analysis helps investors determine the required return for any asset based on its beta, or sensitivity to market fluctuations. This allows for a more comprehensive assessment of risk, enabling investors to build portfolios that maximize returns while managing exposure to risk. By comparing individual assets to the market portfolio, investors can assess how much additional return is needed to compensate for the risks associated with specific securities.
Calculating the Market Return

Calculating the market return is a vital part of understanding how overall economic conditions influence investment performance. The market return represents the average return expected from all assets in the market, and it serves as a benchmark for comparing individual securities. Accurately calculating the market return allows investors to assess the relative attractiveness of different investments based on their expected performance in relation to the broader market.
The market return is typically derived from historical data, reflecting the performance of a broad market index, such as the S&P 500. It is calculated as the weighted average of the returns of all the assets within that market index. Understanding this return provides investors with a clear reference point to evaluate how individual securities might perform relative to the entire market.
| Step | Description |
|---|---|
| Identify Market Index | Select a broad market index, such as the S&P 500, which reflects the overall market performance. |
| Calculate Returns | Determine the historical return for each asset in the selected index over a specific period. |
| Calculate Weighted Average | Compute the weighted average of returns, based on the market capitalization of each asset in the index. |
Once the market return is calculated, it can be used to compare individual asset returns, helping investors understand whether an asset is likely to outperform or underperform relative to the market. This comparison is essential for making well-informed investment decisions and optimizing portfolio returns.
Interpreting CAPM Equations in Exams
Understanding the equations behind financial theory is crucial for success when dealing with assessments related to investment analysis. The key to interpreting these equations is breaking down each variable and understanding how they relate to the overall calculation of expected returns. Knowing how to approach these equations allows you to solve problems accurately and efficiently, providing clear insights into how risk, return, and market behavior interact.
When interpreting equations in assessments, it’s important to focus on the core components and the relationships they describe. Key terms such as risk-free return, market return, and beta must be clearly understood, as each plays a critical role in the final result. Below are steps to guide you through interpreting and solving equations:
- Understand the Formula: Familiarize yourself with the core equation and its components. The typical structure involves the risk-free rate, the market return, and the asset’s sensitivity to market movements (beta).
- Identify the Variables: Ensure that you can identify each variable in the equation. For example, beta is a measure of risk in relation to the market, while the risk-free rate represents the return from a low-risk investment.
- Apply the Values: Once you have the correct values for each variable, substitute them into the equation. Double-check that all units are consistent and that you are using the correct market data.
- Interpret the Result: After calculating, interpret the result in the context of the given problem. Is the expected return higher than the risk-free rate? Does it make sense given the asset’s risk profile?
By practicing these steps, you can confidently approach CAPM-related questions, ensuring that you apply the concepts correctly and provide well-supported answers. This approach allows for a more organized and efficient way of analyzing financial data, especially when it comes to comparing different investment opportunities.
Common CAPM Questions in Finance Exams
When preparing for assessments related to financial theory, it’s important to familiarize yourself with the types of problems that frequently appear. These questions often focus on understanding the relationship between risk, return, and the broader market. By practicing the most common types of problems, you can improve your ability to apply the relevant concepts and formulas to real-world scenarios.
Typically, questions related to financial theory may ask you to calculate the expected return of a specific investment, determine the required return based on market conditions, or assess the impact of changes in risk factors. Below are some common types of problems you might encounter:
- Expected Return Calculation: These questions require you to use the formula to calculate the expected return of a particular asset, given its beta, the market return, and the risk-free rate.
- Risk Analysis: Here, you may be asked to interpret the risk level of an asset by comparing its beta to the market or other investment options.
- Impact of Market Changes: These questions involve analyzing how changes in market conditions, such as shifts in the risk-free rate or market return, affect the expected return of a particular security.
- Portfolio Construction: In these scenarios, you are asked to consider how a set of investments interacts with the market and determine the portfolio’s overall return or risk profile.
- Comparing Investments: These questions ask you to evaluate different investment opportunities by comparing their expected returns, given their individual risk profiles.
Familiarizing yourself with these types of problems will help you approach questions confidently and accurately. Understanding the underlying principles behind each problem is essential for delivering well-structured solutions and demonstrating a strong grasp of financial theory in assessments.
Analyzing Risk and Return in CAPM
Understanding the relationship between risk and return is fundamental to making informed investment decisions. In financial theory, this relationship is often explored through the concept of risk premiums, where the expected return on an investment is linked to the risk it carries compared to a risk-free asset. By analyzing the risk profile of an asset and its potential return, investors can assess whether the investment justifies the level of risk taken.
The primary tool for analyzing this relationship involves the calculation of expected returns, which incorporates both market performance and individual risk factors. A critical element in this analysis is the beta coefficient, which measures an asset’s volatility relative to the broader market. A higher beta indicates greater risk, and thus a higher potential return, while a lower beta suggests less risk and a more stable return.
Risk and return analysis often involves comparing various assets or portfolios to determine which ones align best with an investor’s risk tolerance. It also requires understanding how market fluctuations impact individual returns and assessing whether the return justifies the risk undertaken. Below is a breakdown of key steps to perform this analysis:
- Risk Measurement: Assess the volatility of an asset using beta, which represents its correlation with overall market fluctuations.
- Expected Return Calculation: Use the formula for expected return, considering the risk-free rate, the market return, and the asset’s beta to determine the potential return.
- Comparison of Assets: Compare different investment options based on their risk-return profiles to find the optimal investment according to your objectives.
- Portfolio Risk Analysis: When dealing with multiple assets, assess how the portfolio’s overall risk aligns with the expected returns, factoring in the correlation between the assets.
By carefully analyzing the risk-return trade-off, investors can make more informed decisions that align with their financial goals and risk preferences. This process helps ensure that each investment decision is backed by a logical assessment of both the potential rewards and the inherent risks involved.
CAPM Assumptions and Limitations
When using financial theories to assess investments, it’s crucial to understand the foundational assumptions upon which these models are built, as well as their limitations. While these models provide valuable insight into risk and return, they also rely on certain idealized conditions that may not always align with real-world scenarios. By recognizing these assumptions and limitations, investors can better evaluate the practical applicability of the model in different contexts.
The underlying assumptions of this framework are designed to simplify the complex dynamics of financial markets, but they also contribute to certain constraints. The model assumes perfect market conditions and rational investors, which in practice may not always hold true. Additionally, the theory assumes that all market participants have access to the same information and that there are no transaction costs, which can be far from reality in actual financial markets.
Key Assumptions
- Efficient Markets: Markets are assumed to be fully efficient, meaning that all available information is reflected in asset prices.
- Rational Investors: Investors are assumed to act rationally, seeking to maximize their returns while minimizing risk.
- No Transaction Costs: The theory assumes there are no costs associated with buying or selling assets.
- Single Period Investment Horizon: The model assumes that investors make decisions based on a one-period investment horizon, typically focusing on a short time frame.
- Homogeneous Expectations: All investors are assumed to have the same expectations regarding future returns, which may not reflect the diversity of opinions in real markets.
Limitations of the Model
- Unrealistic Assumptions: Many of the assumptions, such as no transaction costs and perfect market efficiency, do not hold true in practice, making the model less reliable in some cases.
- Market Anomalies: Real-world markets often exhibit inefficiencies, such as behavioral biases and information asymmetries, which the model does not account for.
- Ignoring Taxes and Inflation: The model assumes that there are no taxes or inflation, which can significantly affect the real return on investments.
- Single Period Limitation: The model’s focus on a one-period horizon overlooks the complexities of long-term investing, where different factors may come into play.
While the model offers a useful framework for understanding risk and return, its practical limitations must be kept in mind. Investors should consider these assumptions when applying the model to real-world scenarios and supplement it with additional analysis to make well-informed decisions.
Practical Applications of the CAPM
The theoretical framework that measures the relationship between risk and expected return can be applied in various real-world situations, providing valuable insights for investment decisions. By assessing the risk of a particular investment relative to the market, this framework helps investors determine the fair expected return on their investments. However, its practical use extends beyond theoretical understanding and has applications in portfolio management, cost of capital calculations, and asset pricing.
Portfolio Management
One of the key uses of this framework is in portfolio management, where it helps in optimizing the risk-return profile of an investment portfolio. By understanding how individual assets relate to overall market movements, investors can diversify their holdings to reduce risk while maintaining an optimal expected return. The framework assists in selecting the right mix of assets by identifying those that offer the best return for the level of risk taken.
Calculating Cost of Capital
This framework is widely used to calculate the cost of equity capital, which is an essential input in many financial models. By using the risk-free rate, the expected market return, and the asset’s beta, companies can estimate the return required by investors for holding their equity. This cost of equity is crucial for firms when determining the appropriate discount rate to use in capital budgeting and valuation of future cash flows.
Asset Valuation
Another practical application of the theory is in asset valuation. The model provides a method for determining the expected return on an investment, which can then be used to estimate its fair value. Investors can compare the expected return with the actual return on the asset to determine whether it is undervalued or overvalued in the market. This approach helps investors make informed decisions about buying or selling assets based on their risk-return profiles.
While the framework offers valuable insights, it’s important to remember that its practical application requires careful consideration of its assumptions and limitations. When used appropriately, it can help investors make better decisions regarding portfolio construction, capital investment, and valuation strategies.
Differences Between CAPM and APT
While both the framework that evaluates the relationship between risk and return and the Arbitrage Pricing Theory (APT) are used to determine expected returns, they are grounded in different principles and make distinct assumptions. Each theory provides a unique approach to understanding how different factors influence investment returns, and the way they handle risk and market dynamics differs significantly.
Key Differences
- Underlying Assumptions: The first framework operates under the assumption of a single factor, the market risk, being the primary determinant of returns. It relies on the idea that the market portfolio captures all relevant risk. In contrast, APT is based on the concept of multiple factors affecting returns, allowing for a more flexible and nuanced approach to risk assessment.
- Risk Factors: In the framework, the sole risk factor is the overall market risk (beta). APT, however, considers several macroeconomic and company-specific factors such as inflation, interest rates, and changes in the business cycle, which can all influence returns.
- Simplicity vs. Flexibility: The first approach is relatively simpler, with its reliance on just one factor making it easier to understand and apply. APT, on the other hand, offers more flexibility as it does not specify the exact risk factors, allowing analysts to select variables based on the context and environment of the market.
- Mathematical Formulation: The framework is expressed in a linear equation that links the expected return to the risk-free rate, the market return, and the asset’s sensitivity to market movements (beta). APT also uses a linear structure but incorporates multiple risk factors, which leads to a more complex formula.
- Assumption of Market Efficiency: The first approach assumes perfect market efficiency where all investors have access to the same information and act rationally. APT does not rely on this assumption and allows for the possibility of market inefficiencies, making it more adaptable to real-world conditions.
Conclusion
Both frameworks provide valuable tools for assessing investment returns, but the choice between the two depends on the specific circumstances and the complexity of the analysis required. The first theory offers simplicity and ease of use, while APT provides a more robust and flexible method for accounting for multiple risk factors. Understanding these differences can help investors and analysts decide which theory is best suited for their financial models and strategies.
CAPM and Portfolio Diversification
When it comes to building an investment portfolio, diversification is a key principle used to reduce overall risk. By combining different assets, investors aim to minimize the impact of any single investment’s poor performance on the total return. The framework for understanding the relationship between risk and return offers valuable insights into how diversification affects an investment portfolio, particularly in terms of risk management and optimizing expected returns.
How Diversification Works in Risk Reduction
One of the central tenets of the first framework is that investors can reduce unsystematic risk (the risk specific to individual assets) through diversification. The theory suggests that by holding a variety of investments across different sectors, industries, and asset classes, an investor can significantly reduce the unpredictable volatility tied to any single asset. This is because, as the number of assets in a portfolio increases, the total risk becomes more influenced by the market risk, which cannot be eliminated by diversification alone.
Implications for Portfolio Construction
In the context of the framework, the efficient frontier represents the optimal set of portfolios that offer the highest expected return for a given level of risk. Diversification plays a crucial role in shaping this frontier by reducing the overall portfolio risk while maintaining an acceptable level of return. The more diversified a portfolio is, the closer it gets to the optimal point on the frontier, where risk is minimized, and returns are maximized.
However, it’s important to note that diversification does not eliminate all types of risk. The framework primarily focuses on systematic risk, which is linked to broader market factors, such as interest rates, inflation, or economic downturns. While diversification can help mitigate the impact of specific risks, it cannot protect an investor from market-wide factors that affect all assets.
Exam Preparation Tips for CAPM Questions
Preparing for questions related to financial theory requires a solid understanding of key principles, formulas, and their practical applications. For those tackling problems related to risk, return, and investment strategies, a systematic approach is essential. Below are some useful tips to effectively prepare for such topics.
Focus on Key Concepts
Start by familiarizing yourself with the foundational concepts that underlie the framework. Understanding the relationship between risk and return, as well as the role of various financial variables, is crucial for solving problems. Make sure you grasp the following areas:
- Risk-Free Rate: Know how to identify and interpret this crucial component in the calculations.
- Market Risk: Understand how it affects individual investments and overall portfolio returns.
- Beta: Learn how to interpret the risk associated with specific investments compared to the broader market.
Practice with Real-Life Scenarios
Applying theoretical knowledge to real-life scenarios is essential for mastering complex concepts. Practice with a variety of problems, ranging from basic calculations to more intricate scenarios involving multiple variables. Some preparation exercises to consider:
- Calculating Expected Return: Solve for expected returns using given values of market risk, risk-free rates, and beta.
- Portfolio Diversification: Practice calculating how diversification reduces overall risk.
- Interpreting Equations: Review various financial equations and how they relate to decision-making in investing.
Master the Formulas
While conceptual understanding is essential, knowing the formulas is also key to success. Be sure to memorize the relevant equations and practice applying them under timed conditions:
- Return Calculation: Know the formula for expected return and how to use it in different contexts.
- Risk Assessment: Understand how to use beta and the market risk premium to assess the risk of an individual investment.
Review Common Mistakes
Identifying and avoiding common errors can save valuable time during your preparation. Some common mistakes to watch for include:
- Misinterpreting the market return or risk-free rate.
- Confusing beta values or incorrectly calculating portfolio diversification benefits.
- Failing to account for systematic vs. unsystematic risk in portfolio construction.
By focusing on these areas, practicing with realistic examples, and consistently reviewing your understanding of the underlying principles, you’ll be better equipped to tackle the relevant problems efficiently and accurately.
Common Mistakes in CAPM Exam Answers
While working through financial theory problems, there are several pitfalls that students often encounter. These mistakes can stem from misinterpretation of concepts, improper application of formulas, or simple calculation errors. Recognizing and avoiding these common missteps can greatly enhance your performance when tackling related questions.
1. Misunderstanding the Risk-Free Rate

One of the most frequent errors involves the misinterpretation of the risk-free rate. Some students incorrectly assume it is the rate of return on any government bond, without considering the time frame or other relevant factors. In fact, the risk-free rate should represent the return on an investment that carries no risk of financial loss, typically government securities with short-term maturities.
2. Confusing Beta with Market Return
Another common mistake is confusing the concept of beta with the overall market return. Beta is a measure of an individual asset’s volatility relative to the market, not the return. Using beta to directly calculate the return will lead to incorrect conclusions. It’s essential to understand that beta helps assess risk, but it’s not the same as expected return.
3. Incorrect Application of the Formula
Students often make errors when applying the formula for expected returns. For instance, when calculating the return of a specific asset, the market risk premium must be multiplied by the asset’s beta before adding the risk-free rate. Failing to do so in the correct order leads to faulty results. Make sure to carefully follow the sequence and apply the formula step by step:
- Expected Return = Risk-Free Rate + Beta × (Market Return – Risk-Free Rate)
4. Overlooking the Assumptions
Another frequent error is neglecting the underlying assumptions of the theory, such as the idea of perfect markets and no transaction costs. These assumptions are important because they influence the interpretation of results. When answering questions, remember that the theoretical framework relies on these simplified conditions, which may not always hold in real-world scenarios.
5. Failing to Account for Diversification
In portfolio-related questions, some students fail to incorporate the benefits of diversification. Diversifying assets can reduce the overall risk of a portfolio, yet this is often overlooked when discussing individual asset returns. Understanding how diversification works in reducing unsystematic risk is crucial for answering questions about portfolio construction effectively.
By identifying these common mistakes and ensuring a clear understanding of each concept, you’ll be able to approach similar questions with greater accuracy and confidence.
How to Improve Your CAPM Knowledge
Mastering financial theories and concepts requires a structured approach. To effectively grasp the key ideas surrounding risk, return, and market relationships, one must engage with the material from multiple angles. Whether you are starting from scratch or aiming to enhance your existing understanding, the following strategies will help deepen your expertise and improve your ability to apply these concepts in practical situations.
1. Strengthen Your Theoretical Foundation
A solid understanding of the fundamental principles is essential for mastering any financial framework. To improve your knowledge, ensure you fully grasp the following concepts:
- Risk-Free Rate: Understand its role as a baseline for expected returns.
- Beta: Learn how beta reflects an asset’s risk relative to the overall market.
- Market Risk Premium: Familiarize yourself with the difference between the market return and the risk-free rate.
- Expected Return: Practice calculating expected returns using the core formula.
2. Apply Real-World Examples
Theoretical knowledge becomes much clearer when you apply it to real-world scenarios. Use financial news, case studies, and company reports to explore how professionals use these concepts to make investment decisions. Try to:
- Analyze historical data and calculate expected returns for different assets.
- Identify the beta of various stocks and understand how it affects their expected performance.
- Examine market conditions and assess the implications for expected returns.
3. Engage in Practice Problems
To solidify your knowledge, regularly work on problems related to risk-return analysis. Solving practical problems helps you become familiar with the mechanics of calculations and deepens your understanding of underlying concepts. Use textbooks, online courses, or academic papers to find practice exercises.
4. Participate in Study Groups
Learning from others can provide valuable insights. Join a study group where you can discuss difficult concepts, share resources, and challenge each other’s understanding. Teaching others is also a great way to reinforce your own learning.
5. Stay Updated on Financial Research
Stay informed about advancements in finance and new methodologies by reading financial journals and industry reports. This will help you understand how the core concepts evolve and are applied in the modern financial landscape.
By following these strategies, you will develop a deeper understanding of financial principles and improve your ability to analyze risk and return in any market. Consistent practice and real-world application are key to mastering this area of finance.