
Success in any professional field relies on a solid understanding of fundamental concepts, and the initial evaluation plays a crucial role in determining readiness. For those looking to pursue a career in healthcare, mastering the required subjects is essential. This section will provide the necessary tools and strategies to approach the assessment with confidence.
In particular, the quantitative portion of the evaluation requires focus and practice. It tests one’s ability to apply various principles in problem-solving scenarios, ranging from basic operations to more complex calculations. With the right preparation, even the most challenging questions can be approached systematically and solved effectively.
Effective preparation for this part of the evaluation involves more than just memorization; it requires developing critical thinking skills and practicing problem-solving techniques. By honing these skills, you can ensure that you are well-equipped to tackle the most demanding tasks and increase your chances of success in the assessment process.
Kaplan Nursing Entrance Exam Math

For individuals pursuing a career in healthcare, understanding numerical concepts is an integral part of the qualification process. The assessment tests the ability to apply essential mathematical skills in real-world situations, focusing on critical thinking and problem-solving. Success in this section relies not only on knowing formulas but also on the capacity to use them in various contexts effectively.
The skills evaluated in this section include arithmetic, algebra, data interpretation, and basic geometry. To perform well, one must become familiar with the types of questions that are commonly asked, as well as the strategies for solving them accurately and efficiently.
| Topic | Key Skills |
|---|---|
| Basic Arithmetic | Addition, subtraction, multiplication, division |
| Algebra | Solving equations, working with variables |
| Fractions and Percentages | Converting fractions, calculating percentages, ratios |
| Data Interpretation | Reading charts, graphs, and tables |
| Geometry | Understanding shapes, area, perimeter, volume |
By mastering these core areas, candidates will be better equipped to handle the challenges that this section presents. Regular practice and review of key topics will help improve both speed and accuracy, leading to a more confident performance.
Overview of Kaplan Nursing Exam
This assessment is a critical component for individuals aspiring to enter the healthcare profession, as it evaluates the essential skills needed for academic and professional success. The test is designed to measure a variety of abilities that are necessary for excelling in a rigorous program. Candidates are expected to demonstrate proficiency in both theoretical knowledge and practical application across multiple areas of study.
Although the evaluation covers several domains, it is structured to focus on key concepts that are essential for future healthcare roles. The ability to solve problems efficiently, analyze data, and apply critical thinking is emphasized throughout the process. This comprehensive approach ensures that only candidates who meet the required standards are selected for the next stage of their training.
Key Math Topics to Focus On
When preparing for an assessment that evaluates quantitative reasoning, it’s essential to focus on the foundational topics that are commonly tested. A strong grasp of these subjects will ensure that you can approach the problems with confidence and precision. By honing skills in the most critical areas, candidates can increase their chances of achieving a higher score and successfully progressing in their academic journey.
Core Topics to Master

| Topic | Skills Involved |
|---|---|
| Basic Arithmetic | Operations with whole numbers, decimals, and fractions |
| Algebra | Solving linear equations, working with variables, and expressions |
| Proportions and Percentages | Solving ratio problems, calculating percentages, and conversions |
| Data Interpretation | Understanding charts, graphs, and tables |
| Geometry | Calculating areas, perimeters, and understanding geometric properties |
Why These Topics Matter

These areas are crucial for solving a wide range of problems that reflect real-world scenarios. A deep understanding of these topics allows for more efficient problem-solving, faster calculations, and better decision-making. Mastering these key concepts will give you the ability to tackle various question types, from basic operations to complex problem-solving tasks, with ease.
Understanding the Math Section Format
To succeed in the quantitative portion of the assessment, it’s important to understand the structure and types of questions that will be presented. This section is designed to test your ability to apply various numerical skills to solve practical problems. Familiarity with the format helps in strategizing your approach and managing your time effectively during the test.
Question Types and Structure
The assessment typically includes a variety of question formats, ranging from simple calculations to more complex problem-solving scenarios. Some questions may present a direct mathematical problem, while others might involve real-world situations that require you to apply theoretical knowledge in a practical context. In most cases, you will be asked to choose the correct answer from multiple options.
Time Management and Strategy
Given the time constraints of the test, it is crucial to have a clear strategy. Effective time management allows you to allocate enough time to each question while avoiding getting stuck on difficult problems. Quick decision-making and prioritizing easier questions first can help you maximize your score without feeling rushed.
Tips for Improving Math Skills
Enhancing your ability to solve numerical problems requires both practice and the development of strong problem-solving strategies. By focusing on key techniques and regularly practicing, you can increase your proficiency and speed in tackling a wide range of questions. Consistent effort in sharpening your skills will build confidence and lead to better performance in any assessment.
One of the most effective ways to improve is through targeted practice. Start by reviewing basic principles, then gradually work on more complex problems. Break down difficult problems into smaller steps to make them more manageable. Additionally, reviewing your mistakes helps to identify areas that need further attention and refining your approach to similar questions.
Another crucial tip is to use a variety of resources for practice, such as workbooks, online exercises, and practice tests. Each resource offers different types of problems, which will help strengthen your overall understanding. Staying consistent with practice, while making sure to review new concepts regularly, will ensure steady progress.
Essential Math Concepts for Nurses

For individuals pursuing a healthcare career, certain numerical concepts are fundamental to daily responsibilities. Whether administering medication, calculating dosages, or interpreting medical data, a solid grasp of these skills is essential for ensuring accuracy and providing safe patient care. Understanding these core topics enables healthcare professionals to make quick, informed decisions under pressure.
Key Concepts to Master

- Unit Conversions: Converting between units such as milliliters, liters, and grams is essential for accurate medication dosing.
- Fractions and Decimals: Understanding fractions and decimals is crucial for performing dosage calculations and understanding test results.
- Percentages: Many medical calculations involve percentages, such as determining drug concentrations or blood volume percentages.
- Ratios and Proportions: Nurses use ratios to calculate the right amounts of medication based on a patient’s weight or age.
Practical Applications

- Administering proper medication dosages based on a patient’s weight or age.
- Calculating IV flow rates and determining how long an infusion should take.
- Interpreting lab results such as blood glucose levels or cholesterol ratios.
- Understanding vital signs and applying normal ranges to patient care.
Mastering these fundamental concepts ensures healthcare professionals are prepared for a wide range of real-world situations, from basic tasks to complex clinical scenarios. Regular practice and continued education in these areas will reinforce the ability to apply them accurately and efficiently in everyday practice.
Time Management During the Test
Effective time management is crucial when taking any assessment, as it helps ensure you can complete all sections within the given time frame. Managing your time wisely reduces stress and allows you to focus on answering questions accurately. By adopting a structured approach, you can maximize your performance and avoid rushing through the most challenging parts of the test.
Key Strategies for Managing Time
- Familiarize Yourself with the Format: Before the test, review the structure and types of questions to understand how much time each section may require.
- Prioritize Easier Questions: Start with the questions you find easier to build confidence and save time for more complex problems.
- Avoid Spending Too Much Time on One Question: If you’re stuck, move on to the next question and come back later if you have time.
- Use the Process of Elimination: When unsure of an answer, eliminate the clearly incorrect options to increase your chances of selecting the right one quickly.
How to Pace Yourself
- Divide the total time by the number of questions to estimate how much time to spend on each one.
- Set a timer for each section to help you stay on track and avoid spending too long on any one part.
- During the test, periodically check the clock to ensure you’re not falling behind and adjust your pace if needed.
With proper time management, you can approach the test with a calm and focused mindset, making it easier to work through each section efficiently and effectively.
Practice Questions for Math Success
Practicing with sample questions is one of the most effective ways to improve your problem-solving skills. These practice exercises help familiarize you with the types of problems that will appear on the test and allow you to refine your approach to answering them. Regular practice boosts confidence and ensures you are prepared for a variety of question formats.
By working through practice problems, you can identify areas where you may need further review and fine-tune your techniques for solving different types of questions. Whether the problems are simple or complex, consistent practice helps you to manage time better and increases your accuracy in calculating answers.
Below are some examples of practice questions:
1. Convert 3/4 to a decimal.
Solution: 3 ÷ 4 = 0.75
2. A solution is 20% alcohol. How many milliliters of alcohol are in 200 ml of solution?
Solution: 200 × 0.20 = 40 ml of alcohol
3. If a patient needs 0.5 mg of a medication and you have a bottle that contains 250 mcg per tablet, how many tablets should you give?
Solution: 0.5 mg = 500 mcg, so 500 ÷ 250 = 2 tablets
Practicing these types of questions regularly will help strengthen your understanding and allow you to approach the real assessment with greater ease and speed. The more problems you solve, the more confident you will feel on test day.
How to Approach Word Problems
Word problems can often seem daunting because they require you to extract relevant information from a detailed description and apply mathematical concepts to solve them. However, with a structured approach, these problems become much more manageable. By breaking down the question into smaller, more understandable parts, you can identify the key components needed to reach the solution.
The first step in solving word problems is to carefully read the entire question. Take note of the important numbers, units, and relationships between them. Once you’ve identified this key information, translate it into a mathematical equation or expression. Remember to stay focused on what the problem is asking, and avoid getting distracted by unnecessary details.
Step-by-Step Process
- Read the problem thoroughly: Understand the context and identify the variables.
- Highlight important information: Pay attention to numbers, units, and key terms.
- Translate to an equation: Convert the verbal information into mathematical terms.
- Solve the equation: Perform the necessary calculations based on the equation.
- Double-check your answer: Ensure that the solution makes sense within the context of the problem.
Example Word Problem
Here’s an example of how to approach a word problem:
| Problem | A patient is prescribed 500 mg of medication. If each tablet contains 250 mg, how many tablets should the patient take? |
|---|---|
| Solution Steps |
|
By following these steps and practicing regularly, you’ll develop a systematic approach to solving word problems, making them less intimidating and more manageable to solve.
Strategies for Algebra and Ratios
Algebra and ratios are fundamental concepts that play a crucial role in many problem-solving situations. They allow you to express relationships between quantities and solve for unknown values. Understanding how to manipulate algebraic expressions and work with ratios efficiently is key to tackling various types of questions in a structured manner.
When approaching algebraic problems, it’s important to identify the variables and relationships between them. Simplifying the equation step by step and isolating the unknown value can help clarify the problem. In ratio problems, focus on understanding the proportional relationship between the quantities involved. Whether you’re comparing amounts or solving for an unknown part of the ratio, it’s essential to apply the right approach to ensure accurate results.
Here are some effective strategies:
- For Algebra:
- Start by simplifying the equation and combine like terms.
- Use the distributive property to expand expressions when necessary.
- Isolate the variable by performing inverse operations to both sides of the equation.
- Check your solution by substituting the value of the variable back into the original equation.
- For Ratios:
- Write the ratio as a fraction and cross-multiply when solving for unknown values.
- Set up equivalent ratios to find the missing value, ensuring the proportions remain consistent.
- When working with word problems, translate the text into a numerical relationship before solving.
By practicing these strategies and applying them systematically, you can enhance your ability to solve algebraic and ratio problems efficiently. The more you practice, the more confident and accurate you will become in handling these essential concepts.
Mastering Fractions and Percentages
Fractions and percentages are crucial tools for comparing quantities and expressing parts of a whole. Whether you’re working with basic fractions or calculating percentages, understanding the fundamental principles behind these concepts is essential for solving a wide range of problems. Mastery of these skills enables you to handle everyday situations such as budgeting, dosage calculations, and interpreting data.
Fractions represent a part of a whole and can be simplified, added, subtracted, multiplied, or divided. Percentages, on the other hand, are simply a fraction expressed out of 100. Learning how to convert between fractions, decimals, and percentages is vital for accuracy and efficiency in solving various problems. The ability to manipulate these values fluidly ensures you can tackle problems with ease.
Here are key strategies to master these concepts:
- For Fractions:
- Convert fractions to their simplest form by dividing both the numerator and denominator by their greatest common divisor (GCD).
- When adding or subtracting fractions, ensure they have a common denominator before proceeding.
- For multiplication, multiply the numerators and denominators directly.
- For division, multiply by the reciprocal of the second fraction.
- For Percentages:
- To convert a fraction to a percentage, multiply the fraction by 100.
- To find a percentage of a number, multiply the number by the percentage and divide by 100.
- To calculate the percentage increase or decrease, subtract the old value from the new value, divide by the old value, and multiply by 100.
Example Problems:
- Fraction Simplification: Simplify the fraction 18/24.
- Solution: Divide both the numerator and denominator by 6 to get 3/4.
- Percentage Calculation: What is 25% of 200?
- Solution: (25/100) × 200 = 50.
Regular practice with fractions and percentages will help you become more comfortable with these operations. By applying the strategies above, you will gain the confidence to solve these problems quickly and accurately.
Geometry Skills for the Kaplan Exam
Geometry is a vital area of study for anyone preparing for tests that assess mathematical reasoning. It involves the study of shapes, sizes, and the properties of space. Whether you’re calculating areas, volumes, or understanding the relationships between different geometric figures, having strong geometry skills is essential for tackling many types of questions. Building a solid foundation in this field will help you approach problems systematically and confidently.
Understanding key geometric concepts is not only important for solving problems but also for interpreting and visualizing spatial relationships. Familiarity with terms such as perimeter, area, volume, angles, and geometric properties allows you to approach questions with clarity and precision. Developing problem-solving strategies for geometric challenges will ensure that you can quickly apply the right methods and formulas during the test.
Essential Geometry Concepts to Focus On:
- Angles: Understand different types of angles (acute, right, obtuse) and how to calculate missing angles using properties like supplementary and complementary angles.
- Perimeter and Area: Master formulas for calculating the perimeter and area of basic shapes like rectangles, squares, triangles, and circles.
- Volume and Surface Area: Be comfortable calculating the volume and surface area of three-dimensional figures such as cubes, spheres, cylinders, and cones.
- Coordinate Geometry: Know how to plot points on a graph and apply the distance and midpoint formulas to find relationships between points.
- Triangles and Pythagorean Theorem: Understand how to apply the Pythagorean theorem to right triangles, and remember important properties of triangles like the sum of angles and special right triangles.
Key Formulas to Remember:
- Perimeter of a rectangle: P = 2(l + w)
- Area of a rectangle: A = l × w
- Volume of a cylinder: V = πr²h
- Pythagorean theorem: a² + b² = c² (for right triangles)
By mastering these geometry skills and practicing regularly with a variety of problems, you’ll be well-prepared to handle geometric questions efficiently. The key to success is not just memorizing formulas but understanding how and when to apply them in different scenarios. The more you practice, the more intuitive solving geometric problems will become.
Using a Calculator Effectively
In any test that involves numerical reasoning, knowing how to use a calculator efficiently is a key skill. The calculator is an essential tool that can help you save time and avoid errors, but only if you understand its functions and how to apply them effectively. Familiarizing yourself with its features before the test and practicing different calculations will ensure that you are prepared to handle any questions that require quick mathematical operations.
Many tests allow the use of calculators, but this doesn’t mean that relying on it should replace basic mathematical skills. Instead, it should complement your ability to solve problems more quickly and accurately. The trick is to know when to use the calculator and when to rely on mental calculations. Over-relying on a calculator can sometimes slow you down, especially if you’re not familiar with all its functions.
Tips for Maximizing Calculator Efficiency

- Familiarize Yourself with Key Functions: Before using the calculator during the test, ensure you understand the basic operations, memory functions, and how to access advanced features like square roots or percentages. This familiarity will save you valuable seconds when solving problems.
- Practice With Different Problems: Practice using your calculator on a variety of problems, including simple addition, subtraction, multiplication, and division, as well as more complex calculations such as fractions, percentages, and exponents. The more comfortable you are with the calculator, the more efficient you’ll be in the test.
- Use Parentheses Correctly: Many calculators allow you to input multiple operations in one line. Make sure to use parentheses to correctly organize complex expressions and avoid making mistakes in your calculations.
- Avoid Over-Reliance on the Calculator: While calculators are helpful, they should not replace your understanding of basic math principles. For example, if a problem involves simple arithmetic, try to perform the operation mentally first. Use the calculator for more complex steps or when time is running out.
Common Calculator Mistakes to Avoid
- Not Clearing Previous Entries: Always check that the display is clear before starting a new calculation. Some calculators retain previous operations, which can lead to incorrect results if you forget to reset them.
- Incorrect Input Order: Pay attention to the order of operations. If you’re unsure, use parentheses to explicitly define the correct order.
- Forgetting to Round: After performing calculations, ensure that you round the answers to the correct number of decimal places as required by the problem.
By mastering these calculator skills, you can use this tool to enhance your performance and efficiency. The key is practice: the more familiar you become with your calculator’s functions, the more confidently and accurately you will be able to solve problems during the test.
Reviewing Arithmetic and Basic Operations
Mastering fundamental arithmetic operations is the foundation for solving more complex numerical problems. These basic skills, which include addition, subtraction, multiplication, and division, are essential for tackling various types of questions. Having a solid grasp of these operations ensures accuracy and efficiency, especially when you are pressed for time during a test.
In addition to performing operations accurately, it’s important to understand how these operations interact with one another, such as the order in which they should be performed (known as the order of operations). This is crucial for avoiding common mistakes and solving problems correctly. Furthermore, having mental shortcuts or tricks for common calculations can save time and boost confidence during the test.
Key Arithmetic Skills to Review
- Addition and Subtraction: These are the most basic operations and form the foundation for more complex calculations. Be sure to practice adding and subtracting large numbers, fractions, and decimals.
- Multiplication and Division: These operations are often combined with other arithmetic skills in word problems. Review times tables, long division, and dividing fractions to improve accuracy.
- Understanding Fractions: Whether it’s simplifying fractions or converting them into decimals, having a strong understanding of how fractions work is essential. Review operations involving fractions such as addition, subtraction, multiplication, and division.
- Decimal Operations: Converting between decimals, fractions, and percentages is often required. Ensure you are comfortable adding, subtracting, multiplying, and dividing decimals.
Tips for Speed and Accuracy
- Practice Mental Math: Being able to perform basic calculations in your head without relying on a calculator can save precious time. Try to increase your mental math speed by practicing simple calculations regularly.
- Use Estimation: When a precise answer isn’t necessary, estimating the result can help you save time. For example, rounding numbers to the nearest ten or hundred can make calculations much faster.
- Check Your Work: Take a moment to review your calculations when possible. Even small errors in basic operations can lead to incorrect answers in more complex problems.
Common Pitfalls in Arithmetic Operations
| Common Error | Solution |
|---|---|
| Forgetting to carry over in addition | Double-check the addition process, especially with larger numbers, and remember to carry over when necessary. |
| Misplacing decimal points in multiplication/division | Ensure you correctly align decimals, especially when multiplying or dividing decimal numbers. |
| Confusing multiplication and division signs | Review the basic rules of multiplication and division, ensuring you follow them correctly. |
By honing your skills in these basic operations, you will significantly improve your ability to solve more advanced problems quickly and accurately. Consistent practice and a clear understanding of these concepts are key to mastering numerical reasoning.
Test-Taking Strategies for Math Success
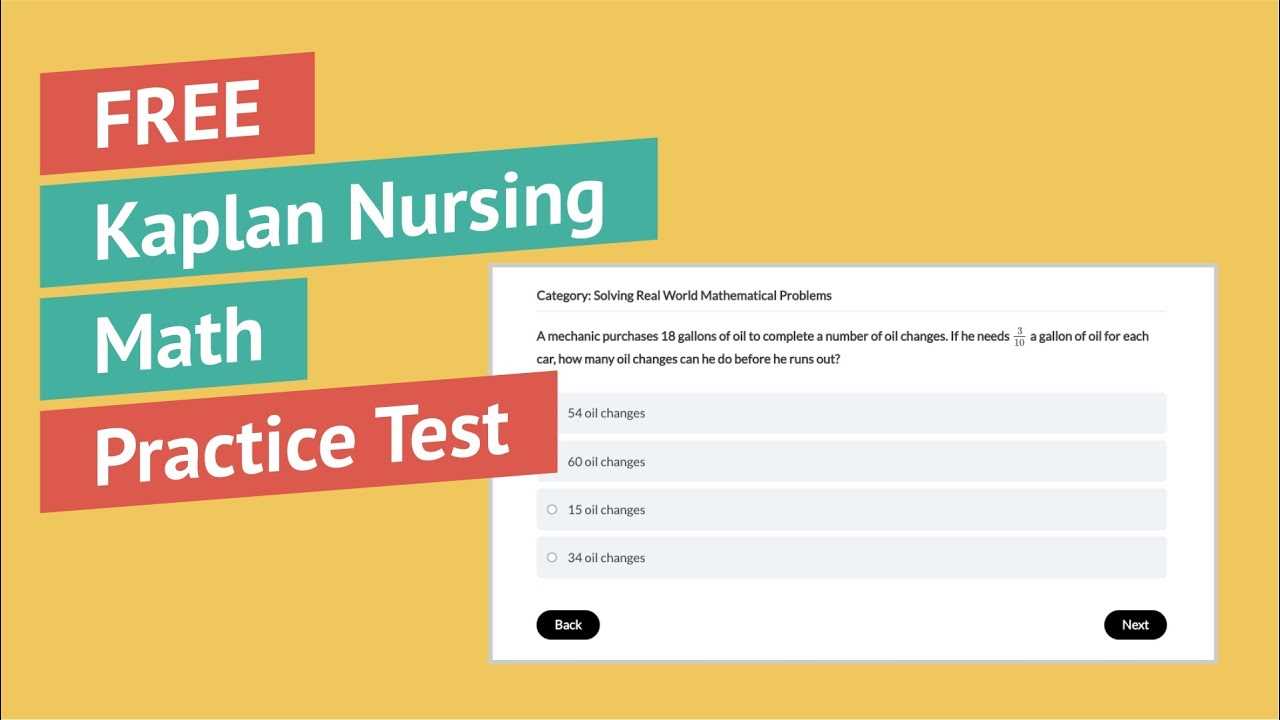
Approaching a test with a clear strategy is essential for maximizing performance, especially when dealing with complex numerical challenges. Effective test-taking strategies not only help you manage your time but also allow you to focus on solving problems more efficiently. By using the right techniques, you can reduce anxiety, avoid common mistakes, and enhance your overall test performance.
One of the key strategies is to carefully read each question and break it down step by step. This ensures you understand what is being asked and can apply the appropriate method to solve the problem. Additionally, managing your time wisely during the test can prevent rushed decisions and errors, allowing you to complete all questions with confidence.
Time Management During the Test
- Allocate Time Wisely: Before starting, quickly scan through the questions to get an idea of which ones may take more time. Allocate more time to complex problems and keep an eye on the clock to avoid spending too long on any single question.
- Work Efficiently: Aim to solve questions that you are confident in first, then revisit more difficult ones. This will give you a sense of accomplishment and reduce stress throughout the test.
- Skip and Return: If a question is taking too long, skip it and return to it later. This strategy ensures that you don’t lose valuable time on problems that might be difficult to crack under pressure.
Approaching Each Question with Confidence

- Read Carefully: Always read the instructions and questions carefully. Pay attention to keywords like “not,” “except,” or “all,” which can completely alter the meaning of the question.
- Break Down Complex Problems: For complicated questions, break the problem into smaller, manageable parts. Work through each part step by step, ensuring you don’t miss any crucial details.
- Use Process of Elimination: When unsure about an answer, eliminate clearly incorrect options first. This increases your chances of choosing the correct answer, even when guessing.
Maintaining Focus and Reducing Anxiety
- Stay Calm: Take deep breaths and stay calm, especially when you encounter difficult problems. Stress can lead to mistakes, so keeping a clear mind is essential.
- Don’t Rush: While time is limited, rushing through questions can lead to careless errors. Take your time, think carefully, and double-check your work when needed.
- Confidence is Key: Trust in your preparation and problem-solving abilities. Even if you encounter a challenging question, stay confident in your ability to tackle it.
By implementing these strategies, you can approach your test with a structured plan, helping you perform at your best and achieve your desired results. Consistent practice and a positive mindset are essential components of success, so take the time to refine your skills and strategies before the test day.
Common Mistakes to Avoid in Math
When tackling numerical challenges, it’s easy to make mistakes that can affect your performance. These errors often arise from carelessness, misunderstanding the problem, or rushing through questions. Recognizing and avoiding common pitfalls can improve accuracy and help you approach problems more effectively. By understanding the most frequent mistakes, you can be better prepared to avoid them during your assessment.
Overlooking Key Details

- Skipping Units: One of the most common mistakes is neglecting to check the units in a problem. Ensure that all quantities are in the same unit before performing calculations, as differences in units can lead to incorrect results.
- Misinterpreting the Question: Sometimes, rushing through the problem can cause you to misread or misunderstand what’s being asked. Always take a moment to re-read the question carefully and identify exactly what information is needed.
- Ignoring Negative Signs: Negative signs can easily be overlooked, especially when dealing with subtraction or division. Always double-check whether the operation requires a negative result.
Calculation Errors
- Simple Arithmetic Mistakes: Even the most basic operations can lead to errors when you’re under pressure. Always double-check your addition, subtraction, multiplication, and division steps to ensure accuracy.
- Incorrect Order of Operations: When solving multi-step problems, it’s important to follow the correct order of operations (PEMDAS: Parentheses, Exponents, Multiplication, Division, Addition, Subtraction). Skipping this crucial step can result in incorrect answers.
- Rounding Too Early: Rounding numbers prematurely during calculations can lead to inaccurate answers. It’s best to keep numbers in their full, unrounded form until the final step.
Time Management Mistakes
- Spending Too Much Time on One Problem: It’s easy to get stuck on a difficult problem, but spending too much time on it can cost you valuable minutes. If you’re unsure, move on to the next problem and come back later with a fresh perspective.
- Skipping Check for Reasonableness: After solving a problem, take a moment to check whether the result makes sense. An answer that seems too large or too small might indicate a miscalculation.
By being aware of these common errors, you can develop habits that will improve your problem-solving skills and reduce the likelihood of making costly mistakes. Consistent practice and careful attention to detail are key to achieving accuracy and success.
Analyzing Practice Test Results

Reviewing the results of practice assessments is a crucial step in preparing for any test. It provides valuable insights into your strengths and areas for improvement. By carefully analyzing your performance, you can identify patterns in the types of questions you struggle with, as well as the strategies that worked well. This process allows you to focus your efforts more effectively, ensuring better preparation for the real challenge.
Identifying Strengths
- Recognizing Proficiency: Pay attention to the sections or topics where you consistently perform well. These are your areas of strength, and it’s important to maintain confidence in these skills while reinforcing them further.
- Confirming Understanding: If you perform well in certain question types, it’s a sign that you have mastered the underlying concepts. This allows you to confidently move on to more complex problems or areas that need attention.
Spotting Weaknesses
- Targeting Specific Areas: Look for trends in the sections where you struggled. Were there specific concepts or types of questions that consistently caused difficulty? Identifying these areas will allow you to concentrate your study efforts where they are most needed.
- Analyzing Mistakes: Take note of the questions you got wrong and understand why you made those errors. Was it a simple mistake or a misunderstanding of the concept? This reflection will help you avoid similar mistakes in the future.
- Time Management Issues: Sometimes, struggles arise from not managing time effectively. Review how long it took to answer each question–if you spent too much time on certain problems, practice improving your pace to avoid getting stuck on difficult questions during the real test.
By reviewing your practice test results with a critical eye, you can make data-driven decisions about how to adjust your study plan. This focused approach will help maximize your preparation and boost your confidence as you approach your goal.
Final Review Before the Test
As the test date approaches, a final review is essential to consolidate your knowledge and ensure you’re fully prepared. This last round of studying should focus on reinforcing key concepts, addressing any lingering uncertainties, and boosting your confidence. The goal is to refresh your memory, refine your problem-solving strategies, and ensure that you’re able to tackle any challenge that comes your way during the test.
Start by reviewing the most important topics and any areas where you may have struggled in practice tests. It’s helpful to revisit fundamental concepts that serve as the foundation for more complex problems. Practicing problems from different categories will also help you become more comfortable with the format and ensure you’re ready for any question type.
Key Focus Areas
- Core Concepts: Revisit the fundamental operations, such as addition, subtraction, multiplication, and division, as these are the building blocks for more advanced topics.
- Common Formulas: Make sure you’re familiar with important formulas, including those for percentages, ratios, and geometric calculations. These are often essential in solving specific types of problems efficiently.
- Problem-Solving Strategies: Reinforce your approach to solving different problem types. Whether it’s algebraic equations, word problems, or data interpretation, practicing with varied questions will help solidify your understanding.
Test-Taking Strategies
- Time Management: Make sure you’re aware of the time constraints. Practice pacing yourself to ensure you can complete all questions within the allotted time without rushing.
- Staying Calm: Test anxiety can affect your performance. Practice mindfulness techniques or deep breathing to remain calm and focused during the test.
- Eliminating Answers: If you encounter a difficult question, use the process of elimination to narrow down the options. Often, eliminating one or two incorrect answers increases your chances of selecting the right one.
With this final review, you’ll feel more confident and better equipped to perform at your best. Take the time to carefully go over the material, practice key problem types, and refresh your strategies. The more prepared you are, the more likely you are to succeed when it’s time to take the test.