
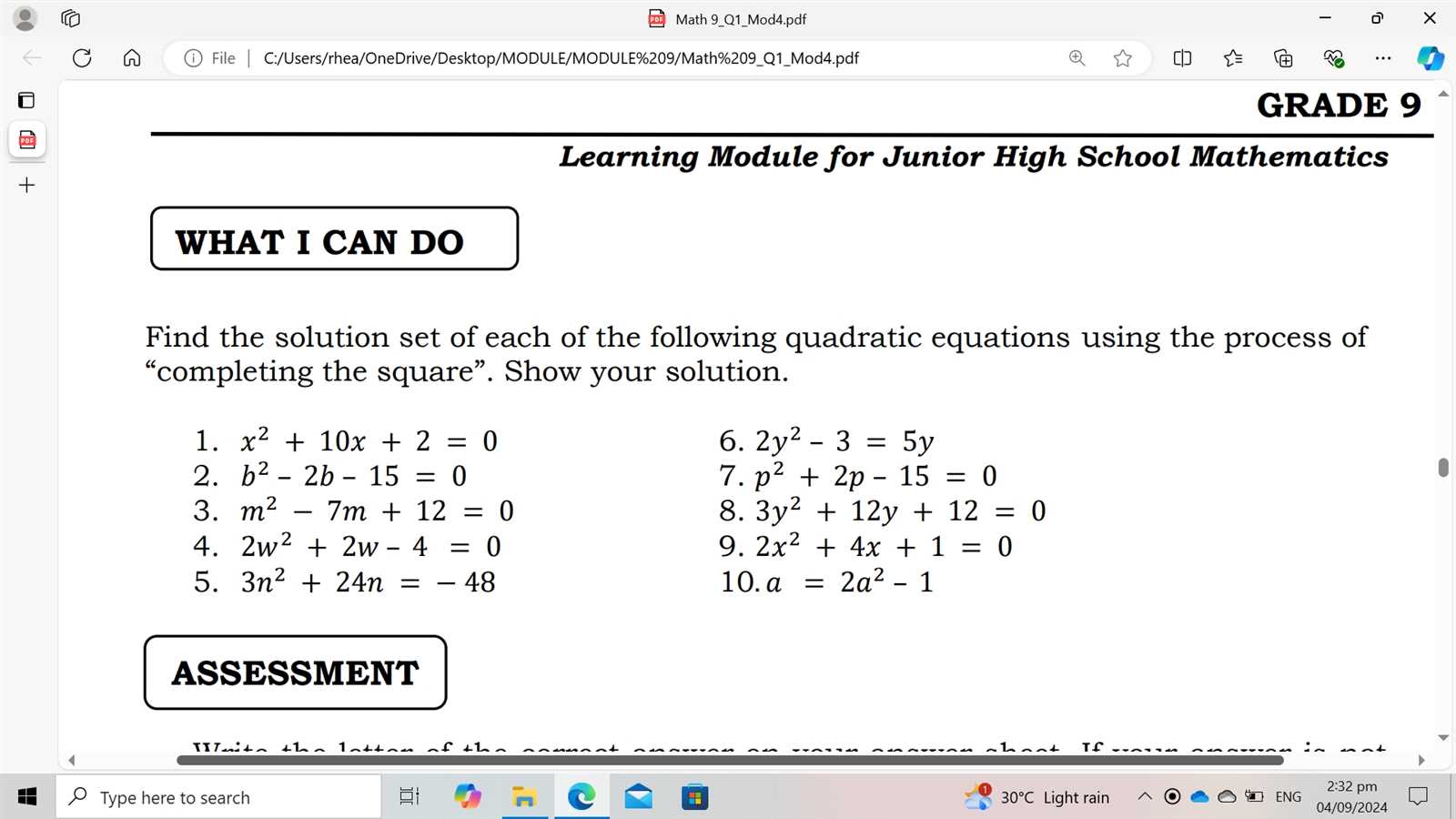
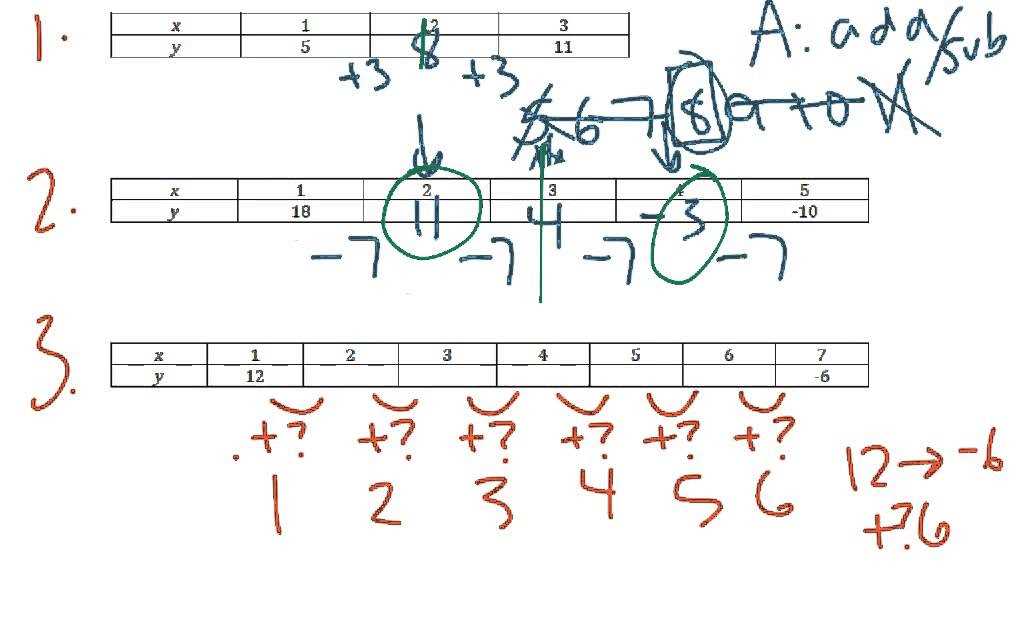
In this section, we focus on enhancing your understanding of essential topics in the early stages of your studies. The goal is to break down complex problems and present clear, step-by-step solutions that help build a strong foundation. By mastering these concepts, you’ll gain confidence and improve your ability to solve challenges independently.
With the right approach and practice, you can easily grasp the necessary techniques to tackle various tasks. We emphasize critical skills, such as problem-solving strategies, logic, and comprehension, ensuring that you’re well-equipped to move forward. Each solution is designed to provide clarity, ensuring that every step is understandable and actionable.
Through this guide, you’ll find practical methods for improving your skills. Whether it’s tackling numerical problems or applying theoretical knowledge, the emphasis is on developing a solid understanding and practical expertise. Stay focused and practice regularly, and you’ll see your abilities grow.
Understanding Secondary Math 1 Module 2
This section explores the foundational principles and techniques that are essential for mastering the core topics. The focus is on developing a deeper understanding of mathematical reasoning, improving problem-solving skills, and applying learned strategies effectively. By breaking down complex tasks into manageable steps, this guide helps learners approach challenges with confidence.
Clarity and simplicity are key when tackling these concepts. Instead of memorizing formulas, the goal is to understand how they are derived and when to apply them. This approach enhances critical thinking and ensures that learners not only perform well on assessments but also grasp the underlying logic that governs each topic.
Each section of this material is designed to build upon previous knowledge, reinforcing skills as new topics are introduced. By following the structured steps and practicing regularly, learners will develop both proficiency and confidence in handling increasingly advanced challenges.
Key Concepts of Module 2 Math

This section focuses on the essential principles that form the foundation of advanced problem-solving. Understanding these core ideas is crucial for progressing in your studies and applying concepts effectively in various contexts. By mastering these concepts, learners can approach complex challenges with a clear understanding and enhanced skills.
Among the key topics covered are various methods of solving equations, working with geometric shapes, and exploring relationships between variables. Each concept is introduced gradually, ensuring a strong grasp of the material before advancing to more complex ideas. This approach allows learners to not only perform calculations but also understand the logic and reasoning behind them.
By developing a deeper understanding of these fundamental ideas, students are better equipped to tackle real-world problems and further mathematical concepts in future lessons. The emphasis is on clarity, practice, and application, all of which are vital for achieving long-term success in your studies.
Step-by-Step Solutions for Exercises
This section provides detailed solutions to key exercises, broken down into clear, manageable steps. The goal is to guide learners through the process of solving each problem, ensuring they understand every stage of the solution. By following these step-by-step instructions, students can develop the confidence and skills needed to approach similar challenges independently.
Each solution is carefully explained, highlighting the methods and techniques used at every step. This approach not only clarifies the process but also reinforces the underlying concepts that are essential for solving similar problems in the future. The emphasis is on understanding the logic behind each step rather than simply memorizing procedures.
As you work through these exercises, take the time to carefully follow each step and reflect on why each method is used. Practice and repetition are key to mastering these techniques, and with consistent effort, students can improve both their problem-solving ability and their overall understanding of the material.
How to Approach Problems Effectively
Understanding how to tackle challenges efficiently is crucial for achieving success. The key is to break down the problem into smaller, more manageable parts, allowing you to address each aspect individually. This method not only simplifies complex tasks but also enhances problem-solving skills by focusing on one step at a time.
Start by carefully analyzing the problem to understand what is being asked. Identify the known information and the variables that need to be determined. Once you have a clear understanding, choose an appropriate strategy or technique that will help solve the problem. This structured approach ensures that you stay organized and focused throughout the process.
Additionally, practice is essential. The more you familiarize yourself with different types of problems, the better you’ll become at identifying the most effective methods for solving them. By applying these strategies consistently, you’ll improve both your speed and accuracy in handling similar tasks in the future.
Common Mistakes in Secondary Math 1
In any learning process, errors are a natural part of development. However, recognizing and understanding common mistakes can help avoid repeating them. Identifying these pitfalls early allows learners to correct them and build stronger problem-solving skills.
Typical Errors in Problem Solving

Many students make similar mistakes when working through exercises. These errors often stem from misunderstandings of core concepts or rushing through steps without proper consideration. Below are some common mistakes to watch out for:
- Skipping Steps: Failing to break the problem into smaller parts can lead to missed information or incorrect results.
- Misinterpreting the Question: Not fully understanding the problem can result in applying the wrong methods or strategies.
- Overlooking Negative Signs: Neglecting negative numbers, especially when dealing with equations or operations, can lead to incorrect answers.
- Incorrect Application of Formulas: Using the wrong formula or misunderstanding how to apply it often results in mistakes.
How to Avoid These Mistakes
By being aware of these common pitfalls, learners can take steps to prevent them. Carefully reading each problem, taking time to review each step, and double-checking calculations are all essential habits to develop.
- Review Work Thoroughly: Always check each solution for possible errors before finalizing the answer.
- Understand the Concepts: Strengthen the understanding of foundational principles to avoid confusion during problem-solving.
- Practice Consistently: Regular practice helps reinforce correct methods and reduces the likelihood of making errors.
Tips for Mastering Math Module 2
Achieving proficiency in this part of your studies requires focus, practice, and the right strategies. To master the content effectively, it’s important to approach each topic with a clear plan and a structured method. Here are some key tips that will help you navigate the challenges and succeed in mastering the material.
| Tip | Description |
|---|---|
| Break Down Complex Problems | Divide challenging tasks into smaller, more manageable steps to avoid feeling overwhelmed and to ensure a clearer path to the solution. |
| Practice Regularly | Consistent practice is essential for reinforcing concepts and improving problem-solving skills over time. |
| Seek Understanding, Not Memorization | Rather than memorizing formulas, focus on understanding the logic behind them, which will help in applying them correctly in different scenarios. |
| Review Your Mistakes | After completing exercises, go back and carefully review any mistakes to understand where things went wrong and how to improve. |
| Ask Questions | Don’t hesitate to ask for help when you’re stuck. Clarifying doubts early prevents confusion later on. |
By following these tips and staying consistent, you’ll build a solid foundation and be well-equipped to tackle even the most challenging problems. Remember, mastery comes with time and dedicated effort.
Importance of Practice in Math Learning
Mastery in any subject requires continuous practice, and this is especially true when it comes to numerical and problem-solving skills. Regularly practicing concepts not only reinforces your understanding but also helps you develop the confidence to tackle increasingly difficult challenges. The more you engage with the material, the more intuitive the solutions will become.
How Practice Enhances Learning
Consistent practice brings several benefits. It helps solidify concepts, making them easier to recall when needed. Additionally, it allows you to identify patterns and recognize common strategies for solving problems. As a result, practice doesn’t just improve your ability to complete exercises; it strengthens your overall understanding of the material.
| Benefit | Explanation |
|---|---|
| Improved Retention | Regular practice ensures that the material stays fresh in your memory, making it easier to recall during tests or real-world applications. |
| Increased Speed | Repetition helps build speed and efficiency, allowing you to solve problems more quickly and accurately over time. |
| Better Problem-Solving Skills | Frequent engagement with exercises helps you learn how to approach problems from different angles, improving critical thinking. |
| Boosted Confidence | As you practice more, you’ll feel more confident in your abilities, which helps reduce anxiety during exams and assignments. |
Tips for Effective Practice
To make the most out of your practice sessions, it’s important to stay focused and consistent. Set aside dedicated time each day for reviewing and solving problems. Mix up different types of exercises to ensure you’re not just repeating the same process but are also strengthening various aspects of your skills.
Explaining Core Math Principles Clearly
Understanding the foundational concepts is key to mastering any subject. When learning complex topics, it’s crucial to break down the core principles in a way that makes them easy to understand. A clear explanation of basic ideas not only helps in solving problems but also builds a strong foundation for tackling more advanced concepts later on.
One of the most effective ways to explain fundamental concepts is by using simple language and relatable examples. Avoiding jargon and focusing on the core idea allows students to grasp the essence of the topic without feeling overwhelmed. Additionally, breaking down each concept into smaller steps ensures that learners can follow the logic and apply the principles accurately.
By focusing on clarity and simplicity, students can develop a deeper understanding of the material, which enables them to approach more challenging problems with greater ease and confidence.
Solving Word Problems with Ease

Word problems can often seem intimidating, but with the right approach, they can be solved efficiently and accurately. The key to tackling these challenges is to break down the information and focus on the steps required to find the solution. By following a structured process, you can transform a complex word problem into a manageable task.
Step-by-Step Approach
Start by carefully reading the problem and identifying the important details. It is essential to understand what is being asked and what information is given. Once you’ve identified the key elements, translate them into mathematical terms or operations. This could mean recognizing numbers, relationships, or conditions that need to be applied to solve the problem.
Organize Your Work
As you begin solving the problem, keep your work organized. Write down each step, clearly showing how you arrived at the next point. This method helps prevent errors and makes it easier to check your work. Additionally, drawing diagrams or using tables can help visualize the problem and clarify the relationships between the variables.
By staying organized and focused on the logical steps, you can tackle word problems with confidence, ensuring a more systematic and efficient approach to solving them.
Understanding Fractions and Decimals
Both fractions and decimals are ways of expressing parts of a whole, and mastering these concepts is essential for progressing in problem-solving tasks. While they represent the same idea of division, their formats can often lead to confusion. However, with a solid understanding of both, converting between them and solving related problems becomes straightforward.
Fractions: Breaking Down Parts
A fraction is a way to represent a part of a whole by dividing it into equal parts. The top number, known as the numerator, shows how many parts are being considered, while the bottom number, the denominator, indicates how many equal parts make up the whole. Understanding this division is fundamental to grasping the relationship between numbers and working with them in different problems.
Decimals: A Different Viewpoint

Decimals are another method for representing parts of a whole, but instead of using a numerator and denominator, they use a place value system. Each digit in a decimal number has a specific place value, such as tenths, hundredths, and thousandths, based on its position relative to the decimal point. Recognizing how decimals correspond to fractions helps in converting between these two formats with ease.
Both fractions and decimals are crucial tools in mathematics, and developing a strong understanding of how they relate to one another and how to work with them will aid in solving a variety of numerical challenges.
Algebraic Techniques in Module 2
In algebra, understanding the core techniques used to manipulate and solve equations is essential for success in any problem-solving scenario. These techniques are designed to simplify complex expressions and help uncover unknown values. By mastering these foundational methods, students can tackle a wide variety of problems with confidence and accuracy.
There are several key algebraic techniques that are frequently applied in exercises. These methods not only aid in simplifying equations but also lay the groundwork for more advanced concepts in later studies.
Common Algebraic Techniques
- Simplifying Expressions: Combine like terms to reduce expressions to their simplest form.
- Solving Linear Equations: Use addition, subtraction, multiplication, and division to isolate variables and solve for unknowns.
- Factoring: Decompose expressions into simpler factors that can be more easily manipulated or solved.
- Distributive Property: Apply the distributive property to expand or simplify expressions involving multiplication over addition or subtraction.
- Working with Inequalities: Understand how to manipulate and solve inequalities by following similar steps to those used in equations.
Each of these techniques plays a crucial role in solving algebraic problems and offers a systematic way to approach more complex tasks. By practicing these methods, students can become proficient at handling a variety of algebraic challenges efficiently.
Geometry Topics Covered in Module 2
Geometry is a key area of study that involves understanding shapes, sizes, and the properties of space. In this section, a variety of geometric concepts are introduced and explored in depth. By mastering these topics, students gain the ability to analyze and solve problems related to space and form. Understanding these core principles is essential for progressing in more advanced mathematical concepts and applications.
Core Geometry Topics
- Angles: Identifying different types of angles (acute, right, obtuse) and understanding their properties and relationships.
- Lines and Line Segments: Exploring the properties of parallel, perpendicular, and intersecting lines, as well as the concept of line segments.
- Triangles: Investigating various types of triangles (equilateral, isosceles, scalene) and their properties, including angles and side lengths.
- Perimeter and Area: Calculating the perimeter and area of basic geometric shapes such as squares, rectangles, and triangles.
- Circles: Understanding the basic properties of circles, including radius, diameter, and circumference, and how to calculate their area.
Geometric Applications
- Real-world Problem Solving: Applying geometric principles to solve practical problems in architecture, engineering, and design.
- Proportions and Ratios: Using geometric principles to understand proportions, ratios, and scale factors in various contexts.
These geometry topics provide a solid foundation for further study and help students develop critical thinking skills needed to approach more complex problems in mathematics and beyond.
Real-Life Applications of Module 2 Math
The concepts learned in this section of mathematics extend far beyond the classroom and play a crucial role in various aspects of everyday life. Whether you’re budgeting, designing a structure, or planning a trip, the skills developed here are practical tools used to solve real-world problems. Understanding how these concepts apply to daily activities makes learning more relevant and shows their importance in a wide range of fields.
Practical Uses in Everyday Life
- Personal Finance: Calculating budgets, determining expenses, and understanding percentages are all made easier with the skills gained from these topics.
- Home Design: Whether you’re rearranging furniture, designing a garden, or building a structure, knowledge of geometry and measurements is essential for creating accurate and functional layouts.
- Cooking and Recipes: Fractions and ratios are used regularly when adjusting ingredients or scaling recipes up or down for different serving sizes.
- Travel Planning: Estimating travel time, calculating distances, and understanding maps require a solid understanding of geometry, proportions, and basic arithmetic.
Applications in Professional Fields
- Architecture and Engineering: Design and construction of buildings, bridges, and roads rely heavily on geometric principles to ensure safety, stability, and functionality.
- Technology and Design: Professionals in fields like graphic design and computer programming use algebraic concepts to create algorithms, solve problems, and optimize solutions.
- Medicine: Medical professionals use mathematics in various ways, such as calculating dosages, interpreting test results, and analyzing statistical data for medical studies.
These examples show how the principles learned in this section of mathematics help solve practical problems in both personal and professional settings. By connecting abstract concepts to real-life applications, students gain a deeper appreciation for the relevance of mathematics in their everyday lives.
Reviewing Key Formulas and Theorems

Understanding the fundamental formulas and theorems in mathematics is essential for solving complex problems efficiently. In this section, we will review some of the most important equations and principles that form the foundation for various mathematical concepts. These formulas are not only crucial for solving academic problems but also have widespread applications in real-world scenarios.
Essential Formulas
- Area of a Rectangle: The area is calculated by multiplying the length by the width: Area = length × width.
- Perimeter of a Rectangle: The perimeter is the sum of all sides: Perimeter = 2 × (length + width).
- Area of a Triangle: The area is calculated by multiplying the base by the height and dividing by 2: Area = 1/2 × base × height.
- Volume of a Rectangular Prism: The volume is found by multiplying length, width, and height: Volume = length × width × height.
- Circumference of a Circle: The circumference is calculated by multiplying the diameter by π: Circumference = π × diameter.
Key Theorems
- Pythagorean Theorem: This theorem states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides: c² = a² + b².
- Properties of Angles: The sum of the interior angles of a triangle is always 180°, and the sum of the angles around a point is 360°.
- Distributive Property: This property allows us to multiply a number by a sum or difference: a × (b + c) = a × b + a × c.
Reviewing these key formulas and theorems is vital for reinforcing your understanding of core concepts and developing the ability to apply them in problem-solving scenarios. Mastery of these essential equations forms the basis for success in more advanced mathematical challenges.
Resources for Further Math Learning
To deepen your understanding of mathematical concepts and continue developing problem-solving skills, there are numerous resources available. These tools can help clarify difficult topics, provide additional practice, and offer insights into more advanced areas of study. Whether you’re looking for interactive platforms, comprehensive textbooks, or video tutorials, there is something to suit every learning style.
- Online Courses: Websites like Khan Academy, Coursera, and edX offer free and paid courses that cover a wide range of mathematical topics. These platforms provide video lessons, quizzes, and interactive exercises that help reinforce learning.
- Textbooks and Guides: Comprehensive books such as “Algebra for Dummies” or “Geometry Essentials” can offer in-depth explanations and practice problems. These resources often include step-by-step solutions to help clarify complex concepts.
- Interactive Learning Platforms: Websites like Desmos and GeoGebra allow you to visualize mathematical functions and geometric shapes, helping to build a deeper understanding through hands-on exploration.
- YouTube Channels: Channels like PatrickJMT and 3Blue1Brown provide clear explanations of mathematical principles through engaging videos that break down complex ideas into digestible pieces.
- Study Groups and Forums: Joining online communities such as Stack Exchange or Reddit’s r/learnmath can provide additional support. You can ask questions, collaborate with others, and gain insights from peers and experts.
By utilizing these resources, you can continue to build a strong foundation in mathematics, preparing for future challenges and expanding your knowledge in various areas. Regular practice and exposure to different teaching methods are key to mastering the subject and applying it effectively in real-world situations.
Time Management for Math Study
Effective time management is crucial when it comes to mastering mathematical concepts. Allocating enough time for studying, practicing, and reviewing key ideas can make all the difference in achieving success. Properly managing your study time ensures that you can cover all necessary material without feeling overwhelmed, while also allowing time for reflection and revision.
To optimize your study sessions, it’s important to create a structured plan that balances focused study time with breaks. This approach not only helps maintain concentration but also prevents burnout. Breaking down complex topics into manageable sections can make learning more efficient and less daunting.
Key Strategies for Efficient Time Use
- Set Clear Goals: Define specific, measurable objectives for each session, such as mastering a particular concept or solving a set number of problems. This helps maintain focus and track progress.
- Prioritize Difficult Areas: Spend extra time on challenging topics. Tackle the most difficult problems early in the study session when your energy levels are highest.
- Use a Timer: Try the Pomodoro Technique or similar time management methods. Work for 25 minutes, then take a 5-minute break. This keeps you fresh and focused throughout the study period.
- Review Regularly: Allocate time for regular review sessions, even if it’s just a few minutes each day. Consistent reinforcement helps solidify long-term retention.
With consistent effort and well-planned study time, you can gradually improve your understanding and performance in mathematical tasks. Keep track of your progress and adjust your study routine as needed to stay on top of new topics while reinforcing previously learned material.
Building Confidence in Math Skills
Developing confidence in mathematical abilities is essential for long-term success. When students believe in their capacity to solve problems, they approach challenges with a positive mindset, which leads to better learning outcomes. Confidence isn’t built overnight; it requires consistent practice, reflection, and the right strategies to overcome obstacles.
A key factor in boosting confidence is mastering foundational concepts before tackling more complex topics. Start by understanding the basic principles thoroughly, as this provides a solid framework for solving more advanced problems. As you build a strong base, the more intricate concepts will start to make sense, and this gradual progression helps reinforce self-assurance.
Effective Strategies for Confidence Building
- Practice Regularly: The more you practice, the more confident you become in solving problems. Start with simpler exercises and gradually increase difficulty as your comfort grows.
- Celebrate Small Wins: Acknowledge each success, no matter how small. Recognizing progress helps reinforce the belief that you are capable of achieving more.
- Learn from Mistakes: Mistakes are a natural part of the learning process. Rather than feeling discouraged, use errors as opportunities for growth and understanding. Review where you went wrong and approach the problem from a different angle.
- Seek Support When Needed: Don’t hesitate to ask for help. Whether from a teacher, a classmate, or online resources, getting support can clarify difficult concepts and boost your confidence.
By focusing on steady progress and maintaining a positive attitude, you can significantly increase your confidence in handling mathematical problems. Remember, every step forward–no matter how small–contributes to a stronger foundation and a more confident approach to learning.