
Preparing for an important assessment can be a challenging task, but with the right approach, you can tackle the material with confidence. Understanding the core principles and applying effective problem-solving techniques is crucial for success. This guide will provide you with the essential tools to navigate your upcoming evaluation with ease.
Key concepts such as probability, data interpretation, and hypothesis testing form the foundation of many questions. Mastering these areas will help you answer both simple and complex queries accurately. Knowing how to approach each type of problem is just as important as memorizing formulas and definitions.
In the following sections, you will find tips and strategies to prepare effectively. From time management during the test to understanding various statistical models, each piece of advice is designed to enhance your performance and boost your confidence.
Essential Tips for Business Stats Exam

When preparing for an important test in this field, it’s crucial to focus on mastering both theoretical concepts and practical problem-solving techniques. Whether you’re handling formulas, interpreting data, or analyzing trends, the ability to quickly apply your knowledge under pressure can make a significant difference. This section will guide you through key strategies to enhance your preparation and improve your performance.
Understand Core Principles
Having a strong grasp of foundational topics is essential. Key concepts such as probability, data distribution, and regression analysis frequently appear in assessments. Rather than simply memorizing formulas, focus on understanding how these concepts apply to real-world situations. Practice solving problems from various angles to strengthen your comprehension.
Practice with Real-Life Data
Working with actual datasets and applying the learned methods helps bridge the gap between theory and practice. Try to solve problems that require you to draw conclusions based on presented data. Familiarize yourself with how to use spreadsheets or software tools to assist in analyzing and interpreting information. The more you practice, the more confident you will feel during the test.
| Concept | Tip |
|---|---|
| Data Interpretation | Focus on reading and understanding charts and graphs, paying close attention to trends and outliers. |
| Probability | Start with simple probability questions to build your confidence, then progress to more complex scenarios. |
| Regression | Practice identifying variables and using them to predict outcomes effectively. |
By focusing on these tips, you’ll be better equipped to approach the test with confidence. Remember, a thorough understanding combined with consistent practice is the key to success.
Understanding Key Statistical Concepts
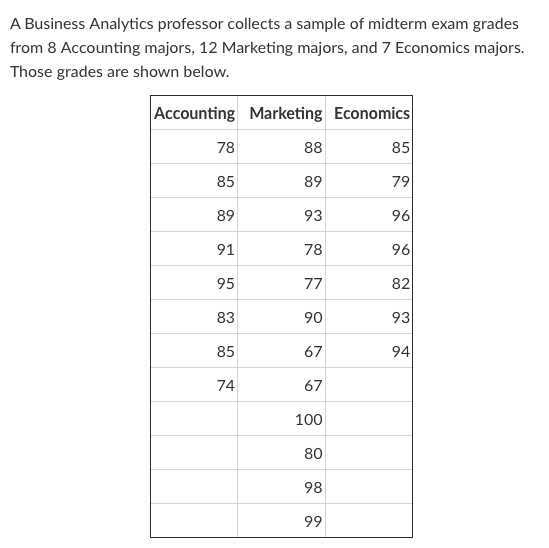
A strong foundation in core principles is essential for tackling any test in this area. The ability to comprehend and apply fundamental concepts will not only help you solve problems effectively but also enhance your ability to interpret real-world data. This section covers essential topics that you must master in order to perform well and understand how they are interconnected.
Key Variables and Their Relationships
Understanding the relationship between different variables is crucial for making accurate predictions and interpretations. Concepts such as independent and dependent variables allow you to break down complex problems and focus on the factors that matter most. Recognizing how these variables interact in various models will give you a deeper insight into the data.
Commonly Used Models and Formulas
Another important aspect of mastering this field is getting familiar with various models and formulas that are widely used. Linear regression is a fundamental technique that helps predict outcomes, while probability distributions allow you to understand the likelihood of events. Ensure you are comfortable with calculating key measures like mean, median, and standard deviation as they are integral to solving many types of problems.
By grasping these core ideas, you’ll have the tools necessary to tackle a wide range of challenges confidently and accurately.
How to Solve Probability Problems
Solving probability-related challenges requires a clear understanding of basic principles and the ability to apply them to different scenarios. Whether you’re determining the likelihood of a single event or analyzing multiple outcomes, following a structured approach will help you navigate through the calculations and make accurate predictions. In this section, we’ll outline the essential steps to solving probability problems efficiently.
Steps for Solving Probability Problems
To solve probability questions, it’s important to break down the problem into manageable steps. The following approach will guide you through the process:
- Identify the Event: Determine what you’re trying to calculate the probability for, whether it’s a single event or a set of events.
- Count the Total Outcomes: List all possible outcomes in the sample space. This will form the denominator in your probability calculation.
- Count the Favorable Outcomes: Identify the outcomes that align with the event you’re analyzing, which will form the numerator.
- Calculate the Probability: Use the formula: Probability = (Favorable Outcomes) / (Total Outcomes).
Common Probability Techniques

Different types of probability problems require distinct methods for solving them. Below are some common techniques:
- Simple Probability: Used for single events, where you calculate the likelihood of one outcome occurring.
- Conditional Probability: Involves finding the probability of an event given that another event has already occurred.
- Combinations and Permutations: Helpful when dealing with problems involving multiple events or selections from a group.
With practice and a solid understanding of these methods, you’ll be well-equipped to solve even the most complex probability problems.
Interpreting Data and Graphs Effectively
Interpreting data and visual representations accurately is a critical skill for making informed decisions. Whether you’re analyzing numerical values, trends, or relationships between variables, understanding how to read and interpret various types of data visualizations is key. In this section, we’ll explore effective techniques for interpreting graphs and datasets to extract meaningful insights.
When working with graphs, it’s essential to pay attention to key elements like the axis labels, scale, and legends. These components provide important context and help you understand what the graph is representing. Additionally, recognizing patterns such as trends, outliers, and correlations allows you to draw accurate conclusions from the data.
Common Graph Types and How to Read Them
Graphs come in various forms, each designed to present data in specific ways. Below are some of the most common graph types and key points to keep in mind when interpreting them:
| Graph Type | What to Look For |
|---|---|
| Bar Graph | Compare categories, look for trends in height or length, and identify the relative size of each category. |
| Line Graph | Track changes over time, identify trends, and detect any patterns of increase or decrease. |
| Pie Chart | Assess proportions of a whole, identify the largest and smallest segments, and look for imbalances. |
By familiarizing yourself with these graph types and practicing interpretation, you’ll become more proficient in understanding complex datasets and visual representations.
Common Mistakes to Avoid in Exams
During an important test, it’s easy to make errors that can significantly affect your score. Many of these mistakes stem from a lack of preparation, poor time management, or simply misunderstanding the question. This section will highlight some of the most common pitfalls students encounter and offer practical advice on how to avoid them.
One of the most frequent mistakes is rushing through questions without fully understanding them. It’s important to carefully read each problem and ensure you grasp what is being asked before attempting a solution. Another common issue is misapplying formulas or methods, often due to a lack of thorough practice. Understanding when and how to use specific techniques is essential for accurate results.
Finally, overlooking small details, such as ignoring units or incorrectly interpreting a graph, can lead to errors that would otherwise be easy to avoid. Paying attention to every aspect of the problem, even the seemingly minor ones, is crucial for success.
Time Management During the Exam
Effective time management is one of the most important skills to master when preparing for and taking a test. Allocating the right amount of time to each section of the test, while ensuring you don’t rush through any part, can make a huge difference in your overall performance. This section focuses on strategies to help you manage your time efficiently during the assessment.
Prioritize the Questions
One of the first things to do when you receive the test is to quickly scan through all the questions. Identify which ones you feel most confident about and can answer quickly. These should be tackled first to build momentum. Save the more challenging or time-consuming questions for later when you have more time to focus on them.
Allocate Time for Each Section
Before you begin, set a time limit for each section or set of questions based on their point value and complexity. Use a watch or the timer provided to keep track of time, ensuring that you don’t spend too long on any single part. If a question is taking too long, move on and come back to it later if time permits.
By carefully managing your time, you can ensure that you have the opportunity to attempt every question while giving yourself enough time to review your answers before finishing.
How to Approach Hypothesis Testing
Hypothesis testing is a fundamental process used to make inferences or draw conclusions from data. It involves evaluating whether there is enough evidence to support or reject a proposed claim about a population based on a sample. This section will guide you through the essential steps to approach hypothesis testing methodically and accurately.
Steps to Conduct Hypothesis Testing
When tackling a hypothesis testing question, follow these systematic steps:
- State the Hypotheses: Begin by formulating the null hypothesis (H0) and the alternative hypothesis (Ha). The null hypothesis generally represents a position of no effect or no difference, while the alternative hypothesis suggests a possible effect or difference.
- Choose the Significance Level: Select an appropriate significance level (alpha), commonly 0.05, which determines the threshold for rejecting the null hypothesis.
- Select the Test: Choose the right statistical test based on the type of data and the hypotheses being tested, such as a t-test, z-test, or chi-square test.
- Calculate the Test Statistic: Use the relevant formula to compute the test statistic, which will help assess whether the sample data falls within the expected range.
- Make a Decision: Compare the test statistic to the critical value or use the p-value to determine whether to reject or fail to reject the null hypothesis.
- Draw a Conclusion: Based on the decision, conclude whether there is sufficient evidence to support the alternative hypothesis or if the null hypothesis stands.
Common Pitfalls to Avoid
- Misinterpreting p-values: A p-value below the chosen significance level indicates strong evidence against the null hypothesis. A common mistake is to assume a p-value represents the probability that the null hypothesis is true.
- Ignoring Assumptions: Every test has assumptions (e.g., normality, independence) that must be met for valid results. Failing to check these assumptions can lead to misleading conclusions.
- Overlooking Sample Size: Small sample sizes can lead to unreliable results, especially when testing for small effects. Ensure your sample size is large enough to detect meaningful differences.
By following these steps and avoiding common errors, you can approach hypothesis testing with confidence and accuracy, ensuring valid conclusions based on your data.
Critical Formulas You Must Know
Mastering key formulas is essential for solving many types of problems in quantitative analysis. These formulas are the foundation of the calculations you’ll need to perform, whether you’re analyzing data or testing hypotheses. This section highlights the most important formulas you should be familiar with and provides a clear understanding of how and when to apply them.
First, it’s crucial to understand the formula for calculating the mean, which represents the average value of a dataset. Similarly, knowing how to compute the variance and standard deviation helps quantify the spread or dispersion of data points. Other critical formulas include those for confidence intervals, probability distributions, and regression analysis, all of which are frequently used in data interpretation.
Key Formulas
Here are some essential formulas to know:
- Mean (Average): μ = (ΣX) / N
Where μ is the mean, ΣX is the sum of all data points, and N is the total number of data points.
- Variance: σ² = (Σ(X – μ)²) / N
Variance measures the spread of data points from the mean.
- Standard Deviation: σ = √(σ²)
The square root of the variance, it provides a more intuitive measure of spread.
- Confidence Interval: CI = X̄ ± Z * (σ / √n)
Used to estimate a range within which the population parameter lies, based on sample data.
- Linear Regression Equation: y = mx + b
This equation models the relationship between two variables, where m is the slope and b is the y-intercept.
These formulas are fundamental tools for performing various calculations and analyzing data. Having them readily available and understanding their application will greatly enhance your ability to solve problems efficiently and accurately.
Practical Examples for Midterm Preparation
Preparing for a significant test requires more than just reviewing concepts; it involves applying what you’ve learned to real-world problems. Practical examples help bridge the gap between theory and practice, allowing you to better understand how to use your knowledge in different scenarios. This section will provide a variety of examples that will assist in reinforcing your skills and enhancing your readiness for the upcoming assessment.
To effectively prepare, it’s essential to work through different types of problems. Practice questions not only help familiarize you with the format but also help you identify common patterns in problem-solving. By applying the techniques and formulas you’ve learned, you will develop a deeper understanding of how to approach similar problems in the test.
Example 1: Calculating the Average

Suppose you are given a dataset representing the monthly sales of a store over the past year. To find the average sales, you would sum all the sales values and divide by the number of months. The formula is:
Mean = (Sum of all sales values) / Number of months
By practicing with this type of problem, you’ll become more comfortable with basic calculations and learn how to interpret the results.
Example 2: Hypothesis Testing
Imagine you’re tasked with testing whether a new marketing campaign has improved sales. You would set up a null hypothesis stating that the campaign has no effect, and an alternative hypothesis suggesting that the campaign has increased sales. Using sample data, you would apply the appropriate test (e.g., t-test) to determine whether the results support or reject the null hypothesis. This example teaches you how to structure and carry out hypothesis tests, an important skill for analytical assessments.
These practical examples are designed to reinforce key concepts and enhance your ability to solve problems effectively. The more you practice, the more confident you will feel in applying your knowledge during the test.
Strategies for Multiple Choice Questions
Multiple choice questions can be challenging, but with the right approach, you can maximize your chances of success. These questions often require not only knowledge but also strategy to navigate effectively. In this section, we will discuss key techniques to help you tackle these questions with confidence, reduce common mistakes, and improve your overall performance.
Understanding the Question and Options
Before making a selection, carefully read both the question and all available options. Sometimes, questions include keywords that guide you toward the correct answer. Pay attention to qualifiers like “always,” “never,” or “sometimes,” which can provide hints about the correct choice. Here are some tips:
- Eliminate obvious incorrect answers: Start by crossing out any choices that are clearly wrong.
- Look for keywords: Focus on words that might help you narrow down the correct answer, such as “most likely” or “least likely.”
- Use logic: If two answers are similar, one is usually more specific or correct. Choose the more precise option.
Use Process of Elimination
If you’re unsure about the correct answer, use the process of elimination to narrow down your choices. Removing one or two obviously incorrect answers increases your chances of selecting the right one. Here’s how you can apply this strategy:
| Step | Description |
|---|---|
| Step 1 | Read the question and all options carefully. |
| Step 2 | Eliminate any answers that are obviously wrong. |
| Step 3 | Consider the remaining options carefully, choosing the one that makes the most sense based on your knowledge. |
| Step 4 | If still unsure, make an educated guess by selecting the best remaining option. |
By focusing on the structure of the question and applying these strategies, you can increase your accuracy and efficiency in answering multiple choice questions.
Study Resources for Better Understanding
Having access to the right study materials can make all the difference when preparing for a challenging test. A variety of resources are available that can enhance your understanding of key concepts and improve retention. This section will guide you through different tools and methods that can provide deeper insights, helping you build confidence and competence in your studies.
Books and Textbooks
Textbooks are an essential resource, offering comprehensive coverage of the topics you need to learn. They often break down concepts step by step, with examples and exercises that reinforce key ideas. Be sure to read the chapters thoroughly and review any practice problems to solidify your understanding. Consider these strategies when using textbooks:
- Focus on Summary Sections: Most textbooks provide summaries at the end of each chapter that highlight the key points. Review these summaries to reinforce important concepts.
- Work Through Examples: Apply what you’ve learned by solving example problems. This practice will deepen your understanding and prepare you for real questions.
- Highlight Key Definitions: Mark definitions and formulas to quickly reference when needed.
Online Learning Platforms
Online platforms provide an interactive and flexible way to study, offering video tutorials, quizzes, and community forums. These platforms allow you to learn at your own pace and focus on areas where you need the most improvement. Consider using these online resources:
- Khan Academy: Offers free video lessons on a variety of topics, providing in-depth explanations and practice exercises.
- Coursera: Features courses from universities and institutions, often with peer reviews and quizzes to assess your progress.
- Quizlet: Create your own flashcards or use pre-made sets to test your knowledge on key terms and concepts.
By combining textbooks with online resources, you can take a well-rounded approach to studying, ensuring that you cover all the necessary material from multiple perspectives.
Reviewing Key Statistical Distributions
Understanding the various types of distributions is crucial for interpreting data and drawing conclusions from it. These distributions represent how values in a dataset are spread out, and each one has distinct properties that can help solve different types of problems. In this section, we’ll review some of the most common distributions that are often encountered in data analysis, focusing on their characteristics and when they should be applied.
Normal Distribution
The normal distribution is one of the most widely known and used in data analysis. It is symmetrical and bell-shaped, where most of the data points are clustered around the mean. Understanding the properties of the normal distribution is essential for making inferences about populations based on sample data. Key aspects of this distribution include:
- Symmetry: The distribution is symmetric around the mean, meaning the left and right sides are mirror images of each other.
- Empirical Rule: About 68% of data points fall within one standard deviation from the mean, 95% within two, and 99.7% within three.
- Application: This distribution is often used in hypothesis testing, confidence intervals, and many real-world scenarios where data tends to cluster around a central value.
Binomial Distribution
The binomial distribution is used for scenarios where there are two possible outcomes, such as success or failure. This distribution is essential for understanding discrete events that occur a fixed number of times, such as coin flips or surveys. Key characteristics include:
- Two Outcomes: Each trial results in one of two outcomes: success or failure.
- Fixed Number of Trials: The number of trials is predetermined and constant throughout the experiment.
- Application: It is commonly applied in situations such as quality control, marketing surveys, and clinical trials.
By understanding these distributions, you will be better equipped to analyze data accurately and make informed decisions based on the type of data you encounter.
Analyzing Trends with Regression Models
Regression models are powerful tools used to understand relationships between variables and predict future outcomes. By fitting a model to data, you can identify trends, assess the strength of relationships, and make informed predictions. In this section, we will explore the fundamentals of regression analysis, focusing on its application in trend analysis and forecasting.
Simple Linear Regression
Simple linear regression is the most basic form of regression analysis, where the relationship between two variables is modeled as a straight line. This model is used when one variable is dependent on another, and it helps to predict the dependent variable based on the independent variable. Key components of simple linear regression include:
- Line of Best Fit: The model attempts to draw the line that best represents the relationship between the two variables, minimizing the distance between the data points and the line.
- Equation: The relationship is expressed through the equation y = mx + b, where y is the dependent variable, x is the independent variable, m is the slope, and b is the y-intercept.
- Prediction: Once the model is established, it can be used to predict the value of y for any given x value.
Multiple Linear Regression
In many real-world situations, the relationship between variables is more complex and involves more than one independent variable. Multiple linear regression extends the simple linear regression model to accommodate multiple predictors. It allows you to model the relationship between one dependent variable and several independent variables. Key features include:
- Multiple Predictors: Multiple independent variables are used to predict the dependent variable.
- Equation: The model is represented by the equation y = b₀ + b₁x₁ + b₂x₂ + … + bₖxₖ, where each b value represents the coefficient of the corresponding independent variable.
- Interpretation: The coefficients show the impact of each predictor on the dependent variable, allowing you to assess the strength and direction of each relationship.
By analyzing trends with regression models, you can gain valuable insights into patterns and use these findings for forecasting and decision-making in various fields, from finance to healthcare and beyond.
Dealing with Complex Word Problems
Word problems can often appear daunting, especially when they involve multiple steps or concepts. However, breaking down the problem into manageable parts and following a logical process can help simplify even the most complicated scenarios. In this section, we’ll explore effective strategies for approaching and solving complex word problems with confidence.
Step-by-Step Approach
When faced with a complex word problem, it’s essential to follow a structured approach to ensure accuracy and efficiency. Here’s a general process that you can use:
- Read Carefully: Start by reading the problem carefully, noting important details such as numbers, units, and relationships between variables.
- Identify the Question: Focus on what is being asked. This will help you determine which information is relevant and what you need to find.
- Extract Key Information: Highlight or underline key data points and relationships between variables that will help you solve the problem.
- Translate into Mathematical Form: Convert the problem into a mathematical expression or equation that you can work with. This may involve defining variables or creating formulas based on the given data.
- Solve Step-by-Step: Solve the problem one step at a time. If necessary, break it down into smaller sub-problems to avoid becoming overwhelmed.
- Check Your Work: After obtaining a solution, review your steps to ensure accuracy. Check that your answer makes sense in the context of the problem.
Example Problem

Let’s take a look at a sample problem to demonstrate this process:
| Step | Action |
|---|---|
| Step 1 | Read the problem carefully and highlight key information. |
| Step 2 | Identify what is being asked. Determine which variables you need to solve for. |
| Step 3 | Translate the problem into a mathematical equation, using the key data points. |
| Step 4 | Solve the equation using appropriate methods (e.g., substitution, elimination, etc.). |
| Step 5 | Check the solution and ensure it aligns with the context of the problem. |
By following these steps, you can simplify complex word problems and confidently find the correct solutions. Remember, practice is key, so don’t hesitate to work through similar problems to enhance your problem-solving skills.
Using Excel for Statistical Calculations
Microsoft Excel is a powerful tool for performing a wide range of numerical and analytical tasks. Whether you’re analyzing data trends, performing complex calculations, or generating graphs, Excel provides a suite of built-in functions and features to streamline the process. In this section, we’ll explore how to leverage Excel’s capabilities to make statistical tasks simpler and more efficient.
Key Functions for Data Analysis
Excel includes several functions specifically designed to aid in numerical analysis. Below are some of the most commonly used functions:
- AVERAGE: Calculates the mean of a data set. Simply use =AVERAGE(range) to find the average value of selected cells.
- MEDIAN: Returns the middle value in a data set when sorted. Use =MEDIAN(range) to apply this function.
- STDEV: Measures the standard deviation of a data set, helping you understand the spread of values. Use =STDEV(range) to calculate this.
- CORREL: Finds the correlation coefficient between two data sets, indicating how strongly they are related. Use =CORREL(range1, range2) for this calculation.
- VAR: Calculates variance, which is another measure of data spread. Use =VAR(range) to get the variance of your data.
Creating Visual Representations

Excel also allows you to visualize your data with charts and graphs, which can be essential for interpreting and presenting results. Here are a few common graph types:
- Bar Charts: Ideal for comparing data across categories. These are useful for visualizing differences in data points.
- Line Graphs: Great for showing trends over time or across different intervals.
- Scatter Plots: Excellent for identifying relationships or patterns between two variables.
- Histograms: Used to display the distribution of a data set by grouping values into ranges.
By utilizing Excel’s built-in functions and charting tools, you can efficiently analyze and interpret data for various tasks, saving time and increasing accuracy. Excel not only simplifies calculations but also enables you to communicate your findings in a clear and professional manner.
How to Stay Calm During the Test
Feeling nervous or stressed before and during a challenging assessment is a common experience. However, it is important to maintain composure in order to think clearly and make the best use of your knowledge. By adopting specific strategies, you can remain focused and reduce anxiety, allowing you to perform at your highest potential.
Preparation Techniques for Staying Calm
Proper preparation is one of the key factors in reducing test-related stress. Here are some tips that can help:
- Practice regularly: Consistent study habits lead to confidence. The more familiar you are with the material, the less likely you will be to panic.
- Simulate the test environment: Practice under timed conditions to get used to the pressure. This helps you manage time and stay calm during the actual assessment.
- Get enough rest: A well-rested mind performs better. Ensure you have a good night’s sleep before the test to stay sharp and focused.
- Stay hydrated and eat well: Proper nutrition and hydration can boost cognitive function and help you maintain energy levels.
Strategies for Staying Calm During the Test
During the test, it’s important to use effective strategies to maintain composure. Consider these techniques:
- Take deep breaths: Slow, deep breathing can help reduce physical symptoms of anxiety and allow you to focus.
- Read instructions carefully: Take your time to read through each question and understand what is being asked. This will prevent mistakes made under pressure.
- Start with easier questions: Begin with questions that you know well to build momentum and confidence. This can help alleviate stress for the more difficult ones later.
- Stay positive: Avoid negative thinking. If you encounter a tough question, take a deep breath and move on to others. You can always return to it later.
By incorporating these strategies into your test preparation and approach, you can manage stress more effectively, allowing you to stay calm and perform better under pressure.