
Geometry involves solving various problems that require a clear understanding of shapes, their properties, and relationships. One of the fundamental tasks is mastering how to work with quadrilaterals that have unique characteristics, such as opposite sides being equal and parallel. These figures are commonly found in both theoretical and practical applications, making it essential to grasp the methods used to calculate their areas, perimeters, and angles.
In this guide, we will explore the steps needed to solve these types of geometric challenges effectively. By breaking down each problem into manageable parts, you’ll gain the skills necessary to approach these figures confidently. Whether you’re learning for the first time or refining your knowledge, the key lies in understanding the core principles and applying them systematically.
Clear and precise calculations are essential for mastering these topics. Using the correct formulas and strategies will allow you to tackle even the most complex scenarios with ease. Through practice and familiarization with these concepts, solving related problems will become a straightforward task, ensuring both accuracy and efficiency.
Geometric Problem Solutions Overview

This section focuses on providing a comprehensive look at solving geometric challenges related to quadrilaterals with parallel sides. Understanding how to approach these problems systematically is essential for successfully calculating key properties such as area, perimeter, and angles. By breaking down the problem-solving process into clear steps, learners can gain confidence in their ability to tackle similar tasks in the future.
Each problem typically involves identifying specific characteristics of the shape, applying the appropriate formulas, and interpreting the results in a logical manner. By practicing with a variety of examples, you’ll be able to refine your skills and better understand the underlying mathematical principles.
| Topic | Key Concept | Common Formula |
|---|---|---|
| Area Calculation | Length of base and height | Area = Base × Height |
| Perimeter Calculation | Sum of all sides | Perimeter = 2 × (Base + Side) |
| Angle Relationships | Opposite angles are equal | Angle A = Angle C, Angle B = Angle D |
By understanding these concepts and applying them correctly, you can solve problems efficiently and accurately. Practicing these types of problems will help solidify your knowledge and ensure you are well-prepared for more advanced topics in geometry.
Understanding Parallelogram Properties
To solve geometric problems involving shapes with opposite sides that are both equal and parallel, it is essential to understand their unique properties. These figures exhibit several defining characteristics that distinguish them from other quadrilaterals, and mastering these properties is key to solving related problems. Let’s explore the most important features of these shapes.
- Opposite sides are equal: Each pair of opposite sides has the same length.
- Opposite angles are equal: The angles on opposite corners are congruent.
- Diagonals bisect each other: The diagonals divide each other into two equal parts at the point of intersection.
- Consecutive angles are supplementary: Adjacent angles add up to 180 degrees.
- Parallel sides: The opposite sides are parallel to each other, ensuring equal spacing throughout the shape.
These fundamental properties provide a strong foundation for solving various problems related to such shapes. Whether calculating area, perimeter, or angle measures, understanding these key traits allows for more accurate problem-solving. Additionally, recognizing these characteristics helps in identifying the shape in real-world contexts.
- Identify opposite sides and angles.
- Use formulas based on the properties to calculate dimensions.
- Apply these properties to solve for unknown values in geometric tasks.
By familiarizing yourself with these core aspects, you’ll be better equipped to approach and solve a variety of geometric challenges involving these specific types of figures.
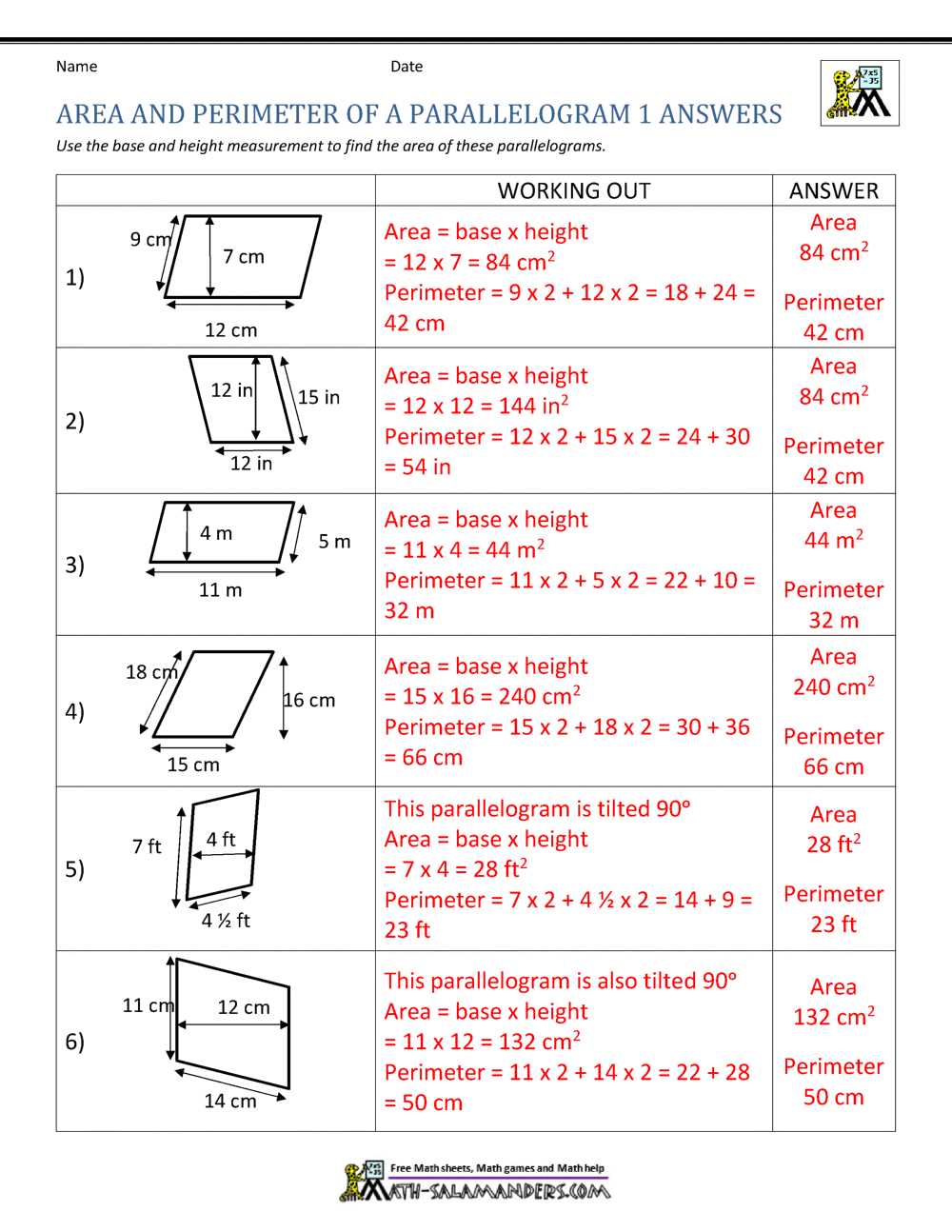
How to Calculate Parallelogram Area
Calculating the area of a quadrilateral with opposite sides that are both equal and parallel is a straightforward process once you know the correct formula. The area of such a figure depends on the length of the base and the corresponding height. Understanding how these two measurements relate to the total space enclosed by the shape is key to performing the calculation correctly.
To calculate the area, you need to follow these steps:
- Identify the base of the figure: This is one of the sides that is parallel to the opposite side.
- Measure the height: This is the perpendicular distance between the base and the opposite side.
- Use the formula: Area = Base × Height
Make sure to use consistent units of measurement for both the base and the height. The resulting area will be in square units, corresponding to the units you used for the base and height.
- Example 1: If the base is 10 cm and the height is 5 cm, the area will be 50 cm².
- Example 2: For a base of 8 meters and a height of 3 meters, the area is 24 m².
By applying this simple formula, you can easily find the area of any shape with these properties, whether for academic problems or real-world applications.
Finding Perimeter of Parallelograms
To determine the perimeter of a quadrilateral with opposite sides that are both equal and parallel, you simply need to add up the lengths of all four sides. The perimeter represents the total distance around the figure, and for shapes with these specific properties, the formula is quite straightforward. This calculation requires knowing the lengths of just two sides: the base and the side that connects the parallel sides.
Steps to Calculate Perimeter

- Measure the base length: This is the length of one of the parallel sides.
- Measure the side length: This is the distance between the two parallel sides.
- Apply the formula: Perimeter = 2 × (Base + Side)
For accuracy, ensure that both the base and the side are measured in the same units. Once the values are added together, multiply the result by 2 to account for both pairs of equal sides.
Example Calculations
- Example 1: For a base of 6 cm and a side of 4 cm, the perimeter is 2 × (6 + 4) = 20 cm.
- Example 2: If the base is 10 meters and the side is 5 meters, the perimeter is 2 × (10 + 5) = 30 meters.
Using this method, you can easily determine the perimeter of any shape with parallel and equal sides. It’s a useful tool for solving geometric problems in both academic settings and real-life applications.
Step-by-Step Guide to Solving Problems
When tackling geometric challenges involving quadrilaterals with equal and parallel opposite sides, following a structured approach can simplify the process. By breaking down the problem into smaller, manageable steps, you can ensure accuracy and build confidence in your problem-solving abilities. Whether you’re calculating the area, perimeter, or other properties, a methodical approach will help you arrive at the correct solution.
Steps to Solve Geometric Problems
- Read the problem carefully: Identify what information is given and what needs to be determined. Make note of the dimensions and relationships between the sides and angles.
- Choose the correct formula: Based on the properties of the shape, select the formula needed for your calculations, such as those for area, perimeter, or angles.
- Plug in the values: Substitute the known measurements into the formula. Ensure that all units are consistent to avoid errors.
- Perform the calculations: Follow the order of operations to solve the equation. Double-check your work for any possible mistakes.
- Verify your result: Review the answer to ensure it makes sense in the context of the problem. If the problem involves real-world scenarios, check that your result is practical.
Example Problem Solving
- Example 1: If the base is 10 cm and the height is 5 cm, use the formula for area: Area = Base × Height, which gives 10 × 5 = 50 cm².
- Example 2: For a shape with a base of 8 meters and a side of 6 meters, use the formula for perimeter: Perimeter = 2 × (Base + Side), which gives 2 × (8 + 6) = 28 meters.
By following this structured approach, you can easily navigate through problems and confidently find the solution. Practice with different scenarios to improve your ability to solve geometric problems effectively.
Common Mistakes in Parallelogram Worksheets
When solving geometric problems involving quadrilaterals with parallel and equal opposite sides, there are several common errors that can lead to incorrect results. These mistakes often occur when the properties of the shape are misunderstood or when the wrong approach is applied. Recognizing these pitfalls is essential to improving accuracy and avoiding frustration.
| Mistake | Explanation | How to Avoid |
|---|---|---|
| Incorrect measurement of height | Confusing the height with a side length, leading to inaccurate area calculations. | Ensure the height is the perpendicular distance between the parallel sides, not the length of the slanted side. |
| Forgetting to use the correct formula | Using a formula meant for different shapes, such as rectangles, instead of one specific to the given shape. | Double-check the formula based on the properties of the figure you are working with. |
| Mixing up units | Using inconsistent units for measurements, leading to incorrect results. | Always ensure that all measurements are in the same unit (e.g., all in centimeters or meters). |
| Misunderstanding angle properties | Assuming all angles are 90 degrees, which is not true for all quadrilaterals with parallel sides. | Remember that only the opposite angles are equal, and they may not necessarily be 90 degrees. |
By being aware of these common mistakes and actively avoiding them, you can ensure that your geometric calculations are more accurate and reliable. Careful attention to detail and a solid understanding of the properties of the shape are key to overcoming these challenges.
Key Formulas for Parallelogram Problems
When solving geometric problems involving quadrilaterals with opposite sides that are both parallel and equal, there are several important formulas you need to know. These formulas allow you to find essential measurements such as area, perimeter, and other properties of the shape. Mastering these formulas is crucial for accurate problem-solving and calculation.
Area Formula
The area of a quadrilateral with parallel sides can be calculated by multiplying the length of the base by the perpendicular height. This formula is simple yet essential:
Area = Base × Height
Here, the base refers to the length of one of the parallel sides, and the height is the perpendicular distance between the parallel sides. Make sure that both measurements are in the same unit for consistency.
Perimeter Formula
The perimeter of this type of quadrilateral is found by adding up the lengths of all four sides. Since opposite sides are equal in length, you only need to know the lengths of two sides:
Perimeter = 2 × (Base + Side)
In this formula, the Base refers to one of the parallel sides, and the Side refers to the length of the non-parallel side. Once you have these values, simply multiply their sum by 2.
These two formulas will help you tackle most basic problems involving shapes with equal and parallel opposite sides. Understanding how to apply them correctly is essential for finding accurate solutions in geometry.
Using Diagonals to Solve Parallelograms
Diagonals can be powerful tools when working with quadrilaterals that have equal and parallel opposite sides. These line segments, which connect opposite corners of the shape, can reveal useful properties and provide a different perspective for solving various geometric problems. By understanding how to use diagonals effectively, you can simplify complex calculations and uncover relationships that might not be immediately obvious.
One key property of diagonals in these shapes is that they bisect each other, meaning they divide each other into two equal parts. This fact can help in determining unknown side lengths, angles, and areas when combined with other geometric principles. Additionally, diagonals can sometimes be used to break the shape into two triangles, allowing you to apply triangle-related formulas for easier calculation.
To solve problems involving diagonals, it’s important to know the following:
- Diagonal Length Formula: In certain cases, the lengths of the diagonals can be found using the Pythagorean theorem if enough other measurements are known.
- Angle Relationships: The angles formed by the intersection of the diagonals can provide valuable information, especially when solving for unknown angles or sides.
Incorporating diagonals into your geometric problem-solving toolkit allows for a deeper understanding of the shape and can make seemingly difficult problems much more manageable.
How Angles Relate to Parallelograms
Angles play a crucial role in understanding the properties of quadrilaterals with opposite sides that are both parallel and equal. These geometric figures have unique angle relationships that can simplify problem-solving and help you determine unknown values. By understanding how angles interact within these shapes, you can use these properties to solve for missing measurements or verify your calculations.
In such shapes, opposite angles are always equal. This means that if you know the measure of one angle, you can immediately determine the measure of the angle directly across from it. Additionally, consecutive angles–those next to each other–are supplementary, meaning they always add up to 180 degrees. This property can be extremely helpful when solving for unknown angles within the shape.
For example, if you are given one angle and need to find another, knowing these relationships allows you to use simple subtraction or addition to quickly arrive at the correct answer. These angle properties form the foundation for solving many geometric problems involving these shapes.
Real-World Applications of Parallelograms
Geometric shapes with opposite sides that are both parallel and equal in length have numerous practical uses in the real world. These shapes appear frequently in everyday objects, structures, and designs. Understanding how these figures function in the real world can provide valuable insights into both mathematics and applied fields such as architecture, engineering, and art.
Engineering and Architecture
In engineering and construction, shapes with parallel sides are often used in structural designs, such as bridges, roofs, and trusses. The ability to distribute weight evenly across parallel sides enhances the stability of these structures. These geometric principles are used to calculate load-bearing capacities and ensure that buildings and bridges remain safe and secure under various conditions.
Graphic Design and Art

In graphic design, these shapes are commonly found in logos, patterns, and artwork. The balanced, symmetrical nature of shapes with parallel sides makes them visually appealing and useful for creating harmonious designs. In art, such shapes are often used to create perspective, where parallel lines help guide the viewer’s eye toward a vanishing point or focal area.
From structural applications to artistic designs, shapes with parallel sides are essential in both functional and aesthetic contexts, demonstrating the versatility and importance of geometry in various fields.
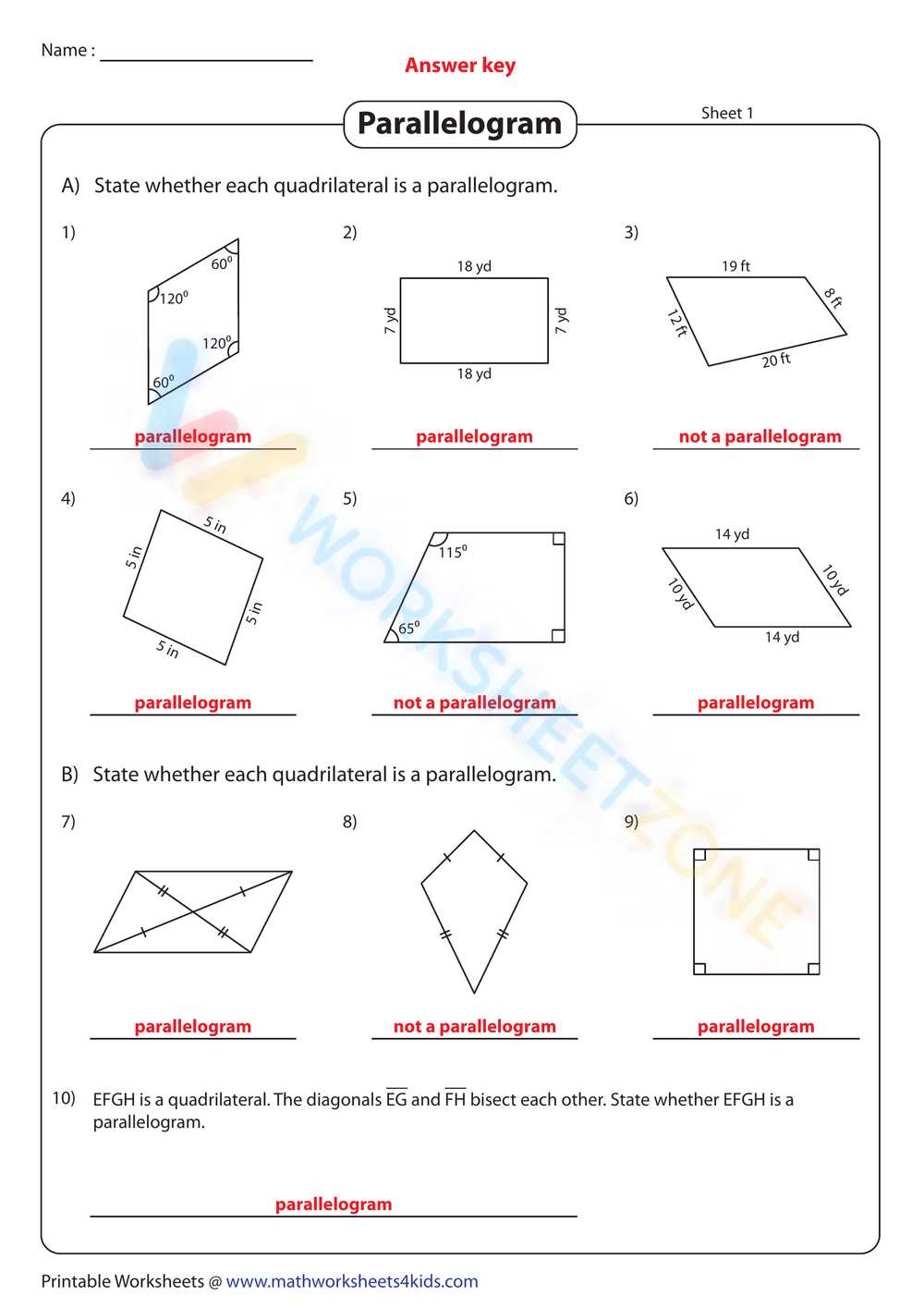
Types of Parallelograms Explained
There are several specific types of quadrilaterals with opposite sides that are both parallel and equal in length, each with its own unique properties and characteristics. Understanding the distinctions between these types can help you solve problems more effectively and apply geometric principles in various situations. Below are some of the most common types of these shapes, each with their own defining features.
- Rectangle: A quadrilateral with four right angles. The opposite sides are equal and parallel, and the diagonals are of equal length.
- Rhombus: A quadrilateral where all four sides are of equal length. The opposite angles are equal, and the diagonals bisect each other at right angles.
- Square: A special type of rectangle and rhombus where all sides are equal in length and all angles are 90 degrees. The diagonals are equal in length and bisect each other at right angles.
- Rhomboid: A quadrilateral where opposite sides are equal and parallel, but the angles are not necessarily 90 degrees. The diagonals bisect each other but are not of equal length.
Each type of shape has its own set of geometric properties that can be used in different contexts, from architecture to design to mathematical problem-solving. By understanding these differences, you can apply the right methods and formulas for each specific case.
Visualizing Parallelograms in Geometry
In geometry, the ability to visualize certain shapes can make it much easier to understand their properties and solve related problems. Quadrilaterals with opposite sides that are both parallel and equal in length have distinct characteristics that can be better understood through visual representation. By drawing these figures, you can gain insights into their symmetry, angles, and relationships between sides, making calculations more intuitive.
When visualizing such shapes, it’s important to focus on the key features that define them, such as parallelism, angle relationships, and symmetry. Drawing these shapes to scale helps to better understand how the sides and angles interact with one another, which is crucial for solving geometric problems accurately.
| Shape | Key Features | Visual Clue |
|---|---|---|
| Rectangle | Four right angles, opposite sides equal and parallel | All angles are 90 degrees, opposite sides are equal |
| Rhombus | All sides equal, opposite angles equal, diagonals bisect each other | Diagonal intersection at right angles, equal side lengths |
| Square | All sides equal, four right angles | Perfect symmetry, equal sides, right angles |
| Rhomboid | Opposite sides parallel, opposite angles equal, diagonals bisect each other | Slanted sides, non-right angles, unequal diagonals |
By creating accurate drawings of these shapes, you can better understand their properties and use this knowledge to solve problems related to areas, perimeters, angles, and other geometric aspects. This visualization also aids in recognizing the relationships between different types of quadrilaterals, helping to build a deeper understanding of geometry as a whole.
Tips for Solving Parallelogram Problems Fast
Solving geometry problems related to quadrilaterals with parallel opposite sides can often seem challenging, but with the right strategies, you can approach these problems more efficiently. By following some helpful tips, you can reduce the time it takes to find solutions and avoid common mistakes. The key is to develop a methodical approach that allows you to quickly identify the important information and apply the appropriate formulas or techniques.
- Understand the Basic Properties: Always recall that opposite sides are equal in length and parallel. This foundational knowledge will help you quickly recognize the key aspects of the problem.
- Use Diagonals to Simplify: Often, breaking the shape into triangles using diagonals can make it easier to solve for unknown areas or side lengths.
- Memorize Key Formulas: Knowing the formulas for calculating area and perimeter will save valuable time. For example, the area of a shape is typically the base times the height, while the perimeter is the sum of all four sides.
- Draw Accurate Diagrams: A clear sketch of the shape can help you visualize angles, lengths, and relationships, which will make calculations more straightforward.
- Look for Symmetry: Symmetry often simplifies problems. If the shape has any symmetrical properties, use them to make deductions more quickly.
- Practice with Different Problem Types: The more problems you solve, the faster you will recognize patterns and apply the correct methods instinctively.
By implementing these strategies and staying focused on the core properties of the shape, you can quickly solve problems involving geometric figures with parallel sides. Practice and familiarity with the formulas and techniques will help you become more confident and efficient over time.
Advanced Techniques for Parallelogram Analysis
When working with quadrilaterals that have opposite sides that are both equal and parallel, employing advanced strategies can greatly enhance your ability to solve complex problems efficiently. These techniques go beyond basic calculations and help in deeper understanding and problem-solving. They often involve leveraging geometric properties, algebraic methods, and computational tools that allow for quicker analysis and more accurate results.
One of the most powerful approaches is using coordinate geometry. By placing the shape on a coordinate plane, you can use the distance formula to calculate side lengths, and the slope formula to verify parallelism between opposite sides. This method is particularly useful when dealing with irregularly shaped figures or when precise measurements are required.
Another advanced technique is the use of vectors to describe the sides and diagonals of the shape. By representing the sides as vectors, you can apply vector addition and subtraction to determine unknown quantities, such as angles or lengths, without relying on traditional geometry formulas. This method is useful in more complex problems where multiple steps and calculations are needed.
Additionally, working with transformations such as rotations, reflections, and translations can simplify analysis. These techniques allow you to manipulate the shape in various ways that preserve key properties, enabling you to identify patterns or symmetries that would not be immediately obvious. By recognizing these transformations, you can apply them to reduce the problem to a simpler one.
Finally, computer software and graphing calculators can assist in solving particularly challenging problems. Tools like geometric visualization programs or algebraic solvers can help automate tedious calculations, allowing you to focus on the conceptual understanding of the problem. While these tools are not a substitute for mathematical knowledge, they can significantly speed up the process when used properly.
Incorporating these advanced techniques into your problem-solving toolkit will not only help you tackle more challenging problems but also deepen your understanding of geometric shapes and their properties.
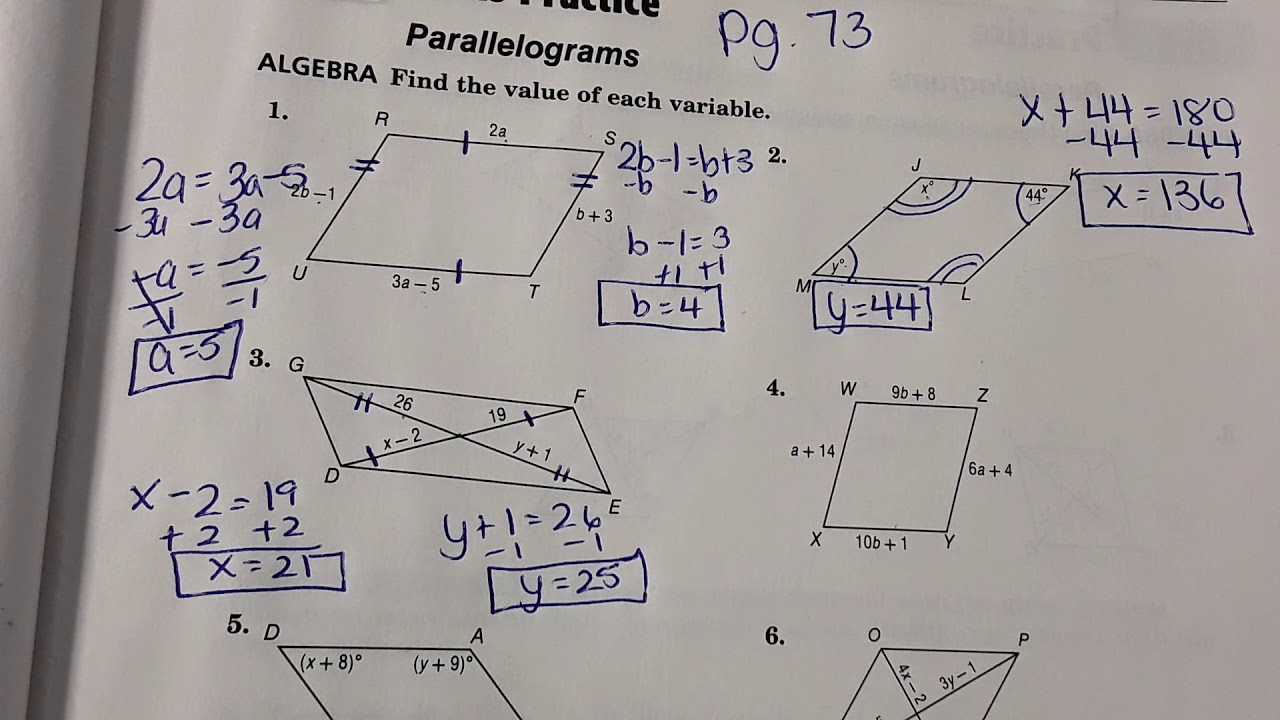
Common Parallelogram Theorems to Know
Understanding the fundamental theorems related to quadrilaterals with opposite sides equal and parallel is essential for solving problems efficiently. These theorems provide important properties that can simplify complex tasks and guide you toward accurate solutions. By mastering these key concepts, you’ll be able to quickly recognize patterns, calculate areas, and apply various formulas with ease.
Opposite Sides Are Equal
One of the most well-known properties of these quadrilaterals is that the opposite sides are always equal in length. This theorem states that if a shape has two pairs of opposite sides that are parallel, then those sides must also be congruent. This property is foundational when calculating perimeter and is often used as a shortcut to verify the shape’s consistency.
Opposite Angles Are Congruent
Another important theorem is that opposite angles in such quadrilaterals are always congruent. This means that the angles located opposite one another in the shape will always have the same measure. This rule is crucial when working with angle relationships, such as when solving for missing angle values or proving that a quadrilateral is a specific type of geometric figure.
Diagonals Bisect Each Other
A lesser-known but equally useful theorem is that the diagonals of these shapes bisect each other. In simpler terms, the diagonals cut each other into two equal parts. This property is particularly helpful in coordinate geometry when working with equations of lines and finding intersection points of the diagonals.
These theorems form the basis for most calculations and proofs involving this type of shape. Whether you’re dealing with basic calculations or tackling more complex geometric problems, keeping these key theorems in mind will allow you to approach each task with confidence.
Interactive Tools for Parallelogram Learning

Engaging with interactive tools can significantly enhance the learning experience when studying shapes with opposite sides parallel and equal. These resources provide dynamic ways to visualize and explore geometric properties, making complex concepts easier to understand. By using these tools, learners can experiment with different configurations, test their knowledge, and reinforce key concepts in a fun and intuitive way.
Geometry Simulators and Visualizers
Geometry simulators allow users to manipulate the dimensions of shapes, adjusting angles, sides, and diagonals in real-time. These tools offer a hands-on approach to learning by visually demonstrating how changes in one part of the shape affect the rest. They help learners build a deeper understanding of geometric relationships and improve spatial reasoning skills.
Online Quizzes and Problem Solvers
Online quizzes are an excellent way to test one’s knowledge and reinforce learning. These platforms often offer immediate feedback, allowing users to see where they made mistakes and how to correct them. Problem solvers, on the other hand, guide learners step-by-step through solving geometric problems, ensuring that key concepts are applied correctly and consistently.
Incorporating these interactive tools into the learning process not only enhances comprehension but also keeps the material engaging. With immediate feedback and hands-on experimentation, learners can strengthen their understanding and build confidence in their geometric abilities.
Improving Speed with Parallelogram Exercises
Practicing geometric exercises can significantly improve both your speed and accuracy in solving problems related to shapes with parallel sides. The more you engage with these exercises, the quicker you’ll recognize patterns, understand properties, and apply formulas effectively. Consistent practice helps to streamline your problem-solving process and boosts confidence in working with these shapes.
Strategies to Improve Efficiency
To increase your speed, it’s important to focus on the following strategies:
- Master Basic Formulas: Memorizing key formulas for area, perimeter, and angles is the first step to speeding up problem-solving.
- Recognize Symmetry: Identifying symmetrical properties in the shape allows for quicker solutions without overthinking each step.
- Practice Mental Math: Enhancing mental math skills allows for faster calculations without needing to rely on a calculator or written work.
- Work on Visualization: Being able to visualize the shape in your mind helps reduce time spent on drawing and setup during problem-solving.
Tracking Progress and Reducing Time
Tracking your progress over time is a key way to measure improvements. As you practice, you’ll start to see patterns in how you approach different types of problems. Over time, these patterns will help you solve problems more quickly and efficiently. To assist in this process, many online tools provide timed challenges, which encourage you to solve problems faster while maintaining accuracy.
Consistent practice with these techniques and exercises will lead to significant improvements in speed, allowing you to solve geometric problems in less time and with greater ease.