
Mathematics can be a challenging subject, especially when faced with an important assessment that covers a wide range of topics. Mastering the material requires not just practice but also a solid understanding of key concepts that will be tested. Whether you’re reviewing complex functions or problem-solving strategies, effective preparation is crucial to achieving success.
Effective study methods involve not only working through sample questions but also familiarizing yourself with the types of problems that will appear. It is essential to develop a structured approach to reviewing each topic systematically. This will help reinforce your understanding and ensure you’re well-prepared to tackle the test with confidence.
Success lies in practice and persistence. By focusing on your weak areas and reinforcing your strengths, you can approach the test with clarity and control. Being prepared isn’t just about memorizing formulas; it’s about applying your knowledge accurately and efficiently under time pressure.
Apex Algebra 2 Semester 1 Exam Answers
In order to succeed in a challenging mathematics test, it’s essential to have a clear understanding of both the core concepts and the types of problems you’re likely to encounter. Effective preparation goes beyond simple memorization; it involves applying learned principles to solve complex questions under pressure. By mastering the material from the first portion of the course, you can approach the test with confidence and accuracy.
To perform well on assessments of this nature, reviewing key areas such as functions, equations, and advanced problem-solving techniques is crucial. It’s not only about knowing the formulas but also understanding how to use them in context. Practice with a variety of question types will also help develop the skills needed to approach unfamiliar problems with ease.
Taking time to work through sample problems and reviewing past materials will help reinforce your understanding and improve problem-solving speed. This process of repetition and self-testing is essential for success, as it prepares you for the format and pace of the actual test. With focused preparation, you can increase your chances of achieving a high score.
Understanding the Algebra 2 Curriculum
To perform well in a mathematics course focused on advanced functions and equations, it’s important to have a deep understanding of the key topics covered throughout the term. The curriculum typically spans a variety of mathematical concepts, from the foundations of quadratic relationships to more complex functions involving exponents and logarithms. Gaining a solid grasp of these ideas will enable you to solve problems with ease and efficiency.
Throughout the course, students are introduced to both theoretical principles and practical problem-solving methods. Key areas often include systems of equations, polynomial functions, and rational expressions. Understanding these core topics not only prepares you for the test but also helps you to apply the concepts to real-world scenarios, making them more accessible and meaningful.
Each section builds on previous knowledge, so it’s essential to review foundational concepts regularly. By revisiting earlier lessons, you can strengthen your understanding and make connections between different topics, which will improve your overall performance and problem-solving abilities.
Key Topics Covered in Semester 1
The first part of a mathematics course focused on advanced functions introduces a variety of foundational concepts that are essential for understanding more complex topics. These core areas provide the building blocks for solving problems and mastering more advanced techniques. Familiarity with these subjects is crucial for both practical application and academic success.
Core Concepts and Functions
Several key areas are explored, each of which plays a significant role in the overall curriculum. These topics provide the tools needed to approach problems logically and systematically.
- Linear Equations and Inequalities
- Systems of Linear Equations
- Quadratic Functions and Their Properties
- Exponential Functions
- Polynomials and Rational Expressions
Problem Solving and Applications
In addition to learning the theory behind each topic, students focus on applying these principles in real-world situations. Mastery of these topics will not only improve test performance but will also sharpen critical thinking and analytical skills.
- Graphing and Interpreting Functions
- Solving Complex Word Problems
- Using Mathematical Models in Real-Life Scenarios
- Working with Rational Functions and Asymptotes
How to Approach Test Questions
When faced with a challenging assessment, having a structured approach can make all the difference in how effectively you perform. By staying organized and focused, you can tackle even the most difficult problems with confidence. Understanding the format of the questions and practicing problem-solving techniques will help you answer efficiently and accurately.
Start by reading each question carefully to ensure you understand what is being asked. Often, questions may contain subtle hints or extra information that can guide you toward the right solution. Take your time and highlight important details, such as key values or specific instructions.
Break down complex problems into smaller steps. This will help simplify the process and prevent you from feeling overwhelmed. If you encounter a particularly difficult question, move on to the next one and come back to it later with a fresh perspective. Consistent practice of these strategies will improve your ability to approach problems logically and without haste.
Common Challenges in Algebra 2 Exams
Mathematics assessments often present a variety of obstacles that test both conceptual understanding and problem-solving ability. Students frequently encounter difficulties with certain topics that require a higher level of critical thinking and application. Recognizing these common challenges can help you focus your preparation efforts and build confidence for the test.
One of the most common difficulties is dealing with complex equations, where multiple steps are required to simplify or solve. Problems involving polynomials, rational expressions, and quadratic functions can be tricky, as they often require careful manipulation of variables and constants. Mistakes in these areas typically arise from misunderstanding how to approach each step of the problem or overlooking key components in the equation.
Another frequent challenge is interpreting word problems, which often involve translating real-world scenarios into mathematical expressions. These problems require both a solid grasp of the relevant concepts and the ability to identify and apply the correct methods. Without careful analysis, it’s easy to misinterpret the information and make errors in calculation or reasoning.
Helpful Study Tips for Algebra 2
Effective preparation for a mathematics test requires more than just reading through notes; it involves developing a strategy that includes active learning and consistent practice. By organizing your study sessions and focusing on key areas, you can build the skills necessary to perform well on challenging assessments. Implementing a few proven techniques can help improve both understanding and retention of the material.
Start by breaking down the material into smaller sections. Instead of trying to cover everything at once, focus on one topic at a time. Review key concepts, formulas, and methods that are most commonly tested, ensuring you fully understand how and when to apply them. This approach allows for more in-depth learning and reduces the feeling of being overwhelmed.
Practice regularly with sample problems to reinforce your understanding. Actively working through questions not only improves problem-solving speed but also helps you identify areas where you may need more practice. Be sure to review both correct and incorrect answers to understand any mistakes and avoid them in the future.
Finally, don’t hesitate to seek help when needed. Whether through online resources, study groups, or your teacher, asking for clarification on difficult topics can provide valuable insights and prevent confusion later on. Collaboration and discussion with others often lead to a deeper understanding of complex concepts.
Effective Time Management for Exams
Managing your time effectively during a test is essential to ensure that you complete all questions accurately and thoroughly. Proper time allocation helps you avoid rushing through problems, which can lead to unnecessary mistakes. By developing a strategy that balances speed and precision, you can maximize your performance and increase your confidence during the assessment.
Prioritizing and Planning
Before diving into the questions, take a moment to quickly scan the entire test. This will give you an idea of the length and difficulty of each section. By organizing your approach, you can allocate more time to challenging problems while ensuring that you have enough time for easier ones.
- Start with questions you feel most confident about to gain momentum.
- Allocate more time to complex questions or sections that require multiple steps.
- Keep an eye on the clock, but avoid checking it too frequently as it can cause stress.
Practicing Under Time Constraints
One of the best ways to improve your time management skills is through practice. Taking practice tests under timed conditions can help you get accustomed to the pressure and pace of the real assessment. By doing so, you can refine your strategy and become more comfortable with managing time during actual tests.
- Set time limits when completing practice questions or mock tests.
- Focus on finishing each section within the designated time frame.
- Review your mistakes afterward to improve both speed and accuracy.
Mastering Quadratic Equations and Functions
Quadratic equations and their corresponding functions form a crucial part of any advanced mathematics course. Understanding how to solve these equations and interpret their graphs is essential for progressing to more complex topics. By mastering these concepts, you can build a strong foundation for tackling a variety of problems that involve polynomial relationships.
Key Concepts in Quadratic Equations
At the heart of quadratic equations are their standard form and the methods used to solve them. Learning to identify and apply different solving techniques, such as factoring, completing the square, and using the quadratic formula, is fundamental to success in this area.
- Recognize the general form: ax² + bx + c = 0
- Factor the equation when possible, or use the quadratic formula to find the roots.
- Understand how to complete the square to convert the equation into vertex form.
Graphing Quadratic Functions
In addition to solving quadratic equations, it’s important to understand how to graph quadratic functions. These functions represent parabolic curves, and their graphs provide visual insight into the solutions and key properties, such as the vertex and axis of symmetry.
- Identify the vertex, axis of symmetry, and direction of the parabola (upward or downward).
- Understand the significance of the discriminant in determining the number of real solutions.
- Practice graphing by plotting key points, including the vertex and intercepts.
Trigonometry Fundamentals in Algebra 2
Trigonometry is an essential branch of mathematics that deals with the relationships between the sides and angles of triangles. In more advanced studies, understanding how to apply trigonometric functions and solve problems related to angles is key. This section explores the core concepts that will help you grasp the basics of trigonometry and apply them to various mathematical challenges.
At the heart of trigonometry lies the use of specific functions to relate angles to side lengths in right triangles. These functions–sine, cosine, and tangent–are the building blocks of trigonometric calculations. They are frequently used to solve problems that involve angles and distances, making them highly applicable in both geometry and calculus.
| Function | Formula | Description |
|---|---|---|
| Sine (sin) | sin(θ) = opposite/hypotenuse | Relates the angle to the ratio of the opposite side to the hypotenuse in a right triangle. |
| Cosine (cos) | cos(θ) = adjacent/hypotenuse | Relates the angle to the ratio of the adjacent side to the hypotenuse in a right triangle. |
| Tangent (tan) | tan(θ) = opposite/adjacent | Relates the angle to the ratio of the opposite side to the adjacent side in a right triangle. |
By mastering these fundamental functions and understanding how to apply them, you will be well-equipped to solve problems involving angles and distances. These functions are critical for solving many geometric and trigonometric equations, making them indispensable in your study of advanced mathematics.
Polynomial and Rational Functions Review
Understanding polynomial and rational functions is crucial for solving a wide variety of problems in advanced mathematics. These functions form the foundation for more complex topics, and being able to manipulate them correctly will greatly enhance your problem-solving skills. In this section, we will review the key characteristics, operations, and methods for working with these types of functions.
Polynomial Functions
Polynomial functions are expressions that involve terms with variables raised to non-negative integer powers. The general form of a polynomial function is a sum of terms, each consisting of a coefficient multiplied by the variable raised to a certain power. These functions are characterized by their smooth curves and predictable behavior at both ends of the graph.
- The highest power of the variable determines the degree of the polynomial.
- Polynomials can be classified as linear, quadratic, cubic, or higher-degree based on their degree.
- To find the roots or solutions of a polynomial, factoring or using the quadratic formula for lower-degree polynomials can be helpful.
Rational Functions
Rational functions are ratios of two polynomials. These functions can have asymptotes and undefined points where the denominator equals zero, so it is important to be aware of these behaviors when analyzing them. Rational functions can often be simplified, factored, or graphed similarly to polynomial functions, but they have unique characteristics that need to be considered.
- To simplify a rational function, factor both the numerator and the denominator, and cancel out any common factors.
- Vertical asymptotes occur where the denominator equals zero but the numerator does not.
- Horizontal asymptotes describe the behavior of the function as the variable approaches infinity or negative infinity.
By understanding both polynomial and rational functions, their behaviors, and how to manipulate them, you will be better equipped to tackle problems involving these types of equations in higher-level mathematics.
Exploring Exponential and Logarithmic Functions
Exponential and logarithmic functions are essential concepts that bridge various areas of mathematics and have numerous applications in real-world scenarios, such as finance, biology, and physics. These functions describe growth and decay processes and are particularly useful when dealing with situations that change rapidly over time. Understanding how to manipulate and solve problems involving these functions is key to mastering advanced mathematical topics.
Exponential functions involve a constant base raised to a variable exponent, while logarithmic functions are essentially the inverse of exponential functions. Their properties and graphs offer insights into the rates of change and help us understand exponential growth or decay.
| Function Type | General Form | Key Features |
|---|---|---|
| Exponential | f(x) = a * b^x | Describes rapid growth or decay, where ‘b’ is the base and ‘a’ is a constant multiplier. |
| Logarithmic | f(x) = log_b(x) | The inverse of exponential functions, helps solve for the exponent when the base and result are known. |
Exponential functions are commonly used to model phenomena like population growth or radioactive decay, where the change happens at a constant rate over time. Logarithmic functions, on the other hand, help reverse the process, allowing us to find unknown exponents or solve equations where the exponent is not immediately clear.
By studying the behavior of these functions and understanding their applications, you will be better equipped to solve problems that involve growth, decay, and other related processes in mathematics and beyond.
Preparation Strategies for the Apex Test
Successfully preparing for any challenging assessment requires a structured approach that focuses on reviewing key concepts, practicing problem-solving skills, and managing time effectively. By following strategic preparation methods, you can enhance your confidence and performance on the test. In this section, we will discuss effective techniques and resources to ensure you’re ready to tackle the challenges ahead.
Key Strategies for Effective Preparation
- Review the Curriculum: Focus on the core topics that are typically covered in the assessment. Review your notes, textbooks, and any study materials provided to ensure you have a solid understanding of the material.
- Practice Regularly: Consistent practice is essential for mastering concepts. Work through example problems and previous assessments to identify areas of weakness and reinforce your understanding.
- Use Online Resources: Leverage online platforms, videos, and interactive tutorials to gain different perspectives and deepen your understanding of complex topics.
- Join Study Groups: Collaborating with peers can help clarify doubts and provide new insights. Group study sessions allow you to learn from others while reinforcing your knowledge.
Time Management Tips
- Create a Study Schedule: Organize your study time by breaking down topics into manageable sections. Allocate specific times each day to focus on different areas, ensuring that you cover all the necessary material before the test.
- Prioritize Weak Areas: Spend more time on topics you find challenging, while still reviewing stronger areas to maintain your overall readiness.
- Take Regular Breaks: Avoid burnout by scheduling short breaks between study sessions. This helps improve focus and reduces mental fatigue.
By following these strategies, you can approach the test with a clear plan, adequate preparation, and a calm mindset. Remember, consistency and focus are key to success.
Using Practice Tests to Your Advantage
Practice tests are an invaluable tool for reinforcing knowledge and honing problem-solving abilities before any major assessment. By simulating the test environment, practice tests allow you to familiarize yourself with the format and types of questions you will face, helping to reduce anxiety and build confidence. Furthermore, they provide a clear picture of your strengths and areas that require additional focus, making them a critical component of a comprehensive study plan.
One of the most significant benefits of using practice tests is the ability to identify knowledge gaps. By reviewing your mistakes and understanding why you answered certain questions incorrectly, you can target specific topics for improvement. This targeted approach helps maximize study efficiency and ensures that your preparation is both thorough and effective.
In addition to improving content mastery, practice tests can also help you refine your test-taking strategies. Regular exposure to timed tests trains you to manage your time wisely during the actual assessment, ensuring that you don’t rush through questions or get stuck on challenging problems. With consistent practice, you’ll develop a rhythm that allows you to move through the material more efficiently and effectively.
To make the most of practice tests, it’s essential to treat them as real assessments. Set aside dedicated time, simulate the testing environment, and avoid distractions. After completing each test, review your results carefully, and focus on areas where you need more practice. By incorporating practice tests into your study routine, you can approach the assessment with greater assurance and preparedness.
Important Formulas to Memorize
Having a solid understanding of key formulas is essential for success in any mathematical subject. These formulas serve as the foundation for solving a variety of problems and are often used in multiple contexts. Memorizing them ensures that you can quickly apply the correct method when faced with different types of questions, saving time and reducing the chances of making errors during assessments.
While each topic may have its own set of important formulas, there are some that frequently appear across a wide range of problems. Below are some of the most crucial formulas that every student should commit to memory.
Quadratic Functions and Equations
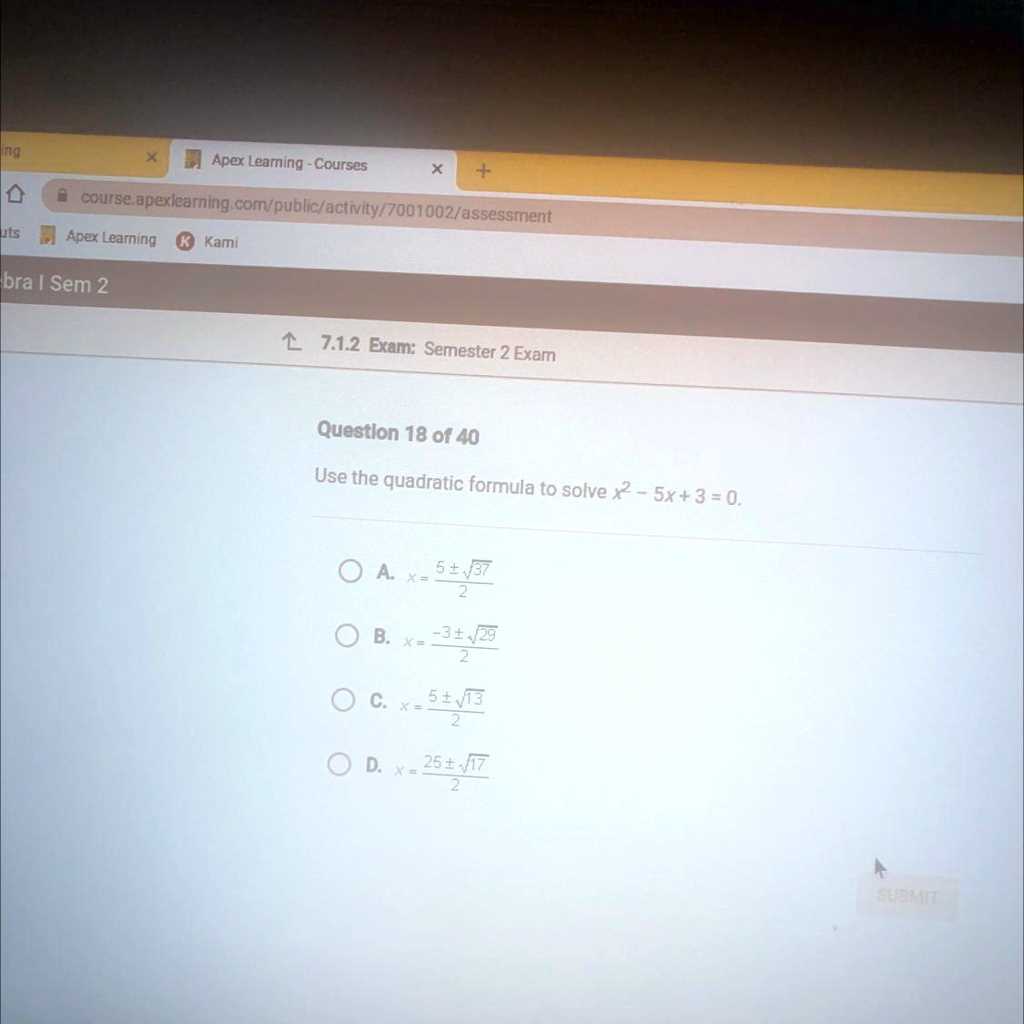
Quadratic equations are a fundamental part of advanced mathematics, and understanding their properties can help you tackle many problems. Some of the most important formulas related to quadratic functions include:
- Quadratic Formula: ( x = frac{-b pm sqrt{b^2 – 4ac}}{2a} )
- Standard Form of a Quadratic Function: ( f(x) = ax^2 + bx + c )
- Vertex Form of a Quadratic Function: ( f(x) = a(x – h)^2 + k )
Exponential and Logarithmic Functions
Exponential and logarithmic functions are also widely tested. These formulas are essential for solving problems involving growth and decay, as well as simplifying complex expressions. Here are a few key formulas:
- Exponential Growth Formula: ( y = y_0 e^{kt} )
- Logarithmic Form: ( log_b(x) = y ) if and only if ( b^y = x )
- Change of Base Formula: ( log_b(x) = frac{log_k(x)}{log_k(b)} )
Mastering these formulas, along with others specific to different topics, will not only improve your problem-solving speed but also enhance your overall understanding of the subject. Make sure to review them regularly and practice applying them to various problem types to solidify your knowledge.
How to Avoid Common Mistakes
Making errors during assessments is a common challenge, but many mistakes are preventable with the right strategies. By recognizing frequent pitfalls and knowing how to avoid them, you can improve your accuracy and efficiency. This section will explore several key areas where students often stumble and provide actionable tips for overcoming these challenges.
1. Understand the Problem Before Solving
One of the most common mistakes is jumping into solving a problem without fully understanding what it is asking. This can lead to incorrect solutions and wasted time. Take a moment to carefully read the problem, identify what is given, and determine what needs to be found. If the problem is complex, break it down into smaller parts to avoid feeling overwhelmed.
2. Double-Check Your Work
Many errors arise from simple miscalculations or oversights. Always take time to double-check your work, especially in multi-step problems. This includes reviewing your calculations, ensuring you haven’t skipped any steps, and verifying that you have applied the correct formulas or methods. A quick second look can help you catch small mistakes before finalizing your answers.
3. Stay Organized
Cluttered or disorganized work can lead to confusion and mistakes. Keep your notes, solutions, and scratch paper neat and clear. Write each step methodically and avoid rushing through the process. It’s easier to spot mistakes in well-organized work, and it helps you stay focused on the task at hand.
4. Practice Common Problem Types
Repetition is key to mastering any subject. By practicing common problem types regularly, you become familiar with the techniques required to solve them correctly. This will increase your confidence and decrease the likelihood of making mistakes under pressure.
By applying these strategies, you can minimize errors and improve your overall performance. Remember, the goal is not just to get the correct answer but to develop a systematic approach that allows you to solve problems accurately and efficiently every time.
Utilizing Online Resources for Help
In the digital age, the internet offers a wealth of resources that can be incredibly valuable when it comes to studying and understanding complex topics. Whether you’re struggling with specific concepts or just looking for a different perspective on a problem, there are numerous tools and platforms that can help you enhance your learning experience. This section highlights how you can leverage online resources to your advantage, ensuring that you get the support you need to succeed.
1. Educational Websites
Many websites are designed to offer comprehensive tutorials, practice problems, and step-by-step solutions. These platforms can help clarify difficult concepts and provide additional examples to strengthen your understanding. Some popular sites include:
- Khan Academy: Offers free, detailed video lessons on a wide range of topics, along with exercises to test your knowledge.
- Wolfram Alpha: A powerful computational tool that can solve mathematical problems and explain the steps behind the solution.
- PatrickJMT: Provides clear and concise math tutorials, especially for high school and college-level topics.
2. Online Forums and Study Groups
If you’re looking for help from peers or experts, online forums and study groups can be invaluable. These platforms allow you to ask questions, share knowledge, and engage in discussions that can deepen your understanding. Popular forums include:
- Reddit: Subreddits like r/learnmath and r/MathHelp provide communities where users can ask questions and receive answers from experienced individuals.
- Stack Exchange: Offers a Q&A format for math-related queries, where experts and learners alike contribute to problem-solving.
3. Educational Videos
For visual learners, YouTube is an excellent source for educational content. Channels dedicated to explaining mathematical concepts often offer tutorials and problem-solving sessions that can break down even the most complex topics. Some well-regarded channels include:
- Professor Leonard: Offers detailed lectures and tutorials that walk through various math topics with clear explanations.
- 3Blue1Brown: Uses animations and visualizations to explain abstract mathematical ideas, making them easier to grasp.
By utilizing these online resources, you can access a wealth of information and get the help you need to overcome any challenges. Whether through structured lessons, interactive forums, or visual explanations, the internet provides numerous tools to help reinforce your understanding and boost your confidence.
Why Understanding Concepts is Crucial
Grasping the underlying principles behind mathematical topics is essential for long-term success. Simply memorizing formulas or procedures without understanding their meaning can lead to confusion and difficulty when faced with complex problems. A deep comprehension of the core concepts allows students to approach new challenges with confidence and flexibility, enabling them to apply their knowledge in various contexts. This section discusses why focusing on understanding, rather than just rote memorization, is key to mastering the subject.
1. Building a Strong Foundation
When you understand the “why” behind a concept, you’re able to build a strong foundation that supports more advanced topics. Each new idea in mathematics often builds upon previous knowledge. Without a clear understanding of the fundamentals, it becomes difficult to grasp more complex topics. This is why focusing on conceptual learning from the start is essential. Understanding allows for smoother transitions into advanced concepts and better retention over time.
2. Problem-Solving Flexibility
Having a solid grasp of the core ideas means you can adapt to different types of problems. If you only memorize steps without understanding their purpose, you may struggle when problems are presented in unfamiliar ways. On the other hand, understanding the logic behind mathematical methods enables you to recognize patterns, identify key principles, and apply them to new problems effectively.
Ultimately, understanding concepts provides the foundation for both immediate success and future learning. It helps you think critically, solve problems efficiently, and build the skills necessary for tackling increasingly complex topics with confidence.
Tips for Staying Calm During the Test
Managing stress and staying composed during a timed assessment is crucial for performing well. Anxiety can often cloud your judgment, making it harder to recall information and focus on the tasks at hand. Knowing how to stay calm and approach the situation with a clear mind can significantly improve your chances of success. In this section, we’ll explore effective strategies to keep your nerves in check and maintain a focused mindset throughout the test.
1. Practice Deep Breathing
When you feel overwhelmed, taking a few deep breaths can help you regain control of your emotions. Deep breathing encourages relaxation by slowing your heart rate and reducing anxiety. Try inhaling deeply for four seconds, holding for four seconds, and exhaling for four seconds. Repeating this process can help you calm down and refocus your mind on the task at hand.
2. Manage Your Time Effectively
One of the main sources of stress during assessments is the pressure of running out of time. To avoid this, it’s important to pace yourself. Begin by quickly reviewing the entire test and identifying questions you can easily answer first. This will build confidence and save time for more challenging problems. Set mini-deadlines for each section, and if you get stuck on a question, move on and come back to it later. This strategy helps you avoid spending too much time on a single question while ensuring that you complete the entire test.
By incorporating these strategies into your preparation and during the test itself, you can stay calm and focused, allowing you to perform at your best. Remember that managing stress is a skill that improves with practice, so use every opportunity to refine your approach and gain confidence in your abilities.