
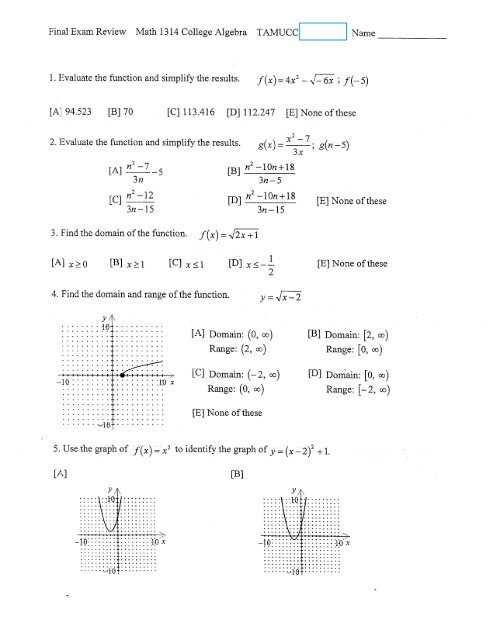
Preparing for a challenging assessment requires a solid understanding of the core principles and strategies used in various mathematical topics. This section will help reinforce your grasp of the key areas that are likely to appear on the test. By focusing on essential concepts and techniques, you can approach the questions with confidence and clarity.
Mastering fundamental skills is the first step towards excelling. Whether it’s working with equations, simplifying expressions, or interpreting graphs, these skills form the backbone of problem-solving. A clear understanding of the underlying theories allows you to apply the right approach to a wide range of problems.
As you review different types of exercises, it’s important to recognize patterns and understand the logic behind each step. The more familiar you become with these patterns, the more efficient you will be at solving problems quickly and accurately.
Mathematics Assessment Preparation and Solutions
Successfully tackling a complex test requires more than just memorization of formulas. It’s about developing a deep understanding of how mathematical concepts work together. By focusing on core topics and practicing problem-solving techniques, you can increase both your accuracy and speed during the assessment.
Key Concepts to Focus On
Make sure you have a solid grasp of the critical areas that are often tested. From solving equations and inequalities to working with polynomials, mastering these subjects is crucial. Understanding how to manipulate variables and interpret results will give you the tools to approach a wide range of questions with confidence.
Effective Problem-Solving Techniques

In addition to understanding the theories, it’s essential to be familiar with the methods for solving problems quickly and accurately. Start by identifying the type of problem you’re dealing with, then apply the appropriate steps. With consistent practice, these techniques will become second nature, allowing you to handle even the most complex questions efficiently.
Practice is key to reinforcing your knowledge. The more problems you work through, the better prepared you will be to face the real challenge. Use available resources to test your skills and identify areas that need improvement. By approaching each practice session with a strategic mindset, you’ll be able to master even the most challenging topics.
Understanding Key Concepts for Algebra 2
Grasping the foundational principles of mathematics is essential for success in more advanced problem-solving tasks. Focusing on understanding key relationships between numbers and variables will allow you to solve equations and interpret functions with ease. Mastery of these concepts enables you to approach complex scenarios confidently and accurately.
Fundamental Principles of Equations
One of the first steps in mastering these mathematical ideas is understanding how to work with different types of equations. This includes linear, quadratic, and rational forms. Knowing how to isolate variables, simplify expressions, and apply the right methods will help you efficiently solve for unknowns and interpret results correctly.
Working with Functions and Graphs
Another core area to focus on is understanding functions and their graphical representations. Knowing how to plot points, identify slopes, and interpret intercepts is crucial for analyzing mathematical relationships. By connecting algebraic expressions to their visual counterparts, you can deepen your comprehension and make solving real-world problems easier.
Consistent practice with these concepts is the best way to build confidence. The more familiar you become with these fundamental skills, the more quickly you’ll recognize patterns and apply techniques to a variety of problems. Keep reinforcing your knowledge, and you’ll find it easier to navigate complex mathematical challenges.
Critical Topics to Focus On
When preparing for a challenging assessment, it’s important to prioritize the most essential topics that will likely make up a significant portion of the test. By honing in on these areas, you can maximize your study time and ensure that you are fully prepared to tackle the most common problem types. Understanding these key concepts will give you the tools needed to approach a variety of questions with confidence.
Mastering Quadratic Equations and Functions

Quadratic equations and functions are among the most frequently tested topics. Knowing how to solve these equations using various methods such as factoring, completing the square, or applying the quadratic formula is critical. Additionally, understanding how to graph these functions and identify key features like the vertex and axis of symmetry is crucial for interpreting their behavior and solving related problems.
Polynomials and Factoring Techniques
Working with polynomials is another vital skill. This involves simplifying expressions, performing long division, and factoring different forms of polynomials. Mastering the distributive property and understanding the relationships between coefficients and exponents will allow you to manipulate polynomial expressions efficiently and solve problems with ease.
Concentrating on these core topics will help you solidify your understanding and give you a strong foundation for solving more complex problems. With enough practice, these areas will become second nature, making your problem-solving process more streamlined and effective.
How to Approach Word Problems
Word problems often seem intimidating because they require translating real-world scenarios into mathematical expressions. However, breaking down the problem into manageable steps makes it much easier to find the solution. By carefully reading the problem, identifying key information, and applying the appropriate techniques, you can successfully tackle these types of questions.
The first step is to carefully read the problem and highlight important details, such as given values and the question being asked. Next, translate these details into a mathematical format, whether it be an equation or a set of relationships. Once the problem is in a manageable form, you can proceed with solving it using the appropriate method.
| Step | Action |
|---|---|
| 1 | Read the problem carefully and highlight key information. |
| 2 | Identify the mathematical relationships and translate the text into an equation. |
| 3 | Solve the equation step by step, checking each step for accuracy. |
| 4 | Review the solution and make sure it answers the question asked. |
Practice is essential for becoming proficient at solving word problems. The more you practice, the more quickly you’ll recognize patterns and apply the right strategies to solve them efficiently.
Mastering Quadratic Equations and Functions
Quadratic equations and their related functions are fundamental concepts that appear frequently in mathematical problem-solving. To successfully navigate these problems, it’s crucial to understand the different methods for solving and graphing them. By developing a strong grasp of key techniques, you can solve equations with confidence and interpret their graphical representations accurately.
Solving Quadratic Equations
There are several methods for solving quadratic equations, each of which is useful depending on the situation. The most common techniques include:
- Factoring: Expressing the equation as a product of binomials.
- Completing the square: Manipulating the equation to form a perfect square trinomial.
- Quadratic formula: Applying the formula x = (-b ± √(b² – 4ac)) / 2a to find the roots.
Graphing Quadratic Functions
The graph of a quadratic function is a parabola. Understanding its key features will help you interpret the function effectively. Key aspects to focus on include:
- Vertex: The point where the parabola changes direction.
- Axis of symmetry: A vertical line passing through the vertex that divides the parabola into two symmetric halves.
- Roots (or x-intercepts): The points where the graph intersects the x-axis.
Practice these techniques regularly to become proficient in both solving and graphing quadratic equations. The more you work through these types of problems, the easier it will be to recognize patterns and apply the correct methods quickly and accurately.
Simplifying Expressions with Exponents
Working with exponents requires understanding the rules that govern their manipulation. Simplifying expressions involving powers can make complex problems much easier to solve. By applying basic exponent rules, you can reduce complicated terms and find solutions more efficiently.
Key Exponent Rules
To simplify expressions with exponents, it’s essential to know the core rules that apply. These include:
- Product Rule: a^m × a^n = a^(m+n)
- Quotient Rule: a^m ÷ a^n = a^(m-n)
- Power Rule: (a^m)^n = a^(m×n)
- Negative Exponent Rule: a^(-n) = 1/a^n
- Zero Exponent Rule: a^0 = 1
Steps for Simplifying Expressions
To simplify an expression with exponents, follow these steps:
- Identify and group like terms with the same base.
- Apply the appropriate exponent rule to combine the terms.
- Simplify the resulting expression, making sure to reduce fractions or terms when necessary.
Practice these steps regularly to become more efficient in simplifying complex expressions. The more you apply these rules, the easier it will be to recognize which technique to use in different situations.
Solving Systems of Equations Efficiently
Solving systems of equations is a critical skill for tackling multi-variable problems. Whether you’re working with two or more equations, knowing how to approach them systematically will help you find the solutions more efficiently. There are various methods available, each suited to different types of systems, and mastering these will ensure quicker and more accurate results.
Common Methods for Solving Systems
The main approaches for solving systems of equations are:
- Substitution Method: Solving one equation for a variable and then substituting that expression into the other equation.
- Elimination Method: Adding or subtracting equations to eliminate one variable, making it easier to solve for the other.
- Graphical Method: Plotting both equations on a graph and finding the point where the lines intersect.
Steps to Solve Using Substitution and Elimination
Here’s a simple guide on how to apply these methods:
| Method | Steps |
|---|---|
| Substitution | 1. Solve one equation for a variable. 2. Substitute that expression into the other equation. 3. Solve for the remaining variable. |
| Elimination | 1. Multiply or divide equations to align coefficients. 2. Add or subtract the equations to eliminate one variable. 3. Solve for the remaining variable. |
Practice these methods to improve your ability to solve systems quickly. With regular use, these techniques will become second nature, allowing you to solve even complex systems more efficiently and accurately.
Working with Polynomials and Factoring
Manipulating polynomials and factoring them efficiently is an essential skill in solving various mathematical problems. By breaking down complex expressions into simpler components, you can easily simplify or solve equations. Understanding the core techniques for working with polynomials and their factorizations will make handling these problems much more straightforward.
Key Techniques for Working with Polynomials
When dealing with polynomials, there are several fundamental operations and methods to keep in mind:
- Adding and Subtracting Polynomials: Combine like terms by adding or subtracting their coefficients.
- Multiplying Polynomials: Apply the distributive property or use the FOIL method for binomials.
- Dividing Polynomials: Use long division or synthetic division to divide one polynomial by another.
Factoring Polynomials
Factoring polynomials is the process of breaking them down into simpler expressions, often to solve equations. Common methods include:
- Factoring by GCF (Greatest Common Factor): Find the largest common factor and factor it out of the polynomial.
- Factoring Trinomials: Look for two binomials that multiply to give the original trinomial.
- Factoring Difference of Squares: Recognize when a polynomial is in the form of a² – b² and factor it as (a + b)(a – b).
- Factoring by Grouping: Split the polynomial into groups and factor each group separately.
Mastering these methods will help you simplify polynomials quickly and solve equations more efficiently. With consistent practice, factoring will become an intuitive process, allowing you to approach complex problems with ease.
Tips for Graphing Rational Functions
Graphing rational functions can be challenging, but understanding key features and behaviors will make the process more manageable. By analyzing asymptotes, intercepts, and critical points, you can plot a precise and accurate graph. With the right techniques, graphing these functions becomes more systematic and less overwhelming.
Key Features to Identify

Before plotting a rational function, it’s essential to identify the following key components:
- Vertical Asymptotes: These occur where the denominator equals zero but the numerator is non-zero. They represent values that the function approaches but never crosses.
- Horizontal Asymptotes: The horizontal line that the function approaches as x approaches positive or negative infinity.
- Intercepts: Find the x-intercepts by setting the numerator equal to zero, and the y-intercept by evaluating the function at x = 0.
Steps for Graphing Rational Functions
To graph a rational function, follow these steps:
- Factor both the numerator and denominator to simplify the function if possible.
- Identify vertical and horizontal asymptotes.
- Find intercepts by setting x and y to zero as necessary.
- Plot additional points, considering the function’s behavior near the asymptotes.
- Connect the points, taking care to reflect the function’s behavior at key features.
By following these steps, you can accurately graph rational functions. Regular practice will improve your ability to recognize the behavior of these functions quickly, making graphing more intuitive over time.
Key Strategies for Solving Inequalities

Solving inequalities involves finding the set of values that satisfy a given condition. Unlike equations, inequalities represent a range of possible solutions rather than a single value. Understanding the key strategies for solving inequalities is crucial for accurately determining solution sets and graphing their representations on a number line.
Steps for Solving Inequalities
When solving inequalities, it’s important to follow a consistent approach. Here are the main steps to keep in mind:
- Isolate the Variable: Just like in equations, begin by isolating the variable on one side of the inequality sign. This often involves addition, subtraction, multiplication, or division.
- Flip the Inequality Sign: When multiplying or dividing both sides of an inequality by a negative number, remember to reverse the direction of the inequality symbol.
- Graph the Solution: Once you’ve solved for the variable, represent the solution on a number line. Use open or closed circles depending on whether the inequality is strict (<, >) or inclusive (≤, ≥).
Important Considerations
Keep these important points in mind as you work through inequalities:
- Compound Inequalities: Solve compound inequalities by treating them as two separate inequalities and then finding the common solution set.
- Rational Inequalities: When dealing with rational expressions, be careful to account for restrictions on the domain where the denominator is zero.
By mastering these strategies, solving inequalities will become more straightforward. With practice, you’ll be able to approach problems with confidence and determine solution sets efficiently.
Recognizing Patterns in Sequences
Recognizing patterns in sequences is a vital skill that helps in solving a variety of mathematical problems. Sequences often follow a specific rule or relationship, which can be identified through careful observation. Once the pattern is recognized, it becomes easier to predict future terms or derive formulas for the sequence. Understanding how to spot these patterns is key to working efficiently with sequences in any mathematical context.
Common Types of Patterns
Sequences can follow different types of patterns. Below are some of the most common ones:
- Arithmetic Sequences: These sequences have a constant difference between consecutive terms. The common difference is added or subtracted to generate the next term.
- Geometric Sequences: In these sequences, each term is multiplied by a constant ratio to obtain the next term.
- Fibonacci Sequence: Each term is the sum of the two preceding ones, starting from 0 and 1.
- Quadratic Sequences: These sequences follow a pattern where the second difference between consecutive terms is constant.
Identifying and Extending Patterns
To recognize and extend patterns in sequences, follow these steps:
- Look for Consistency: Observe the differences between terms or the ratios between successive numbers to identify the type of sequence.
- Write a General Rule: Once you identify the pattern, try to express it as a formula or rule that can be applied to find any term in the sequence.
- Test the Rule: Apply the rule to several terms in the sequence to ensure it holds true.
- Predict Future Terms: Use the rule to predict subsequent terms in the sequence.
By mastering the identification of patterns, you’ll be able to tackle sequence-related problems more effectively. This skill is essential for solving problems that involve series, recurrence relations, and many other topics in mathematics.
Understanding the Unit Circle and Trigonometry
The unit circle is a fundamental concept that underpins many aspects of trigonometry. It provides a visual way to understand the relationships between angles and the corresponding values of trigonometric functions. By using a circle with a radius of one unit, key values for sine, cosine, and tangent can be easily identified, allowing for a more intuitive approach to solving problems in geometry, physics, and engineering.
At its core, the unit circle connects angular measure with the lengths of the sides of right triangles. Each point on the circle corresponds to an angle, and the coordinates of that point give the values of sine and cosine. By understanding this relationship, one can efficiently calculate trigonometric values and solve complex problems involving angles and lengths.
Key Components of the Unit Circle

The unit circle has several important features that help in solving trigonometric equations:
- Radius: The radius of the unit circle is always 1, which simplifies calculations and allows for easy reference of trigonometric values.
- Angles: Angles are typically measured in radians, with 360° corresponding to 2π radians. Positive angles represent counterclockwise rotation, while negative angles represent clockwise rotation.
- Coordinates: The coordinates of any point on the unit circle can be written as (cos(θ), sin(θ)), where θ is the angle formed with the positive x-axis.
Using the Unit Circle in Trigonometry
With the unit circle, trigonometric functions such as sine, cosine, and tangent can be calculated for any given angle:
- Sine (sin): The sine of an angle is the y-coordinate of the corresponding point on the unit circle.
- Cosine (cos): The cosine of an angle is the x-coordinate of the corresponding point on the unit circle.
- Tangent (tan): The tangent of an angle can be found by dividing the sine by the cosine, or equivalently, tan(θ) = sin(θ)/cos(θ).
Mastering the unit circle allows for greater ease in solving trigonometric problems, as it provides a consistent framework for understanding the relationships between angles and trigonometric functions. Whether working with standard angles or solving more complex trigonometric identities, the unit circle is an invaluable tool in the study of mathematics.
Reviewing Radical Expressions and Equations
Understanding the manipulation and simplification of expressions involving roots is essential for tackling more advanced mathematical concepts. These expressions, which often involve square roots, cube roots, or higher powers, require specific techniques for simplifying, solving, and transforming them into more manageable forms. Mastery of radical operations allows for a more thorough understanding of complex equations and inequalities.
Radical expressions are typically simplified by factoring out perfect squares or cubes, simplifying the terms under the root, and performing operations on the exponents. Solving equations involving radicals involves isolating the radical term and squaring or cubing both sides, depending on the type of root involved. However, care must be taken to check for extraneous solutions that may arise from these operations.
Key Techniques for Simplifying Radical Expressions
When simplifying radical expressions, several important steps can help ensure the solution is as simplified as possible:
- Identifying Perfect Squares or Cubes: Recognizing perfect squares or cubes within the radical allows for immediate simplification. For example, √36 simplifies to 6 because 36 is a perfect square.
- Factorizing Under the Radical: Factor out any perfect powers from under the radical. For example, √(8) can be rewritten as √(4 × 2), which simplifies to 2√2.
- Rationalizing the Denominator: If a fraction has a radical in the denominator, multiply both the numerator and denominator by the appropriate radical to eliminate the radical from the denominator.
Solving Radical Equations
To solve equations involving radicals, it’s often necessary to follow a systematic approach:
- Isolate the Radical: Begin by isolating the radical expression on one side of the equation to make the next step more straightforward.
- Eliminate the Radical: Depending on the type of radical, square or cube both sides of the equation to remove the root. For example, squaring both sides of √x = 5 gives x = 25.
- Check for Extraneous Solutions: Always check your solutions by substituting them back into the original equation. Sometimes, squaring or cubing both sides can introduce extraneous solutions that do not actually satisfy the original equation.
By mastering these techniques, solving radical expressions and equations becomes a more efficient and systematic process, providing a strong foundation for more complex mathematical challenges.
Common Mistakes to Avoid on the Exam
Many students face challenges when solving mathematical problems under time pressure. To ensure success, it is crucial to be aware of common errors that can lead to unnecessary mistakes. Recognizing and avoiding these pitfalls can make a significant difference in achieving better results. While solving problems, careful attention to detail is necessary to avoid missteps that might otherwise be overlooked in the rush of an assessment.
Some mistakes are easy to overlook, such as misinterpreting a question, neglecting to simplify expressions, or making calculation errors. Additionally, failing to check your work or skipping important steps can also result in avoidable mistakes. Keeping a clear, methodical approach will help mitigate these errors and ensure you approach each problem confidently and accurately.
Key Mistakes to Watch Out For
Here are some of the most frequent mistakes that students make when tackling mathematical problems:
- Not Simplifying Expressions: Many students fail to simplify their answers fully. Always check if you can reduce fractions, simplify square roots, or combine like terms.
- Incorrectly Handling Signs: Be mindful of signs, especially when dealing with negative numbers or variables. A common mistake is overlooking negative signs during multiplication or division.
- Forgetting to Check Solutions: After solving an equation, make sure to substitute your solution back into the original equation to ensure it’s correct and not extraneous.
- Skipping Steps: In an effort to save time, students often skip intermediate steps, which can lead to mistakes. Show all steps clearly to ensure you don’t miss anything.
- Misinterpreting Word Problems: Carefully read word problems and ensure you fully understand what is being asked before starting to solve. Breaking down the information into smaller parts can help.
Tips to Avoid These Mistakes
To avoid these common mistakes, follow these strategies:
| Tip | Description |
|---|---|
| Work Slowly and Carefully | Rushing through problems increases the likelihood of simple mistakes. Take your time to review each step. |
| Double-Check Your Work | After completing a problem, revisit your solution to ensure all steps are correct, especially the final answer. |
| Stay Organized | Write neatly, and clearly organize your work to avoid confusion during problem-solving. |
| Practice Regularly | The more practice you get, the more familiar you will become with common problem types and how to solve them efficiently. |
By staying focused and being mindful of these mistakes, you can approach each problem with confidence and avoid costly errors during assessments.
Time Management During the Exam
Efficient time management is essential when tackling any timed assessment. Being able to allocate time effectively across different tasks is key to ensuring you can complete each question with care and still have time to review your work. Proper planning and pacing allow you to focus on both accuracy and completion without rushing through problems or leaving some unanswered.
One of the main challenges students face is managing time under pressure. Without a clear strategy, it can be easy to get stuck on a difficult question and lose track of time. However, by adopting a systematic approach to time allocation, you can reduce stress and improve performance. The key is knowing how much time to spend on each section and how to move efficiently between different types of questions.
Effective Time Management Tips
- Read Through the Entire Assessment: Before starting, take a few minutes to quickly read through all the questions. This gives you an overview of what to expect and helps you identify any particularly challenging sections that may need more time.
- Prioritize Easier Questions: Begin with the questions that you find easier or are more familiar with. This allows you to gain confidence and save time for the more difficult ones later.
- Set Time Limits for Each Question: Set a specific time limit for each question or section based on its complexity. Stick to this time limit to ensure you have enough time to attempt all questions.
- Don’t Get Stuck: If you encounter a difficult question, don’t spend too much time on it. Move on to the next one and return to the challenging question later, if time allows.
- Use Time Wisely During the Final Minutes: In the last 10–15 minutes, review your answers. Look for obvious errors, and if you have time, try to rework any questions you found difficult.
Sample Time Allocation Strategy
- Start with a quick scan of the entire paper to see the number of questions.
- For a 60-minute assessment with 30 questions, aim to spend about 1–2 minutes per question, adjusting for the difficulty.
- If there are multiple-choice questions, allocate less time to these and more time for problem-solving sections.
- Leave 10–15 minutes at the end to double-check your work.
By managing your time carefully, you can reduce anxiety, increase productivity, and ensure that you have enough time to address every part of the assessment, maximizing your chances of success.
Effective Use of Calculators
Calculators are powerful tools that can help simplify complex problems, allowing you to focus more on problem-solving techniques and understanding key concepts. However, to make the most of a calculator during a timed assessment, it is important to use it efficiently and strategically. Knowing when and how to rely on the calculator can save you time and improve the accuracy of your results.
While calculators can quickly handle basic operations, their true value lies in their ability to assist with more intricate calculations such as solving equations, graphing functions, and performing statistical analysis. The key is understanding the features of your calculator and how to apply them to different types of problems. Proper use of a calculator can minimize errors and help you complete more problems within the allotted time.
Tips for Maximizing Calculator Use
- Know Your Calculator: Familiarize yourself with all the functions of your calculator, including solving equations, graphing, and using memory functions. Take time to learn how to navigate the settings and shortcuts before the assessment.
- Use the Calculator for Repetitive Calculations: For problems that require repetitive computations (like multiplication or division), let the calculator handle the work to save time.
- Verify Your Work: Use the calculator to double-check your manual calculations, especially when dealing with large numbers or complex fractions.
- Leverage Graphing Capabilities: For problems involving equations or inequalities, graphing them on a calculator can help you visually analyze the behavior of the functions and find solutions more efficiently.
- Avoid Over-reliance: While calculators are helpful, ensure that you still understand the underlying principles. Relying too much on the calculator can prevent you from developing the necessary problem-solving skills.
Examples of When to Use a Calculator
- Solving Quadratic Equations: Use your calculator to solve quadratic equations using the quadratic formula or by graphing the equation to find the roots.
- Working with Large Numbers: For problems involving large multiplications, divisions, or powers, let the calculator handle the heavy lifting to avoid errors.
- Graphing Functions: If you’re working with a complex function, use the graphing tool to visualize the behavior of the equation and identify key features like intercepts and asymptotes.
- Performing Statistical Calculations: Use the calculator’s statistical functions to find mean, median, mode, and standard deviation, saving you time compared to doing these manually.
By using your calculator effectively, you can work more efficiently, improve accuracy, and have more time to focus on understanding the problem-solving process. Proper use of this tool can make a significant difference in your overall performance.
Study Resources and Practice Problems
Having access to the right materials and consistently practicing problems is crucial for mastering mathematical concepts. Utilizing various resources will help reinforce your understanding and improve your problem-solving skills. The key is to make use of diverse tools that offer both theoretical explanations and practical exercises, ensuring a well-rounded preparation.
In addition to textbooks and class notes, there are numerous online platforms, worksheets, and problem sets available to help you practice. These resources allow you to work through problems at your own pace, review difficult topics, and track your progress. Engaging with different types of problems can help you become more comfortable with various methods of solving and analyzing mathematical situations.
Useful Resources for Practice

- Online Math Platforms: Websites like Khan Academy, Brilliant, and Mathway offer tutorials, videos, and practice questions that cover a wide range of topics. These platforms often provide step-by-step solutions to help you understand the processes behind each problem.
- Textbooks and Workbooks: Your course textbook may include additional practice problems and solutions. Workbooks dedicated to specific topics often provide extra exercises for honing your skills.
- Interactive Apps: Apps like Wolfram Alpha or Desmos provide interactive problem-solving tools that allow you to graph functions, solve equations, and explore various mathematical concepts visually.
- Study Groups: Collaborating with classmates or peers can be an excellent way to exchange knowledge, discuss difficult problems, and test each other’s understanding.
Sample Practice Problems
Here are some examples of common types of problems that you should practice:
| Problem Type | Sample Problem | Solution Approach |
|---|---|---|
| Linear Equations | 2x + 5 = 15 | Solve for x by isolating the variable and performing basic arithmetic operations. |
| Quadratic Equations | x² – 6x + 8 = 0 | Use factoring, completing the square, or the quadratic formula to find the roots. |
| Graphing Functions | Graph y = 2x – 3 | Plot the equation on a graph by identifying the slope and y-intercept. |
| Word Problems | A car travels 60 miles in 1.5 hours. What is its average speed? | Divide distance by time to find the speed (Speed = Distance / Time). |
| Systems of Equations | y = 3x + 4 and y = -x + 2 | Set the equations equal to each other and solve for x, then substitute back to find y. |
By regularly practicing these types of problems, you will develop the skills needed to approach similar questions confidently and efficiently. The more you engage with varied problems, the better prepared you will be for any challenge you face.
How to Stay Calm During the Test
Remaining composed during a high-pressure situation is essential for performing well. It’s natural to feel anxious, but learning to manage that stress can significantly enhance focus and effectiveness. Maintaining a calm mindset allows you to think clearly, solve problems more efficiently, and avoid making unnecessary mistakes.
Start by adopting deep breathing techniques or mindfulness exercises before the test. Taking a few slow, deep breaths can help reduce anxiety and ground you in the present moment. It’s also helpful to practice staying calm before the actual test, by simulating test conditions at home or with practice problems, so you can better handle the real experience.
Another effective strategy is time management. By allocating a set amount of time to each question and moving forward without dwelling on tough problems, you can prevent frustration from building. If you find yourself stuck on a question, it’s often better to skip it and return later with a fresh perspective.
Additionally, keeping a positive attitude can influence your mental state. Focus on what you do know, and remind yourself that it’s okay if you don’t have all the answers right away. Confidence in your preparation will allow you to approach each problem with a calm, logical mindset.
Finally, remember that test conditions are temporary, and staying composed will help you make the most of your knowledge and abilities. If you practice these techniques regularly, you will develop a stronger sense of control during any high-stakes situation.