
Mastering mathematical assessments requires both understanding the core principles and developing effective problem-solving strategies. These assessments often test your ability to apply various concepts and theories in practical scenarios, where precision and reasoning play crucial roles. A strong foundation in key topics will help you approach any problem with confidence and clarity.
With the right preparation, you’ll be able to navigate through complex tasks, making logical connections between different topics. Whether you’re tackling algebraic equations, geometric constructions, or abstract problem-solving challenges, every question tests your understanding and ability to synthesize knowledge.
In this guide, we will break down essential techniques and solutions to help you succeed. From step-by-step explanations to time-saving tips, each section is designed to build your skills and provide clarity. By the end, you’ll have a comprehensive understanding of how to tackle advanced math challenges effectively.
Geometry CCSS Regents Exam 0817 Answers
Preparing for a comprehensive mathematics test requires understanding both the concepts and the specific problem types that frequently appear. Focusing on problem-solving techniques, logical reasoning, and accurate execution will help you navigate through even the most challenging questions. This section provides a breakdown of common problem types and effective strategies for solving them.
Here are some key aspects to keep in mind when tackling advanced mathematics problems:
- Understanding the instructions: Ensure that you fully comprehend what each question is asking before proceeding with the solution.
- Reviewing critical formulas: Memorizing essential formulas and knowing when to apply them is vital for solving various types of problems.
- Strategic problem-solving: Approach each question step by step, breaking it down into smaller, manageable parts.
By focusing on these strategies, you can effectively work through the various challenges presented in the assessment. Success comes from a combination of preparation, practice, and time management skills. Below are additional tips to help maximize your performance:
- Stay organized: Keep your work neatly arranged and write out all steps to avoid making careless mistakes.
- Time management: Allocate enough time to each section, leaving a few minutes at the end for review.
- Practice regularly: Consistent practice with different problem sets is key to building confidence and efficiency.
Following these guidelines will help improve your performance and ensure that you’re well-prepared for tackling advanced mathematical problems with confidence.
Understanding the Geometry Regents Exam Format

Familiarity with the structure of a mathematical assessment is essential for effective preparation. Knowing the format allows you to allocate time properly and focus on the areas that matter most. A typical assessment of this kind is divided into distinct sections that test various problem-solving skills, from multiple-choice questions to more complex, open-ended problems.
The test generally consists of two main parts: one focusing on basic computation and understanding of fundamental principles, and another requiring in-depth application of these concepts in more complex scenarios. The first part is usually faster-paced and includes straightforward questions, while the second part tests deeper knowledge and problem-solving abilities, often involving multi-step processes.
In addition to the question types, it is important to be aware of the time constraints. While there are usually enough minutes to complete the test, managing time effectively ensures that you don’t rush through questions or leave any unanswered. Knowing the format ahead of time helps you to stay calm and organized during the assessment.
Key Topics Covered in CCSS Geometry
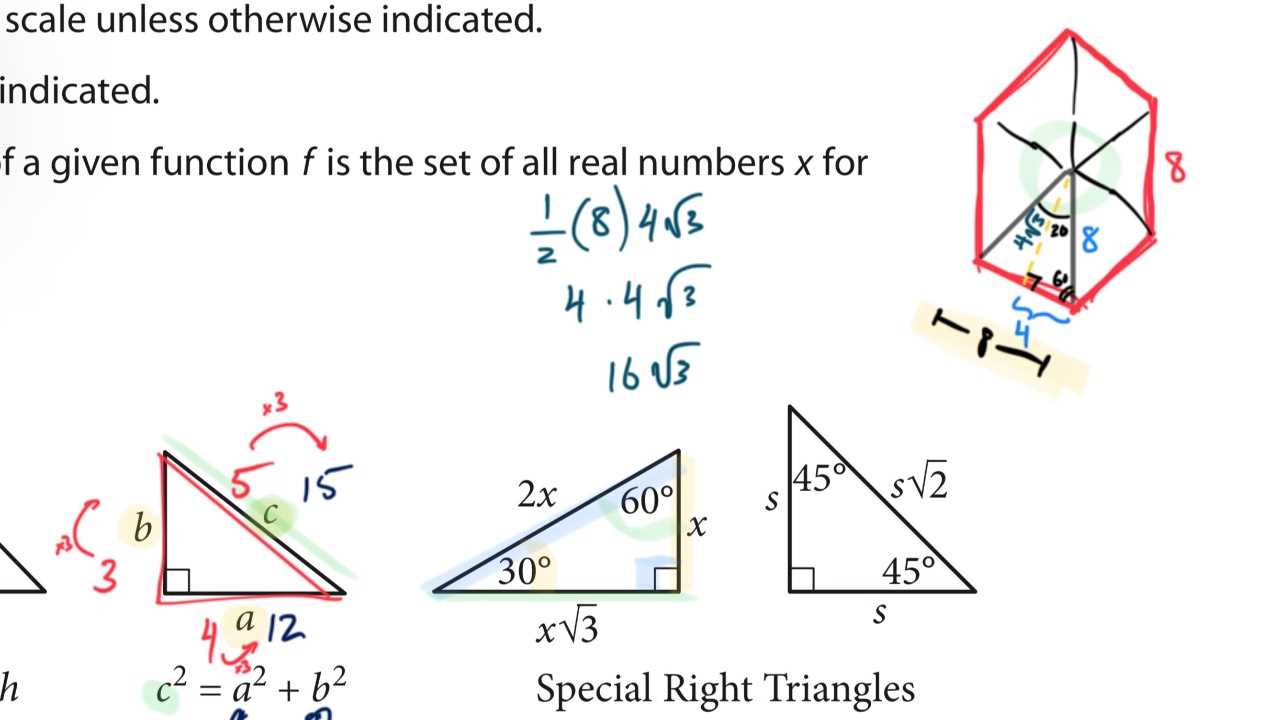
In any advanced mathematical assessment, a variety of critical topics are tested. These topics are designed to assess your understanding of both foundational concepts and their application in more complex scenarios. Mastery of these areas is crucial to performing well in the test, as they frequently appear in different forms and require diverse problem-solving strategies.
Basic Concepts and Principles

One of the fundamental areas covered includes basic concepts such as shapes, angles, and lines. Understanding properties like congruency, similarity, and symmetry is essential for solving a wide range of problems. Additionally, familiarity with key definitions and postulates will allow you to approach questions with confidence and clarity.
Advanced Applications and Theorems
The more advanced topics often involve applying these core principles to solve complex problems. This includes working with geometric proofs, transformations, and coordinate geometry. You’ll need to use logical reasoning to link different concepts and demonstrate a comprehensive understanding of the material. Problem-solving in these areas often requires multiple steps and a strategic approach to arrive at the correct solution.
How to Approach Geometry Questions Effectively
When tackling advanced mathematical problems, having a clear strategy is essential. A structured approach helps ensure that you fully understand the question, break it down into manageable parts, and apply the right techniques to reach the solution. Success in these types of assessments is not just about knowing formulas but also about being able to apply them effectively in different scenarios.
Start by carefully reading the problem: Ensure you understand exactly what is being asked before jumping into calculations. Identify key information such as given values, conditions, and what needs to be determined. Often, the most important clues are hidden in the wording.
Visualize the problem: Drawing diagrams or graphs can help clarify complex relationships and give you a visual reference. This is especially helpful when working with shapes, angles, or coordinate-based problems. A quick sketch can sometimes make the solution much clearer.
Break down the steps: Divide the problem into smaller, more manageable parts. Tackling one step at a time makes it easier to avoid errors and ensures that you don’t overlook crucial details. Keep track of each step logically, and double-check your work as you proceed.
By following these strategies, you will improve your ability to solve problems accurately and efficiently. Clear thinking, organization, and patience are key components to success in advanced mathematical challenges.
Step-by-Step Solutions for 0817 Exam
Breaking down complex problems into simple, manageable steps is key to mastering any challenging assessment. By understanding each part of the problem and solving it methodically, you increase your chances of arriving at the correct solution. This approach not only reduces errors but also helps you stay organized during the process.
Identify Key Information and Requirements
The first step in solving any problem is to identify all the important information provided. This includes given values, unknowns, and the conditions set by the problem. Read the question carefully, underline the key points, and make sure you fully understand what is being asked before moving forward.
Apply Relevant Concepts and Techniques
Once you have a clear understanding of the question, think about the concepts and formulas that are relevant to solving the problem. These might include rules about relationships between shapes, properties of numbers, or methods for handling specific types of problems. Apply these techniques step-by-step, ensuring that each calculation or logical deduction follows from the previous one.
By working through the problem systematically and checking your work at each stage, you will ensure accuracy and build confidence as you move toward the solution.
Common Mistakes to Avoid on the Test
When taking a challenging mathematical assessment, even the smallest mistake can affect your overall performance. Many common errors occur due to rushing, misreading the problem, or overlooking important details. Being aware of these pitfalls and learning how to avoid them can significantly improve your chances of success.
Rushing Through Questions
One of the most frequent mistakes is rushing through questions. While time management is important, hurrying can lead to careless errors. Always allocate enough time to carefully read each question and work through the solution methodically. Double-check your work before moving on to the next question.
Misinterpreting the Question
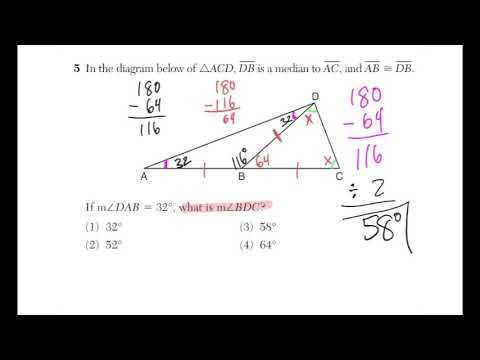
Another common mistake is misinterpreting the question. Many problems contain subtle details or hidden information that can change the way you approach the solution. Take a moment to carefully analyze the wording and underline important terms to ensure you’re solving for the right variables and using the correct methods.
By avoiding these mistakes, you can approach each problem with confidence and precision, ultimately leading to better performance on the test.
Tips for Mastering Geometry Theorems
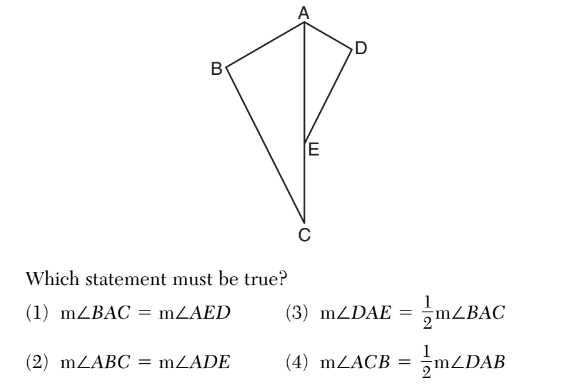
Mastering mathematical theorems requires more than just memorizing formulas–it involves understanding the logic behind each principle and how they connect to one another. A strong grasp of these fundamental concepts is crucial for solving complex problems and proving relationships between different elements in geometric figures. Here are some strategies to help you become proficient in working with theorems.
Understand the reasoning: Rather than focusing solely on rote memorization, focus on understanding why a theorem works. Knowing the reasoning behind a theorem helps you apply it correctly and recognize when and where it can be used. This deeper comprehension will also help you recall theorems more easily during an assessment.
Practice with real-world examples: Apply theorems to practical problems to reinforce your understanding. Working through a variety of example problems will allow you to see how each theorem fits into larger concepts and how they can be used in different contexts. The more you practice, the more intuitive the application of these principles becomes.
Break down complex proofs: When working with proofs, break them down into smaller, manageable steps. Carefully review the given information, and logically connect each step. Writing out proofs clearly and methodically will help you stay organized and avoid making mistakes under pressure.
With regular practice and a focused approach, mastering these key concepts will improve both your understanding and performance on more advanced problems.
Analyzing the Types of Questions in Geometry

Understanding the different types of questions is essential for effective preparation. Mathematical assessments often include a variety of question formats, each designed to test specific skills and knowledge areas. By recognizing these formats, you can tailor your approach to solve problems more efficiently and increase your chances of success.
Multiple-Choice Questions
Multiple-choice questions are typically designed to assess your understanding of fundamental principles and your ability to recognize correct solutions quickly. These questions often include a variety of options, with only one correct answer. It’s important to read each choice carefully and eliminate clearly incorrect options to increase your chances of selecting the right one.
Constructed-Response Problems
Constructed-response questions require more detailed solutions and a deeper understanding of the concepts. These questions test your ability to apply mathematical principles and solve problems step-by-step. In these cases, it is essential to show all of your work, as partial credit may be awarded for the correct process, even if the final answer is incorrect.
By familiarizing yourself with these different question types and practicing the best approaches for each, you will improve your problem-solving efficiency and accuracy during the test.
Time Management Strategies for the Exam
Effective time management is one of the most important skills to develop when preparing for and taking a challenging assessment. Knowing how to allocate your time wisely ensures that you can work through all questions efficiently, without rushing or leaving any unfinished. Proper planning allows you to balance speed with accuracy and complete the test confidently.
Prioritize Easy Questions First
One key strategy is to start with the questions you find easiest. Quickly solve these to build momentum and secure points early on. This approach helps you avoid spending too much time on difficult problems at the beginning and ensures you have enough time for more challenging ones later in the test.
Set Time Limits for Each Section
To manage your time effectively, set a rough time limit for each section or question type. For example, if you know a certain set of questions requires more calculations, give yourself a little extra time for those. Keep track of time throughout the test to ensure you’re progressing at a steady pace. If you’re stuck on a difficult problem, it’s often best to move on and return to it later, rather than wasting time on a single question.
By implementing these strategies, you can maximize your efficiency and ensure that you have sufficient time to review your work before submitting your test.
Essential Geometry Formulas to Know
Understanding key formulas is fundamental to solving problems efficiently. These formulas provide the foundation for solving a wide range of questions, from basic calculations to more complex proofs. Having them committed to memory and knowing when to apply them will significantly improve your performance on mathematical assessments.
Basic Area and Perimeter Formulas
Here are some of the most commonly used formulas in geometry that are essential for calculating areas and perimeters of various shapes:
- Area of a Square: A = s² (where s is the length of a side)
- Area of a Rectangle: A = l × w (where l is length and w is width)
- Perimeter of a Square: P = 4s
- Perimeter of a Rectangle: P = 2(l + w)
- Area of a Circle: A = πr² (where r is the radius)
- Circumference of a Circle: C = 2πr
Important Volume Formulas

For three-dimensional shapes, knowing how to calculate volume is equally important:
- Volume of a Cube: V = s³
- Volume of a Rectangular Prism: V = l × w × h
- Volume of a Cylinder: V = πr²h (where r is the radius and h is the height)
Having these essential formulas at your fingertips will help you solve problems more quickly and accurately, allowing you to tackle even the most complex questions with confidence.
How to Interpret Word Problems in Mathematics

Word problems often require a careful approach to translate verbal descriptions into mathematical expressions. Understanding the key information and identifying what is being asked are crucial steps in solving these problems effectively. By breaking down the text and identifying the relevant data, you can systematically solve the problem using the appropriate formulas or methods.
Here’s a step-by-step guide to interpreting word problems:
| Step | Action |
|---|---|
| 1 | Read the Problem Carefully: Pay attention to all details, such as measurements, relationships, and conditions. Underline key information as you go. |
| 2 | Identify What is Being Asked: Look for clues in the question that indicate what you need to find. This could be an area, perimeter, volume, or an unknown value. |
| 3 | Choose the Right Approach: Decide which mathematical operations or formulas are needed based on the type of problem (e.g., distance, area, angles). |
| 4 | Draw a Diagram: Visualizing the problem can help clarify relationships between elements. Label the diagram with all known values. |
| 5 | Set Up an Equation: Translate the given information into a mathematical equation based on the relationships you identified. |
| 6 | Solve the Equation: Perform the necessary calculations to find the solution, making sure to check each step for accuracy. |
| 7 | Check Your Answer: Verify that the answer makes sense in the context of the problem and that all units are correct. |
By following these steps, you can improve your ability to understand and solve word problems in mathematics with greater accuracy and confidence.
What to Expect on the Assessment
Preparing for a formal assessment in mathematics requires an understanding of the structure and content of the test. Knowing what topics will be covered and the types of questions you may face can help alleviate anxiety and guide your study efforts. This section provides an overview of what to expect, from the format of the test to the kinds of problems you will encounter.
The assessment typically consists of multiple sections designed to test a variety of skills, ranging from basic calculations to more complex problem-solving and reasoning. Here is a breakdown of the components:
| Section | Content | Type of Questions |
|---|---|---|
| Multiple Choice | Questions on fundamental concepts and definitions | Four options, only one correct answer |
| Short Answer | Problem-solving questions requiring brief responses | Numerical answers or short explanations |
| Constructed Response | More complex problems that require detailed step-by-step solutions | Written explanation and calculations |
| Proofs | Logical reasoning and demonstrations of geometric principles | Written proofs using established theorems |
Understanding the structure of the test will help you focus your preparation on the areas that are most likely to be tested. Focus on mastering the foundational concepts, practicing problem-solving techniques, and refining your ability to reason logically through complex questions.
Study Resources for Preparation
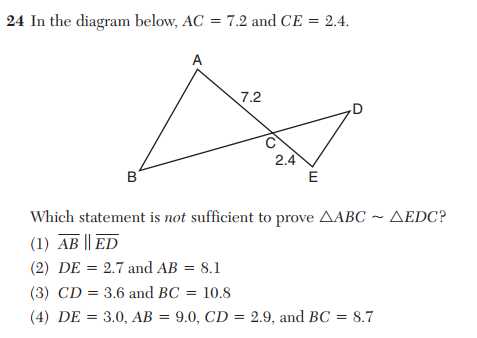
Effective preparation requires access to the right materials and tools that can reinforce understanding and help improve problem-solving skills. Whether you are looking for practice questions, video tutorials, or textbooks, having a variety of study resources can make a significant difference in mastering the concepts. This section highlights some key resources that can help guide your study sessions and boost your confidence before the test.
One of the most beneficial study tools is a comprehensive review book. These books often provide summaries of key concepts, practice problems, and test-taking strategies. Additionally, online resources such as educational websites and video platforms offer interactive lessons that can explain complex ideas in simple terms. You can also use forums and study groups to discuss difficult concepts with peers.
Here are some recommended types of study resources:
- Textbooks and Study Guides: Detailed explanations and example problems to reinforce core concepts.
- Online Practice Tests: Simulate test conditions and gauge your readiness by taking full-length practice tests.
- Video Tutorials: Step-by-step lessons that explain difficult concepts visually and in-depth.
- Interactive Websites: Websites with quizzes, games, and practice problems to help you improve in specific areas.
- Flashcards: Useful for memorizing key formulas and theorems quickly and effectively.
By using a combination of these resources, you can build a solid understanding of the material, identify areas that need further attention, and feel well-prepared for the assessment.
Best Practices for Solving Proofs

Solving mathematical proofs can be a challenging yet rewarding task that requires logical thinking, patience, and a clear understanding of underlying principles. Whether you are proving congruence, similarity, or other geometric properties, the ability to break down the problem into smaller, manageable steps is crucial. In this section, we will discuss some best practices that can help streamline the process and improve your problem-solving skills.
One of the first steps in tackling a proof is to carefully read and understand the given information and what needs to be proven. Identifying the knowns and the unknowns can help you form a strategy. It’s also important to recognize which geometric properties or theorems apply to the situation at hand.
Here are some effective techniques to keep in mind when solving proofs:
- Identify Given Information: Carefully note what is provided and highlight important relationships such as angles, lengths, and parallel lines.
- Use Definitions and Theorems: Apply relevant definitions and theorems to make logical connections between the given elements and what needs to be proven.
- Work Step-by-Step: Avoid skipping steps. Each logical step should be clearly explained, and every statement should be backed up by a reason, such as a definition, postulate, or theorem.
- Look for Patterns: Often, proofs follow common patterns or structures. Familiarize yourself with the most frequently used types of proofs, such as two-column proofs, paragraph proofs, or flowchart proofs.
- Draw Diagrams: Visualizing the problem can help clarify relationships between elements and make the reasoning process easier to follow.
- Work Backwards: In some cases, it may be helpful to start with what you need to prove and work backwards to the given information. This can help you identify key steps more efficiently.
By adhering to these best practices, you’ll not only improve your efficiency in solving proofs but also gain a deeper understanding of the logical structure that governs mathematical reasoning. Remember, practice is key to becoming proficient in solving complex geometric proofs.
Reviewing Key Concepts Before the Test
Before any important assessment, it’s essential to revisit the core ideas and concepts that will be tested. This process helps reinforce your understanding and ensures you’re well-prepared to tackle various types of questions. Whether you’re focusing on shapes, measurements, or transformations, reviewing these concepts systematically can help you confidently approach the test.
In this section, we’ll focus on the most important topics that should be reviewed before the assessment. A clear grasp of these principles will aid in solving problems more efficiently and accurately.
Essential Topics to Revisit
- Properties of Shapes: Understanding the key properties of different shapes is fundamental. Pay attention to the relationships between sides, angles, and symmetry. For example, remember that the sum of interior angles in a triangle is always 180 degrees, or the fact that squares are a special type of rectangle.
- Measurement and Formulas: Be sure to memorize key formulas for area, volume, and perimeter. These are critical for solving problems related to circles, polygons, and three-dimensional objects.
- Angle Relationships: Master concepts such as complementary, supplementary, and vertical angles, and be able to apply them when working with parallel lines and transversals.
- Coordinate Geometry: Understand the relationship between coordinates and geometric figures. Review the distance formula, midpoint formula, and the equation of a line, as these are commonly tested concepts.
- Transformations: Familiarize yourself with the different types of transformations–translation, rotation, reflection, and dilation–and how they affect shapes on the coordinate plane.
Strategies for Effective Review
- Practice Problems: The best way to reinforce concepts is through practice. Solve a variety of problems related to each topic to ensure you’re comfortable with applying what you’ve learned.
- Focus on Weak Areas: Identify any areas where you feel less confident and allocate more time to reviewing those topics. Focused practice can turn weaknesses into strengths.
- Group Study: If possible, study with a group to discuss complex concepts and solve problems together. Explaining ideas to others can reinforce your understanding.
- Use Visual Aids: Diagrams, charts, and geometric sketches are invaluable when revisiting concepts. Visualizing shapes and their properties can improve recall during the test.
By reviewing these fundamental concepts thoroughly, you’ll be well-equipped to perform at your best. Consistent practice and focusing on key topics will ensure you feel confident and ready when it’s time to take the test.
How to Check Your Responses on the Test
When taking a test, it’s important to ensure that the answers you’ve provided are correct and reflect your understanding of the material. Having a strategy for reviewing your work can help you catch mistakes and improve the accuracy of your responses. Properly checking your solutions can make the difference between a good score and a great one.
In this section, we will cover some effective techniques for reviewing your answers, allowing you to identify any potential errors and correct them before time runs out.
Steps for Efficient Answer Review
- Double-Check Your Calculations: For every numerical problem, quickly go over your calculations to ensure there are no arithmetic errors. Rewriting your steps can help you spot any mistakes you may have overlooked initially.
- Read the Question Again: Often, test-takers can misinterpret questions under time pressure. Re-read each question to ensure that you understood it correctly before finalizing your answers.
- Look for Patterns: If you notice that your answers seem inconsistent (e.g., contradicting each other), go back and check for errors in your logic or calculations that could have led to incorrect conclusions.
- Use Process of Elimination: For multiple-choice questions, eliminate any clearly incorrect choices first. This strategy increases your chances of selecting the right answer and allows for a more efficient review process.
Common Pitfalls to Avoid
- Rushing the Review: Don’t skip the review process because you’re running out of time. Even a quick check can help you catch critical mistakes. Prioritize accuracy over speed.
- Ignoring Units: Ensure that all your answers are in the correct units as required by the question. Missing units can cost you points even if the numerical part of your answer is correct.
- Overlooking Details: Be mindful of small details in the problem, such as specific instructions, conditions, or constraints that might affect your answer. These can often be the key to solving a question correctly.
By following these steps and avoiding common mistakes, you can improve your chances of achieving a high score. Taking the time to review your responses thoroughly is a key part of the testing process and will help ensure that your hard work is reflected in your results.