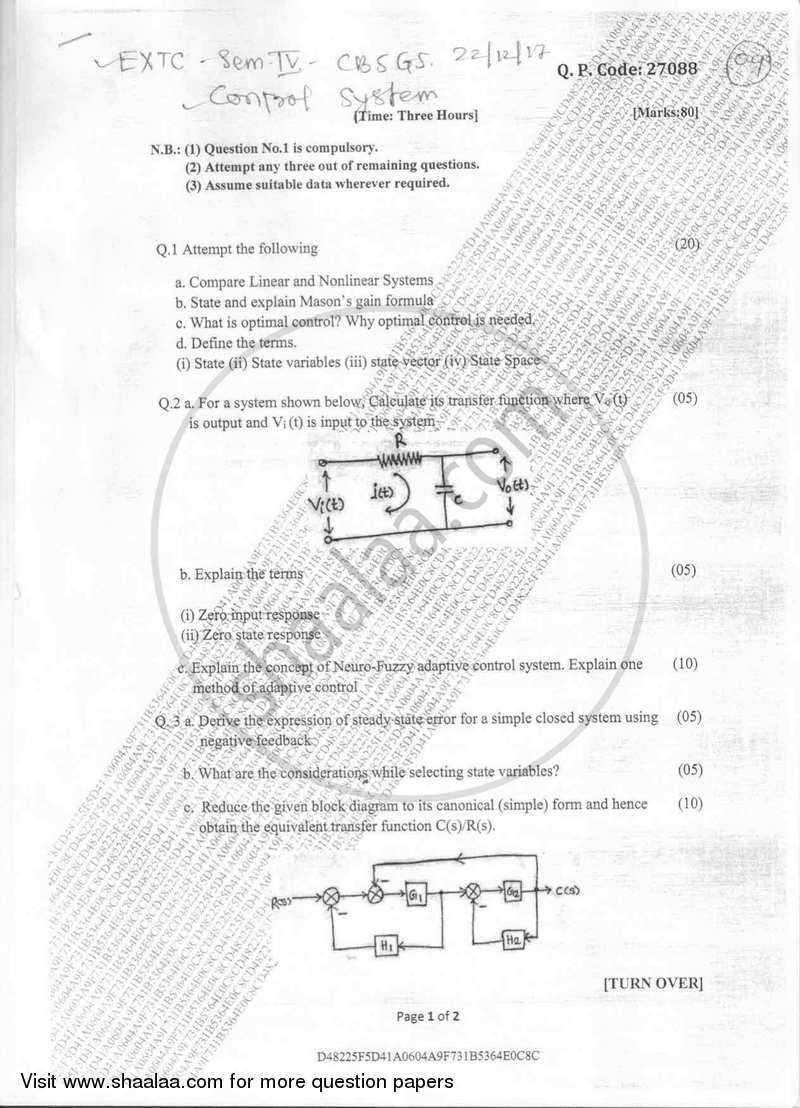
Understanding the core principles and techniques in this field is essential for achieving success in academic evaluations. Whether you are preparing for an upcoming assessment or seeking to reinforce your knowledge, mastering these topics will help you approach the material with confidence and clarity.
In this section, we will explore common challenges students face when tackling theoretical concepts, as well as practical strategies to solve complex problems. A well-rounded preparation involves both grasping the theoretical foundations and developing a methodical approach to troubleshooting and calculations.
With clear explanations, structured examples, and expert tips, this guide aims to provide a comprehensive resource for anyone looking to strengthen their understanding and improve their performance. By focusing on key ideas and applying effective study methods, you can approach your next evaluation with the confidence needed to succeed.
Control Systems Exam Questions and Answers
Preparing for an assessment in this field requires a strong understanding of both theoretical concepts and practical problem-solving techniques. To succeed, it’s crucial to be familiar with the types of challenges that typically arise and how to approach them systematically. This section provides insights into the most commonly encountered topics and how to tackle them efficiently.
Below is a collection of critical areas to focus on, along with suggestions for how to approach similar tasks in an academic setting:
- Understanding the behavior of dynamic models and analyzing their response to different inputs.
- Mastering the use of mathematical tools like Laplace transforms and transfer functions to simplify complex calculations.
- Exploring the concept of stability and learning how to assess it through various criteria.
- Applying feedback principles to design and evaluate systems for real-world applications.
- Identifying time-domain and frequency-domain characteristics and using them to draw conclusions about system performance.
These topics represent a broad scope of material that may appear in assessments. To help reinforce your preparation, here are a few tips for practicing:
- Work through sample problems to get familiar with common problem types and their solutions.
- Study key formulas and principles, ensuring that you understand how to apply them in various contexts.
- Review detailed examples that show step-by-step solutions to complex problems.
- Test your knowledge by solving mock problems under timed conditions to improve speed and accuracy.
By focusing on these areas and practicing regularly, you can enhance your ability to solve problems efficiently and confidently during any evaluation. The more familiar you become with these topics, the easier it will be to apply the necessary techniques to achieve optimal results.
Overview of Control Systems in Exams
Assessments in this field typically focus on evaluating your understanding of both fundamental concepts and practical applications. These evaluations often test your ability to analyze various models, design solutions, and solve complex problems using theoretical knowledge and mathematical techniques. The structure of such evaluations may vary, but they commonly include both conceptual and problem-solving components.
In general, the topics covered can range from basic principles such as feedback loops and stability analysis, to more advanced concepts involving transfer functions, system behavior, and time-frequency domain analysis. Being well-prepared means not only mastering the theoretical material but also practicing how to apply it effectively in different scenarios.
Typically, you will encounter problems that require a deep understanding of how systems respond to external factors and how to model these behaviors. Examining the interplay between various components and their overall performance is a crucial skill that is frequently tested in such assessments.
Key Topics in Control Systems Theory
Mastering the foundational concepts in this field is essential for understanding how various components interact and influence overall performance. Several key areas form the core of the theoretical framework, and a strong grasp of these concepts is crucial for solving problems effectively. From fundamental principles to more advanced techniques, each topic offers unique insights that contribute to a well-rounded knowledge base.
Among the most important subjects are feedback mechanisms, stability criteria, and dynamic response analysis. A deep understanding of these areas enables you to assess system behavior and predict how adjustments will impact performance. Additionally, concepts such as transfer functions, block diagrams, and frequency response analysis are integral to both theoretical study and practical applications.
Another critical area is the study of modeling techniques, which allow for the representation of physical phenomena in mathematical terms. This helps to predict how changes in one part of a model will affect the rest of the system. By delving into these key topics, you’ll develop the skills needed to approach complex challenges with confidence and accuracy.
Common Control Systems Exam Formats

In evaluations of this field, the structure of the assessment plays a significant role in how concepts are tested. Typically, these assessments combine multiple types of questions, each designed to evaluate different aspects of understanding and application. The format can range from theoretical problem-solving to more practical, application-based challenges, requiring a diverse set of skills.
Theoretical Problems
One common format is the inclusion of theoretical problems that focus on the underlying principles and laws. These may require you to demonstrate your understanding of specific concepts, such as stability, feedback loops, and dynamic response. The goal is to assess your ability to explain and reason through complex topics logically and succinctly.
Practical Application Challenges
Another widely used format involves practical challenges, where you must apply theoretical knowledge to solve real-world problems. These questions often include calculations, system modeling, or the design of components. The emphasis here is on your ability to apply learned techniques in a problem-solving context, testing both accuracy and creativity in your approach.
In both formats, clarity and precision are crucial. Effective preparation should focus on both conceptual knowledge and the ability to apply it practically, ensuring you are well-equipped for the diverse types of challenges you may encounter.
Important Concepts to Master for Success
Achieving success in this field requires a deep understanding of several fundamental principles. Mastering these core ideas is essential for not only passing assessments but also for effectively solving practical challenges. A strong foundation in the following concepts will enable you to navigate complex problems with confidence and precision.
Feedback Mechanisms

Feedback is a crucial concept that determines how systems adjust their behavior based on input or changes in the environment. Mastering feedback loops–both positive and negative–is essential for understanding stability and performance. This concept is frequently tested, as it plays a central role in regulating system behavior and maintaining desired outputs.
Stability Analysis

Understanding how to analyze the stability of a system is critical. This includes knowing how to assess whether a system will remain stable under varying conditions or if it will become unstable. Techniques such as root locus, Nyquist plots, and Bode plots are vital tools in this area, helping you predict system performance and identify potential issues before they arise.
By focusing on these concepts and developing a solid understanding of their applications, you will be well-prepared for any challenge in this field. Consistent practice and deep engagement with these ideas are the keys to achieving success.
Commonly Asked Questions on Stability
Stability is one of the most crucial aspects in this field, as it directly affects the reliability and performance of systems. Understanding how to evaluate and ensure stability under varying conditions is essential for success. In assessments, it’s common to encounter problems that test your ability to identify and analyze stable and unstable behaviors, often requiring the use of specific techniques and criteria.
How Do You Determine Stability in a Model?
One of the fundamental questions in this area is how to determine if a model or system will remain stable over time. Key techniques such as the Routh-Hurwitz criterion, Nyquist criterion, or the use of root locus plots are often employed to assess stability. Understanding how to apply these methods is essential for recognizing unstable behaviors and predicting system responses.
What Role Do Feedback Loops Play in Stability?
Another common question revolves around the influence of feedback loops on stability. Negative feedback typically enhances stability by reducing the impact of disturbances, while positive feedback can lead to instability. Analyzing how different types of feedback affect the system is crucial for designing stable and reliable configurations.
Mastering these concepts and techniques will help you confidently approach stability-related problems, enabling you to determine system behaviors and suggest necessary adjustments to maintain stability.
Understanding Transfer Functions for Exams
In evaluations of this field, understanding how to represent and manipulate transfer functions is crucial. These mathematical models allow for a simplified representation of complex behaviors, making it easier to analyze system responses to various inputs. Mastery of transfer functions not only aids in solving theoretical problems but is also a key skill when working with real-world models and simulations.
What Are Transfer Functions?

A transfer function represents the relationship between the input and output of a system in the frequency domain. It is a powerful tool used to understand how a system behaves when subjected to different stimuli. By converting differential equations into algebraic equations, the transfer function simplifies the analysis of dynamic systems.
Key Steps to Analyze Transfer Functions
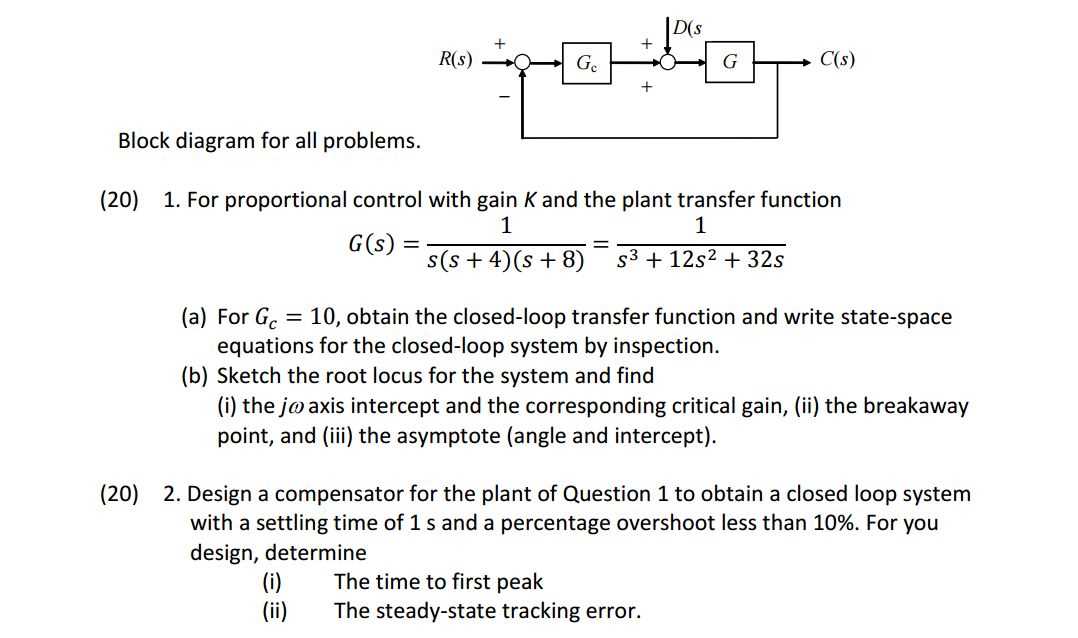
To master the use of transfer functions, it’s essential to follow a systematic approach:
- Identify the components: Understand the elements of the system, including inputs, outputs, and internal parameters.
- Derive the transfer function: Use mathematical techniques, such as Laplace transforms, to obtain the transfer function from the system’s differential equation.
- Analyze poles and zeros: Evaluate the stability and response characteristics by examining the poles and zeros of the transfer function.
- Apply to real-world scenarios: Use the transfer function to predict system behavior under various conditions and adjust parameters as needed.
By focusing on these key steps, you can efficiently analyze transfer functions and apply your knowledge to a wide range of problems. This skill is foundational for both theoretical assessments and practical applications in engineering and design tasks.
Feedback Systems and Their Role
Feedback mechanisms play a vital role in shaping the behavior of dynamic models. These mechanisms are designed to regulate and control outputs by adjusting inputs based on system performance. By understanding how feedback influences stability and response time, you can optimize system behavior to meet desired specifications. The study of these mechanisms is crucial for both theoretical analysis and practical applications in various fields.
Types of Feedback
There are two primary types of feedback mechanisms: positive and negative. Both play distinct roles in determining how a system reacts to changes and disturbances. Understanding their differences is essential for controlling system behavior effectively.
| Type of Feedback | Description | Impact on System |
|---|---|---|
| Negative Feedback | Reduces the effect of external disturbances and helps stabilize the system. | Improves accuracy and stability. |
| Positive Feedback | Amplifies the effect of changes, often leading to instability. | Can lead to runaway behavior if not properly controlled. |
Role in System Behavior
The role of feedback is pivotal in ensuring that a model behaves as expected under various conditions. Negative feedback is commonly used in control applications to maintain stability and minimize errors, while positive feedback can sometimes be used for amplification in systems like oscillators. A deep understanding of how these feedback mechanisms work helps predict and manage system behaviors more effectively, ensuring desired performance levels are achieved.
Frequently Tested Control System Models

In assessments related to this field, certain models are frequently used to test understanding and problem-solving skills. These models help to represent real-world systems and their dynamic behavior in a simplified mathematical form. By mastering these common models, you can develop a more intuitive understanding of how different components interact and respond to changes over time.
First-Order Models
First-order models are among the simplest and most frequently tested. These models describe systems that have one energy storage element, such as a capacitor or an inductor, and exhibit exponential response characteristics. They are often used to test basic concepts like time constants and transient behavior.
For example, a simple first-order system can be represented by the equation:
G(s) = 1 / (τs + 1)
Where τ is the time constant, and s is the Laplace transform variable. The system’s response can be analyzed to understand how quickly it reaches steady-state behavior.
Second-Order Models
Second-order models are also commonly encountered, particularly when dealing with oscillatory behavior. These models involve two energy storage elements and are useful for understanding more complex behaviors such as overshoot, oscillation, and damping. The standard form for a second-order system is:
G(s) = ω_n² / (s² + 2ζω_n s + ω_n²)
Where ω_n is the natural frequency, and ζ is the damping ratio. The damping ratio is particularly important as it determines whether the system will be underdamped, critically damped, or overdamped.
By mastering these models, you can gain a deeper understanding of how different systems behave and how their performance can be optimized. These models serve as the foundation for more complex systems and are often used to assess both theoretical knowledge and practical problem-solving skills.
Exam Strategies for Control Systems
Successfully tackling assessments in this field requires more than just understanding theory; it involves applying strategies that allow you to efficiently navigate through complex problems. By organizing your approach, managing time effectively, and knowing how to break down problems, you can increase your chances of success. Here are some key techniques that can help you perform your best during evaluations.
Preparation Tips
Before the assessment, thorough preparation is essential. Understanding the core principles and familiarizing yourself with common models can provide a solid foundation. Here are some strategies to maximize your study time:
- Practice with past problems: Solve previous assessments to identify patterns and familiarize yourself with commonly tested topics.
- Focus on key concepts: Make sure you are comfortable with the fundamental principles, such as response analysis, stability, and transfer functions.
- Use study groups: Discussing problems with peers can help you see different approaches and clarify any uncertainties.
- Create summary notes: Write down essential formulas and methods for quick reference during study sessions.
During the Assessment
During the actual evaluation, your strategy should focus on efficiency and clarity. Here’s how you can approach the test:
- Read carefully: Take time to read each problem thoroughly to ensure you understand what is being asked before jumping to the solution.
- Plan your time: Allocate a specific amount of time to each section based on its difficulty and the marks it carries. Avoid spending too much time on a single question.
- Start with familiar questions: Begin with problems you are confident about to build momentum and ensure you earn easy marks first.
- Show your work: Write out all calculations and reasoning clearly. Even if you make a mistake, showing your process can earn partial credit.
- Review your answers: If time permits, review your responses to check for any mistakes or overlooked details.
By applying these strategies, you can approach the assessment with confidence, ensuring that you have a well-rounded approach to solving problems effectively and efficiently. Preparation and smart time management are essential components of success in any assessment.
Real-World Applications in Control Systems
The principles of regulation and feedback are not just theoretical concepts; they are applied across numerous industries to manage complex processes and ensure optimal performance. From manufacturing plants to space exploration, the ability to adjust and stabilize dynamic systems is essential. Understanding how these principles are used in practical applications provides insight into their significance and versatility.
Industrial Automation
One of the most common areas where regulation techniques are applied is in industrial automation. Factories and production lines rely heavily on automated machinery to ensure consistency and precision in manufacturing. These systems are designed to adjust operational parameters, such as speed, temperature, or pressure, to maintain desired outputs and minimize errors.
For example, in automotive manufacturing, robotic arms are programmed to perform tasks like welding and assembly with high accuracy. The systems responsible for controlling these robots constantly monitor the environment and adjust movements to ensure that each part is correctly placed and fastened.
Aerospace Engineering
In aerospace engineering, regulation is crucial for ensuring the stability and performance of aircraft and spacecraft. Automatic flight control systems, for instance, use feedback loops to make real-time adjustments to control surfaces, ensuring smooth and stable flight. Similarly, spacecraft use guidance systems to maintain their trajectory and orientation during space missions.
These advanced technologies rely on precise mathematical models to predict and correct any deviations from the planned path, allowing for safe travel in the challenging environment of space. The success of missions, such as satellite launches or interplanetary travel, depends on the efficiency of these feedback systems in maintaining optimal conditions throughout the journey.
Complexity in Control Systems Questions
The difficulty level of problems in this field varies widely, ranging from basic calculations to highly complex theoretical challenges. The primary challenge comes from the need to apply a combination of mathematical concepts, practical knowledge, and logical reasoning to solve real-world scenarios. Understanding the complexity of these problems is key to managing them effectively during assessments or real-life applications.
Many problems require a deep understanding of dynamic behavior, feedback loops, and time-domain or frequency-domain analysis. Solving these challenges involves recognizing patterns, simplifying models, and applying the right techniques to obtain accurate solutions. Often, questions will involve multi-step processes, where each phase builds upon the previous one, requiring students or practitioners to think critically and adjust their approach as new information is provided.
In more advanced cases, the challenge can also stem from dealing with uncertainty, non-linearity, and disturbances, which introduce additional layers of complexity. Problems that involve designing or tuning specific solutions add another dimension of difficulty, requiring creativity in the application of learned principles. The ability to break down these complex problems into manageable steps and make informed assumptions when necessary is crucial to finding correct and efficient solutions.
Time-Domain vs Frequency-Domain Questions
Problems in this field can often be classified into two main approaches: those that focus on analyzing system behavior over time, and those that consider the system’s response in terms of frequency. Both approaches provide different insights into how a system behaves, and understanding when to use each method is essential for solving real-world challenges effectively.
Time-Domain Analysis
Time-domain problems typically involve examining how a system reacts over a period, analyzing parameters such as rise time, settling time, overshoot, and steady-state error. These aspects are particularly useful for understanding the dynamic response of systems to different inputs or disturbances. Time-domain analysis allows engineers to assess system stability and performance directly, often through step responses or impulse tests.
Such problems usually require solving differential equations or using numerical methods to simulate the system’s behavior over time. Mastery of these techniques is crucial for those dealing with systems that need to perform accurately and reliably within specific time frames.
Frequency-Domain Analysis
In contrast, frequency-domain questions focus on the system’s behavior in terms of sinusoidal inputs at varying frequencies. By transforming the system’s time-domain representation into the frequency domain (often using tools like Laplace or Fourier transforms), one can gain insights into stability margins, resonance, and bandwidth. These characteristics are critical for understanding how a system will behave when subjected to varying frequencies or periodic inputs.
Frequency-domain analysis is especially helpful when designing systems with specific frequency requirements, such as communication systems or signal processing. By analyzing the system’s transfer function or Bode plots, one can easily assess system performance across a range of frequencies, providing a clearer picture of how the system will behave under different conditions.
Practical Tips for Control System Studies
Mastering complex topics in this field requires both theoretical knowledge and hands-on practice. Developing a deep understanding involves combining textbooks with practical applications, so students or professionals can visualize how abstract concepts work in real-world scenarios. Incorporating the right study strategies can make a significant difference in mastering the material and applying it effectively.
Organizing Study Sessions
Breaking down the material into manageable sections is crucial for keeping track of progress. Focus on understanding one concept thoroughly before moving to the next, rather than trying to memorize large amounts of information at once. Review key principles and reinforce them by solving related problems regularly.
It’s important to actively engage with the content by solving different types of exercises. This reinforces learning and helps to build a practical understanding. Additionally, seeking out problems that challenge your existing knowledge can help identify areas that need more attention.
Utilizing Available Resources

There is a wide range of resources available, from textbooks to online tutorials, forums, and simulation tools. Using these resources effectively can provide various perspectives and deepen understanding. Many simulation software tools allow you to experiment with different models, providing visual feedback and aiding in the learning process.
Working with peers or instructors can also provide new insights, as discussing different methods and approaches helps reinforce your understanding. Don’t hesitate to ask for clarification when you encounter difficult concepts–collaboration can significantly improve retention and comprehension.
| Tip | Details |
|---|---|
| Divide Study Material | Break topics into smaller parts and focus on mastering each section before moving on. |
| Practice Regularly | Regularly solve problems to reinforce concepts and improve problem-solving skills. |
| Use Simulation Tools | Simulate real-world problems using software tools to better understand the theory. |
| Collaborate with Others | Discuss difficult concepts with peers or mentors to gain new perspectives. |
Reviewing Key Control System Formulas
In any technical discipline, formulas serve as fundamental tools for solving problems and analyzing various processes. For those studying the intricacies of dynamic models, understanding and applying these mathematical expressions is crucial. A solid grasp of essential equations allows for efficient problem-solving and deeper insight into the functioning of complex mechanisms.
Fundamental Equations to Master
Many important calculations rely on a set of basic formulas that describe system behavior, stability, and response to inputs. These key formulas are not just theoretical–they are widely used in practical applications to design, test, and optimize systems in various industries.
- Transfer Function: This equation relates the output of a system to its input in the frequency domain, providing a clear representation of the system’s behavior.
- Stability Criteria: Mathematical criteria, such as the Routh-Hurwitz criterion, help determine the stability of a system, ensuring that it behaves predictably.
- Time Domain Response: Equations like the step response and impulse response characterize how a system reacts over time to different inputs, essential for analyzing performance.
- Frequency Domain Analysis: Formulas like Bode plots and Nyquist diagrams allow for understanding how a system responds across a range of frequencies, offering insight into stability and performance.
Application of Formulas in Problem Solving
To efficiently apply these formulas, it’s important to understand not only their individual components but also how they interact in specific contexts. Whether it’s finding the transfer function of a given model or analyzing the frequency response, consistent practice with these equations helps reinforce their utility.
- Step-by-Step Problem Solving: Break down the problem into manageable parts and identify which equations are applicable. Solve for unknowns systematically.
- Modeling and Simulation: Use simulation tools to verify theoretical solutions and see how formulas perform in real-world scenarios.
- Regular Review: Repetition is key–frequent review of these formulas ensures fluency in using them when required.
How to Tackle Difficult Exam Problems
When faced with challenging problems during an assessment, staying calm and methodical is key. Difficult tasks often test your ability to think critically, break down complex concepts, and apply learned principles effectively. The goal is not just to find an answer, but to understand the process and approach each problem with clarity and confidence.
Step-by-Step Approach
Start by carefully reading the problem to ensure you understand all the given information. Sometimes, the complexity arises from misinterpreting the problem itself. Once you have a clear grasp, break it down into smaller, more manageable steps.
- Identify the core challenge: What is the problem asking? What do you need to find?
- List known variables: Write down all provided data or equations that could help solve the issue.
- Look for patterns: Often, difficult problems are variations of simpler ones. Identify similarities to make the solution easier.
- Work backwards: If stuck, try working backwards from the desired result to see if you can deduce the necessary steps.
Handling Complex Formulas
When a problem involves complex equations or models, it’s important to take a systematic approach. Do not rush to apply formulas without understanding the context in which they are used. Focus on understanding the underlying concepts before jumping into calculations.
- Focus on units: Make sure the units are consistent throughout your calculations to avoid confusion or errors.
- Use approximation: If the numbers seem too large or complicated, consider using approximations to simplify the process.
- Double-check your work: Before finalizing the answer, quickly review your steps to ensure that no critical steps have been missed.
Self-Assessment and Practice Tests
One of the most effective ways to prepare for challenging assessments is through consistent self-evaluation and targeted practice. Regularly testing your knowledge helps to reinforce key concepts, identify areas of weakness, and build confidence. By simulating real-world tasks, you can gauge your understanding and improve problem-solving skills before facing a formal evaluation.
Benefits of Self-Assessment
Self-assessment allows you to monitor your progress and adjust your study techniques as needed. It also helps in pinpointing specific areas that require further focus. This practice can be as simple as reviewing past materials or attempting exercises that cover a range of topics.
- Track your strengths and weaknesses: Identify topics that come easily to you and those that require more effort.
- Improve time management: Simulating test conditions helps you gauge how much time you need for different sections.
- Enhance retention: By revisiting previously studied material, you solidify your understanding and improve recall.
Practice Tests: Simulating Real Challenges
Taking practice tests is a powerful tool for preparing for complex evaluations. These tests replicate the structure and difficulty of actual tasks, helping you become more familiar with the type of material you will encounter. Consistent practice also improves your ability to manage stress and time effectively.
- Recreate real conditions: Set a timer and work through problems without distractions to simulate actual conditions.
- Analyze mistakes: Review each test thoroughly and understand where you made errors to avoid repeating them.
- Vary difficulty levels: Gradually increase the difficulty of the tasks to challenge yourself and expand your problem-solving skills.
Resources for Further Study in Control Systems
Expanding your understanding of key concepts and refining your skills often requires access to diverse educational materials. Whether you prefer textbooks, online courses, or interactive tools, there are numerous resources available to support deeper exploration. Utilizing these materials can help solidify your grasp of complex topics and offer alternative perspectives to enhance your learning process.
Below are a few valuable resources that can guide you in your continued studies:
- Textbooks and Reference Books: Authoritative texts often provide in-depth coverage of fundamental principles, advanced theories, and real-world applications. Look for books that explain concepts in detail and offer practice problems to help reinforce learning.
- Online Courses: Platforms like Coursera, edX, and Udemy offer courses designed by industry professionals and academic institutions. These courses often include video lectures, quizzes, and hands-on assignments that help you learn at your own pace.
- Academic Journals and Research Papers: Access to recent research can provide insights into cutting-edge advancements and more complex theories. Websites like Google Scholar and JSTOR can help you find peer-reviewed papers that deepen your knowledge.
- Interactive Simulations and Software: Tools like MATLAB and Simulink provide interactive environments to model, simulate, and analyze systems in real-time. These hands-on experiences are invaluable for visualizing how theoretical concepts apply to real-world scenarios.
- Online Forums and Communities: Participating in online forums, such as Stack Exchange or Reddit, allows you to ask questions, share experiences, and collaborate with peers. These communities are great for solving problems and learning from others’ perspectives.
Combining these resources with dedicated study habits and regular practice will enable you to continue improving and mastering the concepts essential for success in your field.