Advanced Business Statistics Exam Questions and Answers

Mastering complex problems related to numerical data analysis is a critical skill for anyone aiming to succeed in academic assessments. Understanding key concepts and practical applications can make a significant difference in how well one tackles difficult topics. This guide offers a comprehensive approach to preparing for challenges that test analytical thinking and problem-solving abilities.

Effective preparation involves not only memorizing formulas but also gaining a deeper understanding of how to apply them in real-world scenarios. The ability to interpret results, recognize patterns, and make informed decisions is essential for success in any subject that deals with numbers and data.

Strategic study techniques can help in navigating through complex problems with ease, ensuring that each section is thoroughly understood. This approach encourages a methodical process, focusing on areas that often appear in assessments while refining techniques that lead to better performance under pressure.

Advanced Business Statistics Exam Questions and Answers

When preparing for tests that assess analytical reasoning and quantitative problem-solving, it is essential to focus on various types of challenges that often appear. These challenges typically involve interpreting data sets, performing calculations, and making sense of patterns within the information provided. Each problem requires a unique approach, whether it is based on probability theory, regression analysis, or other techniques used to extract meaningful insights from numbers.

Familiarity with key formulas and their applications is crucial for success. A clear understanding of how to use these formulas in different contexts will enable one to handle a wide range of problems, from basic to more complex tasks. For example, knowing when and how to apply concepts such as confidence intervals or hypothesis testing can dramatically improve the accuracy of responses during an assessment.

Consistent practice with sample problems and past assessments is one of the most effective ways to prepare. Regular exposure to a variety of scenarios helps to build confidence and ensures that individuals are not caught off guard by unfamiliar problem types. Moreover, focusing on areas that commonly appear in assessments can streamline the study process, making preparation more efficient.

Understanding Key Statistical Concepts for Exams

Grasping core principles in data analysis is essential for success in assessments that challenge your ability to make informed decisions from numerical information. Key concepts such as probability, distribution, and regression are frequently tested, requiring not only knowledge of formulas but also a deep understanding of how they apply to real-world situations. This foundational knowledge serves as the backbone for tackling various types of problems encountered during evaluations.

It is important to familiarize oneself with the different methods of data interpretation. Knowing how to identify trends, calculate central tendency measures, and understand the variability within data sets can significantly impact performance. A solid grasp of these techniques ensures that solutions are not only accurate but also based on sound analytical reasoning.

Beyond basic comprehension, applying these concepts in diverse scenarios is crucial. Practical experience, through practice exercises or sample problems, helps strengthen the ability to select the most appropriate technique for each problem, ultimately leading to more efficient and accurate responses under test conditions.

Common Challenges in Business Statistics Exams

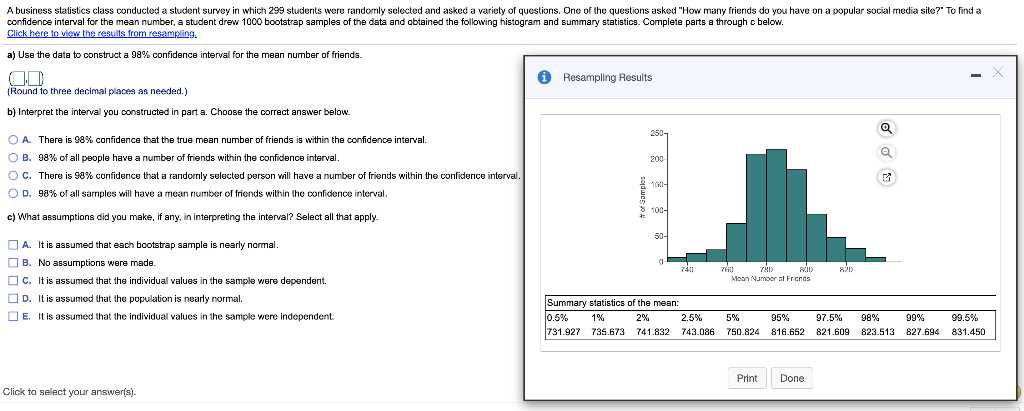
When facing assessments that test knowledge in data analysis and interpretation, many students encounter specific difficulties that can hinder their performance. These challenges often arise from the complex nature of the material, requiring both conceptual understanding and practical application. Mastering these areas is key to successfully navigating through problems that involve numerical analysis, pattern recognition, and decision-making based on data.

Complex Calculations and Formulas

One of the most common obstacles involves the application of complex formulas and calculations. These formulas are essential for solving various types of problems, but their correct use requires familiarity with each component and understanding when to apply them. Mistakes often occur when one formula is incorrectly substituted for another, or when steps in multi-stage problems are skipped.

Data Interpretation and Decision Making

Another challenge arises in interpreting data correctly and making decisions based on it. In many cases, test-takers are required to analyze data sets and determine appropriate actions or conclusions. This may involve identifying trends, calculating averages, or forecasting future values. Misunderstanding the data or drawing incorrect conclusions from it can lead to errors, even if the initial calculations were accurate.

Challenge	Common Mistakes	How to Overcome
Formula Application	Incorrect substitution of formulas	Review key formulas and practice with varied examples
Data Interpretation	Misinterpreting trends or patterns	Focus on understanding data context and practice visual analysis
Time Management	Spending too much time on one problem	Practice solving problems under time constraints

With careful preparation and consistent practice, these challenges can be mitigated, enabling a more confident and effective approach to problem-solving during assessments. Focusing on improving both technical skills and decision-making abilities can lead to more accurate solutions and better exam results.

Preparing for Hypothesis Testing Questions

Hypothesis testing is a critical component of any assessment that focuses on analyzing numerical data and drawing conclusions based on evidence. It involves formulating a claim about a population parameter and using sample data to determine whether there is enough support to accept or reject that claim. A strong understanding of the process, from setting up hypotheses to interpreting p-values, is essential for tackling related problems successfully.

Preparation for these types of tasks requires familiarity with the steps involved in hypothesis testing. The process typically begins with defining the null and alternative hypotheses, followed by choosing the correct test based on the data. Then, calculating the test statistic and determining the corresponding p-value is essential in making an informed decision about the hypothesis. Knowing when to reject or fail to reject the null hypothesis is a key skill that can be developed through practice and repetition.

Additionally, understanding the different types of tests, such as z-tests and t-tests, and when to use them is crucial for accurate results. Each test has specific conditions and assumptions that must be met, and recognizing these details can significantly impact the accuracy of the outcome. By practicing various examples and familiarizing oneself with the logic behind each test, one can confidently approach any hypothesis-related problems in an assessment.

Analyzing Data Interpretation in Statistics

Interpreting data effectively is an essential skill for tackling problems that require extracting meaningful insights from numerical information. The ability to understand and analyze trends, patterns, and relationships within a data set can significantly impact decision-making processes. This section focuses on how to approach data interpretation and the techniques that lead to accurate conclusions.

Key Techniques for Data Interpretation

When faced with data, it’s crucial to use the right methods to draw conclusions. Some of the key techniques include:

• Identifying central tendencies: Recognizing the mean, median, and mode helps provide an overview of data distribution.
• Recognizing data spread: Understanding the range, variance, and standard deviation allows for assessing the variability within the data set.
• Analyzing relationships: Techniques like correlation and regression help to identify connections between variables.

Common Pitfalls to Avoid

While interpreting data, there are several common mistakes that should be avoided to ensure accurate analysis:

1. Overlooking outliers: Extreme values can distort the results and should be carefully considered or excluded where necessary.
2. Misinterpreting correlation: Remember that correlation does not imply causation. It is important to consider other factors that may influence the relationship.
3. Ignoring data context: Always consider the context in which the data was collected to avoid drawing misleading conclusions.

By mastering these techniques and being aware of common pitfalls, one can improve the accuracy of data interpretation, ultimately leading to better conclusions and decision-making.

Essential Probability Questions in Exams

Probability is a fundamental concept that frequently appears in assessments involving quantitative analysis. The ability to calculate the likelihood of different outcomes and understand the principles behind random events is essential for success. Whether dealing with simple or complex scenarios, mastering the key probability concepts can significantly enhance performance in related tasks.

There are several types of problems commonly tested, ranging from basic probability calculations to more complex questions involving conditional probability, combinations, and distributions. These problems require not only a solid understanding of core principles but also the ability to apply them correctly in different contexts.

Problem Type	Description	Key Concept
Basic Probability	Calculating the likelihood of a single event occurring	Understanding of favorable outcomes versus total outcomes
Conditional Probability	Determining the probability of an event given that another has occurred	Bayes’ Theorem
Combinations and Permutations	Calculating the number of ways events can occur in different orders	Factorial rule
Probability Distributions	Understanding distributions such as binomial, normal, and Poisson	Probability mass and density functions

By practicing these types of problems, students can sharpen their probability skills and gain confidence in solving more complex scenarios. A strategic approach to understanding these concepts can help avoid common mistakes and improve accuracy when calculating probabilities during assessments.

Linear Regression and Its Application

Linear regression is a powerful tool used to understand relationships between variables and predict future outcomes based on historical data. This method helps determine how changes in one variable are associated with changes in another. By creating a mathematical model that represents this relationship, one can make informed decisions or predictions about future trends.

There are various scenarios where this technique can be applied, from predicting sales growth to estimating the impact of various factors on product pricing. The simplicity of linear regression makes it a widely used method in both academic and professional settings, providing essential insights into data patterns and trends.

Steps in Applying Linear Regression

The process of applying linear regression involves several key steps:

1. Data Collection: Gather relevant data points that will be used for analysis.
2. Model Fitting: Use the collected data to fit a linear model by calculating the line of best fit.
3. Interpretation: Analyze the relationship between the variables based on the slope and intercept of the line.
4. Prediction: Use the model to predict future values based on new inputs.

Applications of Linear Regression

Linear regression can be used in a variety of fields, including:

• Market Analysis: Estimating the effect of marketing campaigns on sales or customer behavior.
• Finance: Predicting stock prices or determining risk factors based on historical financial data.
• Healthcare: Analyzing the relationship between variables such as age, lifestyle, and health outcomes.
• Manufacturing: Forecasting production rates or quality based on past performance data.

By mastering linear regression, individuals can unlock valuable insights from data and apply them effectively to solve real-world problems, improving decision-making and outcomes in various industries.

Time Series Analysis in Exam Questions

Time series analysis involves studying data points that are collected or recorded at specific time intervals. This method is used to identify trends, patterns, and seasonal effects that evolve over time. When preparing for assessments focused on time-based data, it is essential to understand how to handle such sequences and interpret the underlying patterns accurately.

In these tasks, students are often required to analyze data that tracks changes over time, such as stock prices, weather patterns, or sales figures. The goal is to recognize patterns, forecast future values, and make data-driven predictions. Mastering this skill is crucial for solving problems that involve temporal data trends.

Key concepts involved in time series analysis include:

• Trend Analysis: Identifying long-term movements in the data, such as upward or downward trends.
• Seasonality: Recognizing recurring patterns or fluctuations at regular intervals, often due to seasonal factors.
• Cyclic Patterns: Understanding long-term oscillations that may be caused by economic cycles or other long-duration influences.
• Forecasting: Using past data to predict future values and trends.

Successfully tackling these types of tasks requires familiarity with various techniques and methods for analyzing time-based data. Whether through smoothing techniques or regression models, understanding how to decompose time series data and make accurate forecasts is key to answering these questions effectively.

Sampling Techniques and Their Importance

In any analytical study, selecting the right sample is crucial for obtaining reliable and accurate results. The process of sampling allows researchers to draw conclusions about a larger population by examining a smaller subset. Proper sampling techniques ensure that the sample is representative, minimizing biases and providing insights that can be generalized.

Different methods of selecting samples are used depending on the research objectives, available data, and the desired level of precision. Each technique has its strengths and limitations, and understanding these is key to applying the right approach to a given problem.

Some of the most common sampling methods include:

• Simple Random Sampling: Every individual in the population has an equal chance of being selected. This method is widely used for its simplicity and fairness.
• Systematic Sampling: Individuals are selected at regular intervals from a list. It’s a practical approach when working with large datasets.
• Stratified Sampling: The population is divided into subgroups, and samples are taken from each group to ensure diversity in the sample.
• Cluster Sampling: The population is divided into clusters, and a random selection of clusters is chosen for analysis. This method is effective when populations are geographically spread out.

Choosing the appropriate technique helps improve the quality of the data analysis and ensures that the conclusions drawn are both valid and relevant. A well-chosen sampling method can save time and resources, while a poor one can lead to misleading results and erroneous conclusions.

Understanding Confidence Intervals for Exams

Confidence intervals are a key concept when estimating unknown population parameters based on sample data. They provide a range of values within which the true parameter is likely to lie, offering insight into the precision of the estimate. Mastering this concept is essential for evaluating the reliability of statistical results in various scenarios.

When preparing for assessments involving confidence intervals, it is important to understand how to calculate them and interpret their meaning. A wider interval indicates less precision, while a narrower interval suggests a more precise estimate. Knowing how to choose the appropriate level of confidence and how to apply this concept in different contexts is crucial for tackling related tasks.

Steps to Calculate Confidence Intervals

Here are the main steps to calculate a confidence interval:

1. Identify the sample mean: Calculate the average of the sample data.
2. Determine the standard error: Use the sample standard deviation and the sample size to calculate the standard error.
3. Select the confidence level: Choose a confidence level (e.g., 95%) to reflect how certain you are that the interval contains the true parameter.
4. Calculate the margin of error: Multiply the standard error by the critical value from the relevant statistical distribution.
5. Construct the interval: Add and subtract the margin of error from the sample mean to create the interval.

Interpreting Confidence Intervals

Once the confidence interval is calculated, it’s important to understand its implications:

• 95% Confidence Level: There is a 95% probability that the true population parameter lies within the interval.
• Wider Interval: The interval is less precise and indicates more uncertainty in the estimate.
• Narrower Interval: The interval is more precise, but it may require a larger sample size or lower confidence level.

Understanding confidence intervals enables you to assess the reliability of your estimates and make informed decisions based on sample data. This skill is essential for tackling problems in various analytical contexts.

Key Formulas for Business Statistics Tests

Mastering key mathematical formulas is essential for solving problems that involve data analysis, interpretation, and prediction. These formulas form the foundation for various methods used to analyze and interpret numerical data in an efficient and accurate manner. Knowing when and how to apply these formulas is crucial for achieving success in assessments focused on data-driven tasks.

Below are some of the most commonly used formulas in tasks involving data analysis:

• Mean (Average): This formula calculates the central tendency of a data set:

  Mean = (ΣX) / N

  where ΣX is the sum of all data points, and N is the total number of data points.

• Standard Deviation: It measures the spread of data points from the mean:

  σ = √(Σ(Xi – μ)² / N)

  where σ is the standard deviation, Xi represents each individual data point, μ is the mean, and N is the total number of data points.

• Variance: The square of the standard deviation:

  Variance = Σ(Xi – μ)² / N

• Simple Linear Regression Equation: Used to model the relationship between two variables:

  Y = β0 + β1X

  where Y is the dependent variable, X is the independent variable, β0 is the intercept, and β1 is the slope.

• Confidence Interval: A range of values that likely contains the true population parameter:

  CI = X̄ ± Z * (σ / √n)

  where X̄ is the sample mean, Z is the Z-score for the desired confidence level, σ is the population standard deviation, and n is the sample size.

• Probability Formula (for binomial distributions): Calculates the likelihood of a specific number of successes in a fixed number of trials:

  P(X = k) = (nCk) * p^k * (1-p)^(n-k)

  where nCk represents the binomial coefficient, p is the probability of success, and k is the number of successes.

Being familiar with these formulas not only aids in solving numerical problems efficiently but also ensures that the methods used are appropriate for the data at hand. Understanding how to manipulate these formulas is essential for interpreting results, making predictions, and drawing meaningful conclusions from data.

Improving Exam Performance in Statistics

Enhancing performance in assessments that involve data analysis requires a combination of strategic preparation, practice, and effective time management. Mastering core concepts and familiarizing yourself with the typical format of such assessments are essential for increasing confidence and achieving better results. A focused approach helps you not only understand the material more deeply but also apply it efficiently under exam conditions.

To boost your results, it is important to identify key strategies that have been proven to help students succeed. These strategies include thorough review, practicing various problem types, and using targeted techniques for time management. Below are some essential tips for improving performance in assessments related to data analysis:

Effective Preparation Strategies

Proper preparation is key to mastering complex material and being ready for assessments. Here are a few strategies to consider:

• Start Early: Begin reviewing the material well in advance to avoid last-minute cramming. This allows time for a deeper understanding of concepts.
• Understand Core Concepts: Ensure that you grasp the fundamental principles, such as data summarization, regression analysis, and hypothesis testing.
• Use Practice Problems: Solve as many practice problems as possible. This helps reinforce concepts and familiarize you with the types of tasks you will encounter.
• Review Mistakes: When practicing, take the time to review mistakes and understand why the correct answers are what they are.

Time Management During the Assessment

Managing your time effectively during the assessment is just as important as preparation. Here are a few tips to help you make the most of your time:

• Prioritize Questions: Start with questions you feel most confident about. This builds momentum and saves time for more challenging ones.
• Allocate Time Wisely: Assign a specific time limit to each section or question, ensuring that you don’t spend too much time on one problem.
• Stay Calm and Focused: Maintain composure throughout the assessment. Stress can impair your ability to think clearly and solve problems efficiently.

Helpful Resources

Using the right resources during your study sessions can greatly enhance your learning experience. Consider incorporating the following tools:

Resource	Purpose
Textbooks and Lecture Notes	Review fundamental theories, formulas, and methods.
Online Practice Tests	Simulate exam conditions and identify areas for improvement.
Study Groups	Collaborate with peers to clarify difficult concepts and solve problems together.
Tutors or Mentors	Seek one-on-one help for personalized guidance on difficult topics.

By implementing these strategies and utilizing the right resources, you can improve your performance in assessments focused on data analysis. Consistent practice, careful preparation, and effective time management are the keys to achieving better results.

Best Practices for Answering Multiple Choice Questions

Mastering the art of tackling multiple-choice assessments requires not only knowledge of the material but also the ability to strategically approach each question. By employing specific techniques, you can increase your chances of selecting the correct option even when uncertain. These strategies focus on effective reading, logical deduction, and time management, which are essential for optimizing performance in multiple-choice formats.

Here are a few best practices to help you navigate through such assessments more efficiently:

Reading and Understanding the Question

Before jumping into selecting an option, it’s crucial to understand the question fully. Avoid rushing through and missing key details. Consider the following tips:

• Carefully Read Each Question: Make sure to read the question carefully, paying attention to words like “always,” “never,” or “sometimes,” as they can alter the meaning.
• Look for Keywords: Identify the key terms in the question to focus your thoughts on the most important aspects of the problem.
• Highlight Key Details: If allowed, underline or highlight critical information within the question to help you remember important points during the process of elimination.

Using Process of Elimination

When you’re unsure of the correct answer, process of elimination is a powerful tool. It helps you narrow down the options by discarding clearly incorrect choices.

• Eliminate Clearly Wrong Answers: Start by identifying any answer choices that are clearly incorrect or irrelevant based on your knowledge of the topic.
• Look for Subtle Differences: Compare remaining options for subtle differences and choose the one that best fits the question’s requirements.
• Don’t Overthink: If you’re stuck between two options, trust your instincts. Often, your first choice is the correct one, so avoid second-guessing too much.

Managing Time Effectively

Proper time management during assessments is essential to ensure that you have enough time to review each question thoroughly. Here are some tips for managing your time:

• Set Time Limits: Allocate a specific amount of time to each question. If you’re stuck on a question, move on and return to it later if you have time.
• Don’t Spend Too Much Time on One Question: If you’re unsure about a question, make your best guess and move forward. Don’t let it consume too much of your time.
• Keep an Eye on the Clock: Regularly check the time to ensure you’re staying on track and not spending too much time on any single section.

By following these best practices, you can approach multiple-choice assessments with confidence and improve your ability to answer correctly, even when faced with challenging material. Preparation, strategic thinking, and careful time management are the cornerstones of success in this format.

Real-World Applications of Business Statistics

Data analysis plays a pivotal role in driving informed decisions across various industries. By applying numerical and analytical techniques, businesses can extract meaningful insights that guide strategic choices, improve operational efficiency, and increase profitability. These methods are used to forecast trends, measure performance, and make data-driven predictions in real-world scenarios.

From marketing to finance, understanding how to interpret and apply data is crucial for success. Here are a few examples of how numerical analysis is utilized in various fields:

Marketing Strategies

In marketing, understanding consumer behavior through data analysis allows companies to create targeted campaigns and improve customer engagement. For example:

• Customer Segmentation: Data is used to group customers based on demographics, buying behavior, or interests, which helps businesses tailor their marketing efforts more effectively.
• Sales Forecasting: Companies analyze past sales data to predict future trends, ensuring they have the right products available at the right time.
• Market Basket Analysis: By analyzing transaction data, businesses can identify product pairings and improve product placement strategies.

Financial Decision Making

In finance, numerical methods are employed to assess risk, determine investment strategies, and optimize portfolios. Common applications include:

• Risk Management: Statistical models are used to measure potential losses, assess the likelihood of different outcomes, and help companies manage financial risks more effectively.
• Credit Scoring: Financial institutions use data models to evaluate an individual’s or company’s creditworthiness based on historical financial data.
• Investment Analysis: Analysts apply statistical techniques to evaluate stock prices, forecast market trends, and guide investment decisions.

Operational Efficiency

Numerical techniques are also widely used in operations to streamline processes, reduce costs, and enhance productivity. Some applications include:

• Quality Control: Statistical methods like Six Sigma are used to monitor production processes, identify defects, and maintain product quality.
• Supply Chain Optimization: Data models help businesses predict demand fluctuations, ensuring inventory levels are optimized to reduce waste and stockouts.
• Workforce Planning: By analyzing employee performance and workforce trends, companies can make decisions about hiring, training, and resource allocation.

In summary, the ability to analyze and interpret data is essential in virtually every field. These techniques allow businesses to make well-informed decisions that enhance their competitive edge, improve customer satisfaction, and optimize operations. From marketing to finance, the real-world applications of data analysis are vast and impactful.

How to Interpret Complex Statistical Data

Understanding intricate data sets can often feel overwhelming, but with the right approach, it becomes a valuable tool for informed decision-making. Proper interpretation involves breaking down the information into manageable parts, identifying patterns, and drawing conclusions that align with the goals of the analysis. Whether you’re working with large datasets or complex results, these steps can help simplify the process and guide accurate interpretations.

The key to analyzing complex data lies in understanding both the numbers and their context. Here are some effective strategies for interpreting detailed datasets:

1. Break Down the Data

The first step in interpreting complex data is to simplify it. Start by identifying the key variables and understanding how they are related to one another. Consider the following:

• Identify Variables: Look for independent and dependent variables, as well as any control variables, to understand the relationships at play.
• Visualize the Data: Use graphs, charts, and tables to transform raw numbers into visual representations, making it easier to spot trends and outliers.
• Summarize Key Metrics: Calculate essential statistics like mean, median, mode, and standard deviation to get an overview of the data distribution.

2. Evaluate the Statistical Significance

Not all data points are equally important. When dealing with complex data, it’s essential to assess the statistical significance of the results. This helps determine whether observed patterns are likely to be real or if they could have occurred by chance. To do this, consider:

• P-Values: A low p-value (typically less than 0.05) suggests that the results are statistically significant and not due to random variation.
• Confidence Intervals: A confidence interval shows the range in which the true value likely falls. Narrow intervals indicate more precise estimates.
• Effect Size: This quantifies the magnitude of a result and helps determine its practical significance in addition to statistical significance.

3. Look for Patterns and Trends

Once the data is broken down and statistical significance is assessed, the next step is to look for trends or patterns that provide insights. This could involve:

• Identifying Correlations: Understanding how variables move in relation to each other can provide important insights. For example, does an increase in one variable correspond with an increase in another?
• Tracking Changes Over Time: Time series analysis can help track how a particular variable evolves over time, revealing long-term trends or cycles.
• Spotting Outliers: Outliers can skew results, so it’s important to investigate unusual data points to determine if they represent significant trends or if they should be excluded from analysis.

4. Contextualize the Results

Finally, interpreting complex data requires placing the findings in the proper context. Understand the conditions under which the data was collected and what external factors might influence the results. Ask yourself:

• What was the purpose of the data collection? Understanding the goals behind the data can help you interpret results more accurately.
• What assumptions were made? Ensure that any assumptions made during the analysis are clearly understood and justified.
• How does the data fit into the bigger picture? Consider how the results align with previous research, industry trends, or expected outcomes.

By following these steps, it becomes easier to break down complex statistical data and make it actionable. Whether you’re working with a simple dataset or a large collection of variables, the key to success is systematic analysis, contextual understanding, and clear interpretation.

Critical Mistakes to Avoid in Statistics Exams

In any assessment of analytical methods, common pitfalls can significantly hinder performance. Understanding and avoiding these errors is essential for achieving a strong understanding of the material and delivering accurate results. By being aware of frequent mistakes, individuals can ensure their answers are well-reasoned and their interpretations are grounded in the correct principles.

1. Misinterpreting Data and Results

One of the most frequent mistakes is misreading or misinterpreting the data provided. This can lead to incorrect conclusions, skewing answers and resulting in a low score. To avoid this:

• Carefully review the given data: Ensure you understand the variables, their relationships, and any specific instructions related to data handling.
• Double-check calculations: Errors in basic arithmetic or formula application can lead to incorrect results. Take extra care with rounding and conversions.
• Context matters: Always interpret results within the context of the question. Numbers alone can be misleading without understanding the bigger picture.

2. Failing to Show Work and Justifications

Simply providing an answer without showing the steps or reasoning can cost valuable points. Even if the correct result is obtained, failure to demonstrate the thought process behind the solution could be considered incomplete. To avoid this:

• Write down every step: Ensure that all working steps, formulas used, and intermediate calculations are clearly shown.
• Explain your reasoning: Justify why certain methods or formulas were used for specific parts of the question.
• Don’t skip intermediate steps: Even if the result seems obvious, it’s important to explain how you arrived at it to avoid penalties for incomplete answers.

3. Ignoring Assumptions and Conditions

Many analytical problems rely on specific assumptions or conditions being met. Failing to acknowledge these can lead to incorrect applications of techniques or inappropriate conclusions. To avoid this:

• Always check assumptions: Before using any statistical method, ensure you know the assumptions required for its proper application (e.g., normality of data, sample size considerations).
• State assumptions explicitly: If a particular assumption is necessary for your method, be sure to state it clearly in your response.
• Adapt to the question’s context: Tailor your answers based on the specific setup of each problem, considering how the context affects the assumptions.

By staying vigilant and avoiding these critical mistakes, you’ll improve both the accuracy of your answers and the clarity of your explanations, which are key to excelling in any analytical assessment. Practice, careful review, and attention to detail will ensure a stronger performance in handling complex data and applying the right methods.