
Developing a strong foundation in analytical reasoning requires dedicated effort and a methodical approach to tackling challenges. Working through structured problems sharpens critical thinking and builds confidence in applying concepts effectively.
Whether preparing for assessments or aiming to refine specific abilities, focusing on targeted tasks can significantly boost understanding. Engaging with diverse scenarios ensures that fundamental principles are mastered and applied with precision in various contexts.
Organized and consistent efforts pave the way for improved performance. With the right resources and guidance, achieving proficiency becomes a manageable and rewarding journey.
Mastering Geometry Through Extra Practice
Achieving proficiency in mathematical reasoning involves consistent effort and the application of effective techniques. By focusing on structured exercises, learners can build a deeper understanding of fundamental concepts and improve their problem-solving skills.
Engaging with well-designed tasks encourages critical thinking and fosters the ability to approach challenges with confidence. These activities serve to reinforce knowledge and ensure that complex ideas become second nature.
With regular application and varied scenarios, individuals can significantly enhance their ability to analyze and solve intricate problems. This method promotes both accuracy and speed, laying a strong foundation for future success.
Key Approaches to Solve Difficult Problems
Overcoming challenging tasks in mathematical reasoning requires strategic thinking and a clear understanding of underlying principles. By breaking down complex scenarios into manageable steps, even the most intricate questions can become approachable.
Analyzing the Problem Thoroughly
Carefully reviewing the question is crucial for identifying the required steps. Understanding relationships between elements and recognizing patterns can provide valuable insights into finding solutions efficiently.
Using Visual Representations
Sketching diagrams or drawing representations helps in visualizing key aspects of a task. This method aids in clarifying relationships and simplifies the interpretation of essential details, ensuring accurate and logical solutions.
Building Confidence in Angle Calculations
Understanding how to work with angles effectively is essential for solving a wide range of mathematical problems. Gaining confidence in this area involves familiarizing oneself with foundational concepts and applying them consistently across various scenarios.
Breaking down complex relationships into simpler components can make calculations more approachable. Recognizing patterns and using logical reasoning ensures accuracy while reducing the likelihood of mistakes. Repeated exposure to different types of tasks further reinforces skills and fosters a deeper understanding of the subject.
By focusing on precision and clarity in every step, learners can develop a strong ability to handle even the most intricate calculations, transforming potential challenges into opportunities for success.
How to Analyze Geometric Proofs
Effectively understanding and evaluating mathematical proofs involves breaking down complex arguments into simpler, logical steps. By recognizing key assumptions and connecting them to the desired conclusion, one can assess the validity of a statement with confidence.
One helpful approach is to identify the given information and the objective. From there, it’s important to choose appropriate theorems or principles to bridge the gap between known facts and the desired outcome. Structuring the proof in clear, organized steps ensures accuracy and clarity.
| Step | Description |
|---|---|
| 1 | Understand the problem and identify given data |
| 2 | Select relevant theorems or postulates |
| 3 | Connect logical steps to reach the conclusion |
| 4 | Review each step for accuracy and coherence |
Breaking Down Shapes for Simpler Solutions
Complex shapes can often be simplified by dividing them into smaller, more manageable parts. By recognizing familiar components within a figure, the problem becomes easier to solve through systematic steps.
Decomposing a figure into basic shapes helps identify key properties, allowing for quicker and more accurate calculations. This method also helps visualize relationships within the figure, making it simpler to apply relevant formulas.
Step-by-Step Breakdown Process
- Identify recognizable basic shapes within the complex figure.
- Divide the shape into smaller sections that can be calculated independently.
- Apply formulas to each smaller shape to find individual measurements.
- Combine the results to obtain the solution for the entire figure.
Examples of Commonly Used Shapes
- Triangles – often used as building blocks for larger polygons.
- Rectangles – easily broken down into smaller areas for calculation.
- Circles – can be divided into sectors for more manageable analysis.
Common Errors and How to Avoid Them

When tackling complex mathematical tasks, certain mistakes are often made due to oversight or misapplication of concepts. Recognizing these common errors can help prevent them and lead to more accurate and efficient solutions.
One of the most frequent errors involves misinterpreting given information or applying the wrong formula. It’s important to ensure that all steps are carefully checked, and logical connections are sound. Reviewing basic principles before starting can prevent miscalculations.
Types of Errors to Watch For
| Error | How to Avoid |
|---|---|
| Incorrect application of formulas | Double-check which formula applies to the situation and ensure all variables are correctly substituted. |
| Misinterpretation of given data | Take time to carefully read and understand the problem before proceeding with calculations. |
| Overlooking units and conversions | Always verify that the units of measurement are consistent and properly converted when necessary. |
Strategies for Preventing Mistakes
- Read the problem carefully and highlight key information.
- Ensure that each step follows logically from the previous one.
- Check all calculations and re-evaluate the final result for consistency.
Learning Effective Techniques for Geometry
Mastering complex mathematical concepts requires adopting efficient approaches that enhance understanding and streamline problem-solving. Developing the right techniques helps tackle challenges with confidence and accuracy.
One of the most effective ways to improve is through the use of visualization and breaking down problems into smaller, manageable parts. Combining theoretical knowledge with practical applications makes it easier to recognize patterns and solve similar problems in the future.
Key Methods for Effective Learning
- Start by understanding fundamental principles and their real-world applications.
- Break down complex problems into simpler components for easier comprehension.
- Use diagrams and drawings to visualize relationships and connections within a problem.
Practicing with Real-Life Examples
- Apply the learned techniques to solve real-world scenarios and practical problems.
- Review different types of problems to identify recurring patterns and strategies.
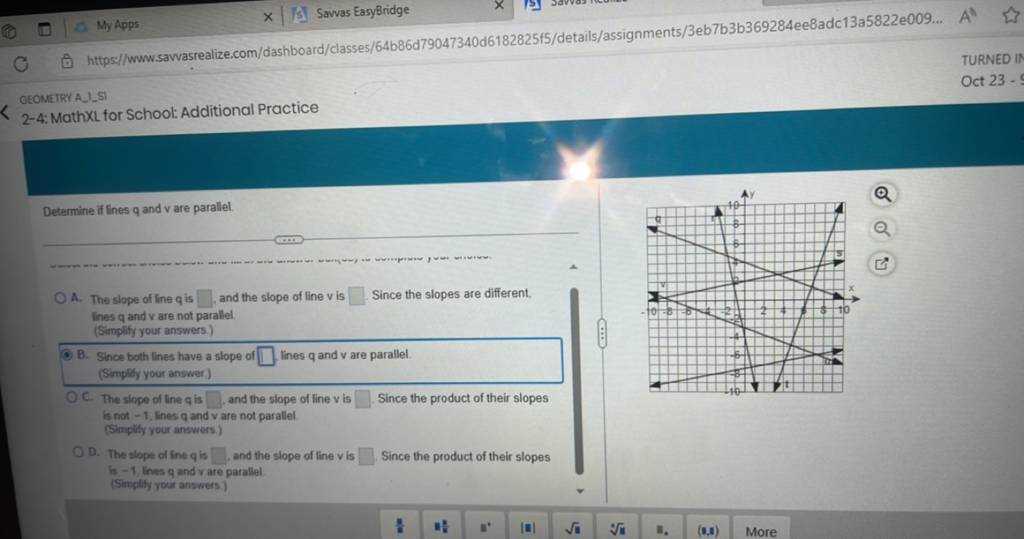
Using Graphs to Understand Geometry Concepts
Graphs are powerful tools that help visualize mathematical relationships and enhance comprehension of spatial concepts. By translating abstract ideas into visual forms, they provide a clear representation of data and can simplify complex problems.
Incorporating graphs into problem-solving allows learners to see how various elements interact, making it easier to grasp concepts like angles, distances, and proportions. Visual aids bring clarity and can guide the process of finding solutions to challenging tasks.
Types of Graphs to Use
- Coordinate graphs for plotting points and understanding spatial relationships.
- Line graphs to represent changes in variables or relationships over time.
- Bar charts to compare quantities and visualize proportions.
Benefits of Graphing in Problem Solving
- Graphs provide a visual aid that can make it easier to identify patterns and relationships.
- They help organize information systematically, reducing errors in calculations.
- Visualizing data on a graph can reveal insights that may not be obvious from numerical expressions alone.
Exploring Real-Life Applications of Geometry
The principles of shapes, space, and measurement are widely used in everyday life, influencing various fields and industries. By understanding these concepts, individuals can solve practical problems that involve designing structures, optimizing spaces, and analyzing patterns.
From architecture to engineering and even nature, the study of spatial relationships plays a crucial role. Real-life applications of these ideas help us improve designs, make informed decisions, and develop technologies that affect our daily lives.
Applications in Architecture and Construction
- Designing buildings and structures with precise measurements.
- Using angles and symmetry to create stable and aesthetically pleasing designs.
- Optimizing floor plans and layouts for efficiency and functionality.
Applications in Nature and the Environment
- Understanding the symmetry and shapes found in plants and animals.
- Using natural patterns to improve ecological designs and sustainability.
- Analyzing landforms and weather patterns through spatial reasoning.
Strengthening Skills in Three-Dimensional Figures
Mastering the understanding of three-dimensional objects is essential for solving a wide range of problems. These figures, which include cubes, spheres, pyramids, and more, are commonly found in real-life applications and abstract reasoning. The ability to analyze their properties, calculate volumes and surface areas, and visualize spatial relationships is critical in fields like design, engineering, and architecture.
By focusing on key concepts such as surface area, volume, and the relationships between different shapes, one can gain a better understanding of how three-dimensional objects fit into various contexts. These skills not only strengthen problem-solving abilities but also enhance the comprehension of complex structures and designs.
Practical Methods to Solve Triangle Problems
Triangles are among the most fundamental shapes in mathematics, and solving problems related to them requires a systematic approach. Whether dealing with angles, side lengths, or area, applying specific strategies helps simplify complex situations. Understanding the key properties of triangles, such as the Pythagorean theorem, trigonometric ratios, and basic geometric principles, allows for more efficient problem-solving.
Utilizing the Pythagorean Theorem
The Pythagorean theorem is a critical tool when working with right triangles. It states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. This formula helps determine unknown side lengths when given enough information about the triangle’s structure.
Applying Trigonometric Ratios

Trigonometry offers a powerful set of tools for solving triangles, especially when dealing with angles and side lengths. Ratios like sine, cosine, and tangent help establish relationships between the sides of a right triangle. By using these ratios in combination with known angle measures, it’s possible to find missing information and solve for unknowns effectively.
Transforming Complex Equations Into Simple Steps
Breaking down intricate mathematical expressions into manageable parts can make solving problems more accessible. By identifying the core components of an equation and applying systematic methods, even the most complicated tasks can be simplified. The goal is to approach each problem methodically, focusing on one step at a time to reach a solution more efficiently.
Identifying Key Variables and Constants
The first step in simplifying any equation is to identify and separate the variables from the constants. Recognizing which elements in the equation are unknowns and which are fixed can provide a clear path forward. This allows for isolating the variable, making the problem easier to solve step by step.
Using Step-by-Step Operations

Once the variables and constants are identified, the next step is to apply the appropriate operations in a logical order. Whether it’s addition, subtraction, multiplication, or division, performing each operation one step at a time ensures that you’re making progress towards a solution without skipping important steps. This methodical approach reduces the risk of errors and allows for clarity throughout the process.