
Success in advanced mathematics requires more than just understanding theory–it involves mastering problem-solving techniques and familiarizing oneself with exam formats. By exploring previous test materials and tackling a variety of mathematical problems, students can enhance their skills and improve their performance on high-stakes assessments. A thorough review of these resources is essential for building confidence and ensuring readiness.
In this section, we provide a comprehensive look at key questions and solutions from past assessments, offering step-by-step explanations and valuable insights. Each solution is crafted to help you identify patterns, understand complex concepts, and develop effective strategies for tackling similar problems in the future.
AP Calc AB Test Solutions and Explanations
When preparing for advanced mathematics assessments, it is crucial to have access to detailed solutions that break down each problem. This section offers an in-depth review of past test questions, focusing on providing clear, step-by-step solutions. Understanding these solutions helps solidify your grasp on key concepts and improves your problem-solving abilities for future tests.
The problems covered here span a wide range of topics, from differentiation to integration and beyond. Each solution is presented with an explanation to ensure that you not only arrive at the correct answer but also comprehend the underlying principles that make the solution work.
- Differentiation Techniques: Learn how to solve rate-of-change problems effectively and master the chain rule, product rule, and quotient rule.
- Integration Methods: Review various integration strategies, including substitution, integration by parts, and partial fractions.
- Area and Volume Calculations: Understand how to compute areas under curves and volumes of solids of revolution using integral calculus.
- Limits and Continuity: Master techniques for finding limits, including L’Hôpital’s rule and limits at infinity.
- Series and Sequences: Delve into the fundamentals of sequences and series, including convergence tests and power series expansions.
By reviewing each solution in detail, you can build a deeper understanding of how to approach similar problems in future assessments. These examples not only guide you through the mechanics of solving the questions but also help develop a more strategic approach to tackling complex problems under time constraints.
Overview of AP Calculus AB Exam
The AP Calculus AB assessment is designed to evaluate students’ understanding of fundamental concepts in mathematics, particularly those involving rates of change and accumulation. It tests a student’s ability to solve problems, apply theoretical concepts, and demonstrate a deep understanding of mathematical principles. This assessment is intended to prepare students for future academic challenges, equipping them with the problem-solving skills required in higher education and various fields of study.
Structured into two main sections, the test evaluates both multiple-choice questions and free-response tasks. The multiple-choice portion assesses a student’s ability to quickly apply concepts, while the free-response section allows for more detailed problem-solving and reasoning. The questions span a broad spectrum of topics, including limits, derivatives, integrals, and their applications in real-world scenarios.
To succeed, students must demonstrate not only their computational skills but also their ability to interpret mathematical results and explain their reasoning clearly. The test is rigorous, but with thorough preparation, it offers an opportunity to showcase a student’s mastery of calculus concepts.
Key Topics Covered in 2012 Exam
The assessment in question evaluates a variety of essential topics in advanced mathematics. These subjects test both theoretical understanding and practical application, focusing on concepts that are fundamental to calculus and its real-world uses. The exam challenges students to demonstrate their ability to solve problems across multiple areas of mathematics, ensuring that they have a well-rounded grasp of the material.
Differentiation and its Applications
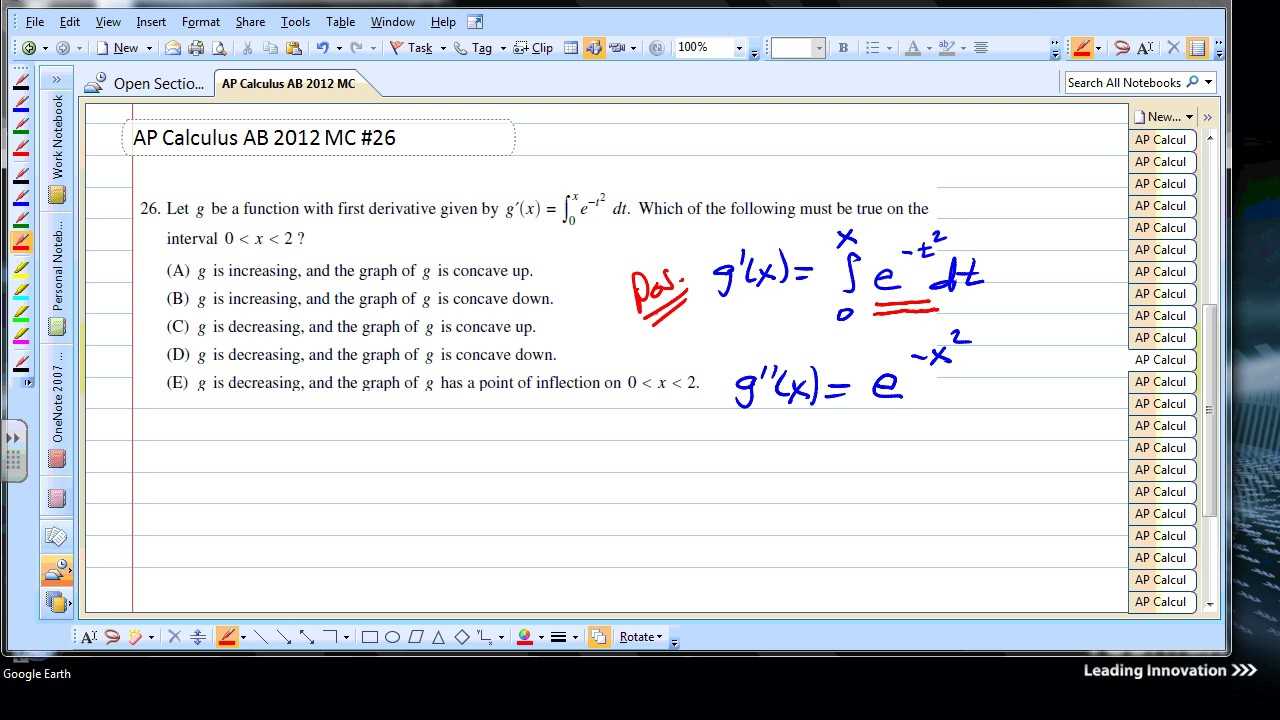
One of the primary areas covered involves differentiation, which is central to understanding rates of change. This includes applying rules such as the chain rule, product rule, and quotient rule to solve a variety of problems. Students are also expected to understand how to apply these concepts in real-world scenarios, such as optimizing functions or finding the slope of a curve at any given point.
Integration and its Real-World Uses
Another key focus is integration, which plays a significant role in calculating areas under curves and solving problems related to accumulation. The exam assesses a student’s ability to apply integration techniques, including substitution and integration by parts, as well as understanding the connection between the fundamental theorem of calculus and real-world situations such as finding displacement or total accumulation over time.
Understanding Multiple Choice Questions

Multiple choice questions are designed to test a student’s ability to quickly apply mathematical principles and solve problems efficiently. These questions require careful reading and a solid understanding of key concepts in order to identify the correct solution from a set of options. Unlike free-response problems, where detailed solutions are required, multiple choice questions focus on evaluating your immediate understanding and decision-making skills.
When tackling these questions, it is important to focus on the wording of each option and eliminate answers that are clearly incorrect. Logical reasoning and an understanding of underlying concepts will often help you narrow down your choices. Additionally, some questions may present distractors–answers that are meant to mislead or test your depth of understanding. By practicing and familiarizing yourself with various types of questions, you can develop strategies to improve accuracy and speed during the assessment.
One of the key techniques is identifying common patterns in questions, such as certain functions or methods that often appear in specific contexts. By doing so, you’ll improve your ability to recognize the most efficient approach to solving the problem at hand. Reviewing sample problems is a great way to reinforce these strategies and boost your confidence in answering multiple choice questions correctly.
Solving Free Response Questions Effectively
Free response questions offer an opportunity to demonstrate a deeper understanding of mathematical concepts by requiring detailed, step-by-step solutions. Unlike multiple-choice questions, where you are given possible answers, these questions ask you to explain your reasoning and show how you arrived at the solution. The key to success lies in organizing your work clearly, using appropriate methods, and thoroughly explaining each step of your process.
Step-by-Step Approach
To tackle free response problems effectively, it’s essential to break the problem into smaller, manageable parts. Begin by carefully reading the problem to identify the given information and what is being asked. Once you have a clear understanding, outline your solution strategy before diving into the calculations. This structured approach will help you avoid unnecessary errors and ensure that all necessary steps are included in your response.
Showing Work and Justifying Solutions

It is crucial to show all steps and justifications for your answers. Simply writing the final solution without explaining how it was obtained can cost valuable points. Make sure to include intermediate steps, such as applying formulas, explaining why a certain method was chosen, and showing the reasoning behind each calculation. This not only helps clarify your thought process but also demonstrates your mastery of the material.
By staying organized and providing thorough explanations, you increase the likelihood of scoring well on free response questions. Remember, these problems assess not just your ability to get the right answer but also your mathematical reasoning and communication skills.
Tips for Time Management During the Exam

Effective time management is crucial when facing a timed assessment. With a limited amount of time to complete multiple sections, it’s essential to approach the test with a strategy that ensures you can answer every question with confidence. Proper planning and execution can help you balance speed with accuracy, allowing you to maximize your score while avoiding unnecessary stress.
Start by quickly assessing the structure of the test. Identify how much time is allocated for each section and allocate your time accordingly. Prioritize questions based on difficulty and point value. It’s often a good idea to tackle the easier questions first, as they will help build momentum and secure quick points. Leave more challenging problems for later, giving yourself the time to think through them thoroughly without feeling rushed.
Another helpful tip is to practice pacing yourself before the actual assessment. Familiarize yourself with typical question formats and practice answering them under timed conditions. This will allow you to gauge how long it takes to solve different types of problems and adjust your strategy as needed. Additionally, make sure to keep an eye on the clock during the test. Regularly check the time to avoid spending too long on any single question.
Lastly, if you find yourself stuck on a particular problem, it’s better to move on and come back to it later, rather than spending excessive time on one question. This will ensure that you have enough time to address all areas of the test without leaving any unanswered questions.
Common Mistakes to Avoid in AP Calculus
When preparing for advanced mathematics assessments, avoiding common pitfalls can make a significant difference in your performance. Many students struggle with certain areas not because they lack knowledge, but because they overlook important details or make simple errors in their calculations. Recognizing these common mistakes and understanding how to avoid them is key to improving accuracy and achieving higher scores.
Misunderstanding Key Concepts
A frequent error occurs when students misinterpret fundamental concepts, such as the difference between instantaneous rate of change and average rate of change. It’s crucial to clearly distinguish between these ideas, as they apply to different types of problems. Another common issue is confusing the various rules for derivatives and integrals. For example, the chain rule or the power rule can easily be applied incorrectly if the problem is not fully understood.
Skipping Steps in Problem-Solving
Many students make the mistake of skipping steps when solving problems in an attempt to save time. While this may seem efficient, it often leads to errors that could have been avoided with careful attention. Showing each step in your work not only helps prevent mistakes but also ensures that you can retrace your reasoning if something goes wrong. Skipping steps also makes it harder to identify where errors have occurred, especially in complex problems.
By paying close attention to detail and avoiding these common mistakes, students can improve both the accuracy and completeness of their solutions, ultimately boosting their overall performance in advanced mathematical assessments.
How to Approach Calculus Word Problems
Word problems in advanced mathematics can initially seem intimidating, but with a systematic approach, they become more manageable. These problems often provide real-world scenarios that require the application of abstract mathematical concepts. The key to solving them effectively is to break down the information presented and translate it into mathematical terms, step by step. Understanding the context and identifying the right approach will help you apply the appropriate techniques with confidence.
Read and Identify Key Information
When faced with a word problem, the first step is to carefully read through the entire question to understand the scenario. Focus on identifying key quantities and relationships that will guide your solution. Highlight or underline important information such as rates, time intervals, and specific values. Additionally, be sure to recognize what the problem is asking for–whether it’s finding a specific value, optimizing a function, or calculating an area. Once you’ve identified these, you can move on to translating them into a mathematical framework.
Set Up the Equation and Solve
After understanding the problem, the next step is to set up an equation that models the situation. This might involve defining variables, applying known formulas, or using concepts like derivatives or integrals. Once the equation is in place, you can solve it using the appropriate methods. Remember to take your time and work through the solution logically. If you encounter difficulties, it’s helpful to check your assumptions and revisit the steps to ensure that no important details were overlooked.
By approaching word problems in a structured and thoughtful manner, you’ll improve your ability to apply mathematical concepts in practical situations and increase your chances of finding the correct solution.
Breakdown of 2012 Exam Sections
The structure of a timed assessment in advanced mathematics typically includes multiple sections designed to test a range of skills. Each section evaluates specific abilities, from solving basic problems to applying advanced concepts in real-world scenarios. Understanding the distribution of questions across sections helps students approach the test strategically, ensuring that they allocate time and effort according to the importance of each segment.
Multiple Choice Section

The multiple-choice section is intended to quickly assess a student’s foundational understanding of key principles. These questions often cover a broad range of topics, requiring a combination of quick thinking and strong recall of formulas and methods. The challenge lies in identifying the correct answer from a set of options, often with similar-looking distractors. Time management is crucial in this section, as it’s designed to be completed quickly. Focus on answering the easier questions first to build confidence before tackling the more complex ones.
Free Response Section
In contrast to the multiple-choice questions, the free-response section allows students to demonstrate their ability to apply concepts in more depth. These questions require detailed solutions, with each step of the reasoning process shown clearly. Problems in this section might involve higher-level problem-solving, such as optimization, rates of change, or area under curves. The free-response section not only tests mathematical knowledge but also the ability to communicate solutions effectively. Careful organization of work and clear justification of each step are essential for success.
By understanding the distinct nature of each section and allocating time wisely, students can ensure a well-rounded approach to tackling the full assessment and performing to the best of their abilities.
Answer Key for AP Calc AB 2012
After completing an advanced mathematics assessment, reviewing the correct solutions is an essential part of the learning process. The answer key provides students with the opportunity to check their work and identify areas where they may have made mistakes or missed key steps. By comparing their answers to the correct ones, students can gain a deeper understanding of the concepts tested and improve their problem-solving strategies for future assessments.
Key Solutions Overview
The following table provides the correct solutions for each section of the assessment. It breaks down the answers for both multiple-choice and free-response questions, offering clarity on where each solution comes from and how to approach similar problems in the future.
| Question Number | Correct Answer | Explanation |
|---|---|---|
| 1 | A | This problem tested the application of the chain rule. The correct derivative was found by applying the proper steps to the composite function. |
| 2 | B | The question involved solving for the area under a curve. The integral was set up correctly, and the correct limits of integration were applied. |
| 3 | C | This free-response question required optimization. By finding the critical points and testing the boundaries, the maximum was identified. |
| 4 | D | A related rates problem was solved here by correctly differentiating both sides of the given equation with respect to time. |
| 5 | A | This question asked for the evaluation of a definite integral. The solution involved correctly applying the Fundamental Theorem of Calculus. |
Additional Insights

It’s important to not just look at the final answer but also understand the reasoning behind each solution. Going over the steps in the provided explanations will help reinforce the methods used and ensure a deeper understanding of the material. Taking the time to review these answers critically can help strengthen your approach to similar problems in the future.
Step-by-Step Solutions to Problems
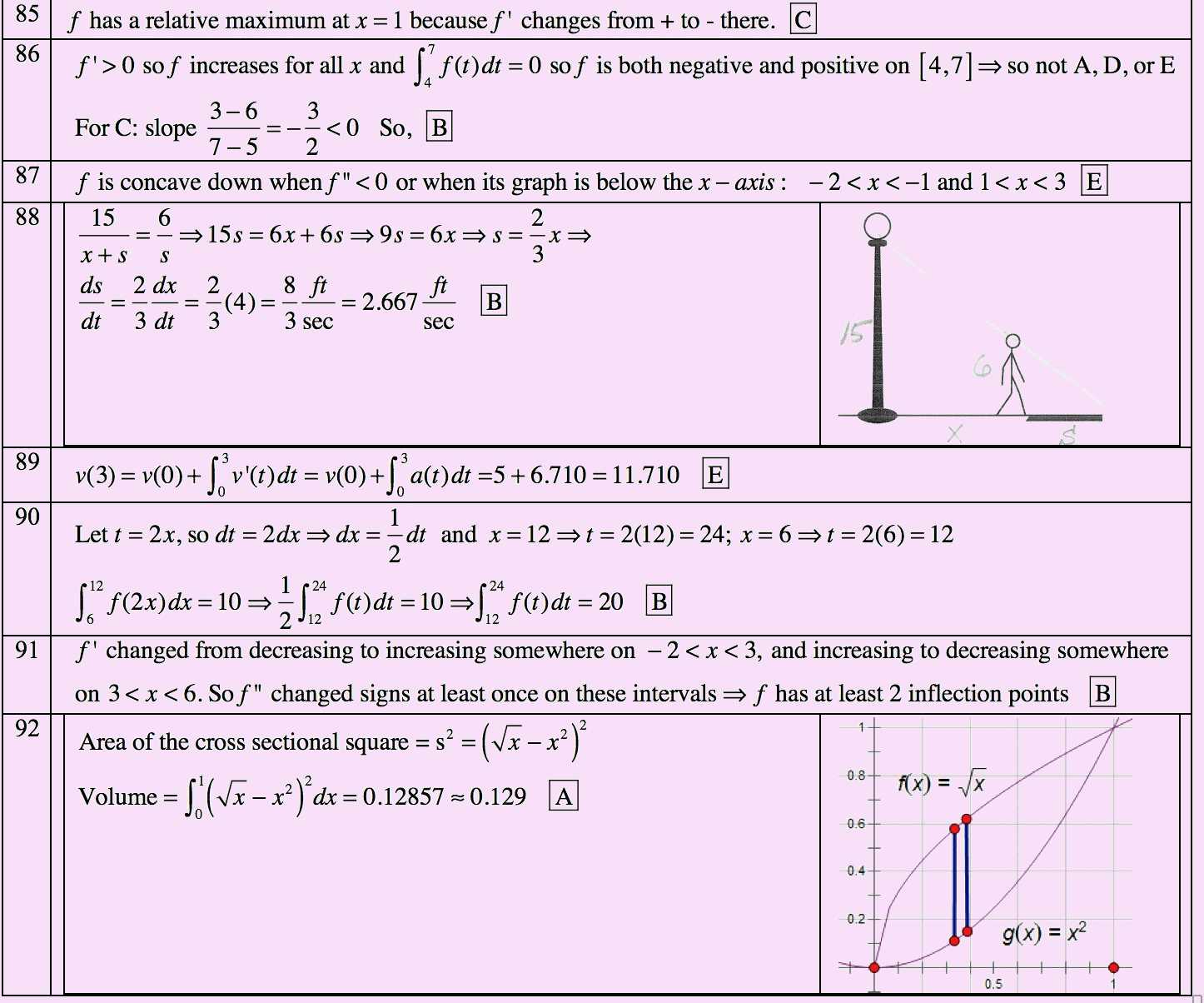
Understanding the process behind solving mathematical problems is crucial for mastering the subject. A step-by-step solution not only helps break down complex problems into manageable parts but also reinforces the logical flow of each operation. By following these solutions carefully, students can gain insights into various techniques and approaches, allowing them to tackle similar challenges with greater ease in the future.
Problem 1: Finding the Derivative of a Function

To find the derivative of the given function, the following steps are applied:
- Step 1: Identify the type of function (e.g., product, quotient, composite) to determine the appropriate rule for differentiation.
- Step 2: Apply the derivative rule (e.g., chain rule, power rule) to differentiate each term in the function.
- Step 3: Simplify the expression after applying the differentiation rules. Ensure all terms are correctly simplified.
- Step 4: Double-check the calculations to ensure accuracy, particularly for any terms that require special attention.
By following these steps, the derivative of the function can be determined, ensuring a comprehensive understanding of the process.
Problem 2: Solving an Area Under the Curve
For finding the area under a curve, the solution involves the following steps:
- Step 1: Set up the integral with the correct limits of integration, based on the region defined in the problem.
- Step 2: Integrate the function using the appropriate methods (e.g., substitution, integration by parts).
- Step 3: Apply the limits of integration and evaluate the definite integral to find the area.
- Step 4: Verify the results to ensure that the area calculation is accurate and aligns with the expected outcome.
Following these steps helps ensure that the process of finding areas under curves is done methodically and correctly.
Important Formulas for AP Calculus
Mastering fundamental equations and formulas is key to performing well in advanced mathematics. These expressions provide the foundation for solving a wide range of problems, from finding derivatives to evaluating integrals. Familiarity with these formulas enables students to approach problems with confidence and accuracy, ensuring that they can tackle even the most complex questions efficiently.
Derivative and Integral Formulas
The following formulas are crucial for understanding the relationship between functions and their rates of change. They form the backbone of calculus and should be thoroughly memorized and applied in various contexts:
- Power Rule for Differentiation: If f(x) = x^n, then f'(x) = n * x^(n-1).
- Product Rule for Differentiation: If f(x) = g(x) * h(x), then f'(x) = g'(x) * h(x) + g(x) * h'(x).
- Quotient Rule for Differentiation: If f(x) = g(x) / h(x), then f'(x) = [g'(x) * h(x) – g(x) * h'(x)] / [h(x)]^2.
- Fundamental Theorem of Calculus: If F(x) is the antiderivative of f(x), then ∫[a to b] f(x) dx = F(b) – F(a).
Applications of Formulas in Real Problems
Once you are familiar with the essential formulas, applying them to real-world problems becomes easier. Whether you are calculating the area under a curve, solving for maximum or minimum values, or dealing with related rates, these formulas are indispensable. Remember that the key to mastering calculus is not just knowing these formulas but understanding how to apply them correctly in different contexts.
Calculus Concepts to Master Before the Exam
To perform well in advanced mathematics, it is essential to have a strong grasp of core concepts that form the foundation of the subject. Understanding these principles will not only help in solving problems but also ensure a deeper insight into the subject. The following are key concepts that every student should master before facing the test.
Key Concepts to Focus On
- Limits: Understanding how functions behave as they approach a specific value is fundamental. Practice evaluating limits using various techniques like direct substitution, factoring, and L’Hôpital’s rule.
- Derivatives: Mastering how to compute the rate of change of a function is crucial. Focus on rules like the power rule, product rule, quotient rule, and chain rule.
- Integrals: Be comfortable with both indefinite and definite integrals. Practice finding areas under curves and using techniques like substitution and integration by parts.
- Related Rates: These problems involve multiple variables that change over time. Understanding how to relate different rates of change will be useful for solving real-world problems.
- Optimization: Be able to identify and solve maximum and minimum problems. Learn how to use derivatives to find critical points and analyze the behavior of functions.
- Series and Sequences: Understand the basics of convergence, divergence, and how to work with series expansions.
Strategies for Mastery
- Practice Regularly: Continuous practice will reinforce these concepts and ensure you can recall them under pressure.
- Understand Theorems and Proofs: Understanding why certain rules work can give you a deeper understanding and help in applying them correctly.
- Work Through Real Problems: Applying these concepts to practical scenarios will solidify your understanding and prepare you for any type of question.
Focusing on these concepts and mastering them before the test will give you the confidence needed to approach any problem effectively.
Exam Strategies for Higher Scores
Achieving a higher score on an advanced mathematics assessment requires more than just knowledge of the material. Effective strategies can help manage time, reduce stress, and increase accuracy under pressure. Here are key approaches to enhance your performance and boost your score.
- Time Management: Allocate a specific amount of time to each section of the test and stick to it. If you get stuck on a question, move on and return to it later to avoid wasting valuable time.
- Read Carefully: Pay close attention to the wording of each question. Many problems contain subtle details or specific instructions that can make the difference between a correct and incorrect answer.
- Start with What You Know: Begin with the questions you feel most confident about. This will build your momentum and give you more time for challenging problems.
- Show Your Work: Even if you are confident in your answer, writing down your steps clearly can help ensure you don’t miss key points and can earn partial credit if necessary.
- Stay Calm and Focused: Maintain a calm mindset throughout the test. Take deep breaths and stay focused, even if you encounter difficult questions.
- Review Your Answers: If time allows, review your answers to check for any mistakes or missed steps. Often, small errors can be caught upon a second review.
By incorporating these strategies into your preparation and during the test, you can improve both your performance and confidence, ultimately achieving better results.
Resources for Additional Practice
For those looking to deepen their understanding and refine their problem-solving skills, several resources can provide valuable extra exercises and explanations. Engaging with these materials regularly can help reinforce concepts, develop strategies, and build confidence for any advanced mathematical assessment.
- Online Problem Solvers: Websites like Khan Academy and Wolfram Alpha offer a wide range of interactive exercises with step-by-step solutions. These platforms are great for practicing different types of problems at your own pace.
- Textbooks and Workbooks: Many textbooks and specialized workbooks designed for advanced mathematics contain numerous exercises and practice sets. These often include detailed solutions, making them an excellent resource for mastering difficult topics.
- Video Tutorials: YouTube channels such as PatrickJMT and Professor Leonard provide in-depth video tutorials on various topics, allowing you to see problems being solved in real-time.
- Mobile Apps: Apps like Photomath and Microsoft Math Solver can be useful for quick problem-solving assistance and for practicing on the go.
- Study Groups: Collaborating with peers in study groups can provide insight into different problem-solving methods. Sometimes discussing challenging problems with others can lead to new strategies and clearer understanding.
- Practice Tests: Many websites and educational platforms offer downloadable practice tests, similar to the official ones. Completing these under timed conditions will help you become more familiar with the test format and improve time management skills.
Consistent engagement with these resources will help reinforce your understanding, ensuring that you are well-prepared for any challenges that may arise.
How to Review After the Exam
Reviewing your performance after a challenging assessment is essential for identifying areas of strength and pinpointing opportunities for improvement. A systematic review process not only helps reinforce your understanding but also allows you to learn from any mistakes made during the test. Reflecting on your performance can guide future study habits and enhance your ability to solve problems efficiently in similar contexts.
Steps for Effective Post-Test Review
- Identify Mistakes: Carefully go through the problems you struggled with. For each one, analyze the solution process and pinpoint where you went wrong–was it a misunderstanding of the concept, a miscalculation, or a time management issue?
- Understand Correct Solutions: Review the correct solutions thoroughly. Try to comprehend each step of the process and the reasoning behind it. This will help you recognize any gaps in your knowledge.
- Focus on Problem Types: Take note of the types of problems that were most challenging. These could be specific types of equations, applications of certain rules, or problems requiring multi-step solutions. Target these areas in future study sessions.
- Analyze Time Management: Reflect on how well you managed your time during the test. Were there questions that took longer than expected? Did you rush through some sections? This reflection will help improve your time allocation in future assessments.
Organizing Your Review for Maximum Effectiveness
To ensure your review process is as productive as possible, it helps to keep track of common problem areas and patterns. Below is a suggested method for categorizing your mistakes:
| Category | Common Mistakes | Actions to Improve |
|---|---|---|
| Conceptual Errors | Misunderstanding key principles or rules | Revisit theory and do additional exercises focused on that concept |
| Calculation Errors | Simple arithmetic or algebraic mistakes | Practice with more examples and check work carefully |
| Time Management | Spending too much time on certain problems | Take timed practice tests to improve speed and decision-making |
By actively reflecting on your performance, you can turn any setbacks into learning opportunities, strengthening both your understanding and test-taking strategies for the future.
Preparing for the Next AP Exam

Successfully preparing for a challenging assessment requires consistent effort, strategic planning, and an understanding of the material. Rather than cramming information at the last minute, the most effective preparation involves setting clear goals, managing your study time, and practicing the skills you’ll need to apply during the test. Focusing on areas where you can improve and reinforcing your strengths will help ensure you’re ready for the upcoming challenge.
Effective Study Techniques
- Create a Study Plan: Organize your study sessions well in advance. Break down the material into manageable chunks and assign specific topics to each session. Stick to this plan for consistent progress.
- Practice Regularly: Regular practice is key to reinforcing concepts. Aim to solve problems daily, focusing on areas you find most challenging.
- Utilize a Variety of Resources: Rely on different resources such as textbooks, online materials, video tutorials, and past assessments to deepen your understanding of complex topics.
- Work with Study Groups: Collaborating with peers can be beneficial. Discussing difficult problems and explaining concepts to others can solidify your own knowledge.
Time Management and Test-Taking Strategies
- Simulate Test Conditions: Take full-length practice assessments under timed conditions to simulate the pressure of the real test. This will help you manage time effectively during the actual exam.
- Prioritize High-Yield Topics: Review key topics that have historically been emphasized on assessments. Focus on mastering these areas to maximize your score potential.
- Review Mistakes: After each practice session, take time to review your mistakes. Identify the reasons for incorrect answers and make sure you understand the correct approaches to those problems.
- Relax and Rest: Avoid burnout by ensuring you have adequate rest. A well-rested mind performs better under pressure, so don’t underestimate the importance of sleep before the test.
With a structured approach and consistent effort, you can feel confident and prepared for the upcoming assessment. Focus on strengthening your weaknesses, refining your problem-solving techniques, and maintaining a positive mindset as the test day approaches.
Feedback from Students on 2012 Assessment
After completing a significant evaluation, students often share valuable insights and experiences that can help others understand the challenges and expectations of the test. Feedback from previous years can highlight areas that are frequently perceived as difficult, as well as strategies that proved to be effective. By reviewing student comments, future test-takers can better prepare and adjust their study techniques accordingly.
Common Student Reactions

- Time Pressure: Many students mentioned feeling rushed during the assessment, particularly in sections requiring detailed problem-solving. Managing time effectively was a common challenge, especially when questions were more complex.
- Topic Variety: Several students noted that the content covered a wide range of topics, from fundamental concepts to more advanced applications. This variety made it necessary to be well-prepared across all areas of the curriculum.
- Question Difficulty: While some felt certain questions were straightforward, others found the more advanced problems to be challenging, requiring deep understanding and a strong grasp of specific techniques.
- Mathematical Notation and Language: A number of students expressed difficulty with interpreting some of the terminology and symbols used in questions, emphasizing the importance of familiarizing oneself with all relevant mathematical notation.
What Worked for Students
- Focused Review: Many students recommended spending time on areas they found most challenging, with targeted practice helping them feel more confident during the test.
- Practice under Time Constraints: Simulating test conditions by practicing under time constraints helped some students manage the pressure and improve their pacing during the actual assessment.
- Group Study: Several students found it beneficial to work with peers, as discussing complex topics and solving problems together clarified difficult concepts and provided diverse perspectives.
- Relaxation Techniques: Some students emphasized the importance of staying calm and composed. Taking breaks, practicing deep breathing, and maintaining a positive mindset were strategies they used to keep stress at bay.
Overall, while the evaluation posed challenges, students found that preparation, practice, and collaboration were key to overcoming obstacles. The insights gained from their feedback can guide future candidates in making strategic decisions for their own success.