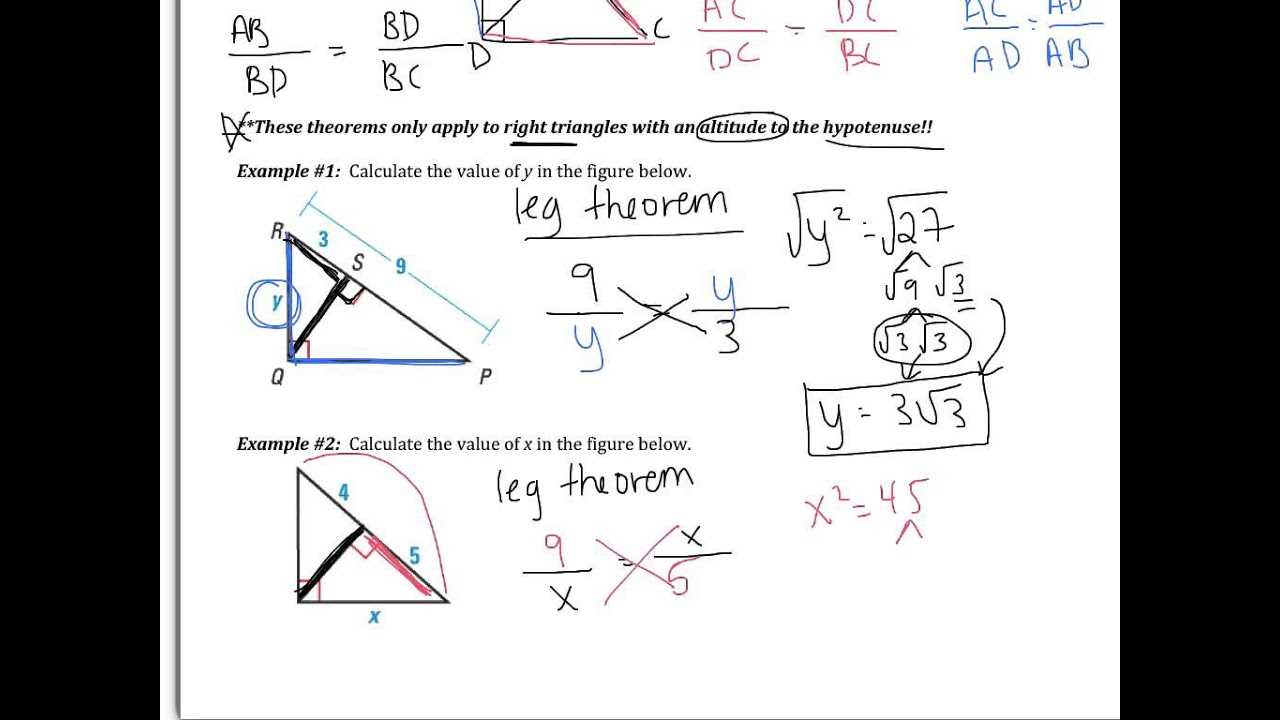
In any mathematical curriculum, tackling problems that involve spatial reasoning, measurement, and calculation is fundamental to building a strong foundation. These exercises require a clear understanding of the principles that govern shapes, sizes, and their relationships. While the complexity of the problems can vary, the key to success lies in applying logical steps and using the right strategies to arrive at accurate solutions.
Effective problem-solving often begins with breaking down each question into manageable parts. By focusing on one aspect at a time, students can avoid feeling overwhelmed and stay on track. Whether the task involves calculating distances, angles, or areas, every step plays a critical role in reaching the correct conclusion. Understanding these principles can enhance one’s ability to solve even the most challenging problems with ease.
Success in this field also comes from practice and familiarity. As learners encounter different types of questions, they develop a better sense of the tools and methods required for each. This process fosters a deeper understanding of mathematical relationships, making it easier to tackle future challenges with confidence.
Practice B Geometry Answers Overview
This section focuses on the key concepts and techniques needed to solve mathematical problems related to spatial relationships and measurement. The goal is to provide a comprehensive guide to the exercises, offering clear solutions and explanations that will help students master the necessary skills. With a solid grasp of these fundamental ideas, learners can approach complex problems with greater ease and confidence.
Essential Problem-Solving Techniques
To tackle these types of questions effectively, it’s crucial to follow a systematic approach. Here are some techniques that will help you break down each task:
- Identify the given information and what needs to be determined.
- Visualize the problem by drawing diagrams or sketches to clarify relationships between elements.
- Apply appropriate formulas and rules to solve the problem step by step.
- Check your work to ensure accuracy and correctness of the solution.
Common Question Types
The exercises often involve different kinds of problems, which may require varying strategies. Some common types include:
- Angle calculations: Determining the size of angles formed by intersecting lines or shapes.
- Area and perimeter: Calculating the area or perimeter of various shapes, including triangles, quadrilaterals, and circles.
- Distance and congruence: Understanding the relationships between distances and determining if figures are congruent or similar.
By practicing these types of problems, learners can become more familiar with the patterns and methods that will help them solve similar tasks in the future.
Understanding Key Geometry Concepts
Mastering the fundamentals of spatial reasoning and measurement is crucial for solving problems involving shapes, sizes, and their relationships. A deep understanding of these concepts enables individuals to approach various mathematical challenges with confidence. These foundational principles form the backbone of more complex tasks and allow for accurate problem-solving in different contexts.
Shapes and their properties are central to this field. Knowing the characteristics of basic figures such as triangles, quadrilaterals, and circles is essential. Understanding how angles, sides, and symmetry interact within these figures helps to form a solid base for tackling more advanced topics.
Relationships between elements also play a critical role. Whether it’s the relationship between angles in intersecting lines or the connection between sides and diagonals in polygons, recognizing these links is key to unlocking solutions. By applying these concepts systematically, you can solve complex problems more efficiently and accurately.
Step-by-Step Solutions for 7.3 Problems
When solving mathematical problems involving spatial relationships and measurement, following a structured approach is essential. By breaking down each problem into smaller, more manageable steps, you can ensure that no detail is overlooked. This method allows for a clear path to the solution and helps avoid common errors that can arise during more complex calculations.
The key to effective problem-solving lies in understanding the given information and applying the appropriate formulas. Start by identifying what is known and what needs to be determined. Then, use diagrams or sketches to visualize the relationships between the elements involved. After that, apply the correct mathematical operations in a logical sequence, making sure to check your work at each step.
For each problem, it is important to approach the solution with a focused mindset, ensuring that all steps are carried out precisely. This structured method not only makes it easier to solve individual tasks but also helps develop a deeper understanding of the underlying principles, which will aid in solving more advanced problems in the future.
Common Mistakes to Avoid in Geometry
When tackling problems related to shapes, sizes, and their properties, certain errors are frequently made that can hinder progress and lead to incorrect solutions. Recognizing and understanding these common mistakes is essential for improving accuracy and efficiency in mathematical tasks. By being aware of these pitfalls, learners can avoid them and approach each problem with greater confidence.
| Common Mistake | How to Avoid It |
|---|---|
| Misinterpreting the given information | Carefully read the problem and underline or highlight key details to ensure nothing is overlooked. |
| Forgetting to apply correct formulas | Write down all relevant formulas before starting the problem and refer to them throughout the solution process. |
| Neglecting to check calculations | Always review your calculations step by step to catch any errors before finalizing the solution. |
| Overlooking geometric relationships | Draw diagrams or use visual aids to clearly see how the elements of the problem are connected. |
| Assuming symmetry without verification | Verify symmetry or congruence conditions before applying properties that depend on these relationships. |
By actively avoiding these common mistakes, students can enhance their problem-solving abilities and improve their understanding of key mathematical concepts. Practicing careful attention to detail is crucial in ensuring accurate results and building a strong foundation for more advanced topics.
How to Approach Practice B Questions
When facing mathematical exercises that involve spatial reasoning and problem-solving, it’s essential to develop a structured approach. A clear and logical method will not only help you find the correct solution but also improve your understanding of the underlying concepts. By breaking down each question into manageable steps, you can navigate through complex tasks more efficiently.
| Step | Action |
|---|---|
| 1. Analyze the problem | Read the question carefully and identify the known information and what needs to be found. |
| 2. Visualize the situation | Draw a diagram or sketch to represent the problem, ensuring you understand the relationships between the elements. |
| 3. Apply relevant principles | Use the appropriate formulas, properties, or theorems that relate to the problem you’re solving. |
| 4. Work through the steps | Proceed step-by-step, performing calculations or logical deductions, and check your progress as you go. |
| 5. Review your solution | Once you reach a solution, verify your work to ensure there are no errors or overlooked details. |
Following this methodical process will help ensure that each question is approached in an organized and effective way. By mastering these steps, you can solve problems more efficiently and deepen your understanding of the concepts involved.
Breaking Down Geometry Formulas
Mathematical formulas are essential tools for solving problems involving shapes, measurements, and spatial relationships. Understanding how each formula is derived and how to apply it is key to mastering these types of tasks. Rather than simply memorizing equations, it’s important to break them down into their components and understand the role each part plays in the calculation.
Key Components of a Formula
Formulas typically consist of variables, constants, and operations. Each component serves a specific function in the process of solving a problem. Here’s how to approach them:
- Variables: These represent unknown quantities or measurements that need to be determined.
- Constants: Fixed values that do not change, such as pi (π) in circular calculations.
- Operations: Mathematical actions such as addition, subtraction, multiplication, and division that connect the variables and constants.
Understanding Common Formulas
By breaking down common formulas used for perimeter, area, and volume, you can better understand their structure and how to apply them to different problems. For example:
- For the area of a rectangle, A = l × w, where l is the length and w is the width.
- For the area of a circle, A = πr², where r is the radius and π is approximately 3.1416.
- For the volume of a sphere, V = (4/3)πr³, where r is the radius of the sphere.
Understanding the relationships between the elements in each formula allows for more flexible and accurate problem-solving, especially when the question involves multiple steps or more complex shapes.
Analyzing Problem Types in Practice B
When working through mathematical exercises, it’s crucial to recognize the different types of problems you may encounter. Understanding the structure of each problem allows you to apply the right strategies and techniques to solve them efficiently. By analyzing the types of questions, you can better anticipate what steps need to be taken and which concepts should be applied.
There are several common problem categories that often appear in exercises related to shapes, measurements, and spatial reasoning. Recognizing these categories can help streamline your approach and ensure that you’re using the appropriate methods to find the solution.
Common Problem Types
- Measurement problems: These questions require you to find the dimensions, area, or volume of geometric shapes, such as rectangles, circles, or spheres.
- Angle calculations: These problems involve determining unknown angles within intersecting lines or polygons. Key techniques include using angle relationships such as complementary or supplementary angles.
- Congruence and similarity: These problems focus on determining whether two shapes are congruent or similar based on their sides, angles, and proportional relationships.
- Coordinate-based problems: These exercises ask you to find distances, midpoints, or slopes between points on a coordinate plane.
Approaching Each Problem Type

Each category requires a slightly different approach:
- For measurement problems, always begin by identifying the dimensions you know and apply the correct formula for area or volume.
- For angle calculations, first identify any given angle relationships and use properties such as the sum of angles in a triangle or straight line.
- For congruence and similarity questions, check for equal sides, equal angles, and proportional relationships between corresponding parts.
- For coordinate-based problems, make sure to apply the distance formula or midpoint formula correctly based on the points provided.
By recognizing the type of problem you’re facing and adjusting your approach accordingly, you can solve each exercise more effectively and accurately.
Tips for Improving Geometry Skills
Mastering spatial reasoning and the ability to work with shapes and measurements takes practice and focus. Whether you’re looking to improve your understanding of specific concepts or boost your problem-solving speed, adopting a systematic approach can significantly enhance your skills. By focusing on key strategies and making them part of your regular study routine, you can strengthen your ability to tackle even the most complex tasks with confidence.
Effective Strategies for Skill Enhancement
- Practice regularly: Consistent practice is the key to improvement. Work through a variety of problems to develop familiarity with different concepts and approaches.
- Visualize problems: Create diagrams, drawings, or models to help you better understand the relationships between different elements in the problem.
- Break down complex problems: Divide complicated tasks into smaller, manageable steps to avoid feeling overwhelmed and to ensure accuracy.
- Review key formulas: Regularly revisit essential formulas and theorems to keep them fresh in your mind and ensure you apply them correctly.
Building Confidence Through Practice
In addition to understanding the concepts, it’s important to build your confidence by approaching problems step by step. As you gain experience, you will become more comfortable recognizing patterns, making quicker decisions, and identifying the best strategies for solving different types of questions.
- Start with easier problems and gradually progress to more challenging ones as your skills improve.
- Focus on understanding the “why” behind each formula or concept, not just memorizing the rules.
- Seek help when needed–collaborating with peers or instructors can offer new insights and approaches to difficult problems.
With time, effort, and a focus on the basics, you can continually improve your spatial reasoning and problem-solving abilities. Keep practicing and applying these strategies, and you’ll find that your skills will grow steadily.
Strategies for Solving Complex Problems
Tackling difficult problems requires a combination of critical thinking, organization, and strategic planning. By breaking down complex tasks into smaller, more manageable steps, you can approach them with confidence and clarity. The key is to remain focused and methodical, applying the right techniques to navigate through the layers of the problem effectively.
Step-by-Step Problem Solving
One of the most effective approaches to solving challenging problems is to divide the task into clear stages. Here’s how you can approach each problem:
- Understand the problem: Carefully read the problem statement and identify the given information and what is being asked.
- Break it down: Divide the problem into smaller parts, identifying relationships and constraints between different elements.
- Choose the right method: Select the appropriate formula, principle, or approach based on the problem’s nature. This could involve using algebraic techniques, geometric properties, or logical reasoning.
- Execute the plan: Start solving the problem step by step, showing all your work to minimize mistakes.
- Review your solution: Once you reach a result, verify the answer and ensure all parts of the problem have been addressed.
Techniques for Handling Difficult Questions
For particularly challenging problems, there are additional strategies to help you make progress:
- Work backward: Sometimes, starting from the desired solution and retracing your steps can help you uncover the necessary steps to reach the answer.
- Look for patterns: Identify repeating structures or symmetries that might simplify the problem or give clues about how to approach it.
- Use estimation: Estimating a range of possible values can help you check if your final answer is reasonable and guide you if you’re stuck.
- Draw diagrams: Visual representations can often reveal relationships and connections that aren’t immediately obvious in a purely algebraic form.
By combining these strategies and remaining patient, you can improve your ability to solve even the most complex problems with accuracy and efficiency.
Real-Life Applications of Geometry Concepts
The principles of spatial reasoning and measurements are not confined to textbooks. They are widely applied in many fields that impact our daily lives, from construction to technology, and even art. Understanding these concepts allows individuals to solve real-world problems with precision, whether designing a building, navigating a city, or creating digital models. Geometry plays a crucial role in helping professionals make informed decisions and optimize their work.
Key Areas Where Spatial Concepts Are Used
- Architecture and Construction: Architects and builders use spatial reasoning to design structures, ensuring that buildings are not only aesthetically pleasing but also structurally sound. From calculating load-bearing walls to determining material quantities, geometry is essential in the planning and construction phases.
- Navigation and Mapping: When traveling or using GPS systems, the understanding of distances, angles, and scales helps people accurately navigate across different terrains. Mapping services rely on geometric calculations to plot precise routes and estimate travel times.
- Art and Design: Artists and designers apply principles like symmetry, proportion, and perspective to create visually appealing works. From graphic design to sculpture, geometry influences the way objects are proportioned and arranged in space.
- Technology and Engineering: In fields like robotics, game development, and computer-aided design (CAD), spatial understanding is vital for creating models, simulating movements, and optimizing solutions for complex technical problems.
- Astronomy: Astronomers use geometric principles to calculate distances between celestial bodies, analyze planetary motion, and map the universe. Geometry helps in understanding the vast expanses of space and the positioning of objects within it.
How Geometry Improves Efficiency and Accuracy
In each of these fields, geometry is not just theoretical knowledge, but a tool that directly impacts outcomes. The ability to measure, analyze, and calculate shapes and spaces allows professionals to make better decisions and avoid costly errors. From precise measurements in manufacturing to the optimization of flight paths in aviation, geometry helps in refining processes, saving time, and enhancing safety.
By recognizing the real-world applications of spatial reasoning, individuals can better appreciate the value of mastering these concepts, knowing they are integral to both practical and creative endeavors in various industries.
Geometry Vocabulary for Practice B
Understanding the key terms and definitions is crucial for solving problems effectively. The language used in spatial reasoning and measurements provides the foundation for interpreting questions and applying concepts correctly. Familiarizing yourself with the most important terminology will help you approach challenges with confidence and clarity. Below is a list of essential vocabulary that will aid in mastering these concepts.
| Term | Definition |
|---|---|
| Angle | A figure formed by two rays (sides) that share a common endpoint (vertex). Angles are measured in degrees. |
| Perimeter | The total length of the boundaries of a two-dimensional shape. It is calculated by adding the lengths of all sides. |
| Area | The measure of the surface enclosed by a shape, expressed in square units. Common formulas depend on the type of shape (e.g., length x width for a rectangle). |
| Volume | The amount of space occupied by a three-dimensional object, measured in cubic units. |
| Parallel lines | Two or more lines that run in the same direction and remain the same distance apart, never meeting. |
| Perpendicular lines | Two lines that intersect at a right angle (90 degrees). |
| Radius | The distance from the center of a circle to any point on its circumference. |
| Diameter | The distance across a circle, passing through the center. It is twice the length of the radius. |
| Symmetry | The property of an object or shape that is the same on both sides when divided by a central line or point. |
| Congruent | Two shapes that are identical in shape and size, but possibly rotated or reflected. |
Mastering these terms and their meanings is essential for understanding how different elements relate to each other within problems. With a solid vocabulary foundation, it becomes easier to comprehend instructions, recognize patterns, and apply the correct formulas when necessary.
Visualizing Geometry Problems Effectively
One of the most powerful strategies for tackling complex spatial problems is the ability to visualize them clearly. By creating mental images or drawing diagrams, you can better understand the relationships between shapes, angles, and lines. This approach allows you to break down a problem into manageable parts, making it easier to apply the correct formulas and identify key elements needed for a solution. Visualization also aids in recognizing patterns that might not be immediately obvious from the problem statement alone.
Techniques for Effective Visualization

There are several methods that can help improve your ability to visualize and solve spatial problems:
- Draw Diagrams: When a problem involves specific shapes or spatial relationships, sketching a diagram can provide a clearer understanding. This is especially useful for problems involving angles, parallel lines, or intersecting planes.
- Use Graph Paper: Graph paper can help in maintaining accurate proportions while drawing, making it easier to visualize dimensions and angles precisely. It is particularly helpful when working with coordinate geometry.
- Label Key Points: Once you have drawn your diagram, be sure to label key points, lines, and angles. This will help you stay organized and ensure you don’t miss important details during the solution process.
Leveraging Technology for Visualization
Modern tools can also enhance your ability to visualize complex problems. Various software and online resources offer interactive features that allow you to manipulate geometric shapes, rotate objects, and measure angles. These digital tools provide a dynamic way to explore different scenarios and test out hypotheses without needing to manually draw and measure every time.
Whether using a traditional pencil and paper or utilizing advanced technology, visualizing problems helps you engage with the material more deeply and can significantly improve your problem-solving efficiency. By consistently practicing these techniques, you can develop a stronger spatial awareness that is essential for mastering various mathematical challenges.
How to Check Your Work
Reviewing and verifying your solutions is an essential part of the problem-solving process. By systematically checking your calculations, reasoning, and conclusions, you can ensure that you have arrived at the correct result. This practice helps to catch errors early and reinforces your understanding of the concepts at hand. Here are some effective strategies for checking your work after solving a problem.
Steps for Verifying Your Solutions
Follow these steps to confirm that your solutions are accurate:
- Revisit the Problem Statement: Before double-checking any calculations, make sure you have fully understood the problem. Reread the instructions carefully to confirm that you haven’t missed any important details.
- Check Your Calculations: Go over all the mathematical steps you’ve taken to arrive at your final answer. Pay particular attention to any complex arithmetic or algebraic manipulations to ensure they are correct.
- Assess Your Diagram: If you used a diagram to assist in solving the problem, take another look at it. Check that all labels, angles, and measurements are accurate and consistent with the problem’s requirements.
- Recalculate Using Different Methods: If possible, try to solve the problem using an alternative method or formula. This cross-checking technique can help identify mistakes that might have been overlooked initially.
Using Tools to Verify Results
Many modern tools and resources can assist in verifying your work. Calculators, online solvers, and interactive apps can help you double-check your answers. Additionally, graphing tools can allow you to visually verify your calculations, especially when dealing with coordinates, lines, and angles.
By taking the time to verify each step and using available resources, you can increase your confidence in the accuracy of your solutions and develop a more thorough understanding of the material. Regularly checking your work will also help you recognize any common mistakes you might make and improve your overall problem-solving skills.
Using Geometry Software for Practice
Leveraging technology to enhance your understanding of spatial relationships and mathematical concepts can be highly beneficial. Geometry software allows you to visualize problems in dynamic ways, helping you explore different scenarios and test your understanding in real time. These tools provide an interactive environment where you can manipulate shapes, measure angles, and experiment with various configurations, making learning more engaging and effective.
Benefits of Using Software for Learning
Here are some of the advantages of incorporating software into your study routine:
- Interactive Visualization: Software tools allow you to manipulate objects in real-time, helping you see how changes affect the problem at hand. This can be particularly useful for understanding complex concepts like transformations or symmetry.
- Instant Feedback: Many geometry programs provide immediate feedback, allowing you to test your solutions and correct mistakes on the spot. This instant validation helps reinforce your learning and improves accuracy.
- Multiple Perspectives: With software, you can view the problem from different angles or dimensions, giving you a deeper understanding of the relationships between various elements, such as lines, shapes, and angles.
Popular Geometry Software Tools

Several programs and applications are widely used for studying geometry and other related fields. Some popular ones include:
- GeoGebra: A versatile tool for graphing, geometry, and algebra, GeoGebra allows you to construct, explore, and visualize geometric figures, making it perfect for both beginners and advanced learners.
- Desmos: While primarily known for graphing, Desmos also offers geometric tools that let you create shapes and explore their properties interactively.
- Cabri Geometry: This program focuses on dynamic geometry and is widely used in classrooms to explore geometric constructions and proofs in a highly interactive environment.
By incorporating geometry software into your study habits, you can enhance your problem-solving skills, deepen your understanding, and gain a more intuitive grasp of mathematical concepts. These tools offer a hands-on approach that complements traditional learning, making abstract concepts more tangible and easier to grasp.
Building Confidence in Geometry Tasks
Mastering mathematical challenges often requires more than just understanding concepts; it also involves cultivating the right mindset. Confidence plays a crucial role in how well you tackle problems and progress in your studies. By developing a strong sense of self-assurance in your problem-solving abilities, you can approach each task with clarity and focus, ultimately enhancing both your performance and your overall learning experience.
Steps to Boost Confidence
Here are some effective strategies for building confidence when working through mathematical exercises:
- Start with Basics: Begin by reinforcing foundational concepts. When you are comfortable with basic principles, you are more likely to feel confident when handling more complex problems. Focus on understanding small building blocks before moving to larger, more challenging topics.
- Practice Regularly: The more you practice, the more familiar the problems become. Repetition allows you to become accustomed to different types of tasks, making them easier to solve over time. Consistent practice also helps build fluency and reduces anxiety.
- Break Down Problems: When faced with complex challenges, breaking them down into smaller, more manageable steps can prevent you from feeling overwhelmed. Tackling each step individually allows you to feel more in control and boosts your confidence as you progress.
- Reflect on Mistakes: Mistakes are a natural part of the learning process. Instead of seeing them as failures, view them as opportunities for growth. Take time to analyze what went wrong and learn from it, which will increase your confidence in future tasks.
Mindset Tips for Success
Adopting the right mindset is just as important as applying the correct methods. Here are some mindset shifts to consider:
- Embrace a Growth Mindset: Believe that skills can be developed with effort and persistence. A growth mindset fosters resilience and a willingness to face challenges head-on, rather than avoiding them.
- Stay Positive: Positive reinforcement can work wonders. Celebrate your progress, no matter how small, and maintain an optimistic attitude about your abilities. This positive outlook helps you stay motivated even when faced with difficulties.
- Visualize Success: Before attempting a task, take a moment to mentally visualize yourself solving the problem. This mental rehearsal can increase your confidence and make the process feel less intimidating.
By implementing these strategies, you can steadily build confidence in tackling mathematical challenges. As your self-assurance grows, so will your ability to approach tasks with clarity and achieve greater success.
Essential Geometry Resources for Students
To succeed in mathematical subjects that involve shapes, angles, and spatial reasoning, having the right resources is essential. These resources not only support understanding complex topics but also offer practical tools for solving problems more efficiently. Whether through textbooks, online tools, or peer collaborations, having access to a variety of learning aids can make a significant difference in mastering the subject.
Books and Textbooks
Textbooks remain one of the most reliable resources for students to learn foundational concepts. They provide clear explanations, step-by-step examples, and practice exercises. A good textbook covers everything from the basics to advanced topics, allowing students to learn at their own pace.
- High-Quality Textbooks: Look for textbooks recommended by your curriculum or academic institution, as they are likely to provide a structured approach to the subject.
- Reference Books: These often provide deeper insights and additional examples that can help clarify complex concepts and offer alternative approaches to solving problems.
Online Tools and Apps
The digital age has opened up a vast array of online tools and apps designed to aid in the learning process. These platforms often provide interactive lessons, video tutorials, and instant feedback, making them a great addition to traditional learning methods.
- Interactive Websites: Websites like Khan Academy, Coursera, or specific math learning sites offer free resources such as instructional videos, quizzes, and practice exercises.
- Mathematical Software: Software like GeoGebra and Desmos allows students to visualize geometric shapes and explore various mathematical concepts in a hands-on way.
- Calculator Apps: Mobile apps such as Wolfram Alpha provide powerful computational tools to solve equations and perform step-by-step calculations.
By leveraging these resources, students can strengthen their understanding, practice problem-solving skills, and develop the confidence needed to succeed in their studies. Combining traditional learning with digital tools creates a well-rounded approach that can make mastering the subject more engaging and effective.
Preparing for Exams with Practice B
Effective preparation for mathematical assessments requires a combination of understanding core concepts, practicing problem-solving techniques, and refining skills through consistent exercises. Focusing on problem sets that challenge your knowledge helps reinforce learning and boosts confidence. By engaging with various types of questions, students can strengthen their ability to tackle complex problems under exam conditions.
One of the most efficient ways to prepare is by working through sets of exercises that mimic exam-style questions. These sets not only help in recalling learned concepts but also provide insight into the types of problems you may encounter. Practicing in this way allows you to identify areas of weakness and focus your efforts where they are needed most.
- Review Key Concepts: Begin by revisiting the fundamental principles that will be tested. Ensure a solid grasp of the rules, formulas, and theorems that form the foundation of the subject.
- Simulate Exam Conditions: Set aside time to work on exercises under timed conditions. This will help you manage your time effectively during the actual exam and build confidence in your ability to think and solve problems quickly.
- Analyze Mistakes: When reviewing your work, focus on understanding the errors you made. This can reveal gaps in your knowledge and provide a clearer path to improvement.
By consistently engaging with exercises that mirror the structure and difficulty of your upcoming assessments, you’ll be better prepared for any challenges the exam may present. Regular practice also allows for a deeper understanding of how to approach different problem types and how to apply concepts effectively in varied contexts.