
Preparing for a challenging math test requires a deep understanding of key concepts and the ability to apply them accurately. Focused practice is essential for mastering the different techniques used to solve complex problems. With the right strategies and a solid grasp of mathematical principles, students can approach assessments with confidence.
Reviewing core principles is the first step towards performing well. It’s not just about memorizing formulas; it’s about knowing how to apply them in various contexts. Developing a clear understanding of mathematical relationships is crucial for solving problems efficiently.
Another vital component of preparation is strategic problem-solving. Regular practice with progressively challenging questions builds both skill and confidence. By simulating real test conditions and focusing on areas of weakness, you can maximize your chances of success.
Trigonometry Final Exam Overview
As you approach the culmination of your studies in advanced mathematics, it’s essential to grasp the overall structure and expectations of the assessment. This section provides an overview of the key areas that will be tested, offering insight into the types of problems you will encounter. A solid understanding of these concepts will help guide your preparation and increase your confidence.
Math assessments of this level often cover a broad spectrum of topics, challenging students to apply their knowledge in a variety of ways. The questions typically vary in difficulty, from straightforward calculations to more complex problem-solving scenarios. A comprehensive review of each topic is necessary to perform well under test conditions.
| Topic | Description | Importance |
|---|---|---|
| Angles and Their Measures | Understanding how to work with different angle types and units. | High |
| Functions and Identities | Familiarity with sine, cosine, tangent, and their identities. | High |
| Graphing Techniques | Being able to plot and analyze functions on a coordinate plane. | Medium |
| Solving Equations | Solving for unknowns using various mathematical methods. | High |
| Applications | Applying principles to solve real-world problems. | Medium |
Key Topics to Review for Trigonometry
When preparing for an assessment in advanced mathematics, it’s essential to focus on the core concepts that are most likely to appear. These topics form the foundation of the subject and are crucial for solving problems efficiently. A well-rounded review will ensure that you are well-prepared to tackle the variety of questions that may arise.
Understanding the relationships between angles and their corresponding functions is fundamental. You should be comfortable working with the basic trigonometric functions and their identities. This knowledge will allow you to manipulate and solve equations effectively.
Additionally, being proficient in graphing and interpreting functions on a coordinate plane is important for visualizing solutions. Knowing how to apply formulas and recognize patterns can make complex problems more manageable.
Finally, don’t overlook the importance of problem-solving strategies. Practice with word problems and real-world applications will improve your ability to translate theoretical knowledge into practical solutions under time constraints.
Essential Formulas for Trigonometry Exams
In preparation for a challenging mathematics test, mastering key equations is crucial. These formulas serve as the foundation for solving a wide range of problems, from basic calculations to more complex applications. By reviewing and understanding these formulas, you’ll be able to tackle problems with greater ease and precision.
Key Mathematical Identities
Several identities are fundamental to solving various types of problems. Here are some of the most essential ones to remember:
- Pythagorean Identity: ( sin^2(theta) + cos^2(theta) = 1 )
- Sum and Difference Formulas:
- ( sin(A pm B) = sin(A)cos(B) pm cos(A)sin(B) )
- ( cos(A pm B) = cos(A)cos(B) mp sin(A)sin(B) )
- Double Angle Formulas:
- ( sin(2A) = 2sin(A)cos(A) )
- ( cos(2A) = cos^2(A) – sin^2(A) )
Useful Conversion Formulas
Understanding how to convert between different units and measurements is essential for solving problems efficiently. Here are a few key conversion formulas:
- Angle Conversion: ( text{Degrees} = text{Radians} times frac{180}{pi} )
- Area of a Triangle: ( A = frac{1}{2}ab sin(C) ), where (a) and (b) are sides and (C) is the included angle.
- Law of Sines: ( frac{sin(A)}{a} = frac{sin(B)}{b} = frac{sin(C)}{c} )
By familiarizing yourself with these key formulas, you’ll be well-equipped to handle a variety of mathematical problems during your assessment. Practicing their application will help reinforce your understanding and improve your problem-solving speed.
Understanding Trigonometric Ratios and Functions
At the heart of many mathematical problems lies the understanding of ratios and their corresponding functions. These relationships describe how angles and side lengths in right-angled triangles are connected. Mastering these ratios is essential for solving a wide variety of problems, from basic calculations to more complex applications in different fields of study.
The Core Ratios
In any right-angled triangle, three primary ratios are used to relate the angles and sides. These are known as the sine, cosine, and tangent ratios. Each ratio compares two sides of a triangle, making it easier to find unknown values based on given information.
- Sine: ( sin(theta) = frac{text{Opposite}}{text{Hypotenuse}} )
- Cosine: ( cos(theta) = frac{text{Adjacent}}{text{Hypotenuse}} )
- Tangent: ( tan(theta) = frac{text{Opposite}}{text{Adjacent}} )
Using These Functions
Beyond the basic ratios, these functions can also be extended to all angles through the unit circle. By understanding how sine, cosine, and tangent behave for angles greater than 90°, you can solve more complex problems involving angles and functions in a variety of contexts.
- Unit Circle: The unit circle allows for the extension of trigonometric ratios to all angles, providing a way to visualize these functions as they repeat periodically.
- Graphs of Functions: The graphical representation of these ratios helps identify patterns and provides a visual method for solving problems.
By thoroughly understanding these fundamental ratios and their functions, you’ll be well-prepared to handle various mathematical challenges. This knowledge serves as the foundation for more advanced topics and real-world applications.
Common Trigonometry Mistakes to Avoid
When solving problems in advanced mathematics, small errors can have a big impact on the final result. Understanding the common pitfalls will help you approach problems with greater care and accuracy. By recognizing and avoiding these frequent mistakes, you can improve your problem-solving skills and avoid unnecessary setbacks.
Some of the most common errors occur when dealing with angle measures, identities, and calculations. These mistakes are often a result of misunderstanding key concepts or overlooking important steps in the solution process. Here are a few critical mistakes to watch out for:
| Mistake | Explanation | How to Avoid |
|---|---|---|
| Confusing Radians and Degrees | Using the wrong unit when working with angles can lead to incorrect results. | Always ensure you’re working in the correct unit, and convert between radians and degrees when necessary. |
| Incorrect Use of Identities | Misapplying or forgetting basic identities like the Pythagorean identity can cause errors in solving equations. | Review and memorize key identities, and double-check their application in your solutions. |
| Forgetting to Apply the Unit Circle | Not considering the unit circle can lead to mistakes when extending functions to angles beyond 90°. | Understand the periodic nature of these functions and use the unit circle for reference when needed. |
| Misinterpreting Word Problems | Failing to translate word problems into mathematical expressions correctly can result in wrong answers. | Carefully read the problem and identify key information such as angle measures and side lengths. |
| Rounding Too Early | Rounding off intermediate steps may lead to inaccurate final results. | Avoid rounding until the final step of the calculation to maintain precision. |
By being mindful of these common mistakes and taking extra care when working through problems, you can avoid errors and improve your performance. Practice and attention to detail are key to mastering this subject and achieving success in assessments.
How to Solve Trigonometric Equations
Solving equations that involve angles and their corresponding functions is a key skill in advanced mathematics. These equations often require applying specific techniques to isolate the variable and find the solution. Understanding the basic principles and strategies will enable you to approach these problems confidently and accurately.
Steps for Solving Equations
To solve any equation involving trigonometric functions, it’s essential to follow a systematic approach. Below are the general steps to keep in mind:
- Identify the Type of Equation: Determine whether you are working with basic or more complex functions, such as sine, cosine, or tangent.
- Isolate the Function: Rearrange the equation so that the trigonometric function is on one side, making it easier to solve.
- Use Inverse Functions: If necessary, apply inverse functions to find the angle that corresponds to the value of the trigonometric function.
- Consider Multiple Solutions: Some equations may have more than one solution due to the periodic nature of trigonometric functions.
Example of Solving an Equation
Let’s take an example to demonstrate the process. Consider the equation:
| Equation | Steps | Solution |
|---|---|---|
| ( sin(x) = 0.5 ) | 1. Isolate the function: Already isolated. 2. Apply inverse sine: ( x = sin^{-1}(0.5) ) 3. Consider all possible angles based on the periodic nature of sine. |
Solution: ( x = 30^circ, 150^circ ) (in degrees), or ( x = frac{pi}{6}, frac{5pi}{6} ) (in radians). |
By following these steps and practicing with various examples, you will become proficient in solving these types of equations. It’s important to remember that the periodic nature of the functions often leads to multiple solutions within a given interval, so always consider all possibilities when solving equations.
Preparing for Word Problems in Trigonometry
Word problems often present unique challenges, as they require translating real-world scenarios into mathematical equations. These problems can involve various mathematical functions and require a strong understanding of relationships between angles, distances, and other elements. Developing a methodical approach to solving word problems will help you break down complex situations into solvable parts.
Steps to Approach Word Problems
When faced with a word problem, it’s important to follow a structured process to ensure that all elements are accounted for and that you approach the problem logically. Here are the steps to keep in mind:
- Read Carefully: Identify key information such as angles, side lengths, and the question being asked. Pay attention to units of measurement.
- Draw a Diagram: Visualizing the problem can make it easier to understand and organize the given information.
- Set Up the Equation: Use the appropriate mathematical functions or identities based on the relationships in the problem. Often, this will involve sine, cosine, or tangent.
- Solve and Interpret: Solve the equation, and then interpret the result in the context of the problem.
Example of a Word Problem
Let’s take a look at a typical scenario to apply these steps:
| Problem | Steps | Solution |
|---|---|---|
| A ladder leans against a wall. The angle between the ground and the ladder is 30 degrees, and the ladder is 10 feet long. How high does the top of the ladder reach? | 1. Draw a right triangle with the ladder as the hypotenuse. 2. Use the sine function to find the height: ( sin(30^circ) = frac{h}{10} ). 3. Solve for h: ( h = 10 times sin(30^circ) ). |
Solution: ( h = 5 ) feet. The top of the ladder reaches 5 feet above the ground. |
By following these steps and practicing with a variety of word problems, you will improve your ability to quickly translate real-world scenarios into mathematical solutions. The key is to stay organized, use diagrams, and apply the correct functions based on the given information.
Understanding Angles and Their Measures
Angles are fundamental elements in various mathematical concepts and problem-solving scenarios. Whether you are working with geometric shapes, vectors, or periodic functions, understanding how to measure and work with angles is essential. Proper knowledge of angle units and their relationships enables you to approach more complex topics with confidence and precision.
Types of Angle Measures
Angles can be measured in two main units: degrees and radians. Each unit has its advantages, and it’s crucial to understand when and how to use them. Here’s a brief overview of both:
- Degrees: This is the most commonly used unit for measuring angles, where one full rotation around a point is 360°. It’s often used in everyday situations and basic geometry.
- Radians: This unit is widely used in higher-level mathematics, where one full rotation corresponds to (2pi) radians. It is preferred in calculus and functions involving periodicity.
Converting Between Degrees and Radians
Understanding how to convert between these two units is an important skill. To convert from degrees to radians, multiply by (frac{pi}{180}). To convert from radians to degrees, multiply by (frac{180}{pi}). Here’s an example:
| Conversion | Formula | Example |
|---|---|---|
| Degrees to Radians | ( text{Degrees} times frac{pi}{180} ) | 45° = ( 45 times frac{pi}{180} = frac{pi}{4} ) radians |
| Radians to Degrees | ( text{Radians} times frac{180}{pi} ) | ( frac{pi}{3} ) radians = ( frac{pi}{3} times frac{180}{pi} = 60^circ ) |
Mastering these conversions will allow you to navigate problems seamlessly, regardless of the angle unit used. Whether you are working with degrees or radians, a strong understanding of these concepts forms the foundation for solving more advanced mathematical problems.
Graphs and Their Properties
Understanding the behavior of periodic functions is essential for analyzing and solving various mathematical problems. The graphs of these functions exhibit recurring patterns that help visualize the relationships between the input and output values. By studying their key properties, such as amplitude, period, and shifts, one can easily predict and interpret the graph’s behavior under different conditions.
Key Features of Periodic Graphs
When exploring the graphs of common periodic functions, there are several key features to pay attention to. These properties define the function’s shape and determine how it behaves over time. The primary aspects include the amplitude, period, phase shift, and vertical shift. Let’s break them down:
- Amplitude: The height of the graph from its center line to the highest or lowest point. It determines how far the function deviates from the midline.
- Period: The length of one complete cycle of the function. It represents how often the pattern repeats itself along the horizontal axis.
- Phase Shift: A horizontal displacement of the graph, shifting it left or right along the x-axis.
- Vertical Shift: Moves the entire graph up or down along the y-axis, changing the position of the midline.
Graphing the Sine Function
Let’s consider a basic example of the sine function, ( y = sin(x) ). The standard sine wave has an amplitude of 1, a period of ( 2pi ), and its midline is at y = 0. When transformations are applied to the sine function, such as changes to its amplitude, period, or shifts, the appearance of the graph changes accordingly. Below is a table illustrating these transformations:
| Transformation | New Function | Effect on the Graph |
|---|---|---|
| Amplitude Change | y = 2sin(x) | The amplitude increases, making the graph taller. |
| Period Change | y = sin(2x) | The period decreases, causing the graph to repeat more frequently. |
| Phase Shift | y = sin(x – frac{pi}{2}) | The graph shifts to the right by ( frac{pi}{2} ) units. |
| Vertical Shift | y = sin(x) + 3 | The entire graph shifts up by 3 units. |
By mastering these properties and transformations, you can better understand how functions behave and how their graphs are affected by changes to the equation. This understanding allows you to approach mathematical problems with greater confidence and accuracy.
Using the Unit Circle for Solutions
The unit circle is a fundamental tool for solving various mathematical problems involving angles and periodic functions. It provides a visual way to understand the relationships between angles and the coordinates of points on a circle. By using the unit circle, one can easily find values for sine, cosine, and other related functions, as well as solve equations that involve these functions.
One of the primary advantages of the unit circle is that it enables you to find exact values for the trigonometric functions of key angles, such as ( 0^circ ), ( 30^circ ), ( 45^circ ), ( 60^circ ), and ( 90^circ ). These values are critical when working through mathematical problems and verifying solutions.
Understanding the Unit Circle
The unit circle is a circle with a radius of 1, centered at the origin of a coordinate plane. The coordinates of any point on the unit circle correspond to the cosine and sine values for the angle formed by the radius and the positive x-axis. These coordinates are written as ( (cos(theta), sin(theta)) ), where ( theta ) is the angle in standard position.
Key Angles and Their Values
To simplify calculations, here are some common angles and their corresponding sine and cosine values on the unit circle:
| Angle (θ) | Sine (sin θ) | Cosine (cos θ) |
|---|---|---|
| 0° | 0 | 1 |
| 30° (π/6) | 1/2 | √3/2 |
| 45° (π/4) | √2/2 | √2/2 |
| 60° (π/3) | √3/2 | 1/2 |
| 90° (π/2) | 1 | 0 |
Using the Unit Circle for Solving Equations
To solve equations involving sine, cosine, or other trigonometric functions, the unit circle can be incredibly useful. For example, when solving for the sine or cosine of an angle, you can refer to the unit circle to quickly find the values. Additionally, the unit circle can be used to determine the values of other functions like tangent or secant by applying basic identities.
- Start by identifying the angle for which you need to find the value.
- Locate this angle on the unit circle, noting its coordinates.
- The x-coordinate gives you the cosine, and the y-coordinate gives you the sine.
- Use these values to solve your equation or verify the solution.
By practicing these techniques, you can efficiently solve a wide variety of problems that involve periodic functions and angles. The unit circle is a powerful tool that not only simplifies calculations but also provides deeper insights into the behavior of these functions across different domains.
Inverse Trigonometric Functions Explained
Inverse functions play a crucial role in solving equations that involve angles. They are used to find the angle corresponding to a given value of a trigonometric function. Essentially, inverse functions allow you to reverse the process of determining a trigonometric ratio and solve for the angle itself. These functions are particularly useful when working with problems involving unknown angles or when trying to express solutions in terms of specific angle measures.
Inverse functions for sine, cosine, tangent, and other related functions are denoted with a superscript “-1” (e.g., ( sin^{-1} ), ( cos^{-1} ), ( tan^{-1} )). Despite the notation, these are not exponents but represent inverse operations. Below, we explore how to use these functions and understand their properties.
Key Inverse Functions and Their Uses
The most commonly used inverse functions are the inverse sine, cosine, and tangent. Each of these functions takes a value from the range of the corresponding trigonometric function and returns the angle for which the trigonometric function would yield that value. Here are the primary inverse functions:
- Inverse Sine (sin⁻¹): Finds the angle whose sine is a given number. The output is typically restricted to angles between ( -90^circ ) and ( 90^circ ).
- Inverse Cosine (cos⁻¹): Determines the angle whose cosine is a given value. The range of this function is between ( 0^circ ) and ( 180^circ ).
- Inverse Tangent (tan⁻¹): Returns the angle whose tangent equals a specified number. This function produces results between ( -90^circ ) and ( 90^circ ).
How to Use Inverse Functions
To use these inverse functions, you need to follow specific steps depending on the type of function you are working with. Here’s a general process for solving problems involving inverse trigonometric functions:
- Identify the trigonometric ratio: Start by recognizing which ratio is given, whether it’s sine, cosine, or tangent.
- Apply the inverse function: Use the appropriate inverse function to solve for the angle. For example, if you’re given the sine of an angle, you would apply the inverse sine function to find the angle.
- Check the range: Ensure that the solution falls within the valid range of the inverse function. For instance, the result of ( sin^{-1} ) will always be between ( -90^circ ) and ( 90^circ ), so you may need to adjust the solution accordingly if the value is outside of this range.
- Express the solution: Finally, write the angle as the solution to the problem, ensuring it matches the expected units (degrees or radians).
By practicing these steps, you can effectively solve problems involving angles and trigonometric functions, ensuring that you can find the correct angle even when the trigonometric ratio is known.
Applying Pythagorean Theorem in Trigonometry
The Pythagorean theorem is one of the most fundamental principles in geometry and plays a significant role in solving problems related to angles and side lengths in right triangles. It states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. This relationship provides a foundation for various calculations involving trigonometric functions and is essential for understanding how angles and sides relate in these contexts.
By using the Pythagorean theorem, you can derive critical trigonometric identities and solve for unknown side lengths or angles in right triangles. This principle not only supports the basic understanding of geometric relationships but also serves as a tool for solving more complex problems in various applications, from engineering to physics.
How the Pythagorean Theorem Relates to Trigonometric Functions
The Pythagorean theorem is closely tied to the definitions of the fundamental trigonometric functions: sine, cosine, and tangent. It helps establish key relationships between the sides of a right triangle, which are essential when solving for these functions. Here’s how the theorem connects with trigonometric ratios:
- Sine (sin): The sine of an angle is the ratio of the opposite side to the hypotenuse. Using the Pythagorean theorem, if you know the lengths of the adjacent side and the hypotenuse, you can calculate the opposite side.
- Cosine (cos): The cosine of an angle is the ratio of the adjacent side to the hypotenuse. With the Pythagorean theorem, if the opposite side and hypotenuse are known, you can determine the length of the adjacent side.
- Tangent (tan): The tangent of an angle is the ratio of the opposite side to the adjacent side. The Pythagorean theorem can be used to find one of these sides if the other two are known.
Using the Pythagorean Theorem to Solve Problems
In many cases, the Pythagorean theorem is a starting point for solving right triangle problems. When given two side lengths, you can use the theorem to find the third side, which is often necessary to compute trigonometric values. The formula for the theorem is:
a² + b² = c², where a and b are the lengths of the two legs of the right triangle, and c is the length of the hypotenuse.
Here’s a step-by-step process to apply the Pythagorean theorem in a problem:
- Identify the sides: Label the sides of the triangle. The hypotenuse is always the longest side, opposite the right angle.
- Apply the theorem: If two sides are known, substitute those values into the formula.
- Solve for the unknown: Rearrange the formula to solve for the missing side length.
- Use the result: Once the missing side is found, use it to calculate the desired trigonometric ratio.
By applying this method, you can effectively solve for unknown sides and angles, providing a deeper understanding of the relationships within right triangles and making it easier to solve more complex problems involving angles and distances.
Strategies for Time Management During Exams
Efficient time management is crucial when facing an assessment, especially when the questions require complex problem-solving. One of the biggest challenges during an assessment is balancing the time spent on each question while ensuring accuracy. To maximize performance, it’s important to have a clear plan for how to approach the test and allocate your time wisely.
By using effective strategies, you can stay organized, reduce stress, and ensure that you complete all the questions within the allotted time. A well-thought-out approach can make a significant difference in how well you perform, allowing you to focus on your strengths and avoid unnecessary pressure during the process.
Planning Your Time: Prioritize and Pace Yourself
The key to managing time effectively during an assessment is planning. Here are some strategies to consider:
- Read the instructions carefully: Before starting, take a few minutes to read through the entire assessment. Understanding the structure of the test will help you decide how much time to spend on each section.
- Estimate the time for each section: Divide the total time by the number of sections or questions. For more difficult sections, allow a little extra time, but ensure you don’t spend too much on any one task.
- Start with what you know: Begin by answering the questions that you are most confident about. This boosts your morale and ensures that you’re accumulating points early on.
How to Avoid Time Draining Pitfalls
Time management isn’t just about allocating time to questions–it’s also about avoiding distractions and preventing unnecessary delays:
- Don’t get stuck on tough questions: If a question is taking too long, move on and come back to it later. Spending excessive time on one problem can reduce your chances of completing the entire assessment.
- Keep track of time: Use a watch or the clock to monitor your progress. Set milestones to make sure you’re on schedule, and adjust your pace if necessary.
- Leave time for review: If possible, save the last few minutes to review your answers. Double-check for any mistakes, especially on questions that required detailed calculations or multiple steps.
By managing your time effectively, you will not only ensure that you complete all the questions, but you will also reduce anxiety and improve your performance. The right approach will help you stay calm, organized, and confident throughout the assessment.
How to Check Your Trigonometry Answers
Verifying your solutions is a critical step in ensuring accuracy before finalizing your work. Even if you feel confident in your calculations, it’s important to review each step carefully. By double-checking your results, you can catch small mistakes and avoid losing unnecessary points.
Effective checking involves more than simply glancing at your work. A thorough review requires looking for errors in your reasoning, re-evaluating your methods, and testing your results to ensure they make sense within the context of the problem.
Step-by-Step Review Process
When reviewing your solutions, follow a systematic approach:
- Revisit each step: Go back through the steps of your solution, starting from the beginning. Confirm that each transition between steps is logical and based on solid reasoning.
- Check for common calculation mistakes: Look for errors in basic arithmetic, signs, or misplacement of decimals. These small mistakes can sometimes lead to large errors in the final result.
- Recalculate using an alternative method: If possible, solve the problem using a different approach. This can help confirm your original result and highlight any inconsistencies.
Testing the Solution
Once you’ve reviewed your steps, test your final solution to make sure it’s reasonable:
- Estimate the expected range: For problems involving angles or ratios, consider whether your result falls within a reasonable range. For example, a sine or cosine value should always lie between -1 and 1.
- Use inverse operations: Apply inverse functions to check whether they lead back to the original values or conditions. If they do, your solution is likely correct.
- Cross-check with a calculator: If available, use a scientific calculator or software tool to verify your numerical results. This can help confirm the precision of your calculations.
By carefully reviewing your work and testing your solutions, you increase the likelihood of catching errors before submitting your work. A diligent review process not only boosts your confidence but also ensures that your results are as accurate as possible.
Mock Exams and Practice Problems
One of the most effective ways to prepare for any test is by practicing under conditions that closely resemble the actual assessment. Simulating real test scenarios through mock exercises and practice problems helps familiarize you with the format, timing, and types of questions you may encounter. This method not only builds confidence but also identifies areas where further improvement is needed.
By working through sample problems, you can refine your problem-solving skills, improve your speed, and identify any gaps in knowledge. It’s important to challenge yourself with problems that cover a broad range of topics to ensure comprehensive preparation.
Benefits of Mock Assessments
- Time management practice: Working on timed practice tests teaches you how to allocate time effectively and avoid spending too long on any one question.
- Stress reduction: Simulating the test environment reduces anxiety on the actual day. The more you practice, the more comfortable you become with the pressure.
- Identify weak spots: Mock exercises highlight areas where you may struggle, allowing you to focus your revision efforts on those specific topics.
Effective Use of Practice Problems
When using practice problems to study, consider these strategies:
- Start simple: Begin with basic questions to build a strong foundation before moving on to more complex problems.
- Simulate real conditions: Complete practice tests in a quiet environment with no distractions, and stick to the allotted time limit.
- Review mistakes: After completing a practice set, go over any mistakes you made and ensure you understand where you went wrong. This helps avoid similar errors in the future.
Incorporating mock exams and practice problems into your study routine can significantly boost your preparedness, enhance your test-taking abilities, and increase your chances of success.
Tips for Success on Trigonometry Exams
Achieving success in mathematics assessments requires more than just understanding the material. Effective preparation, smart strategies, and a positive mindset all play vital roles in performing well. By adopting a few key practices and techniques, you can enhance your performance and tackle challenges confidently.
Preparation Strategies
- Master the fundamentals: Ensure that you have a strong grasp of the basic concepts, as these will form the foundation for solving more complex problems.
- Practice regularly: Consistent practice helps reinforce key ideas and increases problem-solving speed. Use a variety of resources, including textbooks, online platforms, and past papers.
- Break down complex problems: Break each question into smaller, more manageable parts. Focus on understanding each step to avoid getting overwhelmed.
During the Test
- Read each question carefully: Take your time to understand exactly what is being asked. Pay attention to keywords, such as “find,” “calculate,” or “prove,” which guide your approach.
- Manage your time: Allocate time wisely for each question. If you get stuck, move on and return to the difficult problem later to avoid wasting time.
- Double-check your work: After completing the test, review your answers carefully. Ensure that you haven’t made simple mistakes and that all steps are logically consistent.
Mindset for Success
- Stay calm and focused: Anxiety can impair your ability to think clearly. Take deep breaths and approach each problem methodically.
- Stay positive: Keep a positive attitude throughout your preparation and during the test. Confidence can improve your problem-solving ability.
- Learn from mistakes: If you make a mistake, don’t be discouraged. Mistakes are an opportunity to learn and improve for the next time.
By following these strategies, you can enhance your chances of success. Remember, preparation is key, and a calm, focused mindset will help you tackle any challenges that come your way.
Resources for Further Study in Trigonometry
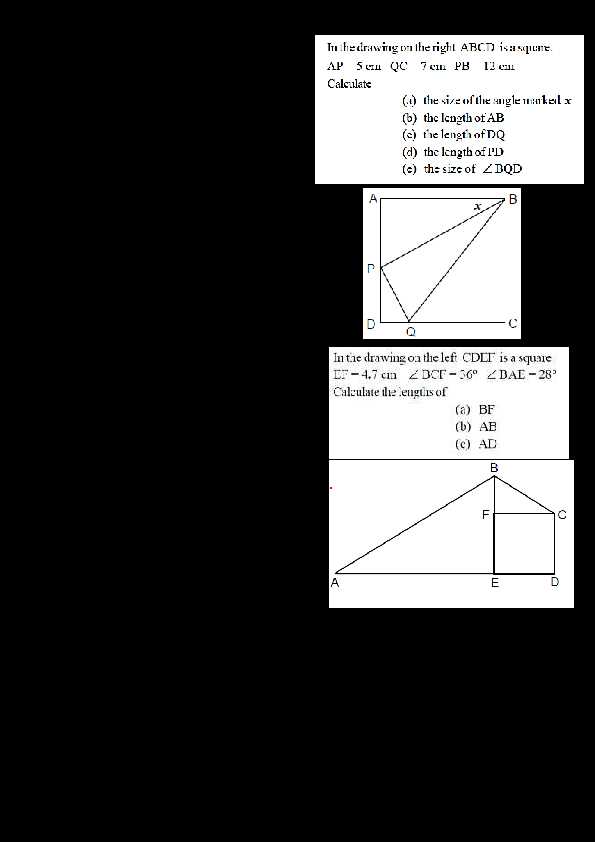
Expanding your knowledge and understanding of mathematical concepts requires continuous learning and access to various resources. Whether you are looking to deepen your understanding or improve specific skills, there are numerous tools available that can help you build a stronger foundation and gain mastery over the subject. Below are some recommended materials and platforms to aid in further study.
Books and Textbooks
- Mathematical Methods for Beginners: A great starting point for building a solid foundation in basic mathematical concepts.
- Advanced Problem-Solving Guides: Books that focus on problem-solving techniques and offer detailed solutions to challenging questions.
- Reference Texts: Authoritative resources that delve deep into mathematical theory, providing comprehensive explanations and examples.
Online Learning Platforms
- Khan Academy: Offers free lessons on various mathematical topics, including video tutorials and practice exercises.
- Coursera: Provides online courses taught by professors from top universities. These courses often cover more advanced topics in mathematics.
- edX: A platform for online courses that offers many options related to mathematics and related subjects, often in collaboration with top institutions.
Interactive Tools and Apps
- GeoGebra: A dynamic mathematics software that allows you to visualize and explore mathematical concepts interactively.
- Wolfram Alpha: An online computational tool that can help solve problems, generate plots, and provide step-by-step solutions.
- Desmos: A graphing calculator that lets you explore mathematical concepts visually, ideal for understanding complex functions.
Practice Problems and Worksheets
- Online Problem Sets: Websites offering downloadable worksheets and problem sets that provide an opportunity for self-assessment and practice.
- Math Stack Exchange: A community-driven platform where you can ask questions and find solutions to challenging problems.
- Interactive Quizzes: Many online resources offer quizzes designed to test your knowledge and help reinforce learning.
Using a combination of these resources, you can explore the subject from different perspectives, improving both your theoretical understanding and practical problem-solving skills. Consistent study, along with a variety of learning tools, will ensure progress and mastery over time.