
Preparing for a challenging academic test requires a solid understanding of core concepts and effective strategies to apply your knowledge. In this section, we’ll cover essential topics and methods to ensure you feel confident when facing your upcoming evaluation.
Mastering key principles is crucial to tackling complex questions, and practicing specific skills will help reinforce your learning. Whether it’s understanding data analysis or applying formulas, mastering the fundamentals will significantly boost your performance.
We’ll also focus on common pitfalls students encounter and provide actionable tips to avoid them. A structured approach will guide you through various types of problems, helping you improve both accuracy and speed during your test.
Comprehensive Guide to Mastering Your Assessment
This section will help you prepare for your upcoming test by exploring important topics and offering clear solutions to common problems. You’ll learn to recognize patterns in questions and develop a systematic approach for tackling different types of tasks effectively.
Key Concepts to Focus On
To perform well, it’s essential to understand and apply the following principles:
- Data interpretation and analysis
- Calculation techniques and their real-world applications
- Formulas and when to use them correctly
- Identifying errors and correcting misinterpretations
Problem-Solving Strategies
Having a structured approach to problem-solving is crucial. Follow these steps to improve your chances of success:
- Identify the key components of the problem.
- Decide which technique or formula is needed.
- Break the problem down into smaller, manageable parts.
- Check your work for accuracy at each stage.
By practicing these strategies and reviewing sample questions, you’ll gain confidence in handling a wide range of topics on test day.
Key Topics to Focus On
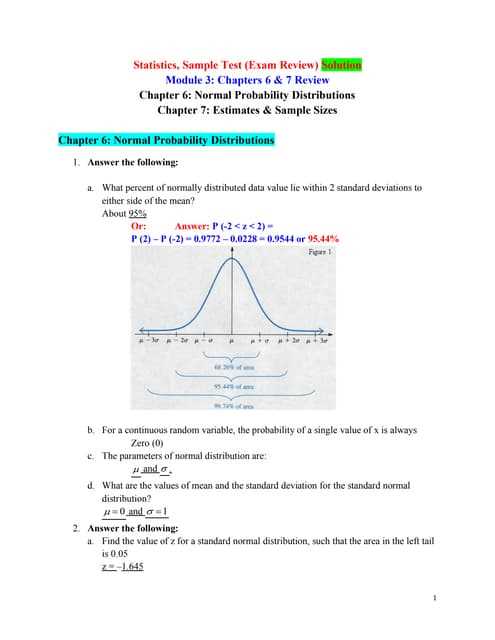
Focusing on the right areas of study can significantly improve your performance. Identifying core concepts and mastering their application will help you solve problems efficiently and confidently. In this section, we will highlight the most important topics you should prioritize as you prepare.
Essential Mathematical Techniques
Understanding the fundamental methods is crucial to tackling complex problems. Pay attention to the following:
- Calculating mean, median, and mode
- Working with standard deviation and variance
- Applying probability distributions
- Mastering correlation and regression analysis
Practical Problem-Solving Skills
Being able to analyze and solve problems effectively is just as important as knowing the theory. Focus on:
- Interpreting data sets and drawing conclusions
- Recognizing patterns in word problems
- Utilizing formulas for different scenarios
- Identifying common errors and avoiding them
Understanding Probability for Your Assessment
Probability plays a key role in many questions, helping to assess outcomes based on known conditions. Mastering this concept is essential for approaching questions that involve uncertain events and predictions. By understanding how probability works, you will be able to calculate the likelihood of different scenarios and make informed decisions in solving problems.
Focus on grasping the basic principles, such as the difference between independent and dependent events, as well as how to apply probability rules to real-life situations. Knowing how to calculate probabilities using combinations, permutations, and various distribution models will give you a strong foundation for handling more advanced problems during your test.
Essential Formulas to Remember
Having a solid understanding of key mathematical formulas is crucial for efficiently solving a wide range of problems. These formulas provide the foundation for calculations and analysis, ensuring that you can approach tasks methodically and accurately. Below are some of the most important equations you should familiarize yourself with.
| Formula | Description |
|---|---|
| Mean = (Sum of all values) / n | Used to calculate the average of a data set. |
| Variance = Σ(x – mean)² / n | Measures how spread out the data points are from the mean. |
| Standard Deviation = √Variance | Indicates the average deviation of data points from the mean. |
| P(A and B) = P(A) * P(B) | Formula for independent events in probability. |
| P(A or B) = P(A) + P(B) – P(A and B) | Formula for calculating the probability of either event A or B happening. |
By memorizing these formulas and understanding how to apply them in different contexts, you’ll be well-equipped to tackle a variety of questions efficiently.
Common Mistakes to Avoid
When working through complex problems, it’s easy to make mistakes that can lead to incorrect results. These errors often stem from misunderstandings of key concepts or careless application of methods. Recognizing common pitfalls will help you avoid them and approach questions more confidently.
Calculation Errors
One of the most frequent mistakes occurs during the calculation process. These include:
- Misapplying formulas or using incorrect variables
- Forgetting to square terms when calculating variance
- Incorrectly simplifying complex expressions
Misinterpreting Data
Another common issue arises from incorrect interpretation of data or results. Avoid these errors:
- Assuming causality when only correlation is present
- Ignoring outliers that may skew results
- Misunderstanding the context of probability questions
By staying mindful of these common mistakes and applying a systematic approach to each problem, you can improve both accuracy and efficiency in your work.
How to Analyze Data Efficiently

Efficient data analysis involves organizing information, identifying patterns, and drawing conclusions based on evidence. A structured approach is essential for extracting meaningful insights and avoiding unnecessary confusion. This section covers key steps to help you analyze data quickly and accurately.
Steps to Analyze Data Effectively
Follow these steps to streamline your analysis process:
- Gather all relevant data and organize it logically
- Identify the key variables and their relationships
- Use visual tools such as graphs and charts to detect trends
- Apply appropriate methods to summarize and describe the data
- Interpret the results in the context of the problem at hand
Common Tools for Data Analysis
Several tools and techniques can enhance your ability to analyze data:
- Descriptive statistics (mean, median, mode) for summarizing data
- Graphical representations (bar charts, histograms) for visualization
- Statistical tests to validate hypotheses and determine significance
By following a systematic process and utilizing the right tools, you can efficiently analyze data and make informed decisions.
Important Concepts Explained
Understanding the core ideas behind mathematical analysis is essential for solving complex problems effectively. These concepts provide the foundation for interpreting data, making predictions, and drawing conclusions. In this section, we will break down some of the most important principles that you need to grasp for success.
Understanding Probability and Distribution
One key area of focus is the likelihood of events occurring and how to model them. Probability helps you assess risks and outcomes based on available data. Common distributions such as normal and binomial play an essential role in predicting future events.
- Probability of events (independent vs. dependent)
- Normal distribution and its significance in modeling
- Binomial distribution for discrete outcomes
Correlation and Causation
Another critical concept is the relationship between two variables. While correlation shows how variables move together, causation indicates a direct cause-effect relationship. Understanding the difference is crucial to avoid drawing false conclusions.
- Correlation coefficient and its interpretation
- Identifying potential causal relationships
- Avoiding logical fallacies in data analysis
By mastering these foundational concepts, you will be well-equipped to tackle a wide range of problems with greater confidence and clarity.
Practice Problems for Better Understanding
To reinforce your understanding of key concepts, working through practice problems is essential. These exercises help you apply what you’ve learned, identify gaps in your knowledge, and develop problem-solving strategies. By engaging with various scenarios, you’ll gain more confidence in your skills and improve your ability to tackle challenges effectively.
Sample Problems for Practice
Below are a few example problems designed to test your comprehension and application of critical concepts. Try solving them to enhance your understanding:
| Problem | Solution Approach |
|---|---|
| Calculate the mean of the following numbers: 2, 4, 6, 8, 10 | Sum all the numbers and divide by the total count (5). |
| Find the standard deviation of the data set: 5, 8, 12, 15, 20 | First, calculate the mean, then determine the variance and take the square root. |
| What is the probability of getting heads in a fair coin flip? | Probability is 1/2 since there are two equally likely outcomes (heads or tails). |
More Complex Problems
For more advanced practice, work on problems involving multiple variables or more complex distributions:
- Determine the correlation coefficient between two variables in a given data set.
- Use regression analysis to predict future outcomes based on current trends.
- Apply the binomial distribution to calculate the probability of a specific number of successes in a series of trials.
By consistently practicing these types of problems, you’ll develop a deeper understanding and refine your ability to tackle challenges in real-world scenarios.
Interpreting Graphs and Charts Correctly
Visual representations of data, such as graphs and charts, are powerful tools for understanding complex information. However, interpreting them accurately requires careful attention to detail. Misreading a chart or overlooking key elements can lead to incorrect conclusions. In this section, we’ll explore how to analyze graphs and charts effectively to ensure accurate interpretation.
Key Elements to Look For
When reviewing a graph or chart, consider the following aspects to understand the data properly:
- Labels and Titles: Always check the titles, axis labels, and legends to understand what the data represents.
- Scale and Range: Make sure the scale on the axes is consistent and correctly represents the data range.
- Outliers: Identify any data points that fall outside the expected range and consider their impact.
- Trends and Patterns: Look for upward or downward trends, clusters, or gaps that indicate significant relationships.
Common Types of Graphs and Their Interpretation
Different types of graphs serve different purposes. Here’s how to interpret the most common ones:
- Bar Graphs: Used to compare quantities across categories. Pay attention to the height of the bars and the axis labels.
- Line Graphs: Often used to show trends over time. Focus on the slope of the line and any sharp changes in direction.
- Pie Charts: Useful for showing proportions. Examine the size of the slices and their relationship to the whole.
- Histograms: Display the frequency distribution of data. Note the width of the bins and the distribution of data points.
By practicing the correct interpretation of graphs and charts, you will be able to draw accurate insights from visual data and make informed decisions based on it.
Tips for Managing Time During the Exam
Effective time management is crucial when you’re working under pressure. Learning how to allocate your time wisely can help you complete all tasks efficiently without feeling rushed. In this section, we’ll explore strategies for staying on track and ensuring that you have enough time for each part of the test.
Start by reviewing the instructions and the number of questions so you can estimate how much time to dedicate to each section. Prioritize the questions based on difficulty and length. If a question is too time-consuming, move on to the next one and return to it later if time permits. Using a watch or timer can help you stay aware of the passing time and prevent you from spending too much time on any single task.
Practice time management techniques during mock tests to build confidence and improve your pacing. With preparation and focus, you can approach the test methodically and finish all sections within the allotted time frame.
How to Approach Word Problems
Word problems can often seem intimidating, but breaking them down into manageable steps makes them much easier to solve. The key to tackling these problems lies in understanding the information presented, identifying what needs to be found, and applying the correct methods to arrive at a solution. By approaching word problems systematically, you can solve them more confidently and efficiently.
Steps for Solving Word Problems
Follow these steps to effectively approach and solve word problems:
- Read Carefully: Read the problem thoroughly to understand the scenario and identify important details.
- Identify Key Information: Underline or highlight the data points and variables that are relevant to the problem.
- Translate Words to Numbers: Convert the words and phrases into mathematical expressions or equations. Look for keywords such as “total,” “difference,” or “product” that indicate specific operations.
- Set Up an Equation: Based on the information, form an equation that represents the situation.
- Solve the Equation: Use appropriate mathematical methods to solve the equation and find the unknown value.
- Check Your Work: After finding the solution, double-check your calculations and ensure the answer makes sense in the context of the problem.
Example of a Word Problem
Here’s an example of a word problem and how to approach it:
| Problem | Solution Approach |
|---|---|
| If a car travels 60 miles per hour for 4 hours, how far will it travel? | Use the formula Distance = Speed × Time. Substitute the values: Distance = 60 × 4 = 240 miles. |
By following these steps and practicing regularly, you’ll become more comfortable and efficient at solving word problems, enabling you to tackle them with greater confidence during assessments.
Statistical Inference and Hypothesis Testing
Drawing conclusions from data involves more than just summarizing information. It requires making predictions or decisions about a larger population based on sample data. The process of statistical inference allows you to assess the strength of the evidence and determine whether observed results are due to chance or reflect a true underlying pattern. Hypothesis testing is one of the key methods used in this process to evaluate the validity of claims about a population.
Understanding Hypothesis Testing
Hypothesis testing involves two competing statements: the null hypothesis and the alternative hypothesis. The null hypothesis generally assumes no effect or no difference, while the alternative hypothesis suggests that an effect or difference exists. The goal is to gather enough evidence from the sample data to either reject the null hypothesis or fail to reject it.
To perform hypothesis testing, follow these steps:
- State the Hypotheses: Formulate the null hypothesis (H0) and the alternative hypothesis (Ha).
- Set the Significance Level: Choose a significance level (α), typically 0.05, which indicates the probability of rejecting the null hypothesis when it is true.
- Collect Data and Calculate Test Statistic: Use the appropriate statistical test (such as t-test, z-test, etc.) to analyze the sample data.
- Make a Decision: Compare the p-value to the significance level to determine whether to reject or fail to reject the null hypothesis.
- Conclusion: Based on the test result, conclude whether there is enough evidence to support the alternative hypothesis or if the null hypothesis stands.
Example of Hypothesis Testing
Consider an example where a company claims that their average product weight is 500 grams. To test this, you would:
- Null Hypothesis (H0): The mean weight is 500 grams.
- Alternative Hypothesis (Ha): The mean weight is not 500 grams.
- Collect a sample and perform a test (e.g., t-test) to calculate the p-value.
- If the p-value is less than the significance level (e.g., 0.05), reject the null hypothesis and conclude that the mean weight is different from 500 grams.
By understanding and applying hypothesis testing, you can make well-informed decisions about whether the evidence from a sample supports specific claims about a population.
Understanding Descriptive Statistics Techniques

Describing data effectively is essential for understanding patterns and drawing meaningful conclusions. By summarizing large datasets into manageable forms, you can highlight key features such as central tendencies, variation, and distribution. Descriptive methods help in visualizing, organizing, and interpreting data to get a clear understanding of its structure.
Key Measures of Central Tendency
Central tendency refers to the typical or central value in a dataset. The most commonly used measures are:
- Mean: The average of all values in a dataset. It is calculated by summing all values and dividing by the number of data points.
- Median: The middle value when the data is arranged in ascending order. It divides the dataset into two equal halves.
- Mode: The value that occurs most frequently in the dataset. A dataset may have one mode, multiple modes, or no mode at all.
Understanding Measures of Dispersion
Dispersion refers to the spread or variability of data. These measures help determine how much individual data points differ from the central value. Common techniques include:
- Range: The difference between the maximum and minimum values in the dataset.
- Variance: The average of the squared differences from the mean. It gives an indication of how spread out the data is.
- Standard Deviation: The square root of the variance, providing a measure of how much data points deviate from the mean on average.
These descriptive techniques form the foundation of data analysis, allowing you to summarize key aspects of the data and make informed interpretations. Whether you are comparing datasets, identifying trends, or simply understanding a distribution, mastering these methods is essential for accurate data analysis.
Key Terms Every Student Should Know
When working with data and analyzing various concepts, there are several key terms that are essential for understanding the foundational ideas behind the subject. Familiarity with these terms will not only help you grasp core concepts but also enable you to communicate your findings clearly and effectively. Below are some of the most important terms that every student should be well-versed in.
- Variable: A characteristic or attribute that can be measured or categorized. It can take different values depending on the data being analyzed.
- Population: The entire set of items or individuals that you are studying or drawing conclusions about.
- Sample: A subset of the population that is used to represent the whole. Samples are often analyzed to make inferences about the population.
- Parameter: A numerical characteristic that describes a population, such as the population mean or standard deviation.
- Statistic: A numerical characteristic that describes a sample, such as the sample mean or sample standard deviation.
- Correlation: A statistical relationship between two variables, indicating how one variable changes as the other does.
- Probability: A measure of the likelihood that a certain event will occur, ranging from 0 (impossible) to 1 (certain).
- Hypothesis: A testable statement or prediction about a relationship between variables, which can be tested using data.
- Distribution: The way in which the values of a variable are spread or arranged across a range of possible values.
- Outlier: An observation that lies an abnormal distance from other values in a dataset, which can skew results and interpretations.
Understanding these terms is crucial for anyone working with data. By mastering these concepts, you’ll be able to analyze and interpret information more effectively, as well as communicate your insights with clarity and precision.
Final Exam Question Types You May Face
When preparing for any test involving data analysis, it is important to be familiar with the different types of questions that you may encounter. These questions can vary in format and difficulty, but understanding the common types will help you approach the material with confidence. Below are some of the most common types of questions you may face during an assessment of this nature.
Multiple Choice Questions
Multiple choice questions typically present a statement or problem followed by several possible answers. You are required to choose the one that is correct. These questions often test your understanding of fundamental concepts and your ability to apply them to simple scenarios.
Short Answer Questions
Short answer questions usually require a brief, direct response, often asking you to define or explain specific terms or concepts. These types of questions assess your ability to recall key information and articulate it clearly and concisely.
Data Interpretation Questions

In these questions, you will be provided with graphs, tables, or charts, and you must interpret the data to answer the question. These questions assess your ability to extract relevant information from visual representations of data and draw conclusions based on that information.
Problem-Solving Questions
Problem-solving questions involve applying the concepts and formulas you have learned to solve real-world scenarios. These questions test your ability to think critically and methodically as you analyze a given problem and calculate the appropriate solution.
True or False Questions
True or false questions present a statement, and you must decide if the statement is accurate or inaccurate. These questions are designed to test your understanding of key principles and your ability to discern correct information from misconceptions.
Being prepared for these different types of questions will help you perform well on your test. Practicing these question formats and understanding the underlying concepts will make it easier to tackle any challenge that comes your way during the assessment.
Last-Minute Review Tips for Success
When the clock is ticking and you’re facing a time crunch before a major assessment, having a strategy in place is essential. Last-minute preparation doesn’t mean rushing through all the material, but rather focusing on the most critical concepts and honing your skills. Here are some tips that can help you make the most of the final hours leading up to your test.
Prioritize Key Concepts
In the final moments, it’s important to focus on the areas that are most likely to appear on the assessment. Identify the core topics you’ve covered and prioritize those that have the highest weight. Review notes, textbooks, and any practice problems related to these topics. Concentrating on high-yield material can make a big difference in your performance.
Practice Under Timed Conditions
Simulate the test environment by practicing problems under timed conditions. This will help you get used to working within the time constraints, improve your speed, and reduce anxiety on the day of the test. Set a timer and tackle as many practice questions as possible. Time management is a key factor in successfully completing the assessment.
Review Mistakes and Learn from Them
It’s easy to overlook mistakes when you’re rushing through practice problems, but identifying where you went wrong can be an invaluable part of your preparation. Review errors and understand why you made them. This helps you avoid repeating the same mistakes during the real test and reinforces your understanding of the material.
Stay Calm and Confident
Confidence can play a big role in your performance. Take a few moments to relax and clear your mind. Breathing exercises and positive affirmations can help you calm your nerves. Remember, last-minute preparation is not about cramming new information but reinforcing what you already know.
By focusing on these strategies, you can maximize your preparation in the last hours before your test. The key is to stay organized, stay calm, and focus on applying your knowledge effectively when the time comes.