
The first section of any mathematics course lays the groundwork for more complex topics that follow. It introduces essential skills and techniques that are crucial for solving problems efficiently. By understanding these basic principles, students can build a strong foundation for tackling more challenging material later on.
Throughout this section, you’ll encounter a variety of problems that require logical reasoning and systematic approaches. Whether you’re solving equations, working with functions, or applying mathematical rules, each exercise is designed to strengthen your problem-solving abilities. The key to success in these early lessons is to carefully follow each step and consistently practice the methods introduced.
It’s important to recognize the role these introductory concepts play in developing your mathematical fluency. With each correctly solved problem, you’ll gain confidence and a deeper understanding of the subject, preparing you for the more advanced topics ahead. Focus on mastering these skills, and you’ll be well-equipped to progress through the course with ease.
CPM Pre Calc Chapter 1 Solutions Overview
The first set of exercises introduces foundational concepts that are essential for progressing through the course. These problems are designed to familiarize students with essential skills such as solving equations, understanding functions, and applying mathematical principles to real-world situations. The goal is to establish a strong base, ensuring that learners are equipped with the necessary tools to tackle more complex problems in later sections.
Throughout this section, you will find various types of problems, each focusing on different aspects of mathematics. Some problems challenge your ability to manipulate algebraic expressions, while others require you to analyze and interpret data. Understanding the methods for solving these problems is crucial, as each type of exercise builds upon the previous one, increasing in difficulty as the section progresses.
Key Topics Covered
This section covers a wide range of fundamental topics, each aimed at strengthening specific mathematical skills:
| Topic | Description |
|---|---|
| Basic Algebraic Expressions | Introduction to variables, constants, and operations. |
| Linear Equations | Techniques for solving simple and multi-step equations. |
| Functions and Graphing | Understanding the relationship between variables and graphing functions. |
| Word Problems | Applying mathematical concepts to real-world situations. |
How Solutions Build Understanding
Each solution provides a detailed step-by-step explanation, demonstrating how to approach and solve various types of problems. By breaking down complex exercises into smaller, manageable steps, students gain clarity and build confidence. The examples included offer clear insights into applying mathematical principles to different scenarios, showing both the process and the rationale behind each solution.
Understanding Key Concepts in Chapter 1
The first section of this course serves as the foundation for the entire subject, introducing the essential principles and techniques that will be crucial as the material progresses. Mastery of these core concepts is vital, as they are frequently revisited in later topics. This section emphasizes clarity in problem-solving approaches, logical reasoning, and the ability to apply mathematical rules effectively in various scenarios.
Key ideas in this section revolve around building confidence with basic operations, simplifying complex expressions, and solving fundamental equations. By understanding the rules and methods behind these concepts, students can tackle more challenging problems in future lessons with greater ease and accuracy. Familiarity with these ideas also enhances analytical thinking and prepares students for real-world applications of mathematical concepts.
Important Principles to Focus On
Several essential principles form the backbone of this section, including:
- Algebraic Manipulations: Working with variables, constants, and expressions.
- Equation Solving: Techniques for solving linear and quadratic equations.
- Graphing Functions: Understanding how equations translate into visual representations on graphs.
- Word Problem Interpretation: Using algebraic methods to solve real-world problems.
How These Concepts Prepare You for Future Topics
The concepts introduced in this section are not only foundational but also serve as the stepping stones for more advanced ideas. The ability to simplify complex equations, graph mathematical functions, and interpret real-life scenarios with mathematical tools prepares students for the challenges in subsequent sections. Mastering these core concepts early on ensures a smoother transition into higher-level topics, allowing students to apply their knowledge with greater proficiency.
How to Approach Pre Calc Problems
When tackling mathematical problems, having a clear strategy is essential for success. By breaking down each problem into smaller, manageable steps, you can approach even the most complex tasks with confidence. The key is to identify the core components of the problem, apply appropriate methods, and double-check your work as you go. This structured approach helps prevent mistakes and ensures a more thorough understanding of the material.
As you begin solving problems, it’s important to stay organized. Whether working with equations, functions, or graphs, following a logical sequence of steps allows you to focus on each part of the problem systematically. This method not only helps in finding the correct solutions but also in understanding the reasoning behind them, which is crucial for mastering more advanced topics in the future.
Step-by-Step Process for Solving Problems
Here is a general approach that can help with most exercises:
- Identify Key Information: Start by carefully reading the problem and highlighting the important data.
- Choose the Right Method: Determine which mathematical concepts and formulas are most relevant to the task.
- Break Down the Problem: Divide the problem into smaller steps or subproblems to make it more manageable.
- Solve Step-by-Step: Follow a logical sequence, performing operations one at a time to reach the solution.
- Review the Solution: Check your work to ensure all steps were followed correctly and that the final answer makes sense.
Common Pitfalls to Avoid
While working through problems, there are several common mistakes to watch out for:
- Skipping Steps: Always follow the method completely to avoid missing critical details.
- Rushing Through the Problem: Take your time to fully understand each part of the problem before proceeding.
- Ignoring Units or Signs: Ensure that all units and negative signs are correctly handled throughout the process.
By adhering to these principles and staying focused on the task at hand, you’ll build a strong problem-solving mindset and develop the skills needed to tackle more complex exercises with ease.
Step-by-Step Guide to Solving Exercises
Solving mathematical exercises effectively requires a clear, organized approach. By following a systematic process, you can tackle even the most challenging problems with confidence. The goal is to break down each exercise into manageable steps, ensuring that every detail is addressed. This method not only leads to accurate solutions but also deepens your understanding of the underlying principles.
Each exercise presents a unique set of challenges, but the process for solving them remains largely consistent. Starting with understanding the problem, followed by applying the right techniques and verifying the results, ensures that you can solve any problem methodically. The more you practice this approach, the more intuitive it becomes, allowing you to solve problems faster and more accurately.
Follow these steps for an effective solution:
- Read and Understand the Problem: Carefully go through the exercise, identifying all the given information and what is being asked. This is the foundation for solving the problem.
- Choose the Appropriate Method: Based on the problem type, decide which mathematical technique or formula is best suited for the task.
- Solve Step-by-Step: Work through the problem one step at a time, ensuring each step is clear before moving forward.
- Double-Check Calculations: After completing the problem, review your steps to make sure there are no errors in your calculations or reasoning.
- Review the Final Solution: Make sure your final answer is both reasonable and correctly answers the original question.
By following this method, you can build confidence in your problem-solving abilities, leading to a better grasp of complex topics in the future. Each step reinforces the skills necessary to handle progressively more difficult exercises as you move forward in your studies.
Common Mistakes in Chapter 1
When working through introductory mathematical problems, it’s easy to overlook certain details or fall into common pitfalls. These mistakes can prevent students from fully understanding the material and hinder their progress. Being aware of these errors allows for better problem-solving and helps to avoid frustration when tackling exercises. The key is to develop a methodical approach and to always double-check your work before finalizing an answer.
As students begin to work with fundamental concepts, some of the most frequent mistakes occur in areas such as equation handling, interpreting problem statements, and overlooking key steps in the solution process. By identifying and correcting these errors early on, students can build a stronger mathematical foundation and gain confidence in their abilities.
Overlooking Key Steps
One of the most common mistakes is skipping steps during the solving process. It’s easy to jump from one part of the problem to the next without fully completing intermediate steps. This can lead to missed details and incorrect solutions. Taking the time to solve problems methodically, even when the steps seem straightforward, ensures no part of the process is overlooked.
Misinterpreting the Problem
Another frequent error is misreading or misunderstanding the question. Sometimes, key information is buried within the problem, and if not carefully considered, it can lead to incorrect assumptions. Always read the problem carefully and highlight important values or operations to ensure you’re addressing the correct question and using the right methods.
By avoiding these common mistakes and adhering to a structured approach, you’ll be better prepared to solve problems accurately and efficiently. Paying attention to detail and practicing regularly are essential for mastering the material and succeeding in future topics.
Tips for Mastering Pre Calc Foundations
Building a solid understanding of the basic principles in mathematics is essential for success in more advanced topics. These foundational skills not only provide a strong base for solving complex problems but also help develop critical thinking abilities. Mastering these core concepts requires consistent practice, careful attention to detail, and a methodical approach to each exercise.
To excel in this subject, it’s important to develop a deep understanding of the material, rather than just memorizing formulas or procedures. By applying these fundamental concepts in various contexts and problems, you’ll reinforce your learning and gain confidence in your skills. These tips are designed to help you build that mastery and avoid common pitfalls along the way.
Practice Regularly and Consistently

The key to mastering any subject is regular practice. Set aside time each day to work through exercises, review concepts, and challenge yourself with new problems. The more you practice, the more familiar the material will become, allowing you to solve problems more efficiently. Focus on quality, not just quantity–take time to understand each step of the solution process and learn from your mistakes.
Understand the “Why” Behind Each Step
Instead of simply memorizing formulas or algorithms, take the time to understand why each step is necessary. Understanding the rationale behind each method will make it easier to apply these techniques to a variety of problems. Try to connect new concepts with ones you’ve already learned, as this will help reinforce your understanding and make it easier to recall when needed.
By following these tips, you can develop a solid foundation that will not only help you succeed in this subject but also prepare you for more advanced topics in the future. Stay patient, keep practicing, and always strive to deepen your understanding of the material. The more you invest in mastering the basics, the more confident you will be as you move forward in your studies.
Breaking Down Complex Problem Types
When faced with a challenging problem, the key to success is breaking it down into simpler, more manageable components. Complex problems often appear intimidating at first, but by approaching them step by step, you can identify the underlying patterns and apply the right techniques. This structured approach not only makes the solution process more straightforward but also enhances your understanding of how different concepts interact.
Whether dealing with complicated equations, functions, or word problems, the process remains the same: deconstruct the problem, identify what is being asked, and use the appropriate methods to solve each part. Over time, this approach will improve your ability to tackle even more difficult problems with ease.
Step-by-Step Breakdown of a Complex Problem
Here’s a simple guide to breaking down difficult problems:
| Step | Description |
|---|---|
| 1. Identify Key Information | Read the problem carefully and extract the important details, such as variables, constants, and operations. |
| 2. Simplify the Problem | Look for ways to simplify the expressions or equations. This might involve factoring, combining like terms, or reducing fractions. |
| 3. Apply Relevant Methods | Choose the correct method based on the problem type, such as substitution, elimination, or graphing techniques. |
| 4. Solve Step-by-Step | Work through the problem incrementally, checking each step as you go to ensure accuracy. |
| 5. Verify and Review | After arriving at the solution, review the steps to ensure no mistakes were made and that the answer is logical. |
Common Problem Types and Solutions
There are various types of problems that often appear in exercises. Here are some examples of common challenges and strategies for solving them:
| Problem Type | Solution Strategy |
|---|---|
| Solving Linear Equations | Isolate the variable by using inverse operations. Always check for possible solutions that make the equation true. |
| Quadratic Equations | Use factoring, completing the square, or the quadratic formula to find the roots. |
| Graphing Functions | Plot points based on the function and identify key features like intercepts, slopes, and asymptotes. |
| Word Problems | Translate the problem into an algebraic expression, then solve it using appropriate mathematical techniques. |
By breaking down complex problems into smaller parts and applying the correct methods, you can tackle even the most difficult exercises with confidence. This approach will not only help you find the right solution but also deepen your understanding of mathematical principles and their applications.
How to Check Your Answers Effectively
After completing a mathematical problem, it’s crucial to verify your solution to ensure its accuracy. This step helps to identify any potential errors made during the process and confirms that the final result answers the original question correctly. A systematic approach to checking your work can significantly reduce mistakes and increase your confidence in the solution.
There are various techniques you can use to effectively check your solutions. These methods help ensure that each step of the problem-solving process was done correctly and that the final result is valid. Below are some practical strategies to check your answers with confidence.
1. Review Each Step
- Go through each step of your solution carefully to ensure you didn’t skip any important details.
- Make sure all operations were performed correctly and that no steps were missed or rushed.
- Check if you applied the right method and formulas at each stage of the process.
2. Use a Different Approach
- If possible, solve the problem using an alternative method or formula to see if you reach the same answer.
- For example, if you used substitution in an equation, try using elimination or graphing to verify your solution.
- This helps to confirm that the result is consistent across different approaches.
3. Plug the Solution Back Into the Original Problem
- Substitute your solution back into the original equation or problem statement.
- If your solution satisfies the equation or answers the question correctly, it’s likely correct.
- This is one of the most reliable methods for verifying your answers, especially in algebraic problems.
4. Estimate Before Finalizing
- Before performing any detailed calculations, make a rough estimate of the answer to ensure it’s reasonable.
- This can be done by approximating values or checking the magnitude of the expected result.
- If your final answer significantly differs from the estimate, it’s worth reviewing the steps.
5. Check for Common Errors

- Look out for common mistakes such as sign errors, miscalculations, or wrong interpretations of the problem.
- Ensure that all units, exponents, and coefficients are consistent throughout the solution.
- Make sure you didn’t make any simple arithmetic or algebraic errors during calculations.
By following these strategies, you can effectively check your answers and identify any errors before submitting or finalizing your work. The more you practice these techniques, the more intuitive they will become, ultimately leading to better accuracy and understanding in your problem-solving process.
Using Graphing Techniques in Chapter 1
Graphing is an essential tool for visualizing mathematical concepts and relationships, especially when working with functions and equations. It allows you to gain a deeper understanding of the problem by providing a visual representation that can reveal patterns, intercepts, and other key features. This technique is invaluable for solving problems that involve identifying the behavior of functions or determining solutions graphically.
In many problems, graphing serves as an effective method for confirming algebraic solutions, testing hypotheses, and observing the interplay between variables. By plotting points, analyzing slopes, and identifying key intercepts, graphing techniques enable you to verify your results and build a stronger foundation in mathematical problem-solving.
Identifying Key Features of Graphs
When graphing a function or equation, it is important to identify the following key features:
- Intercepts: Points where the graph crosses the x-axis or y-axis.
- Slopes: The rate at which the function changes, especially for linear equations.
- Asymptotes: Lines the graph approaches but never touches, particularly in rational functions.
- Turning Points: Points where the function changes direction, important in higher-degree polynomials.
Graphing Linear and Non-Linear Functions
Graphing both linear and non-linear functions requires different techniques. For linear functions, plotting two points is often sufficient to draw the entire graph. For non-linear functions, such as quadratics or exponentials, you may need more points or a calculator to assist in plotting the graph accurately. Understanding the general shape of the graph (whether it’s a straight line, curve, or other shape) can guide you in plotting the points and visualizing the function’s behavior.
By applying graphing techniques, you can gain a clearer understanding of the solutions and the relationships between the variables in a problem. Whether you are solving equations or analyzing data, graphing serves as a valuable tool in the problem-solving process, enhancing your overall mathematical proficiency.
Understanding Functions and Equations
In mathematics, functions and equations are fundamental concepts that help us model and solve real-world problems. Functions describe relationships between two variables, where each input corresponds to exactly one output. Equations, on the other hand, represent statements of equality, often involving one or more variables, and they are used to express relationships or solve for unknown values. Understanding these concepts is essential for progressing in more complex mathematical topics and for solving a wide range of problems efficiently.
Grasping the core principles of functions and equations involves recognizing how variables interact and how their relationships can be expressed mathematically. This knowledge forms the foundation for algebra, calculus, and many other fields of mathematics.
Key Features of Functions
A function is defined by several key characteristics:
- Domain: The set of all possible input values for the function.
- Range: The set of all possible output values that the function can produce.
- Mapping: The process by which each input is associated with exactly one output.
- Graph: A visual representation of a function, showing the relationship between inputs and outputs on a coordinate plane.
Solving Equations
Equations are used to express relationships between variables and solve for unknowns. To solve an equation, you need to isolate the variable on one side of the equation. This often involves a series of operations, such as:
- Adding or subtracting: Simplifying terms to combine like terms or eliminate constants.
- Multiplying or dividing: Using inverse operations to isolate the variable or simplify the equation.
- Factoring: Breaking down polynomials into simpler components to solve for unknown values.
Understanding the structure of equations and how to manipulate them is crucial for solving problems in algebra, physics, economics, and many other fields. The ability to recognize patterns in equations and apply appropriate methods will significantly enhance your problem-solving skills.
Working Through Word Problems with Confidence
Word problems can initially seem overwhelming, but they are simply a way of translating real-world situations into mathematical equations. The key to solving these problems with confidence is to approach them systematically and break them down into manageable steps. By focusing on understanding the problem’s context and identifying the variables, you can simplify even the most complex scenarios.
Developing a methodical approach to word problems helps to clarify the steps needed to find a solution. With practice, this process becomes intuitive and allows you to tackle problems with greater ease. The following strategies can help you work through word problems effectively and build confidence in your problem-solving abilities.
Step-by-Step Strategy for Word Problems
When approaching a word problem, follow these steps:
- Read the Problem Carefully: Understand what is being asked and highlight important details or numbers.
- Identify the Variables: Determine which quantities in the problem are known and which ones need to be found.
- Write an Equation: Translate the verbal information into a mathematical equation or expression.
- Solve the Equation: Use appropriate algebraic methods to solve for the unknown variable.
- Check the Solution: Review the solution by substituting it back into the original problem to ensure it makes sense in context.
Common Pitfalls to Avoid
While solving word problems, there are a few common mistakes to watch out for:
- Misinterpreting the Question: Ensure you fully understand what the problem is asking before attempting to solve it.
- Forgetting Units: Pay attention to units of measurement and convert them if necessary to keep the equation consistent.
- Overcomplicating the Problem: Break down the problem into simpler parts to avoid unnecessary confusion.
- Not Checking the Answer: After solving, always verify your answer to make sure it is reasonable and correct.
By following a structured approach and avoiding common mistakes, you can solve word problems confidently and accurately. With practice, your ability to translate real-world situations into solvable equations will improve, making mathematical problem-solving a more intuitive and rewarding experience.
Helpful Resources for Pre Calc Chapter 1
When working through foundational mathematical topics, having access to the right resources can make all the difference. There are various tools, both online and offline, that can help deepen your understanding and clarify complex concepts. Whether you prefer interactive guides, video tutorials, or practice exercises, utilizing these resources effectively can significantly improve your skills and confidence in solving problems.
It’s important to identify the resources that align with your learning style. Some students may benefit from visual explanations, while others might prefer written explanations or interactive practice sessions. Below, we explore a variety of helpful resources that cater to different needs and learning preferences.
Online Tools and Tutorials
The internet is full of platforms offering valuable support for learners at all levels. Some of the most useful tools include:
- Khan Academy: A popular platform that provides free video lessons on a wide range of topics, including foundational mathematics. Its step-by-step explanations and exercises can help reinforce key concepts.
- Wolfram Alpha: An advanced computational engine that can solve mathematical problems and provide detailed step-by-step solutions. It’s an excellent resource for checking work and understanding how to approach different types of problems.
- PatrickJMT: A website with video tutorials covering various math topics, including the basics and more advanced techniques. The concise explanations help clarify difficult concepts.
Books and Practice Guides

If you prefer more traditional methods of study, several textbooks and practice guides are designed to help reinforce mathematical skills. These resources often provide numerous practice problems with solutions, allowing you to hone your problem-solving abilities. Some recommended books include:
- Algebra 1 by McDougal Littell: A well-structured textbook with clear explanations and exercises to build a solid foundation in algebra and related topics.
- Schaum’s Outlines: This series of books offers a wide range of math topics with thousands of practice problems and detailed solutions, ideal for mastering various mathematical concepts.
By incorporating these resources into your study routine, you can gain a deeper understanding of the material and enhance your problem-solving skills. Whether through online tools or textbooks, these materials are designed to provide the guidance and practice needed to excel in your mathematical studies.
Learning from Examples in the Textbook
Textbooks provide an essential resource for mastering new concepts, and one of the most valuable sections is the set of worked examples. These examples illustrate step-by-step how to approach a particular type of problem, offering a clear roadmap for solving similar challenges. By carefully reviewing these examples, students can learn effective strategies, understand key principles, and avoid common mistakes in problem-solving.
It is important to not just passively read through the examples, but to engage with them. Try to replicate the steps on your own, identifying each action and its purpose. This active engagement helps reinforce your understanding and ensures that the methods demonstrated are internalized. As you work through different examples, you’ll become more confident in your ability to apply these techniques to new problems.
Moreover, most textbooks provide practice problems that closely follow the examples, allowing students to test their understanding and apply what they’ve learned. These exercises offer a great way to practice the steps and techniques introduced in the examples, and by solving them, you reinforce the learning process. Make it a habit to revisit the examples after attempting the exercises, comparing your methods and results with the textbook solutions.
How to Prepare for the Test
Preparing effectively for an upcoming assessment is crucial for success. To ensure you perform well, it’s important to take a systematic approach to reviewing the material, practicing problem-solving, and sharpening your understanding of key concepts. This section outlines the steps you can follow to enhance your readiness and boost your confidence before the test.
The first step in your preparation is to review the topics that will be covered. Identify the key areas from your lessons, homework, and practice exercises. Take time to understand the most important concepts and formulas that are likely to appear in the test. Make sure you are clear on both theoretical concepts and practical applications.
Once you know what to focus on, create a study schedule that breaks down your review sessions into manageable blocks of time. This will help you stay on track and ensure that you cover all necessary material. It is essential to balance your time between reading notes, practicing problems, and testing yourself under real exam conditions.
| Study Phase | Action Plan |
|---|---|
| Concept Review | Go over the essential topics that will be tested. Focus on understanding the underlying principles, and take notes on key formulas and methods. |
| Practice Problems | Work through various examples and exercises. Aim to complete a range of question types to become familiar with different problem-solving techniques. |
| Timed Simulations | Set aside time to take mock exams or practice under timed conditions. This will help improve your time management skills and familiarize you with the exam format. |
| Clarify Questions | If there are areas you are uncertain about, ask your teacher, tutor, or classmates for help. Understanding difficult concepts will build your confidence. |
| Analyze Mistakes | Review any errors made in practice problems or mock tests. Understand why you got them wrong and learn how to avoid similar mistakes in the future. |
By following a structured approach and focusing on consistent practice, you will strengthen your understanding and improve your performance on the test. Stay positive and dedicated to your preparation, and you’ll be well-equipped for success when the test day arrives.
Practice Strategies for Success
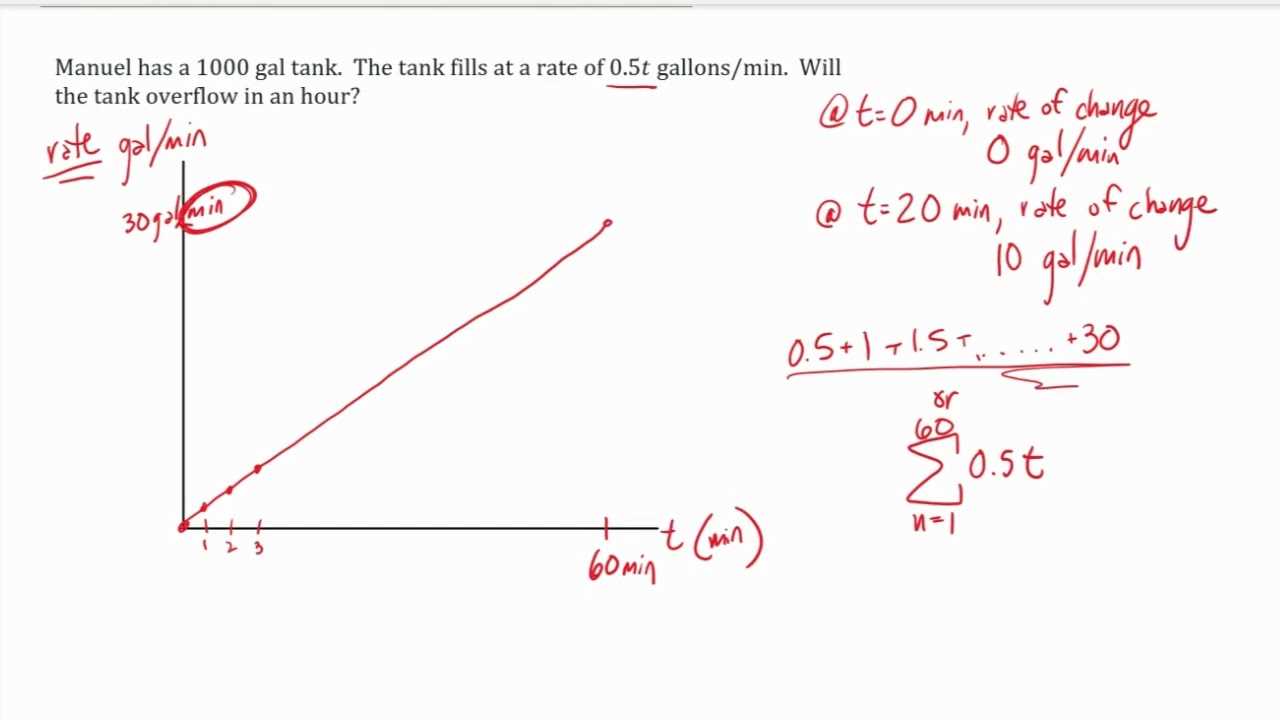
Effective practice is key to mastering any subject. To succeed, it’s essential to approach exercises strategically, ensuring you strengthen both your understanding and problem-solving abilities. This section outlines various practice techniques that will help you maximize your learning and build the confidence needed to excel in assessments.
Start by organizing your study materials. Break down the content into smaller, digestible sections and focus on one topic at a time. This method allows you to dive deeper into specific concepts and gain a clear understanding of each before moving on to the next. As you practice, aim for a mix of different problem types to ensure you’re ready for anything that might appear in an assessment.
One effective practice method is active recall. Instead of simply reviewing notes or looking at solved examples, try solving problems on your own without referring to the solution immediately. This helps to reinforce your memory and improves your ability to retrieve information quickly during a test.
Another useful strategy is spaced repetition. Spread your practice sessions over several days or weeks, revisiting previously learned material regularly. This technique helps combat forgetting and solidifies your long-term understanding of key concepts.
Additionally, focus on understanding the underlying principles, not just memorizing formulas. Being able to explain why certain methods work will help you apply your knowledge more flexibly in a variety of contexts. Use visual aids like graphs and charts to support your understanding and enhance memory retention.
Finally, after completing practice problems, always take the time to review your mistakes. Analyzing where you went wrong will help you avoid repeating the same errors and will provide valuable insights into areas that require further attention.
By implementing these practice strategies, you will strengthen your skills and approach assessments with greater confidence. Consistency and reflection are key to ensuring your success over time.
Real-World Applications of Mathematical Concepts
Mathematical concepts are not just theoretical; they play a significant role in a variety of real-world scenarios. Understanding how to apply mathematical principles helps bridge the gap between abstract knowledge and practical use. From finance to engineering, these concepts are crucial tools for solving complex problems in everyday life and in various professional fields.
Applications in Engineering and Technology
One of the most impactful areas where mathematical concepts are applied is in engineering. Whether designing bridges, cars, or software systems, engineers use advanced mathematical methods to solve problems related to structure, design, and optimization. Some of the specific applications include:
- Modeling physical systems: Mathematical models help engineers simulate real-world conditions and predict how structures will behave under stress.
- Optimizing designs: By applying principles of geometry and algebra, engineers can minimize material waste while maximizing the strength and efficiency of their designs.
- Signal processing: In electrical engineering, mathematical functions are used to filter and interpret signals, ensuring that communications systems work effectively.
Applications in Finance and Economics
In the world of finance, mathematical concepts are used to analyze investments, forecast market trends, and manage risks. The understanding of functions and equations helps professionals model financial systems, calculate interest rates, and make data-driven decisions. Key areas of application include:
- Investment analysis: Mathematical functions help in determining the value of an investment over time, accounting for factors such as compound interest and inflation.
- Risk management: Probability and statistics are applied to predict the likelihood of various financial outcomes and to manage portfolio risk.
- Market forecasting: Economists use regression analysis and other mathematical methods to predict trends in markets, guiding investment strategies and policy decisions.
By understanding and applying these mathematical tools, professionals in diverse fields can make informed decisions and optimize their work processes, ultimately contributing to innovation and success in their industries.
How to Track Progress in Mathematical Studies
Monitoring your development in mathematical studies is essential for ensuring that concepts are understood and retained. By actively tracking your progress, you can identify strengths, address areas of difficulty, and stay motivated throughout your learning journey. There are several strategies to effectively track your improvement and make continuous advancements.
Key Methods for Tracking Progress
Here are some practical ways to assess and track your progress in mathematics:
- Reviewing Completed Exercises: Regularly revisit exercises you’ve completed to check for mistakes and areas where understanding can be enhanced. This will help you spot patterns and recognize where you may need additional practice.
- Taking Practice Tests: Simulating test conditions with practice exams allows you to gauge your understanding of the material under time constraints, providing a more accurate reflection of your abilities.
- Setting Specific Goals: Break down larger topics into smaller, manageable goals. Set targets such as mastering a particular function or completing a set number of problems each week to stay on track.
Tracking Tools and Resources
Using tools and resources to track your learning can be incredibly beneficial. Here are some options to consider:
- Progress Charts: Create a chart or spreadsheet to log your completed exercises, quiz scores, and practice test results. This will give you a visual representation of your improvements over time.
- Math Journals: Keeping a journal to write down your thoughts, strategies, and reflections on each topic can help reinforce learning and highlight areas that need more attention.
- Online Learning Platforms: Many digital platforms offer interactive exercises and progress tracking features. These tools can provide instant feedback, allowing you to identify where you’re excelling and where you may need more practice.
By combining these strategies and tools, you can effectively monitor your growth and ensure you stay on track to achieving your goals in mathematics.