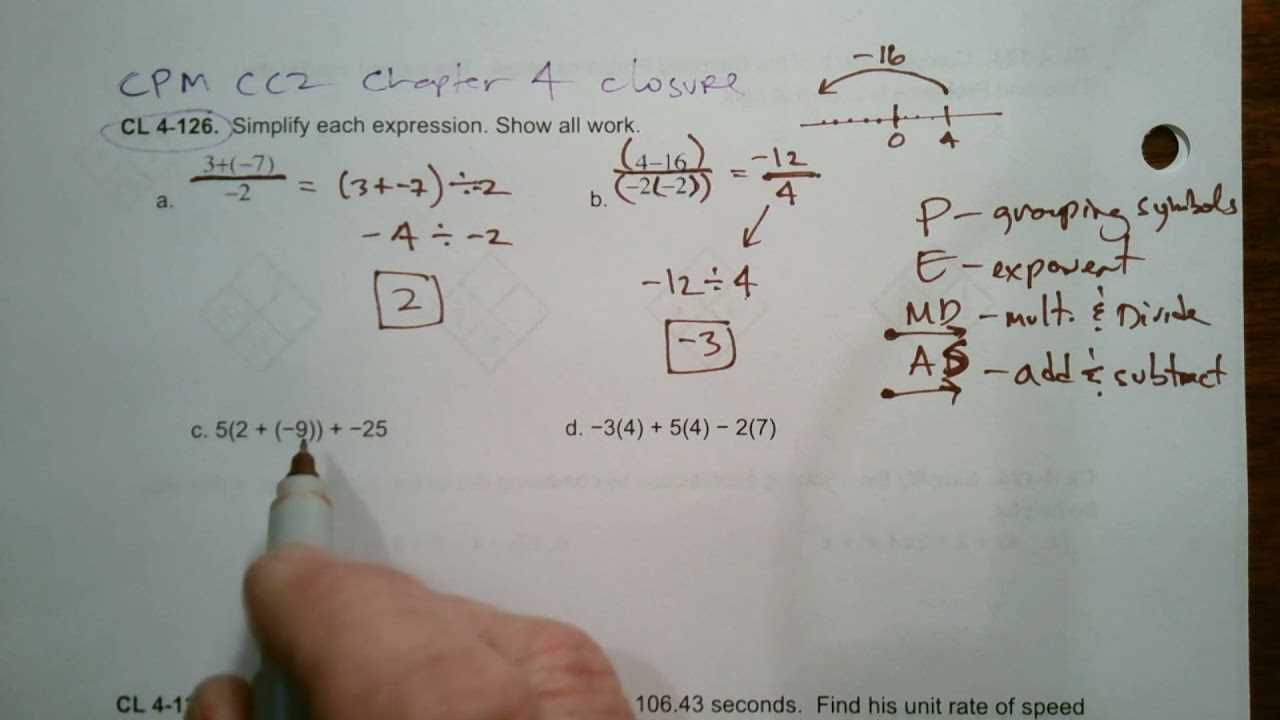
In this section, we delve into essential problem-solving techniques that will guide you through various complex tasks. It focuses on building a solid foundation by breaking down challenges into manageable steps. This approach helps ensure clarity and precision as you work through each exercise.
Mastering the material requires more than just memorization; it involves understanding underlying principles and applying them to solve problems effectively. Whether you are revisiting concepts or tackling new ones, the goal is to enhance your ability to approach problems with confidence and accuracy.
Grasping the core principles is crucial, as it sets the stage for more advanced topics. By focusing on practical examples and real-world applications, you will be able to see how these strategies function beyond theoretical knowledge. Effective problem-solving skills are the key to progressing and succeeding in your studies.
Cpm Chapter 2 Answers
This section focuses on providing clarity and practical insights for solving various mathematical problems and exercises. The emphasis is on guiding you through the process of understanding and applying key concepts effectively. Each problem is broken down into manageable steps to enhance comprehension and accuracy.
By carefully analyzing each example, you will learn the thought process behind finding solutions. This approach not only improves your problem-solving skills but also strengthens your ability to tackle more complex scenarios in future tasks. It’s about building a systematic understanding that can be applied to a wide range of challenges.
The goal is to ensure that every step is clear and comprehensible, offering you the tools to solve similar problems independently. With the right techniques and strategies, you will be equipped to handle any difficulty that arises, allowing you to approach tasks with confidence and precision.
Understanding Key Concepts in Chapter 2
This section aims to explore fundamental ideas that form the basis of the problems presented. By breaking down the core principles, it provides a clear pathway for understanding and applying the concepts. The focus is on making sure that each idea is thoroughly grasped, setting the stage for tackling more complex challenges later on.
Grasping these essential concepts is crucial for building a strong foundation. Whether it’s identifying patterns or recognizing the relationship between variables, understanding the core mechanics is the first step toward successfully solving problems. The goal is to shift from rote memorization to a deeper understanding that can be applied in various contexts.
Once the key principles are understood, it becomes easier to work through exercises with confidence. By focusing on how these concepts interact and support each other, you’ll be better equipped to approach similar tasks in the future with a systematic method.
Step-by-Step Solutions for Chapter 2
This section provides a detailed breakdown of the solutions for each problem, ensuring that you can follow the process from start to finish. By dissecting each step, it becomes easier to understand how to approach similar exercises on your own. The methodical approach helps clarify any confusion and reinforces learning.
Step 1: Analyzing the Problem
The first step in solving any problem is to carefully read and analyze the given information. Identify the key elements and figure out what is being asked. This step ensures that no crucial details are overlooked, laying a solid foundation for the solution process.
Step 2: Applying the Right Techniques
Once the problem is understood, apply the appropriate techniques to find a solution. This could involve using formulas, drawing diagrams, or breaking the problem into smaller parts. The goal is to use systematic methods to simplify complex situations.
| Step | Action | Purpose |
|---|---|---|
| 1 | Analyze the problem | Understand the key information and what is being asked. |
| 2 | Apply techniques | Use appropriate methods to simplify and solve the problem. |
| 3 | Verify the solution | Check the results to ensure accuracy and consistency. |
Following these steps ensures a structured approach, reducing errors and making the problem-solving process more efficient. As you practice, you will develop a deeper understanding of how to tackle various challenges with confidence.
How to Approach Chapter 2 Problems
To effectively solve problems in this section, it’s crucial to adopt a structured approach. By breaking down each problem into smaller, more manageable steps, you can avoid feeling overwhelmed and increase the likelihood of finding the correct solution. This approach allows you to focus on understanding the process rather than just memorizing methods.
Step 1: Understand the Problem
The first step is always to fully grasp the problem. Take time to read through the given information and identify the key elements. Understanding what is being asked and what is provided sets the stage for solving the problem efficiently.
- Read the problem carefully and underline important details.
- Identify what is unknown and what needs to be determined.
- Look for any constraints or limitations in the problem.
Step 2: Choose the Right Strategy
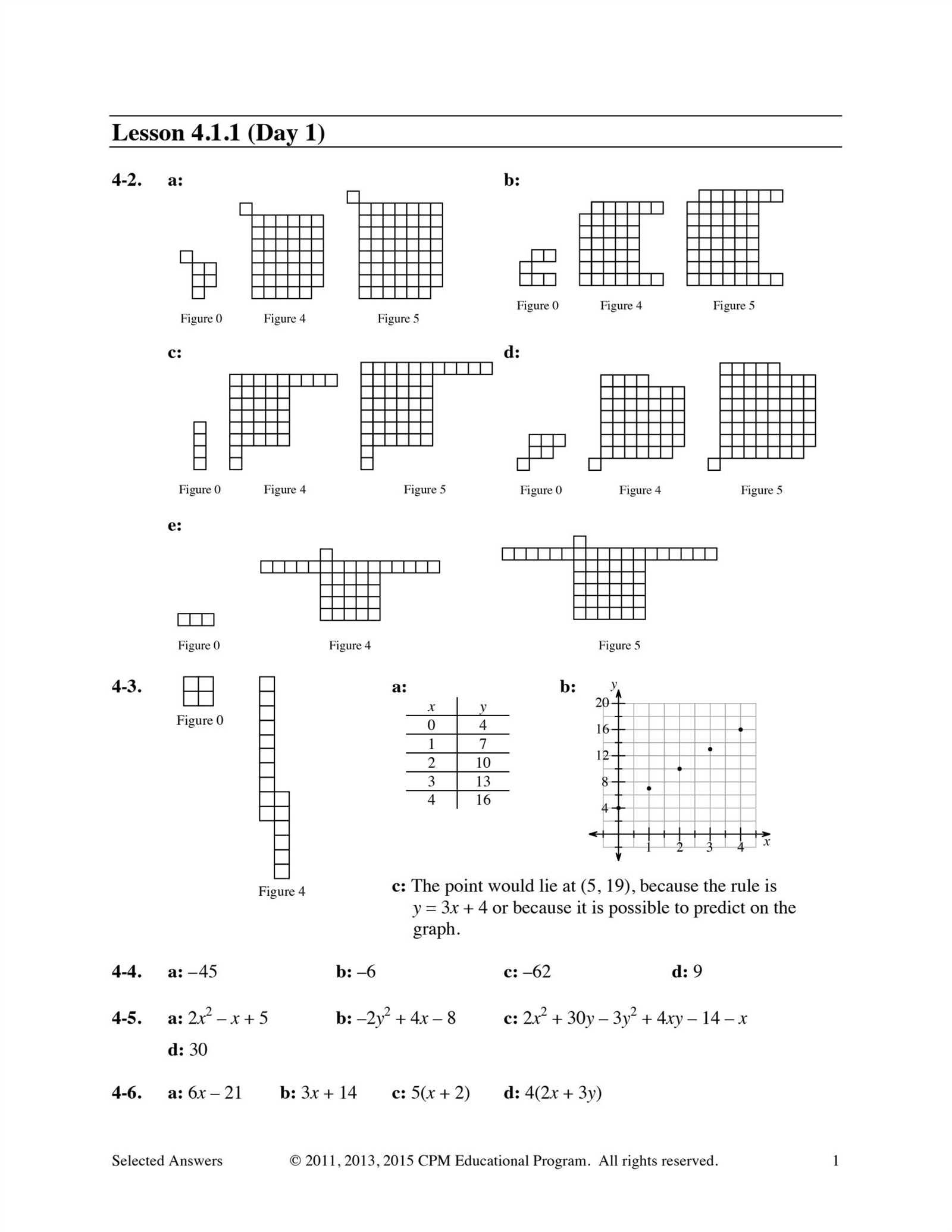
Once you understand the problem, the next step is selecting the appropriate method to solve it. This could involve using formulas, drawing diagrams, or breaking the problem into smaller pieces. By having a clear strategy, you can make the process more efficient and reduce the risk of errors.
- Determine which formulas or principles apply to the problem.
- Consider drawing a diagram or chart to visualize the problem.
- Break down the problem into smaller, simpler parts to solve it step by step.
By following this systematic process, you will be better prepared to approach similar problems with confidence and accuracy, improving both your understanding and your problem-solving skills.
Common Mistakes in Cpm Chapter 2
When working through the problems in this section, it’s easy to make errors that can lead to incorrect solutions. These mistakes often arise from overlooking key details, applying the wrong techniques, or rushing through steps without fully understanding the problem. Recognizing and avoiding these common pitfalls is essential for improving accuracy and mastering the material.
- Misinterpreting the problem: Often, the most common mistake is misunderstanding what the problem is asking. Carefully reading and identifying key terms is crucial.
- Skipping steps: In the rush to finish, it’s tempting to skip intermediate steps. This can lead to miscalculations and incomplete solutions.
- Incorrect use of formulas: Applying formulas incorrectly is a frequent issue. Always ensure you’re using the right formula for the given situation.
- Failure to check work: Not double-checking your answers can result in overlooked mistakes, especially in complex problems.
By staying aware of these mistakes, you can approach problems with more focus and precision. Here are some additional strategies to avoid common errors:
- Always read the problem carefully and highlight key information.
- Work through each step methodically to avoid skipping crucial parts.
- Verify the use of formulas and methods before proceeding.
- Review your answers to ensure consistency and correctness.
Being mindful of these potential mistakes will help you approach each problem more confidently and reduce the likelihood of errors as you progress through the exercises.
Tips for Mastering Chapter 2 Answers
Mastering the problems in this section requires more than just completing the exercises. It’s about developing a deep understanding of the material and honing your problem-solving skills. By applying a few key strategies, you can improve your ability to tackle complex tasks and work through challenges with confidence.
Practice Consistently
One of the most effective ways to improve is consistent practice. The more problems you solve, the better you will become at recognizing patterns and applying the right techniques. Focus on understanding the process rather than simply memorizing steps.
- Work on problems regularly to reinforce your learning.
- Start with easier exercises and gradually increase the difficulty.
- Review solutions to understand different approaches to problems.
Focus on Conceptual Understanding
Understanding the underlying principles is essential for success. Don’t just memorize formulas–take the time to understand why they work and how they apply to different scenarios. This will help you approach new problems with a clearer perspective and improve your ability to solve them.
- Ask questions to deepen your understanding of key concepts.
- Use visual aids like diagrams to enhance your comprehension.
- Link new knowledge to what you’ve already learned for better retention.
By practicing regularly and focusing on the concepts behind the tasks, you will be well on your way to mastering the material and improving your overall problem-solving skills.
Key Strategies for Solving Problems
Approaching problems strategically is essential for finding accurate solutions efficiently. The key to solving any complex task lies in breaking it down into smaller, more manageable steps, allowing you to focus on each part individually. By using proven strategies, you can ensure that you apply the right methods and techniques to arrive at the correct answer every time.
- Understand the Problem: Take the time to read and analyze the question carefully. Identify what information is given and what needs to be found. Understanding the task thoroughly is the first step toward solving it.
- Plan Your Approach: Before jumping into calculations or solutions, think about the best way to solve the problem. Choose the most appropriate method and prepare a step-by-step plan.
- Break it Down: Complex problems can often seem overwhelming. Divide them into smaller, simpler tasks to make the process easier and to ensure you don’t miss important details.
- Check Your Work: Once you’ve found a solution, take the time to review it. Double-check your steps, ensure consistency, and confirm that the result matches the conditions of the problem.
By following these strategies, you will develop a more systematic approach to solving problems, allowing you to tackle new challenges with confidence and precision.
Breakdown of Important Formulas
In this section, we will explore some of the most important formulas used to solve problems effectively. Understanding these formulas and how to apply them is essential for tackling complex tasks and finding accurate solutions. By breaking down each formula into its components, you can better understand how they work and how to use them in different scenarios.
Formula 1: The General Equation
This formula is one of the most fundamental tools used in problem-solving. It provides a framework for relating different variables and allows you to calculate unknown values. By understanding the relationship between the components, you can apply this equation to a wide variety of problems.
- Example: If the problem involves calculating speed, the general equation is: Speed = Distance / Time.
- Key Concept: By rearranging the equation, you can solve for any of the three variables: Distance, Time, or Speed.
Formula 2: The Area Formula
For problems involving geometry, the area formula is often essential. This formula is used to calculate the area of various shapes and is applicable in many different scenarios.
- Example: The area of a rectangle is calculated using: Area = Length x Width.
- Key Concept: Ensure you are using the correct measurements (inches, centimeters, etc.) to avoid errors in calculation.
By familiarizing yourself with these and other essential formulas, you can solve problems more efficiently and with greater confidence, knowing exactly how to apply the right formula in any given situation.
Practical Examples in Cpm Chapter 2
Applying theoretical knowledge to real-world problems is essential for mastering any subject. In this section, we’ll explore several practical examples that demonstrate how to use the concepts learned in the earlier sections to solve common problems. These examples will provide insight into how to approach tasks step-by-step, helping you to better understand how the theories work in practice.
Through these examples, you will learn how to identify key components of each problem, choose the correct methods, and apply relevant formulas to find the solution. These scenarios are designed to make the concepts more tangible and show how they can be used in various situations.
Example 1: Solving for Distance
In a scenario where you are asked to determine the distance traveled by a moving object, you can use the basic formula for speed:
- Given: A car moves at a speed of 60 miles per hour for 2 hours.
- Formula: Distance = Speed x Time
- Calculation: Distance = 60 miles/hour x 2 hours = 120 miles
This example shows how to apply a basic formula to determine the total distance traveled based on speed and time.
Example 2: Calculating the Area of a Triangle

Another common problem involves calculating the area of geometric shapes. For a triangle, the area formula is:
- Given: A triangle with a base of 10 units and a height of 5 units.
- Formula: Area = 1/2 x Base x Height
- Calculation: Area = 1/2 x 10 x 5 = 25 square units
This example demonstrates how to calculate the area of a simple geometric shape by applying the correct formula, making it easier to handle similar problems in the future.
By working through practical examples like these, you can build a deeper understanding of how to apply mathematical concepts in real-life situations, reinforcing your problem-solving skills.
How to Check Your Work Effectively
Ensuring that your solutions are correct is an essential step in problem-solving. Simply finishing a task doesn’t guarantee that it’s error-free. A thorough review process allows you to identify mistakes, verify your calculations, and confirm that all steps were followed correctly. By developing an effective checking method, you can greatly improve the accuracy of your work.
- Review the Problem: Before checking your solution, revisit the original problem. Make sure you understand what was asked and ensure that you have addressed every part of the task.
- Recheck Your Calculations: Go over your calculations step-by-step. Look for any mathematical errors such as incorrect arithmetic or missed signs. It’s easy to overlook simple mistakes, so double-checking is crucial.
- Verify Units and Labels: Ensure that all units are consistent and properly labeled throughout your work. Pay attention to conversions, especially when dealing with different measurement systems.
Use a Different Method for Verification
If possible, try solving the problem using a different method or approach. This can help you catch any errors that might have been made in the initial solution. If the answers match, you can be more confident in your result.
- Alternative Approach: For example, if you used a formula, try a graphical method or estimate the result to see if it aligns.
- Cross-Verification: Check your results with a trusted source or solution manual if available.
By consistently applying these strategies to check your work, you’ll not only reduce errors but also develop a more methodical approach to problem-solving that increases confidence in your results.
Best Practices for Chapter 2 Exercises
Approaching exercises effectively requires not just the right techniques but also a structured strategy to ensure you understand the material deeply and avoid common mistakes. By following a set of proven practices, you can maximize your learning and improve your ability to solve complex problems. These best practices will guide you through the process of tackling exercises with confidence and precision.
- Read Instructions Carefully: Before diving into any exercise, take the time to thoroughly read and understand the problem statement. This helps avoid missing important details that could affect your solution.
- Break Down the Problem: Don’t try to solve the entire problem in one go. Break it into smaller, manageable steps. This approach makes the problem easier to handle and ensures you address each part correctly.
- Work Step-by-Step: Always follow a logical sequence of steps. Avoid skipping stages in your calculations, as this can lead to errors. Writing out each step helps you track your thought process and catch mistakes.
- Use Visual Aids When Necessary: Diagrams, graphs, and tables can provide valuable insight into a problem. Visual representations often help clarify complex relationships between variables and simplify the solution process.
Review and Refine
After completing an exercise, take time to review your solution. Check if your answer makes sense in the context of the problem. Consider if there’s a simpler or more efficient way to approach it. Refining your methods over time will improve your overall skill level.
- Double-Check Calculations: Verify each calculation step for accuracy. Look for small mistakes such as sign errors or skipped operations.
- Practice Consistently: Regular practice is key to mastering exercises. The more problems you solve, the more proficient you’ll become at recognizing patterns and applying concepts.
By incorporating these best practices, you’ll not only enhance your ability to solve problems but also build a stronger understanding of the concepts behind the exercises, leading to better long-term success.
Clarifying Difficult Concepts in Chapter 2
Some topics can be particularly challenging, and understanding them requires breaking them down into simpler components. When facing complex ideas, it is important to identify the underlying principles and tackle them step-by-step. By doing so, you can clear up confusion and gain a deeper understanding of the material. Here, we will focus on strategies for making tough concepts more approachable and less intimidating.
Identify Key Areas of Difficulty
Before diving into the details, it’s essential to recognize which specific aspects of the material are most difficult for you. Once you’ve pinpointed the tricky areas, you can devote more time to understanding them. Some common challenges might include:
- Complex Formulas: Formulas that involve multiple variables can be difficult to grasp. Try breaking them down into smaller, more manageable parts to see how each variable influences the result.
- Abstract Theories: Theoretical concepts can sometimes feel disconnected from practical applications. Relating these theories to real-world scenarios can make them more understandable.
- Multistep Problems: Problems that require multiple steps can be overwhelming. Focus on one step at a time, ensuring you understand each before moving on.
Approach Difficult Concepts Strategically
Once you’ve identified the challenging concepts, it’s time to apply some strategies to master them. Use these techniques to enhance your comprehension:
- Break Down the Problem: Decompose complicated ideas into smaller sections and tackle each piece individually. This makes it easier to absorb and retain information.
- Utilize Multiple Resources: If a particular explanation isn’t clear, look for alternative resources such as videos, textbooks, or online tutorials that may present the concept in a different way.
- Discuss with Peers or Teachers: Sometimes, a fresh perspective can help clarify things. Don’t hesitate to ask for help or engage in discussions with others who may have a clearer understanding.
By following these steps and consistently reviewing difficult concepts, you can transform challenging material into something more manageable. With practice and the right approach, you’ll develop a solid grasp of the material.
Common Pitfalls and How to Avoid Them
When solving complex problems, there are several common mistakes that can derail your progress. These pitfalls often stem from misinterpretation of the problem, poor calculation techniques, or overlooking key details. By being aware of these issues, you can take proactive steps to avoid them and improve the accuracy of your solutions.
- Rushing Through Problems: One of the most frequent mistakes is rushing through the steps without carefully reading the instructions or understanding the question. Always take your time to ensure you fully grasp the task at hand before starting.
- Skipping Steps: In an attempt to save time, it’s easy to skip intermediate steps in calculations or reasoning. This can lead to errors that are hard to spot later. Always document each step to track your work and ensure consistency.
- Overlooking Units and Conversions: Failing to pay attention to units of measurement or neglecting conversions can result in incorrect answers. Always double-check your units, especially when working with multiple systems of measurement.
- Misapplying Formulas: Applying a formula incorrectly is a common mistake, especially when multiple formulas are involved. Be sure to understand how each formula is derived and what variables it includes before using it in your solution.
Practical Tips for Avoiding Mistakes
Here are some practical strategies to help you avoid these pitfalls and ensure that your problem-solving approach is both accurate and efficient:
- Double-Check Your Work: Always review your steps before finalizing an answer. A quick check can often reveal overlooked mistakes.
- Take Breaks When Stuck: If you find yourself stuck on a problem, stepping away for a short time can help clear your mind and allow you to return with a fresh perspective.
- Use Visual Aids: Diagrams and charts can help clarify complex relationships and give you a clearer view of the problem, reducing the chance of errors.
- Practice Regularly: The more you practice, the more familiar you will become with common problem types and the steps needed to solve them. Repetition helps reinforce key concepts and reduce mistakes over time.
By being mindful of these common pitfalls and implementing strategies to avoid them, you’ll be better equipped to solve problems with confidence and accuracy.
Using Resources to Help with Answers
In any learning process, having access to the right tools and resources can significantly enhance your ability to solve problems effectively. Whether you’re tackling difficult concepts, verifying your solutions, or looking for additional explanations, there are various resources available to guide you. Utilizing these materials not only provides clarity but also strengthens your understanding of the subject matter.
Here are some valuable resources that can help improve your problem-solving skills:
| Resource | How It Helps |
|---|---|
| Textbooks and Guides | Provide step-by-step instructions, explanations, and examples to reinforce understanding and solve complex problems. |
| Online Tutorials | Offer video lessons and interactive exercises that break down difficult topics into manageable segments. |
| Study Groups | Allow you to collaborate with peers, discuss challenging concepts, and share problem-solving strategies. |
| Practice Problems | Give you the opportunity to apply learned techniques to a variety of scenarios, helping solidify your knowledge. |
| Expert Tutors | Offer personalized guidance to clarify concepts and provide insights into effective problem-solving techniques. |
By using these resources effectively, you can approach problems with a clearer perspective, reducing confusion and improving your overall performance. Regularly engaging with different materials allows you to gain deeper insights and refine your problem-solving approach.
Advanced Techniques for Chapter 2 Solutions
Mastering complex problem-solving often requires the application of advanced techniques that go beyond basic methods. These strategies enable deeper insight and more efficient approaches, helping to tackle challenging tasks with greater ease. By incorporating higher-level methods, you can solve problems more effectively and uncover patterns that simplify the process.
Techniques for Simplifying Complex Problems
One of the most powerful ways to approach difficult problems is by breaking them down into smaller, manageable parts. This method allows for clearer thinking and helps avoid feeling overwhelmed. In addition, recognizing key concepts and their relationships within a problem can lead to faster solutions. Below are some advanced techniques that can help refine your approach:
| Technique | Description |
|---|---|
| Divide and Conquer | Break the problem into smaller sections, solving each part individually before combining the results for the final solution. |
| Modeling and Visualization | Create visual representations, such as graphs or diagrams, to better understand the structure and dynamics of the problem. |
| Pattern Recognition | Look for recurring patterns or structures in problems to identify shortcuts or familiar techniques that simplify the process. |
| Approximation Techniques | Use estimation methods when an exact solution is difficult to obtain, reducing the complexity of the problem while maintaining accuracy. |
Maximizing Efficiency in Problem-Solving
Efficiency in solving advanced problems comes from knowing when and how to apply these techniques. Practice and familiarity with the subject matter help identify which methods work best for specific types of challenges. Developing a systematic approach, based on these techniques, will ensure quicker and more accurate solutions in the long run.
How to Build Confidence with Chapter 2

Building confidence when approaching challenging tasks requires a combination of practice, understanding, and perseverance. Gaining a strong grasp of key concepts and applying them step by step is essential to becoming more comfortable and effective. The more you engage with the material and practice solving problems, the more confident you will become in your ability to tackle complex issues.
Steps to Strengthen Your Confidence
To build confidence, it’s important to follow a structured approach that allows you to reinforce your understanding and master difficult concepts over time. Below are several steps you can take to boost your confidence:
- Start with the Basics – Begin by reviewing foundational principles. Ensure that you understand the core concepts before moving on to more complex problems.
- Practice Regularly – Consistency is key. The more problems you solve, the more confident you will become in applying your knowledge.
- Reflect on Mistakes – Mistakes are an opportunity to learn. Take time to analyze errors and understand where things went wrong, which will help you avoid similar pitfalls in the future.
- Seek Help When Needed – If you encounter roadblocks, don’t hesitate to seek assistance from peers, instructors, or resources. Collaborating with others can enhance your understanding and build your confidence.
- Celebrate Small Wins – Acknowledge your progress, even with small successes. This will motivate you to keep moving forward and help solidify your growing skills.
Maintaining Long-Term Confidence
As you continue to practice and apply your knowledge, your confidence will naturally grow. Keep challenging yourself with more difficult tasks and push beyond your comfort zone. Confidence is built over time through persistence and a positive mindset.
Why This Section Is Important
The second section of any study material often serves as a critical foundation for understanding more advanced topics. This part of the curriculum introduces essential concepts and problem-solving techniques that will be pivotal as you progress. Without a solid grasp of the material covered here, tackling more complex challenges later on may become significantly harder.
Understanding the core principles presented in this section is vital for developing the necessary skills to solve real-world problems efficiently. By mastering these concepts, learners gain the ability to approach future tasks with a clearer mindset and better preparation. This section builds the confidence and expertise required to excel in subsequent lessons and practical applications.
What to Do After Completing This Section
Once you’ve finished working through the material in this section, it’s important to take the time to review and reinforce your understanding. Reflect on the key concepts you’ve learned and ensure that you can apply them confidently to different problems. Revisiting challenging topics or reviewing your mistakes can help solidify your grasp of the material.
Next, consider applying your knowledge to new practice problems or real-life situations. This practical application will help you connect theory with practice and build your problem-solving abilities. Additionally, seeking out additional resources or collaborating with peers can provide further insight and allow for a deeper understanding of the topics covered.