
Preparing for the AP exams requires more than just memorizing formulas and procedures. It demands a solid understanding of key mathematical principles and the ability to apply them efficiently under timed conditions. This section focuses on reviewing important problem-solving techniques to help you navigate through the exam with confidence.
Familiarity with past test questions is crucial in building both knowledge and test-taking strategies. By reviewing old exam sections, students can become familiar with the structure of problems, improve their reasoning skills, and develop quicker approaches to solving them. This practice helps identify common problem types and areas that require extra attention.
Achieving success on the exam relies not only on knowing the material but also on understanding how to manage time effectively, prioritize questions, and avoid typical pitfalls. With the right preparation, even complex problems can become manageable, allowing you to demonstrate your full potential on exam day.
1993 AP Calculus AB Multiple Choice Answers
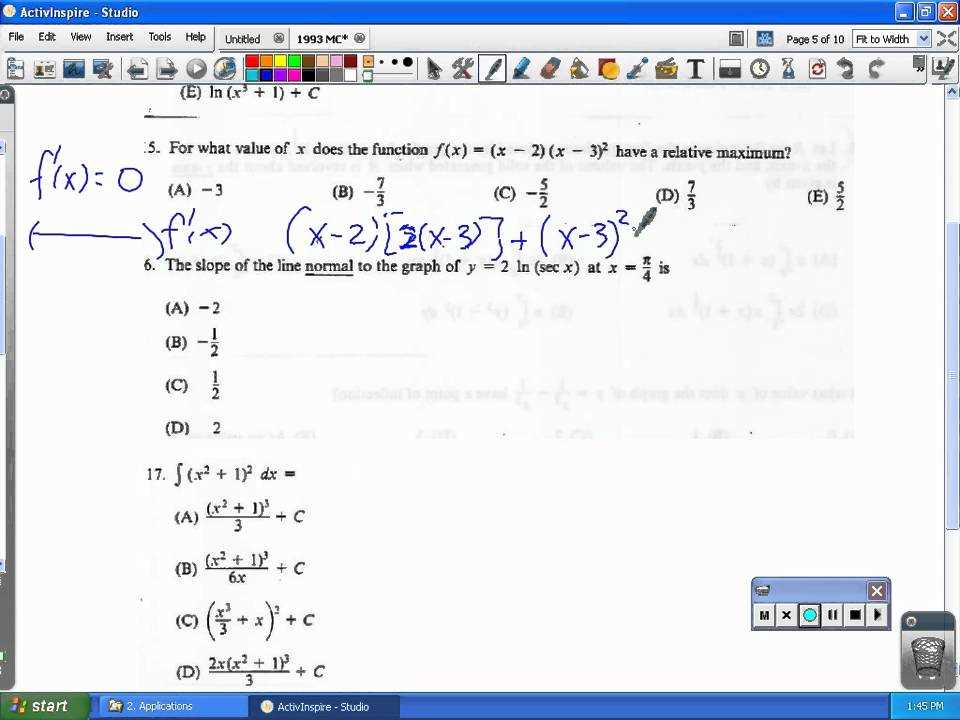
In this section, we will explore the solutions to the set of problems from the 1993 AP exam. These questions are designed to test a broad range of mathematical concepts, from fundamental principles to advanced problem-solving techniques. By reviewing the correct responses, students can gain valuable insights into the reasoning behind each solution and refine their approach to similar problems.
Each problem on the exam presents a unique challenge that requires both conceptual understanding and strategic thinking. By examining the correct options, it becomes easier to identify patterns and methods that can be applied to other questions in future tests. This process not only reinforces core knowledge but also enhances problem-solving skills, ensuring better performance on upcoming assessments.
Reviewing the solutions in this section will provide a clear picture of how to approach complex mathematical questions. Understanding why certain solutions are correct allows for a deeper grasp of the material, helping to avoid common mistakes and improving overall test-taking efficiency.
Overview of the 1993 AP Exam
The AP exam from this year was designed to evaluate students’ grasp of key mathematical concepts and their ability to apply these ideas in solving complex problems. It tested a variety of topics, assessing both theoretical knowledge and practical skills needed for success in higher education and beyond. The structure of the test aimed to challenge students’ understanding and critical thinking abilities in a timed environment.
Key Topics Covered
The exam focused on a wide array of topics, ranging from the basics of functions and derivatives to more advanced concepts such as integration and limits. The questions were crafted to test the depth of understanding in these areas, encouraging students to think critically and logically as they worked through each problem.
Test Format and Structure

The format of the test was designed to provide a comprehensive evaluation, with a mix of multiple question types. The questions required not only accurate calculations but also clear reasoning and efficient problem-solving strategies. Students were expected to apply their knowledge effectively within a limited timeframe.
Importance of Multiple Choice Questions
Questions with predefined options are an essential part of standardized exams, providing a unique method of assessment. These questions are designed to quickly gauge a student’s knowledge and ability to apply concepts effectively. They allow for a broad evaluation of various topics within a limited amount of time, offering both a challenge and a chance to demonstrate understanding.
Efficiency in Testing Knowledge
One of the key advantages of these types of questions is their ability to assess a wide range of material in a concise manner. By presenting several potential solutions, students are encouraged to carefully analyze each option before selecting the most accurate one. This process requires both depth of knowledge and careful attention to detail.
- They test broad concepts in a short time frame.
- They help evaluate recall and recognition skills.
- They reduce the impact of random guessing.
Improving Test-Taking Strategies
These questions not only evaluate knowledge but also enhance test-taking strategies. They encourage students to practice elimination techniques, develop a systematic approach to problem-solving, and manage time effectively during the exam. As students become familiar with the structure, they can increase their efficiency and performance on similar future exams.
- Practice with similar questions can increase speed.
- Time management skills are honed during practice.
- Understanding patterns in questions boosts confidence.
Key Topics Covered in the Exam
The exam was designed to test a wide range of mathematical principles, covering both foundational and advanced concepts. It emphasized understanding core ideas and the ability to apply them to solve complex problems. The topics addressed are essential for students aiming to demonstrate proficiency in various mathematical areas and provide a clear representation of their skills.
Functions and Their Properties were central to the exam, with many questions focusing on the behavior of different types of functions. Students needed to understand key concepts such as continuity, limits, and the properties that govern their transformations. A deep comprehension of these ideas is crucial for solving more advanced problems in the test.
Rates of Change also played a significant role, testing the ability to analyze and interpret how one quantity changes in relation to another. This involves understanding slopes, derivatives, and the application of these concepts to real-world situations. Mastery of these topics is essential for success in higher-level mathematics.
- Understanding the fundamental principles of limits.
- Interpreting derivatives and their real-world applications.
- Solving problems involving rates of change.
Another important area covered was integration techniques, which tested the student’s ability to compute areas, solve differential equations, and understand the relationship between differentiation and integration. This topic is foundational for further studies in mathematics and related fields.
Understanding the AP Calculus Format
The format of the AP exam is designed to test both the depth and breadth of students’ mathematical understanding. The structure aims to evaluate how well students can apply theoretical knowledge to practical scenarios, solve complex problems, and think critically under timed conditions. This section will break down the format, helping students understand what to expect and how to approach each part of the exam with confidence.
Structure of the Exam
The exam consists of two primary sections: one focused on solving problems with predefined responses and another requiring more in-depth written explanations. Both parts are designed to assess different skill sets, from basic calculations to the ability to justify mathematical reasoning. The exam emphasizes accuracy, efficiency, and clear problem-solving strategies.
- Section 1: Short-answer questions testing core skills.
- Section 2: Extended response questions requiring explanations and reasoning.
- Time management is crucial for success in both sections.
What to Expect During the Exam

During the test, students are expected to apply their knowledge quickly and accurately. The questions vary in difficulty, with some requiring simple computations, while others challenge students to integrate multiple concepts. Being familiar with the format and practicing under timed conditions can greatly improve test performance.
- Familiarize yourself with the question types.
- Focus on mastering both computational and reasoning skills.
- Practice managing your time effectively throughout the exam.
Strategies for Solving Multiple Choice
Approaching questions with predefined options requires a strategic mindset. Success depends not only on understanding the material but also on applying efficient problem-solving techniques. By focusing on eliminating incorrect choices, managing time wisely, and verifying work, students can increase their chances of selecting the correct response and improve their overall performance on the exam.
One effective strategy is to first read through all the options carefully and rule out the obviously incorrect ones. This narrows down the possibilities, making the selection process easier. If unsure about the answer, try to estimate the solution based on your understanding of the problem, and then choose the option closest to that estimate. Avoid spending too much time on any single question to ensure that there’s enough time for all questions.
| Strategy | Description |
|---|---|
| Eliminate Incorrect Answers | Identify and discard clearly wrong options to simplify decision-making. |
| Estimate the Solution | Use estimation to select the answer that seems closest to your expected result. |
| Check for Patterns | Look for patterns in the answers that may hint at the correct choice. |
| Manage Your Time | Don’t linger too long on a single question. Keep a steady pace throughout the test. |
Additionally, practicing with past exams and understanding the types of problems you may encounter helps build confidence and familiarity with the format. This preparation allows you to approach each question with clarity and reduce the chances of second-guessing your selections.
Common Mistakes to Avoid
When solving problems with predefined options, it’s easy to fall into certain traps that can lead to incorrect choices. Many students make simple errors due to rushing, misreading the question, or overlooking important details. Understanding and avoiding these common mistakes can significantly improve your performance and help you approach each problem more confidently.
Rushing Through Questions
One of the most common mistakes is rushing through questions without carefully considering each option. It’s essential to read the question thoroughly and take the time to analyze all possible answers before making a choice. Rushing can lead to overlooking critical details, such as sign errors or small nuances that might change the solution completely.
Overlooking Important Details
Another frequent error is missing key information in the problem itself. Many questions include subtle hints or constraints that are essential for finding the correct solution. Whether it’s a specific value or a condition that must be met, ignoring these details can result in the wrong answer. Always ensure that you have a clear understanding of the problem before making a decision.
- Double-check signs and calculations before selecting an answer.
- Make sure all conditions and constraints are understood before solving.
- Avoid jumping to conclusions based on incomplete information.
By being mindful of these common mistakes and taking a more careful, deliberate approach, you can avoid costly errors and improve your test-taking efficiency. Developing good habits, such as reviewing your work and checking for common pitfalls, can make a significant difference in your exam results.
How to Prepare for the Exam
Preparing for an exam with predefined response options requires both thorough study and strategic practice. Success comes not only from mastering the material but also from understanding the structure of the test and the most efficient ways to approach different question types. By developing a clear plan and practicing regularly, students can build confidence and improve their performance on exam day.
Study the Core Concepts
To begin, focus on the key concepts that are most likely to appear on the exam. This includes understanding fundamental principles, solving related problems, and reviewing any areas where you may feel less confident. Build a strong foundation by practicing various types of problems to solidify your understanding. Focus on the areas that are typically emphasized in past exams and exercises.
- Review essential mathematical principles and methods.
- Practice problem-solving regularly to reinforce concepts.
- Identify areas of weakness and spend extra time reviewing them.
Practice with Past Exams
Another critical part of preparing for the exam is practicing with past tests. This helps familiarize you with the format, time constraints, and types of questions you may encounter. It also allows you to develop test-taking strategies and become more comfortable with answering questions under pressure. Simulate real exam conditions to gauge your readiness and adjust your approach as needed.
- Work through previous exams to understand the test structure.
- Time yourself while taking practice tests to improve speed.
- Analyze incorrect answers to identify mistakes and improve.
By combining focused study with practice exams, you’ll be well-equipped to tackle the test with confidence. Preparation is key, and practicing under realistic conditions will help you refine your skills and improve your exam performance.
Using Past Exams for Practice
One of the most effective ways to prepare for an exam is by practicing with previous test papers. By working through past assessments, students can gain valuable insight into the types of questions they may face, understand the format of the test, and identify areas for improvement. This practice helps build familiarity with the content and the testing environment, ultimately boosting confidence and enhancing performance.
Reviewing past exams allows students to identify recurring themes and question patterns. This enables them to focus on specific areas where they are more likely to be tested. In addition, practicing with older exams helps students learn how to manage time effectively, ensuring they can complete all sections within the allotted time. Repetition through past papers also helps to reinforce key concepts, making them easier to recall on test day.
- Gain familiarity with the test format and structure.
- Identify recurring themes and common question types.
- Improve time management by simulating test conditions.
Moreover, reviewing your performance on past exams is crucial. After completing practice tests, it’s essential to go over your mistakes and understand why certain answers were incorrect. This reflection allows students to pinpoint weaknesses and adjust their approach to problem-solving, ensuring they are better prepared for the actual exam.
- Analyze each question and identify the reason for any incorrect answers.
- Focus on areas where you made mistakes and revisit those topics.
- Reattempt difficult questions to reinforce understanding and improve skills.
By consistently practicing with past exams and learning from mistakes, students can build the skills and confidence needed to succeed when facing the actual test.
Detailed Answer Key for 1993 Exam
Having access to a comprehensive answer key can significantly aid in the study process. It provides not only the correct solutions but also a detailed explanation of how each answer is derived. By reviewing each step, students can gain a deeper understanding of the reasoning behind the correct responses, which is crucial for mastering similar problems in the future.
In this section, we break down the solutions to each question from the exam, offering clear, step-by-step explanations. This method of analysis helps identify common problem-solving techniques and strategies that can be applied across various types of questions. It’s important to note that understanding the rationale behind each correct response is just as valuable as knowing the final answer.
- Step-by-Step Solution Breakdown: For each question, we provide a thorough explanation of the approach used to find the correct solution.
- Understanding Common Errors: We highlight common mistakes that students make and explain how to avoid them in the future.
- Reinforcing Key Concepts: Each explanation reinforces fundamental principles that are frequently tested, aiding in overall comprehension.
By examining the answer key in detail, students can refine their problem-solving abilities and enhance their understanding of key concepts. The goal is not only to arrive at the correct answers but also to gain insight into the thought process that leads to those solutions, which can prove invaluable for future exams.
Interpreting the Answer Key Results
After reviewing the results from the answer key, it’s essential to go beyond simply identifying which answers were correct or incorrect. Understanding the reasoning behind each solution helps students grasp the underlying concepts, which is crucial for improving their problem-solving skills. By analyzing the explanations, students can pinpoint areas of strength and areas that require further practice.
Each answer key provides more than just a final solution; it offers an opportunity to reflect on how the correct answer was derived. For example, certain questions might involve specific strategies, formulas, or concepts that students need to apply. By examining these methods in detail, students can improve their approach to similar problems in future assessments.
- Identify Patterns: Look for recurring strategies or techniques that appear in multiple questions to better recognize problem types.
- Learn from Mistakes: Pay special attention to incorrect answers to understand why certain approaches were ineffective and how to avoid them.
- Reinforce Core Concepts: Review the explanations for each solution to reinforce your understanding of fundamental principles.
Interpreting the results of an answer key goes beyond checking your work. It’s about learning from both correct and incorrect solutions, strengthening your understanding of key concepts, and building the skills necessary to perform better in future assessments. By reflecting on each step, you’ll develop a deeper understanding of the subject and become more adept at handling similar challenges moving forward.
Reviewing Critical Mathematical Concepts
Mastering the essential concepts in mathematics is key to performing well on any exam. In this section, we focus on the foundational ideas that are frequently tested, ensuring a solid understanding of the critical principles. By revisiting these concepts, students can reinforce their knowledge and improve their ability to tackle similar problems in future assessments.
When preparing for exams, it’s crucial to revisit core ideas that underpin many questions. These include fundamental theories, key operations, and common techniques that are often tested in various problem-solving scenarios. A strong grasp of these core concepts not only helps with solving specific questions but also builds a deeper understanding of the subject as a whole.
Key Topics to Focus On
- Derivatives and Rates of Change: Understanding how to find the rate of change of a function is central to many questions.
- Integration Techniques: Review various methods of integration, such as substitution and integration by parts, which are often tested in different contexts.
- Limits and Continuity: A solid understanding of limits and their role in defining continuity is crucial for many fundamental problems.
- Optimization Problems: Learn how to set up and solve problems that require finding maximum and minimum values of functions.
Common Mistakes to Avoid
- Failing to properly apply the chain rule when differentiating complex functions.
- Misunderstanding the concept of definite vs. indefinite integrals.
- Ignoring the conditions required for continuity when solving limits.
- Rushing through word problems without carefully analyzing all given information.
Reviewing these critical concepts will help solidify your understanding and increase your confidence. By recognizing the key areas that are frequently tested, you can better prepare for the challenges presented in mathematical assessments. Consistent practice with these topics will enhance problem-solving skills and prepare you to tackle a variety of question types with ease.
How to Improve Your Test Scores
Improving your test performance requires a strategic approach that combines solid preparation, effective time management, and a clear understanding of the material. By focusing on key areas of improvement, you can boost your confidence and increase your chances of achieving better results. This section highlights proven strategies to enhance your test scores and achieve your academic goals.
The process of improving your results starts with mastering the material. However, it’s also essential to adopt effective study habits, practice regularly, and simulate test conditions to get the best outcome. Knowing how to approach different types of questions and managing your time effectively during the exam can significantly impact your performance.
Effective Strategies for Test Improvement
| Strategy | Description |
|---|---|
| Consistent Practice | Regularly solving problems and reviewing concepts will help reinforce your understanding and make problem-solving quicker during the exam. |
| Simulate Test Conditions | Take practice exams under timed conditions to improve your ability to manage time and adapt to the pressure of a real test. |
| Analyze Mistakes | Carefully review the errors you make to understand why they happened and avoid them in the future. |
| Focus on Weak Areas | Identify the concepts that you struggle with the most and devote extra study time to mastering those areas. |
| Time Management | Learn how to allocate time efficiently between different sections of the test to avoid rushing through questions. |
By incorporating these strategies into your study routine, you will gradually build the skills needed to improve your test scores. Focusing on consistent practice, learning from your mistakes, and refining your test-taking techniques will not only enhance your academic performance but also help you approach exams with greater confidence and clarity.
Time Management During the Exam
Effective time management is a crucial skill for maximizing your performance on any test. With limited time and a variety of questions to answer, it is essential to develop a strategy that ensures you allocate sufficient time to each section while avoiding unnecessary delays. By managing your time wisely, you can approach the exam with a calm and organized mindset, increasing your chances of success.
One of the key elements in time management is understanding the structure of the test and the time available for each part. Prioritize questions based on difficulty and familiarity, and avoid spending too much time on any single problem. With the right approach, you can efficiently move through the test while ensuring you give each question the attention it requires.
Time Allocation Tips

1. Break Down the Exam – Before you start, quickly review the entire test to determine how much time you should allocate to each section. Divide your total time by the number of sections or questions to get an approximate amount of time to spend per task.
2. Start with Easier Questions – Begin with questions you are confident about. This will help build momentum and give you extra time to focus on more challenging problems later on.
Techniques to Avoid Time Wastage
1. Don’t Get Stuck – If you encounter a question that is taking too long, move on and return to it later if time permits. It’s important to keep the flow of the exam going.
2. Monitor the Clock – Keep an eye on the time as you progress. Set a mental checkpoint to gauge whether you are on track to finish all sections.
By applying these strategies, you can ensure that your time is used efficiently throughout the exam. Proper time management will not only help you complete the test but also reduce stress and allow you to focus on the most important tasks at hand.
Tips for Advanced Problem Solving
When tackling complex questions, it’s essential to approach the problem strategically. Advanced problems often require a deeper understanding of the subject matter and the ability to apply various techniques efficiently. The key is to break down the problem into manageable parts and recognize patterns or strategies that lead to solutions.
To enhance your problem-solving skills, focus on developing a structured approach. By utilizing specific strategies and refining your methodical thinking, you can improve your ability to tackle even the most challenging questions.
Effective Approaches to Complex Problems

- Understand the Problem – Before jumping into calculations, take the time to read the question carefully. Identify what is being asked and what information is provided. This will guide your approach and prevent mistakes.
- Break Down the Problem – Divide the problem into smaller, simpler steps. This makes it easier to identify a solution path and reduces the likelihood of feeling overwhelmed.
- Look for Patterns – Many advanced problems share similar structures. Try to recognize patterns from previous problems or exercises that might help simplify the task at hand.
- Work Backwards – In some cases, it may be helpful to start from the desired outcome and work backward. This approach can offer insights into the steps needed to reach the solution.
Maximizing Efficiency with Techniques
- Use Known Formulas – Whenever possible, apply formulas and theorems that are relevant to the problem. Familiarity with key concepts will save time and increase accuracy.
- Eliminate Wrong Choices – If the problem involves selecting an option from a list, eliminate choices that are clearly incorrect. This will increase your chances of selecting the correct answer even when unsure.
- Check Your Work – After completing the problem, quickly review your solution to ensure there are no calculation errors or missed steps. This helps catch simple mistakes that could cost you valuable points.
By practicing these strategies and refining your problem-solving skills, you can improve your ability to handle complex questions efficiently and accurately. Continuous practice and a thoughtful approach will lead to greater confidence when faced with difficult challenges.
Utilizing Online Resources Effectively
The internet offers a vast array of tools and platforms that can significantly enhance your preparation for exams. With the right resources, you can access practice materials, tutorials, and expert advice that will help strengthen your understanding and problem-solving abilities. However, it’s important to use these resources strategically to maximize their benefits and avoid distractions.
By carefully selecting the most relevant online platforms and maintaining a disciplined study routine, you can improve your knowledge and increase your chances of success. Below are several key strategies for using online tools effectively.
Key Online Resources for Exam Preparation
- Practice Websites – Many websites offer practice tests and quizzes that simulate the structure of real exams. These tools can help familiarize you with the format and timing of the test, allowing you to assess your strengths and areas for improvement.
- Video Tutorials – Platforms like YouTube feature countless tutorial videos created by experienced educators. These resources can be particularly useful for visual learners and for topics that require detailed explanations.
- Interactive Learning Platforms – Websites that offer interactive exercises, such as quizzes and problem-solving simulations, can be very beneficial. These platforms often provide immediate feedback, which helps reinforce concepts and identify mistakes in real-time.
- Study Groups and Forums – Engaging in online discussions with peers can provide new perspectives and help clarify difficult concepts. Forums and study groups allow you to ask questions and share insights with others who are also preparing for the exam.
Maximizing the Benefits of Online Tools

- Set Clear Goals – Before using any online resource, define what you aim to achieve. Whether it’s mastering a specific topic or practicing timed questions, setting goals will help you stay focused and make your use of online resources more productive.
- Use Reputable Sources – While there are many online tools available, not all of them are trustworthy or effective. Make sure to use established platforms and websites that are recognized for providing accurate and high-quality materials.
- Stay Organized – With so many resources available, it’s easy to get overwhelmed. Create a study plan that incorporates various online tools in a structured way, so you can make the most of your study sessions without wasting time.
- Balance Screen Time – While online resources can be very helpful, it’s important to balance your screen time with other study methods. Taking breaks and engaging with physical materials can help maintain focus and prevent burnout.
When used effectively, online resources can complement your traditional study methods and give you access to valuable practice and insights. By selecting the right tools and using them efficiently, you can boost your readiness and increase your confidence heading into the exam.
Practice with Previous Exam Questions
One of the most effective strategies for improving your performance in any test is to practice with questions from past exams. By doing so, you become familiar with the format and types of problems that are typically asked, as well as the level of difficulty you can expect. Additionally, this practice helps reinforce key concepts and sharpen problem-solving skills, which are crucial for success.
Working through old exam questions also provides insight into the structure of the test, how questions are framed, and the time constraints you will face. This allows you to develop strategies for managing time during the actual exam and helps build your confidence.
Benefits of Practicing with Past Questions
- Familiarity with Question Patterns: Repeated exposure to various question types will help you recognize patterns and improve your ability to quickly identify the correct approach to solving problems.
- Enhanced Problem-Solving Skills: By practicing problems that are representative of what you’ll encounter on the exam, you’ll refine your problem-solving techniques and become more efficient at tackling complex questions.
- Time Management: Practicing under exam-like conditions will help you get accustomed to the time limits, allowing you to pace yourself during the actual test.
- Review of Key Concepts: Reviewing past questions allows you to revisit important topics, ensuring that you reinforce your understanding of critical concepts.
How to Effectively Use Past Exam Questions

- Start with Easy Questions: Begin by working through questions you are already familiar with to build your confidence. Gradually move to more challenging questions as your comfort level increases.
- Simulate Exam Conditions: Try to replicate the conditions of the actual exam by timing yourself and avoiding distractions while working on past questions.
- Review Mistakes: After attempting each set of questions, review your answers, especially the incorrect ones. Understand where you went wrong and identify areas for improvement.
- Focus on Weak Areas: If certain topics or question types consistently cause difficulty, prioritize those areas in your study sessions and seek additional practice for them.
Example Table of Past Questions
| Topic | Question Type | Difficulty Level |
|---|---|---|
| Limits and Continuity | Direct Calculation | Moderate |
| Derivatives | Application Problem | Challenging |
| Integrals | Definite Integration | Moderate |
| Series Expansion | Theoretical Proof | Advanced |
Practicing with questions from previous exams is an excellent way to prepare for your upcoming test. Not only does it familiarize you with the format, but it also helps you to refine your test-taking skills and improve your overall performance. The more you practice, the more confident you’ll feel on exam day.
Final Preparation for AP Calculus

The final stretch before any major exam is crucial for consolidating knowledge and boosting confidence. This period is your chance to refine your understanding, clarify any lingering doubts, and ensure you’re fully prepared for the test. A strategic and well-organized approach during this time can make a significant difference in your performance.
As the exam date approaches, it’s important to focus on reviewing key concepts, practicing problem-solving techniques, and managing stress effectively. By following a structured study plan, you can maximize your chances of achieving your desired score.
Effective Review Strategies
- Prioritize Weak Areas: Identify topics where you’re struggling the most and dedicate more time to mastering them. Whether it’s integration, limits, or series, target your weaknesses to improve overall understanding.
- Review Past Mistakes: Go through previous practice tests or homework and carefully analyze any mistakes. Understand why the correct answer is right and why you missed the mark. This helps reinforce concepts and avoid repeating errors.
- Summarize Key Concepts: Create summary notes for the major concepts and formulas. Having a concise, organized set of notes to review can help solidify your memory and boost confidence.
Practice Under Exam Conditions
- Time Yourself: Practice answering questions under strict time limits. This will help you get accustomed to the pressure and manage time effectively during the actual exam.
- Simulate Real Test Scenarios: Create mock exams by choosing a set of questions and completing them without any distractions. This simulates the real exam environment and can help reduce anxiety.
- Focus on Efficiency: Work on finding quicker ways to solve problems without sacrificing accuracy. Look for shortcuts or techniques that can help you save time while still arriving at the correct solution.
Test Day Preparation
- Get Plenty of Rest: A well-rested mind performs better. Ensure you get a good night’s sleep before the test to stay alert and focused.
- Stay Calm: Anxiety can be a major hindrance on test day. Practice breathing exercises or other relaxation techniques to keep calm and clear-headed.
- Double-Check Materials: The night before the test, ensure you have all the necessary materials ready–calculator, pencils, identification, and any required documentation. Having everything prepared reduces stress on the day of the exam.
With these final preparation steps, you’ll be ready to approach the exam with confidence and poise. The key is to stay focused, manage your time effectively, and ensure that you’re calm and collected when it’s time to perform. Remember, thorough preparation is the foundation for success, and with the right mindset, you can excel.