Preparing for advanced mathematics exams requires both strategic study and a strong understanding of the key concepts involved. Reviewing past tests can significantly enhance your problem-solving abilities and give you insight into the types of questions that are typically asked. This section focuses on providing a detailed analysis of one such exam, offering solutions and explanations for each problem encountered.
Through examining these questions and their corresponding solutions, you will gain a clearer perspective on how to approach similar challenges. In particular, the solutions will demonstrate effective techniques for breaking down complex problems and efficiently identifying the correct approaches. Whether you are preparing for a future test or seeking to sharpen your mathematical skills, this resource is designed to support your success.
Understanding past exam patterns and recognizing common question types are crucial steps in developing confidence and mastery over the subject matter. By working through this content, you will not only reinforce your knowledge but also refine your exam-taking strategies.
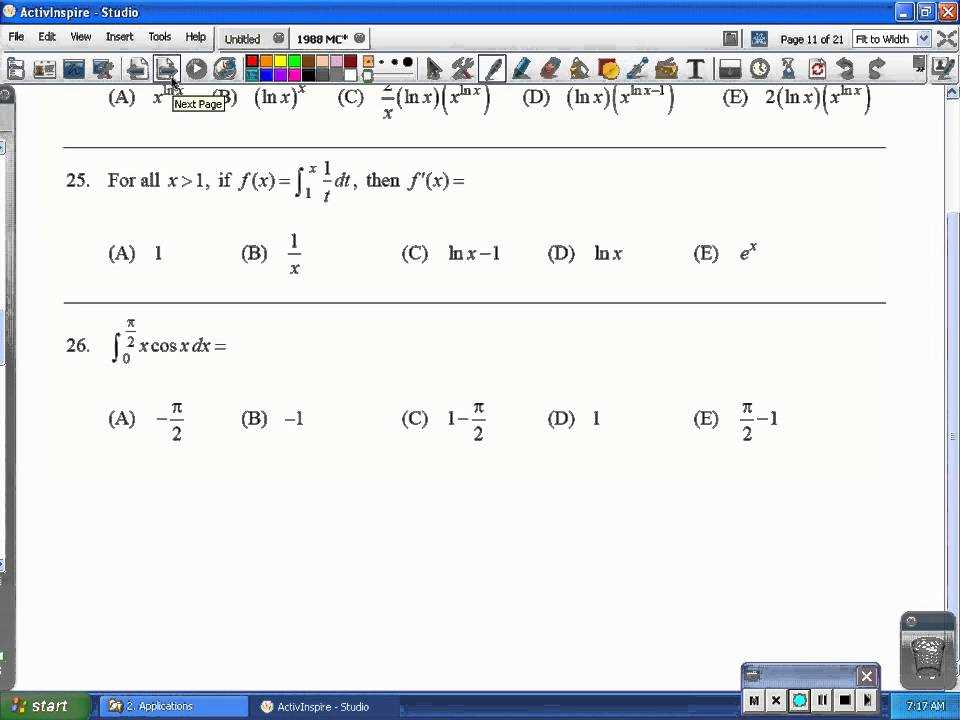
1988 AP Calculus BC Multiple Choice Answers
This section provides a comprehensive look at the solutions to a series of questions from a past advanced mathematics exam. It aims to help students understand the methodology behind each solution, breaking down the reasoning and techniques used to arrive at the correct responses. By reviewing these solutions, learners can enhance their problem-solving skills and become more adept at tackling similar challenges in future assessments.
Each question is accompanied by a clear explanation, illustrating the key concepts and strategies that lead to the correct outcome. The goal is to reinforce essential mathematical principles and improve your ability to apply them effectively in exam settings. Whether you’re preparing for an upcoming test or reviewing past material, this section serves as a valuable tool for honing your skills.
By working through these solutions, you’ll also become familiar with common question formats and the types of problems that often appear on exams of this nature. This insight will not only improve your test-taking efficiency but also deepen your understanding of the underlying mathematical theories that drive these questions.
Overview of the 1988 AP Calculus Exam
This section provides a detailed review of the structure and content of a past advanced mathematics exam, aimed at helping students understand the types of questions and the overall format. The exam assesses a broad range of mathematical concepts, testing both theoretical knowledge and practical application. Understanding the layout and style of the exam is essential for effective preparation and success in future assessments.
Structure and Format of the Exam
The exam typically consists of two major sections: one focused on multiple problems that test a wide range of topics, and another dedicated to longer, more complex questions requiring in-depth reasoning and analysis. Below is a breakdown of the exam components:
| Section | Description | Time Allotted |
|---|---|---|
| Section 1 | Multiple choice questions covering various topics | 45 minutes |
| Section 2 | Free response questions requiring detailed solutions | 90 minutes |
Topics Covered in the Exam
Throughout the exam, a variety of key mathematical areas are tested. These may include limits, differentiation, integration, and the application of these concepts to real-world problems. Mastery of these areas is crucial for performing well, as the questions are designed to assess both understanding and the ability to apply knowledge effectively.
How to Approach AP Calculus BC Questions
When preparing for advanced mathematics exams, understanding how to effectively tackle each question is key to performing well. By developing a clear strategy and mastering fundamental techniques, students can confidently approach problems, no matter how complex they may seem. The following approaches are designed to help you navigate through the different types of questions typically found in these assessments.
The first step is to read each question carefully and identify the specific concept being tested. Whether it’s a problem focused on differentiation, integration, or an applied scenario, recognizing the underlying mathematical principle is crucial. Once the concept is identified, break the problem into smaller, manageable parts and solve each one step by step.
Time management is also essential. While it’s important to be thorough, it’s equally important not to get stuck on a single problem. If a question feels particularly difficult, move on to the next one and return later if time allows. Practicing this approach helps build the ability to stay focused and work efficiently under exam conditions.
Finally, reviewing previous problems and solutions can significantly improve your speed and accuracy. Familiarity with problem types, as well as common techniques for solving them, allows you to quickly recognize patterns and apply solutions effectively. This combination of strategy, practice, and time management is key to mastering advanced mathematics exams.
Key Concepts Tested in 1988 Exam
This section highlights the core mathematical principles that were assessed in a past advanced mathematics exam. The questions were designed to evaluate students’ understanding of fundamental theories and their ability to apply these concepts in various problem-solving contexts. The concepts tested cover a wide range of topics, each requiring both analytical thinking and practical application skills.
Among the key areas examined were limits, derivatives, integrals, and series. These topics are central to higher-level mathematics and are critical for solving complex problems. For example, understanding how to find the rate of change in a given function or calculating the area under a curve were essential skills tested throughout the exam.
Additionally, the exam also included questions related to the application of these concepts in real-world scenarios. These types of problems required students to not only perform mathematical operations but also interpret results and apply their knowledge to practical situations, such as optimizing functions or analyzing motion.
Understanding the Multiple Choice Format
The structure of certain exam sections is designed to test a student’s ability to select the correct solution from a set of given options. These questions typically assess a broad range of topics in a concise format, allowing for efficient evaluation of knowledge and problem-solving abilities. While the format may appear straightforward, it requires careful attention to detail and a strategic approach to ensure accurate selections.
Each question presents a scenario followed by a set of possible answers. While some options may seem plausible, only one of them is correct. To approach these problems effectively, it is important to first eliminate any obviously incorrect choices. This technique, known as the process of elimination, can significantly increase the likelihood of selecting the correct answer even when the question appears challenging.
Critical thinking and familiarity with the material are essential in this format. Often, the questions are designed to test not just rote memorization but the application of concepts in different contexts. Therefore, reviewing common problem types and practicing similar questions can help you identify patterns and enhance your speed and accuracy during the exam.
Tips for Maximizing Your Score
Achieving a high score on advanced exams requires more than just knowing the material–it involves strategic preparation and efficient exam-taking techniques. The following tips will help you maximize your performance by focusing on effective study habits, time management, and problem-solving strategies. By honing these skills, you can approach the test with confidence and improve your results.
Effective Study Strategies
To excel on the exam, it’s essential to review key concepts and practice solving problems regularly. Here are some useful study techniques:
- Focus on Weak Areas: Identify topics that are more challenging and dedicate extra time to mastering them.
- Practice with Past Exams: Reviewing previous tests allows you to become familiar with the question formats and common problem types.
- Use Study Aids: Textbooks, online resources, and study groups can provide additional support and explanations for difficult concepts.
- Time Your Practice Sessions: Simulating exam conditions by timing your practice sessions can help improve your pacing and focus during the actual test.
Test-Taking Strategies
Once you’re in the exam room, implementing the right strategies can make a significant difference in your score. Here are some key approaches to keep in mind:
- Start with Easy Questions: Begin by answering the questions you’re most confident about. This boosts your morale and ensures you accumulate points early on.
- Don’t Get Stuck: If you encounter a difficult question, move on and return to it later. This prevents wasting time on one problem.
- Eliminate Incorrect Options: Narrow down the possible answers by eliminating clearly wrong options. This increases your chances of selecting the right answer even if you’re unsure.
- Check Your Work: If time allows, review your answers to ensure that you’ve correctly solved each problem and answered as accurately as possible.
Answer Breakdown for 1988 Exam
Understanding how to approach and solve each question is crucial for achieving a high score on an advanced mathematics exam. This section provides a detailed breakdown of the solutions for each problem from the exam, highlighting the methods used to reach the correct results. By following the step-by-step process for each question, you can gain insight into the reasoning behind the answers and improve your problem-solving abilities for similar questions in the future.
Step-by-Step Solution Analysis
The key to mastering exam questions lies in recognizing the appropriate methods to apply in different scenarios. Here’s an analysis of how to approach various types of problems in the exam:
- Problem 1: The first question tests basic understanding of the fundamental concepts. Begin by identifying the variables and applying known formulas to simplify the expression. A clear understanding of basic principles is essential for solving this type of problem.
- Problem 2: This problem focuses on more complex operations. Break it down into smaller steps and use elimination strategies to rule out incorrect options. Practice with similar problems helps improve speed and accuracy in solving this kind of question.
- Problem 3: Here, the focus is on applying theoretical knowledge to real-world scenarios. Recognize the type of application and approach it by applying the relevant formulas. Don’t forget to check units and final results to ensure consistency.
Common Mistakes to Avoid
While solving exam questions, certain errors tend to occur frequently. Being aware of these common pitfalls can help you avoid them and improve your accuracy:
- Overlooking Key Information: Ensure you carefully read all parts of the question, as important details can sometimes be hidden within the wording.
- Skipping Steps: While time pressure can be a factor, skipping steps in the solution process can lead to mistakes. Always follow the necessary procedures, even if the problem seems simple.
- Misinterpreting Results: Pay close attention to the units or specific conditions required by the problem. Misinterpretation can lead to incorrect conclusions and answers.
Common Mistakes on the 1988 AP Test
During any advanced mathematics exam, students often fall into specific traps that can negatively impact their scores. Identifying these common mistakes and learning how to avoid them is essential for success. This section outlines some of the most frequent errors made during the test and offers guidance on how to prevent them, ensuring a more efficient and accurate approach to each problem.
Rushing Through Problems
One of the most common mistakes students make is rushing through the questions, especially when they feel pressed for time. While it’s important to manage time efficiently, skipping steps or not double-checking calculations can lead to careless errors.
- Missed Calculations: Small arithmetic mistakes can add up, leading to incorrect results. Always take time to check intermediate steps before finalizing answers.
- Ignoring Units: Failing to keep track of units, especially in applied problems, is another common pitfall. Ensure that units are consistent throughout the problem.
- Inaccurate Interpretations: Misunderstanding the question or the way data is presented can lead to applying the wrong method. Always read questions carefully, ensuring you understand exactly what is being asked.
Overlooking Key Information
Many students overlook important details or assumptions that are stated in the problem. These overlooked points can often make the difference between the correct and incorrect solutions.
- Unnoticed Conditions: Problems may contain assumptions such as specific constraints or ranges for variables that must be considered when solving the problem. Missing these can lead to incomplete or incorrect solutions.
- Misinterpreting Graphs: Graphs and visual representations often contain critical information that is easy to overlook. Be sure to analyze them carefully and check the scales, labels, and any given points.
Strategies for Solving Calculus Problems
Approaching advanced mathematical problems requires a blend of theoretical knowledge and practical problem-solving skills. Developing effective strategies can help you navigate complex questions more efficiently and with greater accuracy. This section explores key strategies for tackling problems typically found in these types of exams, helping you build a structured approach to finding solutions.
Step-by-Step Problem Solving
Breaking down each problem into manageable steps is one of the most effective strategies. By following a systematic process, you ensure that you don’t miss crucial details and can stay focused on the task at hand.
- Understand the Problem: Before jumping into calculations, take a moment to carefully read the question and identify what is being asked. Recognize the key information and determine the variables involved.
- Choose the Right Approach: Based on the type of problem, decide which method to use. Whether it’s a derivative, an integral, or a limit, knowing the appropriate technique is essential.
- Work Step by Step: Avoid skipping intermediate steps. This will help you stay organized and reduce the risk of making errors during calculations.
Time Management Techniques
Managing your time efficiently during the exam is crucial. Being able to prioritize questions and allocate time appropriately can help you complete the test with fewer mistakes.
- Start with Familiar Problems: Begin with questions that you find easier or are most confident about. This will build momentum and save time for the more difficult questions.
- Don’t Get Stuck: If you encounter a particularly challenging question, move on to the next one and return to it later if time permits. This helps prevent getting bogged down by a single problem.
- Allocate Time for Review: Reserve a few minutes at the end to review your answers. Check for calculation mistakes or misunderstood questions that could affect your score.
Reviewing Past Exam Questions for Success
One of the most effective ways to prepare for an advanced mathematics exam is by reviewing previous exam questions. By analyzing past problems, you not only familiarize yourself with the types of questions that may appear, but also develop strategies for tackling similar challenges. This section discusses how revisiting past exams can help reinforce key concepts and improve problem-solving skills, setting you up for success in your own exam.
Benefits of Reviewing Past Questions
Revisiting old exam questions offers several advantages. It allows you to see the kinds of problems that are commonly tested, recognize patterns in question formats, and identify areas where you may need additional practice.
- Understanding Question Patterns: Past exams often repeat certain question structures or themes. Recognizing these patterns can help you anticipate what to expect in your own test.
- Improving Speed and Accuracy: The more you practice, the more efficient and accurate you become at solving problems. Familiarity with problem types allows you to work through them more quickly and with greater precision.
- Strengthening Conceptual Understanding: By solving various problems, you reinforce your understanding of the underlying concepts, making it easier to apply them when faced with new challenges.
How to Effectively Use Past Exam Questions
To make the most of your review, it’s important to approach past exams strategically. Simply solving the problems isn’t enough – it’s essential to analyze the solutions and understand why certain methods work best for each problem.
- Review Solutions Carefully: After solving a problem, compare your solution with the correct one. Pay attention to any differences in approach and consider how you can improve your method for future questions.
- Identify Weak Areas: If you struggle with certain types of questions, dedicate additional time to those topics. Practice similar problems until you feel confident in your ability to handle them on exam day.
- Simulate Exam Conditions: When working through past questions, try to simulate the time constraints of the actual exam. This will help you get used to managing your time effectively under pressure.
Sample Problem Breakdown
Here’s an example of how to analyze and solve a past exam problem:
| Problem | Method | Solution |
|---|---|---|
| Example Question 1 | Identify key concepts, apply relevant formula | Final answer with explanation |
| Example Question 2 | Break down into smaller steps, simplify expression | Final answer with explanation |
How to Use This Answer Key Effectively
Utilizing an answer key is a crucial part of the review process, but it’s important to approach it strategically. Simply comparing your answers to the provided solutions isn’t enough. A thoughtful review of both the correct and incorrect solutions allows for deeper understanding and helps you refine your problem-solving methods. This section explains how to make the most of an answer key to enhance your preparation and improve performance on exams.
Step-by-Step Review Process
Using an answer key effectively involves more than just checking if your answers are correct. It’s essential to understand the reasoning behind each solution and identify any mistakes in your approach. Follow this process for a comprehensive review:
- Check Your Work: Compare your solutions with the answer key. Identify whether your answer matches and where any discrepancies arise.
- Understand the Solution: Read through the solution carefully. Pay attention to the steps taken, the formulas used, and any techniques that might be new to you.
- Analyze Mistakes: If your answer is incorrect, figure out where you went wrong. Did you misunderstand the question, make a calculation error, or apply the wrong method? Understanding your mistakes is crucial for improving.
Enhancing Problem-Solving Skills
While the answer key provides the correct solutions, it’s important to view it as a learning tool that can help you develop more efficient problem-solving techniques. By studying the solutions in depth, you can improve your approach to similar questions in the future.
- Learn New Techniques: Sometimes the answer key may introduce new strategies or shortcuts. Take note of these methods and incorporate them into your future practice.
- Rework Problems: After reviewing the solutions, try solving the problems again on your own. This reinforces your understanding and ensures that you grasp the concepts.
- Focus on Patterns: Look for patterns in the solutions. Often, certain types of problems require similar approaches. Recognizing these patterns can save time during exams.
Sample Answer Key Breakdown
Here’s an example of how to break down the solution from the answer key:
| Problem | Your Approach | Correct Method | Key Takeaways |
|---|---|---|---|
| Example Question 1 | Incorrect approach, missed a step | Used correct formula, restructured steps | Focus on correct step order |
| Example Question 2 | Correct but rushed calculation | Careful with simplification | Take extra time on complex steps |
Importance of Practice in Calculus
Mastering complex mathematical concepts requires more than just understanding the theory behind them. To truly grasp the material and perform well on exams, consistent practice is essential. Engaging with a variety of problems helps solidify key concepts, build problem-solving skills, and boosts confidence. This section will highlight the importance of regular practice and how it directly impacts success on tests and long-term comprehension.
Why Practice Matters
Repetition is a crucial factor in reinforcing learning. When you practice regularly, you not only enhance your ability to solve problems more efficiently but also improve your ability to recognize patterns and apply appropriate methods. Here are several reasons why practice is so vital:
- Strengthens Understanding: Repeated exposure to different problem types helps you internalize formulas and concepts, making them easier to recall during exams.
- Builds Speed: Regular practice allows you to solve problems faster, which is particularly important when facing timed exams.
- Increases Accuracy: The more problems you work through, the more familiar you become with potential pitfalls, reducing the likelihood of mistakes.
Effective Practice Techniques
Not all practice is equal. To get the most out of your study time, it’s important to approach your practice sessions strategically. Below are some effective techniques:
- Start with Fundamentals: Begin by mastering the basic principles. As you become more comfortable, gradually move on to more complex problems.
- Diversify Problem Types: Practice a wide variety of problems to ensure you’re prepared for different scenarios. This will help you recognize similar questions on the actual test.
- Time Yourself: Practice solving problems under timed conditions to simulate the pressure of an actual exam.
- Review Mistakes: After practicing, always review the mistakes you made. Understanding why you got something wrong is just as important as knowing what you did right.
Tracking Progress
Regularly assessing your progress is also crucial. Keeping track of which topics you’re excelling in and which ones need more work allows you to focus your practice on areas that need improvement. Consider the following approaches to monitor your growth:
- Set Goals: Set specific targets for the number of problems you want to solve each week or for mastering particular topics.
- Track Time: Record how long it takes you to solve problems, and aim to improve your efficiency over time.
- Seek Feedback: Discuss difficult problems with peers or instructors to get a different perspective and gain deeper insights.
Real-World Applications of Calculus Concepts
Mathematics extends far beyond the classroom, playing a vital role in various fields of study and industries. The concepts learned in advanced math are not only theoretical but have practical applications that impact everyday life. In this section, we will explore how the principles studied in this area of mathematics are used in real-world situations, from engineering to economics and beyond.
Applications in Engineering and Physics
In the field of engineering, mathematical principles are the foundation of design, optimization, and problem-solving. Here’s how these concepts are utilized:
- Structural Analysis: Engineers use mathematical models to analyze forces acting on structures such as bridges, buildings, and dams. By calculating the distribution of forces and moments, they can ensure safety and stability.
- Motion and Velocity: In physics, the relationship between distance, velocity, and acceleration is studied using the concept of derivatives. This helps in designing vehicles, aircraft, and even space exploration technologies.
- Fluid Dynamics: Calculus is used to model the behavior of fluids in motion, helping engineers design systems like water pipes, air conditioning units, and even hydraulic machines.
Applications in Economics and Business
In economics, calculus is indispensable for modeling and optimizing financial systems, production processes, and market behavior. Here are a few key applications:
- Cost and Revenue Optimization: By applying derivatives, businesses can find the point of maximum profit by analyzing how costs and revenues change with varying production levels.
- Economic Growth Models: Calculus helps economists model and predict economic trends, allowing for better planning in terms of investments, resources, and policies.
- Supply and Demand Analysis: Economists use calculus to evaluate the effects of price changes on supply and demand, helping businesses set optimal prices for products and services.
Applications in Medicine and Biology
Mathematical models also play a crucial role in understanding biological processes and medical applications. For example:
- Population Growth: Biologists use differential equations to model the growth of populations, helping predict trends in species behavior and environmental impact.
- Medical Imaging: Advanced imaging techniques like MRI and CT scans rely on mathematical algorithms to reconstruct images of the body, helping doctors diagnose and treat diseases more effectively.
- Pharmacokinetics: In medicine, calculus is used to model the absorption, distribution, metabolism, and excretion of drugs, aiding in the development of effective treatment plans.
Study Resources for AP Calculus BC
Preparing for a challenging exam requires the right set of tools and study materials. Whether you are self-studying or looking to supplement your classroom learning, having access to high-quality resources is essential for mastering key concepts. In this section, we will explore some of the most effective resources that can aid in your preparation, ranging from textbooks to online tools and practice tests.
Textbooks and Study Guides
A strong foundation starts with the right textbook. Textbooks offer detailed explanations, examples, and practice problems that help reinforce important ideas. Some recommended study guides include:
- Advanced Placement Calculus AB/BC: This comprehensive guide covers all the necessary topics with practice problems and solutions.
- AP Calculus BC For Dummies: A user-friendly guide that explains complex concepts in an easy-to-understand manner, perfect for both beginners and those looking to review.
- Calculus: Early Transcendentals by James Stewart: A widely-used textbook that provides in-depth coverage of essential topics with clear explanations and a variety of exercises.
Online Tools and Platforms
The internet is filled with resources that offer interactive ways to study and practice problems. Some online platforms you can use include:
- Khan Academy: This free online resource provides instructional videos and practice exercises on a wide range of topics, including all key areas of the exam.
- College Board’s Official AP Calculus BC Practice: College Board, the organization that administers AP exams, offers free practice tests and sample questions that mirror the exam format.
- Brilliant.org: An interactive platform that offers problem-solving-based learning in mathematics, including courses designed for advanced students.
Practice Tests and Flashcards
Practicing with real or simulated exam questions is one of the best ways to prepare for the test. Here are some additional resources to help you practice:
- AP Classroom: This official resource provides access to past exam questions, practice sets, and personalized feedback to guide your preparation.
- Quizlet: An online flashcard tool where you can find or create flashcards for specific concepts, formulas, and problem-solving techniques.
- AP Exam Prep Books: Books such as the “Barron’s AP Calculus BC” and “Princeton Review’s AP Calculus BC” offer practice tests and solutions with detailed explanations.
By utilizing these resources, you can reinforce your understanding, improve your problem-solving skills, and build the confidence you need to perform well on your exam.
How to Manage Time During the Exam
Efficient time management is crucial when taking a challenging exam. With a limited amount of time and a variety of questions to answer, it’s essential to stay focused and organized to maximize your performance. By developing a strategy for managing your time, you can ensure that you tackle each section effectively without feeling rushed or overwhelmed. In this section, we will discuss practical tips for making the most of your time during the test.
Plan Ahead Before Starting
Before diving into the questions, take a few moments to strategize your approach. This will help you allocate time wisely across different sections. Here are some steps to take:
- Skim the exam: Quickly look over the entire test to get a sense of the question types and their difficulty. This will help you decide how to divide your time.
- Prioritize easy questions: Start with the questions you feel most confident about. Answering them quickly will build momentum and boost your confidence.
- Set time limits: For each section or set of questions, assign a specific time limit. Try to stick to it as closely as possible to avoid spending too much time on one question.
During the Exam: Stay on Track
Once you begin answering questions, it’s important to maintain your focus and avoid getting bogged down by difficult problems. Here are a few tips for staying on track:
- Don’t linger on tough questions: If you encounter a difficult question, don’t waste too much time on it. Mark it and move on to the next one. You can always come back to it later if you have time.
- Keep an eye on the clock: Periodically check the time to ensure you’re staying on schedule. This will help you adjust your pace if needed.
- Review key formulas: Before starting, make sure you have the essential formulas and concepts fresh in your mind. This will reduce time spent searching for information during the test.
How to Handle Time Pressure
It’s common to feel a sense of urgency as time runs out. However, it’s important to stay calm and focus on managing your remaining time effectively:
- Use the last few minutes wisely: In the final minutes, quickly review your answers, especially the ones you were unsure about. Make sure you didn’t miss any questions.
- Check for errors: Double-check calculations or steps that might have been rushed, but don’t spend too much time making small adjustments unless you’re sure they will make a difference.
- Stay positive: Stress can cloud your thinking and slow you down. Take deep breaths and stay focused on the task at hand.
By planning ahead, pacing yourself, and staying focused during the exam, you can improve your time management skills and increase your chances of achieving a high score.
Improving Problem-Solving Speed in Calculus
Efficient problem-solving is a crucial skill when facing time-sensitive exams. The ability to solve complex questions quickly without sacrificing accuracy is essential for maximizing your performance. In this section, we will explore strategies to improve your problem-solving speed, focusing on techniques that allow you to approach challenges with confidence and efficiency.
Familiarity with Key Concepts
One of the most effective ways to solve problems faster is to be thoroughly familiar with the core concepts and methods that underpin the material. When you have a deep understanding of the foundational ideas, you can quickly identify the most appropriate techniques for tackling a given problem. Here are some ways to strengthen your grasp on key principles:
- Practice regularly: Regular practice will help solidify your understanding and make solving problems second nature. The more you practice, the faster you’ll become at recognizing patterns and applying the right methods.
- Master common techniques: Focus on mastering common problem-solving techniques like differentiation, integration, and optimization. Knowing these methods inside and out will allow you to solve problems quickly and without hesitation.
- Use mental shortcuts: As you become more comfortable with the material, you’ll notice opportunities for mental shortcuts that can save valuable time, such as simplifying expressions or recognizing certain forms at a glance.
Improving Speed Through Practice Tests
Simulating real exam conditions through practice tests is an excellent way to improve your speed. By replicating the time constraints of the exam, you’ll get used to solving problems within a limited timeframe, which will help reduce stress and increase your efficiency. Consider these strategies for maximizing your practice test sessions:
- Timed practice: Set a timer for each practice session to simulate exam conditions. This will help you gauge how long you take on each question and identify areas where you can improve your pace.
- Review after practice: After completing a practice test, take the time to carefully review your mistakes. Understanding why you made errors will help you avoid repeating them and improve your speed over time.
- Focus on problem areas: If certain types of questions consistently take longer to solve, focus your practice on these areas. By targeting your weak spots, you can significantly improve your speed for those types of problems.
By combining a strong understanding of the material with regular practice and strategic problem-solving, you can significantly increase your problem-solving speed, making you more confident and effective during exams.