
Preparing for a significant mathematics assessment requires focused effort and a well-structured approach. Understanding the core principles, sharpening problem-solving techniques, and reviewing essential concepts are all key steps in achieving top results. Whether you’re revisiting fundamental algebraic methods or diving into more complex theories, the right preparation can make all the difference.
Effective preparation involves identifying areas where you may need additional practice while reinforcing your strengths. Working through a range of practice questions and applying various strategies will help you tackle different types of challenges that may appear in the test. Taking the time to thoroughly review each topic will ensure you feel confident and capable when it’s time to apply your knowledge.
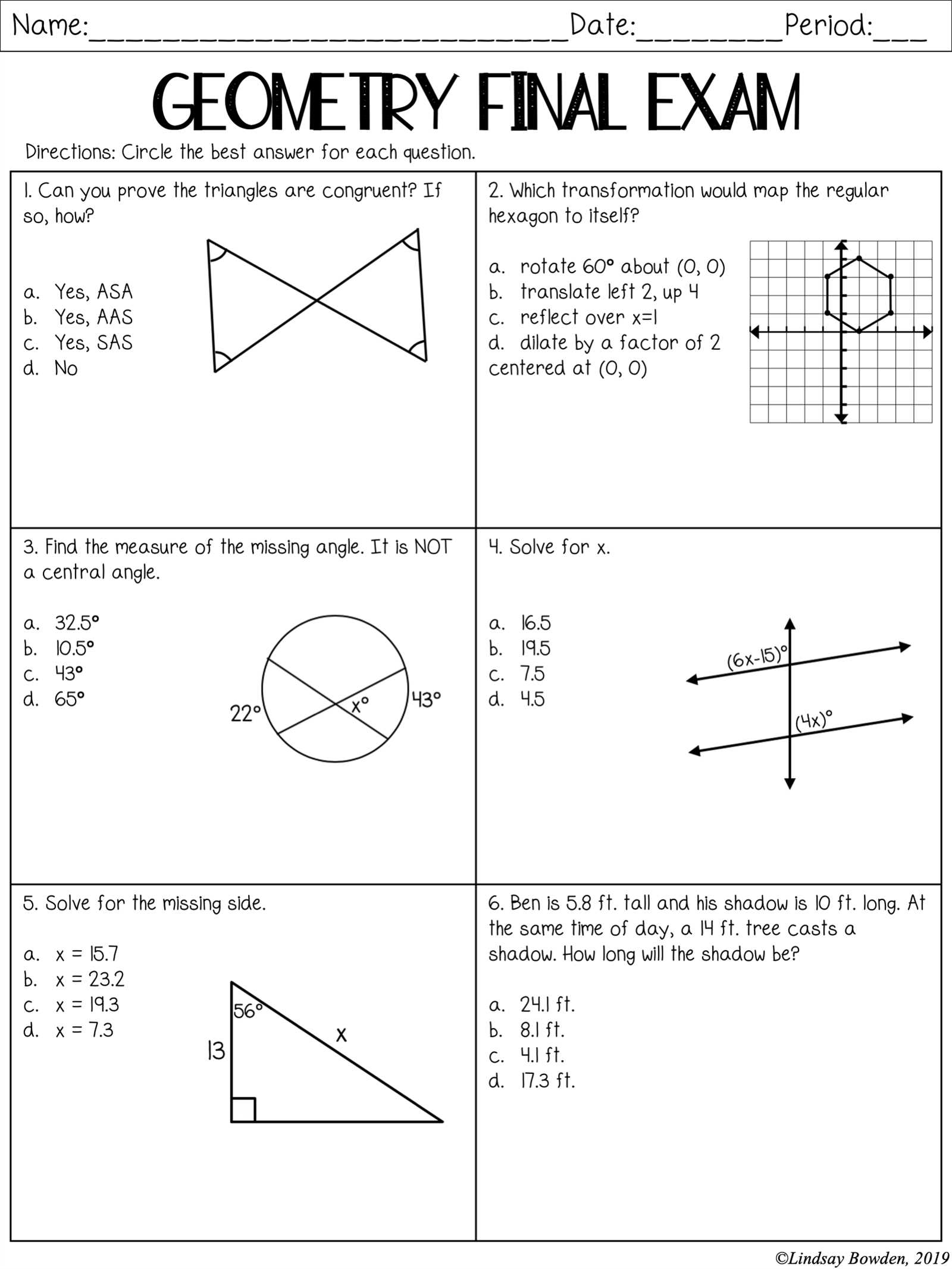
Math 3 Review and Preparation Tips

Approaching a comprehensive assessment requires a strategic and organized approach. To perform well, it’s essential to focus on key topics, refine problem-solving methods, and strengthen areas where you may feel less confident. Reviewing concepts in a structured manner will not only help you remember important details but also enable you to apply your knowledge effectively under pressure.
Key Concepts to Focus On
It’s crucial to identify the central themes of the course that are likely to appear in the test. Start by revisiting algebraic techniques, such as solving equations and manipulating expressions. Additionally, be sure to review geometric principles and trigonometric functions, which often play a significant role in many assessments.
Effective Problem-Solving Strategies
When practicing, try to vary the difficulty level of the questions to ensure you are prepared for any challenge. Work through problems step by step, breaking them down into smaller tasks. This approach will help you avoid feeling overwhelmed and improve your ability to solve questions quickly and accurately.
Understanding Key Math 3 Concepts
Mastering the fundamental principles of advanced mathematics is essential for success. A solid grasp of core topics will enable you to tackle a wide range of problems with confidence. Focus on the underlying concepts rather than just memorizing formulas, as understanding how and why things work will help you apply knowledge effectively in different situations.
Core areas such as algebraic manipulation, geometric reasoning, and functions form the foundation of this subject. It is important to spend time comprehending how equations are derived, how shapes and angles relate, and how different functions behave. This deeper understanding allows you to solve problems more efficiently and prepares you for more complex challenges.
How to Organize Your Study Schedule
Effective preparation starts with a well-structured plan. Breaking down your review time into manageable sessions allows you to focus on specific topics without feeling overwhelmed. By allocating time for each subject, you ensure comprehensive coverage and can track your progress more easily.
Begin by setting clear goals for each study session. Identify the most challenging areas and allocate more time to those topics. Incorporate regular breaks to prevent burnout, and aim to review material consistently rather than cramming all at once. A balanced schedule will help reinforce learning and improve retention over time.
Top Study Resources for Math 3
Finding the right tools can significantly enhance your learning experience. There are many resources available that provide explanations, practice problems, and interactive lessons to help you master key topics. Choosing the best resources tailored to your needs will ensure a more effective preparation process.
Online Platforms for Interactive Learning
Online platforms offer a wide variety of tutorials and exercises that cater to different learning styles. Websites like Khan Academy and Coursera provide free courses that explain complex concepts with clear examples. These resources also offer quizzes and interactive activities to test your understanding and track progress.
Textbooks and Practice Workbooks
While digital resources are valuable, traditional textbooks and workbooks remain essential. They offer detailed explanations of theories and provide a variety of practice questions. Look for books that include step-by-step solutions and a wide range of examples, so you can understand the methodology behind each problem-solving approach. Practice consistently using these materials to reinforce concepts.
Important Formulas to Remember

Mastering essential equations is a key part of achieving success. These formulas form the foundation of many problem-solving techniques and are crucial for quick calculations during an assessment. Familiarizing yourself with these key relationships will ensure you can apply them efficiently in various scenarios.
Below is a table of some of the most important formulas to remember:
| Topic | Formula | Description |
|---|---|---|
| Quadratic Equation | x = (-b ± √(b² – 4ac)) / 2a | Used to solve quadratic equations in the form ax² + bx + c = 0. |
| Pythagorean Theorem | a² + b² = c² | Relates the lengths of the sides of a right triangle. |
| Area of a Circle | A = πr² | Formula to calculate the area of a circle, where r is the radius. |
| Slope of a Line | m = (y₂ – y₁) / (x₂ – x₁) | Formula for calculating the slope between two points (x₁, y₁) and (x₂, y₂). |
| Circumference of a Circle | C = 2πr | Formula to calculate the distance around a circle. |
Reviewing Algebra for the Final Exam
Algebra is a cornerstone of advanced mathematical problem-solving. A strong understanding of algebraic principles will serve as the foundation for tackling more complex concepts. Focusing on key topics such as equations, inequalities, and polynomial functions will prepare you to solve a variety of problems efficiently and accurately.
Solving Equations and Inequalities
Start by revisiting the process of solving linear and quadratic equations. Ensure you are comfortable with both methods of solving, whether by factoring, completing the square, or using the quadratic formula. Similarly, practice solving inequalities and understanding the rules for working with positive and negative values. These skills are fundamental for answering a wide range of questions on the assessment.
Working with Polynomials
Polynomials appear in many areas of mathematics, so mastering their manipulation is crucial. Review how to add, subtract, multiply, and divide polynomials. Be sure to practice factoring higher-degree polynomials and understanding their graphs. Familiarity with these processes will help you recognize patterns and quickly identify solutions when working with complex expressions.
Mastering Geometry for Math 3
Geometry plays a crucial role in many mathematical challenges. A deep understanding of geometric concepts will enable you to visualize and solve problems involving shapes, angles, and spatial relationships. Focusing on key topics such as proofs, properties of triangles, and circles will ensure you are prepared for any geometric problem.
Understanding Geometric Proofs

Geometric proofs require logical reasoning and a clear understanding of theorems. Review key properties and postulates, such as the Pythagorean theorem, congruence, and similarity. Practice writing formal proofs step by step, ensuring each conclusion follows logically from the previous one. This process will sharpen your problem-solving skills and prepare you for more complex geometric arguments.
Properties of Triangles and Circles
Triangles and circles are foundational shapes in geometry. Familiarize yourself with the various types of triangles–equilateral, isosceles, and scalene–and their properties. Similarly, understanding the key properties of circles, such as radius, diameter, and circumference, is essential. Practice applying these concepts to real-world problems to solidify your understanding and increase your confidence.
Tips for Solving Word Problems

Word problems can often seem daunting, but with the right approach, they become much easier to tackle. The key is breaking down the problem into smaller, manageable parts and identifying what the question is really asking. Focusing on the information provided and translating it into mathematical expressions will guide you toward the solution.
Start by identifying the variables–what quantities are you being asked to solve for? Underline important numbers and keywords, then translate them into mathematical symbols or equations. Write out the problem clearly and try to visualize it if possible. Diagrams or drawings can help simplify complex scenarios and make abstract concepts more concrete.
Next, set up your equation or system of equations and solve step by step. Pay close attention to units, as converting them may be necessary. Always double-check your work once you find a solution, ensuring that your final answer makes sense within the context of the problem.
Practice Problems for Effective Review
To truly solidify your understanding, practicing a variety of problems is essential. The more problems you work through, the more familiar you become with the different types of questions and solution strategies. Practice allows you to apply concepts in different contexts, reinforcing your problem-solving skills and boosting your confidence.
Start by tackling problems that cover all the key topics. Begin with simpler questions to build your confidence and gradually increase the difficulty level as you improve. Don’t just memorize the steps–focus on understanding the reasoning behind each solution. Regularly revisit problems you’ve already solved to ensure retention and reinforce your learning.
Time Management During the Exam

Effective time management is critical when facing a timed assessment. Prioritizing tasks and pacing yourself ensures that you can address every question with the attention it deserves, without feeling rushed. A strategic approach to allocating time allows you to stay calm, focused, and confident throughout the entire process.
Start by quickly scanning through the questions at the beginning. Identify the ones that seem easiest and tackle them first, leaving more challenging problems for later. Keep track of time and set mini-deadlines for each section. If you get stuck on a question, move on and return to it later–this helps maintain your momentum and prevents you from spending too much time on any single problem.
How to Handle Test Anxiety
Feeling anxious before or during an assessment is a common experience. While some level of stress can be motivating, excessive worry can negatively affect performance. Developing strategies to manage anxiety allows you to stay focused and calm, ensuring that you can perform at your best even under pressure.
Preparation Techniques

Proper preparation is one of the best ways to reduce anxiety. The more confident you are in your material, the less you’ll stress about the unknown. Use these techniques to get ready:
- Review key concepts consistently rather than cramming at the last minute.
- Practice with past problems to familiarize yourself with the format and difficulty level.
- Simulate test conditions during practice to build comfort with the process.
Relaxation Strategies
In addition to preparation, managing your emotional state is essential. Try incorporating these relaxation methods before and during the assessment:
- Deep breathing: Take slow, deep breaths to help calm your nerves.
- Positive self-talk: Replace negative thoughts with affirmations of confidence.
- Mindfulness: Stay present and avoid overthinking about the outcome.
Common Mistakes to Avoid in Math 3
When working through mathematical problems, it’s easy to make small errors that can have a big impact on your final answer. Recognizing and avoiding these common mistakes will help you improve accuracy and efficiency. Being mindful of these pitfalls ensures that you can confidently approach each question and minimize the chance of errors.
One of the most frequent mistakes is not carefully reading the problem. Misinterpreting what’s being asked or overlooking key details can lead to incorrect solutions. Another common error is rushing through calculations. Taking the time to check each step reduces the likelihood of simple arithmetic mistakes.
Additionally, neglecting to review your work at the end can also be detrimental. Even if you’re sure of your answer, a final check for mistakes can reveal overlooked errors. It’s important to stay focused and avoid jumping to conclusions without verifying your calculations.
Strategies for Multiple Choice Questions
Multiple choice questions can appear straightforward, but they often require careful thought and strategy to answer correctly. Developing a methodical approach to these types of questions helps increase accuracy and confidence. By focusing on the structure of the options and applying certain techniques, you can significantly improve your performance.
Effective Approaches to Answering
Here are several strategies to help you tackle multiple choice questions efficiently:
- Read the question thoroughly before looking at the answer choices to avoid getting distracted by tempting but incorrect options.
- Eliminate obvious wrong answers to increase your chances of selecting the correct one. This simplifies your choices and boosts your odds.
- Look for key terms in the question that match the wording in one or more of the options. Often, correct answers contain these clues.
- Consider all options even if the first choice seems correct. Sometimes the right answer is hidden among seemingly similar options.
Time Management and Final Check
When answering multiple choice questions, managing your time is just as important as choosing the right answer. Follow these tips to improve your efficiency:
- Don’t spend too much time on any one question. If you’re unsure, move on and return to it later.
- Check your answers if time allows. Sometimes, a second look can help you catch a small mistake or a misinterpreted question.
Improving Problem-Solving Speed
Speed is an essential factor when it comes to solving complex problems, especially under time constraints. With consistent practice and effective techniques, you can improve your ability to work through questions quickly without sacrificing accuracy. Developing a faster problem-solving approach involves sharpening your skills, recognizing patterns, and efficiently applying the right methods.
Key Techniques for Faster Solutions

To enhance your problem-solving speed, consider these approaches:
- Practice regularly with timed exercises. The more you practice, the quicker you’ll recognize familiar patterns and shortcuts.
- Master foundational concepts so you don’t waste time re-learning basics during a problem-solving session.
- Work on mental math to reduce reliance on calculators and improve your efficiency with simple calculations.
- Focus on strategies that allow you to approach problems systematically, such as breaking down complex problems into smaller, manageable steps.
Time-Saving Tips During the Process
While solving problems, consider these additional strategies to increase speed:
- Skip overly difficult problems and return to them later if time is limited. Focus on questions that you can solve quickly first.
- Use estimation when appropriate. Estimating the answer can save time on problems that do not require precise solutions.
- Avoid second-guessing your initial answers. Trust your instincts and move on to the next problem to avoid wasting time.
Using Graphing Calculators Effectively
Graphing calculators are powerful tools that can simplify complex calculations and provide visual insights into mathematical functions. Mastering their use can save valuable time and help you better understand the relationships between equations. By becoming familiar with their features, you can solve problems faster and with greater accuracy.
Essential Features to Focus On
To make the most of your graphing calculator, focus on learning these key functions:
- Graphing functions: Understanding how to input and adjust equations for visual representation is crucial. This helps in identifying trends and behavior of functions.
- Using tables: The table feature allows you to quickly compute values for different inputs, helping you spot patterns in your data.
- Zoom and window settings: Adjusting these settings lets you control the view of your graph, making it easier to focus on the most relevant parts of a function.
- Solving equations: Many calculators offer tools to solve equations, making it easier to find roots and intercepts without manually calculating.
Tips for Efficient Use During Problem Solving
Maximizing the efficiency of your calculator can help you solve problems quickly and accurately:
- Practice with different functions: Familiarize yourself with functions like derivatives, integrals, and solving systems of equations, which can save time during complex calculations.
- Set clear input settings: Make sure to adjust the mode (e.g., radians or degrees) and settings based on the problem to avoid errors.
- Check for mistakes: Double-check inputs, especially when working with multi-step problems, as small mistakes can lead to incorrect results.
- Use shortcuts: Learn the specific key combinations and shortcuts for faster input and navigation during problem-solving sessions.
What to Do the Night Before the Exam
The day before an important assessment is crucial for ensuring you’re in the right state of mind and ready for success. It’s not just about cramming information; it’s about preparing both mentally and physically to perform your best. The night before is the perfect time to consolidate your knowledge and relax, allowing your brain to process everything you’ve learned.
First and foremost, avoid overwhelming yourself with new information. Focus on reviewing key concepts and strategies, but don’t stress over trying to learn something completely new. Trust that you’ve put in the work leading up to this point. Make sure to gather all the materials you’ll need for the next day, such as pens, calculators, and any necessary documents, so you don’t feel rushed or anxious in the morning.
Equally important is ensuring a good night’s sleep. Rest is essential for cognitive function, memory recall, and staying calm under pressure. Make sure to set an alarm and have everything prepared the night before, so you can wake up feeling refreshed and confident.
Post-Exam Reflection and Review

After completing an important assessment, it’s valuable to take time to reflect on your performance and identify areas for growth. This process helps reinforce what you’ve learned and can provide insights into how you can improve for future challenges. Rather than focusing on outcomes, use this time to assess the strategies that worked and pinpoint where adjustments could be made.
Begin by reviewing the questions you found most challenging. What was the cause of your difficulty? Was it a misunderstanding of the material, time management issues, or perhaps stress during the process? By pinpointing specific areas of weakness, you can better focus your efforts in the future.
Additionally, it’s helpful to reflect on the overall approach you took. Did you feel confident going in, or were there last-minute doubts? Consider how your preparation and mindset affected your performance. Creating a summary of your strengths and weaknesses after each assessment can be an excellent tool for personal growth.
| Area | Action |
|---|---|
| Time Management | Focus on allocating time more efficiently during future tests. |
| Concepts Struggled With | Spend additional time reviewing challenging topics and practice more questions. |
| Confidence Levels | Improve relaxation techniques to reduce test anxiety and boost confidence. |
Overall, the post-assessment reflection provides a valuable opportunity to grow both academically and personally, preparing you for future challenges with a clearer understanding of your strengths and areas for improvement.
Preparing for Future Math Courses
Looking ahead to more advanced topics in the field, it’s important to build a strong foundation. As you move forward in your academic journey, having a thorough understanding of key concepts will help you succeed in more complex areas. Planning ahead, reviewing what you’ve learned, and identifying gaps in knowledge can set you up for success in upcoming challenges.
One of the most effective ways to prepare is by revisiting core principles. Make sure that you have a solid grasp of basic concepts before tackling higher-level material. Whether it’s revisiting fundamental operations, functions, or graphing techniques, strengthening your foundation will make future coursework easier to grasp.
Additionally, start exploring new topics that will be covered in the next level of your studies. Familiarizing yourself with the content beforehand allows for a smoother transition when the time comes. It can also spark curiosity and enthusiasm, helping you remain motivated to continue progressing.
Consider forming study groups or seeking additional resources, such as online courses or tutoring, to enhance your understanding. Collaborative learning and external support can provide different perspectives and insights that might help clarify difficult concepts.