
As the semester draws to a close, students often face the challenge of preparing for their comprehensive review. This stage can be overwhelming, but with the right approach, it becomes manageable. Understanding the core concepts and honing your problem-solving skills are essential for achieving success. By focusing on key areas of the subject, you can approach the test with confidence and clarity.
Effective preparation involves more than just memorizing facts; it requires a deep understanding of the material. Whether you’re revisiting equations, analyzing graphs, or practicing real-world applications, each topic contributes to the overall mastery of the subject. Prioritizing areas that you find most challenging can make the difference between struggling and excelling.
Strategic study sessions and consistent practice are crucial components of a successful review. By utilizing resources such as textbooks, online tools, and study groups, you can reinforce your knowledge and increase your chances of success. With dedication and the right mindset, you will be well-prepared for the assessment ahead.
End-of-Term Review Solutions
The key to excelling in a comprehensive assessment lies in mastering the core concepts and applying them effectively under time pressure. This section will guide you through the necessary steps to review essential topics and provide clarity on the most frequently tested concepts. By working through practice questions and analyzing solutions, you will strengthen your problem-solving abilities and build confidence for the upcoming test.
Key Areas to Focus On
Focus on understanding the foundational principles that underpin the subject matter. Revisit equations, functions, and theorems, ensuring that you can both recall and apply them in various contexts. Pay special attention to areas that you find difficult, as these will likely appear in different forms during the assessment. Practicing a variety of questions from each section will help you refine your approach and sharpen your skills.
Effective Strategies for Success
To maximize your chances of success, adopt a strategic approach to your preparation. Break down your study sessions into manageable chunks, and dedicate specific times to review different topics. Consistent practice with timed mock problems will help simulate the actual testing environment and improve your time management. By reinforcing your understanding and improving your problem-solving speed, you will be better equipped to tackle even the most challenging questions.
Key Concepts for the Final Assessment
In order to perform well on a comprehensive evaluation, it is essential to focus on the most important concepts that form the foundation of the subject. This section will highlight the critical topics that you need to master before the test. Understanding these core areas will allow you to approach questions with confidence and precision.
Core Topics to Review
When preparing for the evaluation, ensure that you have a solid grasp of the following key concepts:
- Functions and Graphs: Be familiar with interpreting and manipulating different types of functions, including linear, quadratic, and exponential functions.
- Systems of Equations: Understand methods for solving systems of equations, including substitution, elimination, and graphing.
- Probability and Statistics: Know how to calculate and interpret probabilities, and understand statistical concepts like mean, median, and standard deviation.
- Trigonometric Functions: Study the properties of trigonometric functions and their applications in solving real-world problems.
- Polynomials and Rational Expressions: Practice simplifying, factoring, and performing operations with polynomials and rational expressions.
Problem-Solving Strategies
Mastering the following strategies will help you navigate the problems with greater ease:
- Identify Key Information: Carefully read each question to identify what is being asked and determine which concepts apply.
- Work Step-by-Step: Avoid rushing. Break down problems into manageable steps and solve them methodically.
- Check Your Work: After solving each problem, review your steps to ensure accuracy and identify any potential mistakes.
Important Topics to Focus On
To ensure you perform at your best, it is crucial to prioritize the topics that carry the most weight and are often featured in assessments. Focusing on these key areas will give you a solid foundation and help you tackle a wide variety of problems. Below, we have outlined the most important subjects you should dedicate extra time to in order to maximize your preparation.
Core Areas to Review
Concentrating on these subjects will provide you with the tools needed to solve most problems that arise during the evaluation:
| Topic | Why It’s Important | Key Concepts |
|---|---|---|
| Functions | Understanding how to manipulate and graph various types of functions is crucial. | Linear, quadratic, exponential |
| Systems of Equations | Systems often appear in multiple forms and require different solving methods. | Substitution, elimination, graphing |
| Trigonometry | Trigonometric identities and solving problems using angles are frequently tested. | Sine, cosine, tangent, unit circle |
| Polynomials | Being able to factor and simplify polynomial expressions is fundamental for problem solving. | Factoring, long division, synthetic division |
| Statistics | Statistical concepts help interpret data and solve probability-related questions. | Mean, median, variance, standard deviation |
Additional Areas to Strengthen
While the above topics are essential, make sure to also strengthen your understanding of:
- Rational expressions and equations
- Graphing techniques for different functions
- Word problems and applying concepts to real-life situations
How to Approach Problem Solving
Effective problem solving requires a structured approach that helps break down complex tasks into manageable steps. By following a consistent method, you can increase your efficiency and accuracy, ensuring you tackle every challenge systematically. Below are some essential strategies that will assist you in approaching each problem with confidence and clarity.
Problem Solving Strategy
The following steps will guide you through any challenging question you encounter:
| Step | Description |
|---|---|
| 1. Understand the Problem | Carefully read the problem to identify key information and what is being asked. |
| 2. Identify Relevant Concepts | Determine which mathematical principles or methods apply to the given problem. |
| 3. Develop a Plan | Outline a strategy for solving the problem, considering different approaches or formulas. |
| 4. Solve the Problem | Work through the problem step by step, following the plan you’ve developed. |
| 5. Review and Verify | Check your solution to ensure it is correct and makes sense in the context of the problem. |
Common Problem-Solving Mistakes

While solving problems, it’s important to be aware of common pitfalls to avoid:
- Rushing through the steps without fully understanding the question.
- Overcomplicating the solution by using unnecessary methods.
- Forgetting to double-check calculations and results.
Common Mistakes to Avoid
Even the most prepared individuals can fall into certain traps during an assessment. Being aware of these common mistakes and taking steps to avoid them can significantly improve your performance. Below are some of the most frequent errors that students make and how to prevent them.
Rushing Through Questions is one of the biggest pitfalls. It’s easy to feel pressed for time, but working too quickly can lead to careless mistakes. Always take the time to read the problem thoroughly before jumping into calculations.
Misinterpreting the Problem can lead to solving the wrong equation or applying the wrong method. Carefully analyze the question to make sure you fully understand what is being asked before proceeding.
Skipping Steps might seem like a time-saver, but it often leads to mistakes. Even if you can perform calculations mentally, writing out each step ensures that you don’t overlook critical details. Clarity in your process is just as important as the final solution.
Not Double-Checking Work is another common error. It’s easy to assume everything is correct, but errors can creep in unnoticed. After completing a problem, always take a moment to review your solution and verify each step.
Overcomplicating Solutions can also cause unnecessary mistakes. Sometimes, the simplest approach is the most effective. Stick to the method that best fits the problem and avoid introducing complexity where it’s not needed.
Understanding the Assessment Format
Familiarizing yourself with the structure of an upcoming evaluation is a crucial step in effective preparation. Knowing what to expect in terms of question types, difficulty level, and time constraints can help you allocate your time efficiently and approach each section with confidence. Below is a breakdown of the typical format and how you can best prepare for each part.
Types of Questions
The assessment is likely to include various question formats. Here are the most common types:
- Multiple Choice: These questions test your ability to recognize the correct answer from a set of options. Pay attention to all choices before selecting your answer.
- Short Answer: You will need to provide a brief response, often requiring the application of specific formulas or principles. Ensure clarity and accuracy in your explanation.
- Problem Solving: These questions typically require you to show your work and apply various methods to arrive at the solution. Make sure to break down each step methodically.
- True/False: Read each statement carefully and justify your answer based on your understanding of the material.
Time Management Tips
Understanding how much time to spend on each section can make a big difference. Consider the following strategies:
- Prioritize Questions: Start with the questions you feel most confident about to build momentum and save time for more difficult ones.
- Set Time Limits: Allocate a specific amount of time for each section or question to avoid spending too much time on one part.
- Review Your Work: If time permits, always go back and check your answers for any errors or omissions.
By understanding the structure and practicing within these parameters, you will be well-prepared to tackle the assessment efficiently and with confidence.
Top Study Resources for Success
To excel in any evaluation, it’s important to utilize a variety of study materials that cater to different learning styles. Whether you prefer hands-on practice, visual aids, or in-depth reading, there are numerous resources available to support your preparation. The following list includes some of the most effective tools to help you succeed.
Essential Study Materials
- Textbooks: The core material of any course, textbooks provide detailed explanations and examples. Be sure to review the chapters related to the key concepts and practice exercises.
- Online Tutorials: Platforms like Khan Academy, Coursera, and YouTube offer free tutorials on a variety of topics. These resources break down complex ideas into digestible lessons and often include problem-solving examples.
- Study Guides: Comprehensive study guides are a great way to review essential topics. Many guides offer summaries, practice questions, and step-by-step solutions.
- Practice Tests: Take advantage of practice assessments available online or through your institution. These simulate real testing conditions and help you identify areas where you may need more focus.
- Flashcards: Digital and physical flashcards are excellent for reinforcing formulas, definitions, and key concepts. Tools like Quizlet allow you to create custom sets and practice on the go.
Interactive and Collaborative Learning
In addition to traditional study materials, engaging with others and practicing actively can greatly enhance your retention and understanding.
- Study Groups: Join or create study groups with classmates. Collaborating with others allows you to explain concepts, ask questions, and gain different perspectives.
- Online Forums and Communities: Websites like Reddit and Stack Exchange offer vibrant communities where you can ask questions, share resources, and discuss topics in detail.
- Educational Apps: Many apps are designed to help reinforce learning. From problem-solving apps to math-specific tools, these resources make learning interactive and fun.
By utilizing these resources effectively, you can create a comprehensive study plan that caters to all aspects of your preparation, ensuring that you are well-prepared for the challenge ahead.
Tips for Efficient Time Management
Effective time management is crucial for success in any task that involves problem-solving and critical thinking. Organizing your time wisely not only helps you complete tasks efficiently but also reduces stress and boosts confidence. Below are several strategies to help you manage your study time more effectively.
Key Time Management Strategies
- Set Clear Goals: Break down your study material into smaller, manageable tasks. Focus on specific objectives for each study session.
- Use a Planner: Organize your daily schedule to ensure you allocate time for each subject or topic. Mark important dates and deadlines to avoid last-minute stress.
- Prioritize Tasks: Identify the most important or challenging areas and tackle those first. Completing difficult tasks early on will give you a sense of accomplishment and reduce pressure.
- Set Time Limits: Allocate specific amounts of time for each task to avoid spending too much time on any one area. This helps maintain focus and prevents procrastination.
Maximizing Efficiency
Adopting these additional practices can further enhance your productivity:
- Use the Pomodoro Technique: Work in focused intervals of 25 minutes, followed by a 5-minute break. After four sessions, take a longer break. This method helps maintain concentration and prevents burnout.
- Avoid Multitasking: Focus on one task at a time to ensure high-quality work. Trying to juggle multiple tasks often leads to mistakes and decreased efficiency.
- Review Regularly: Allocate time at the end of each study session to go over what you’ve learned. This reinforces concepts and helps identify areas needing further attention.
By following these time management techniques, you can maximize your productivity, reduce stress, and approach your tasks with a clear and organized mindset.
Practice Problems and Solutions
Working through problems and reviewing solutions is one of the most effective ways to prepare for any assessment. By practicing different types of questions, you not only reinforce your understanding of concepts but also improve your problem-solving skills. This section provides a set of practice problems followed by detailed solutions to help you assess your progress and deepen your knowledge.
Sample Problems
Below are some sample problems that you can use to test your skills:
- Problem 1: Solve the equation for x: 3x + 7 = 16
- Problem 2: Simplify the expression: (2x + 3)(x – 5)
- Problem 3: Find the area of a triangle with a base of 10 units and height of 8 units.
- Problem 4: Solve the system of equations:
- 2x + y = 5
- x – y = 2
Step-by-Step Solutions
Here are the solutions to the practice problems:
- Solution 1: To solve 3x + 7 = 16, subtract 7 from both sides to get 3x = 9. Then divide both sides by 3 to find x = 3.
- Solution 2: To simplify (2x + 3)(x – 5), use the distributive property:
- 2x(x) = 2x²
- 2x(-5) = -10x
- 3(x) = 3x
- 3(-5) = -15
Combine like terms: 2x² – 10x + 3x – 15 = 2x² – 7x – 15.
- Solution 3: The area of a triangle is given by the formula: Area = 1/2 × base × height. Substituting the values: Area = 1/2 × 10 × 8 = 40 square units.
- Solution 4: To solve the system of equations:
- From x – y = 2, solve for x: x = y + 2.
- Substitute x = y + 2 into 2x + y = 5: 2(y + 2) + y = 5, which simplifies to 2y + 4 + y = 5, or 3y + 4 = 5. Subtract 4 from both sides to get 3y = 1. Divide by 3 to find y = 1/3.
- Substitute y = 1/3 back into x = y + 2: x = 1/3 + 2 = 7/3.
The solution is x = 7/3 and y = 1/3.
By regularly practicing problems like these and reviewing the solutions, you’ll be able to improve your understanding and increase your confidence when facing similar challenges.
Strategies for Answering Word Problems
Word problems can often seem intimidating, but with the right approach, they become much easier to solve. The key is to break the problem down into manageable steps and to carefully analyze the information provided. By using a structured method, you can tackle even the most complex scenarios with confidence.
Here are some effective strategies for approaching word problems:
- Read the Problem Carefully: Begin by reading the problem thoroughly. Make sure you understand what is being asked and identify the key information provided. Sometimes, important details are hidden in the text.
- Identify the Unknowns: Determine what you need to find. Assign variables to the unknown quantities to make the problem easier to solve. Labeling the unknowns will help keep the problem organized.
- Translate Words into Equations: Convert the word problem into mathematical expressions. Look for keywords that signal operations, such as “sum” for addition, “difference” for subtraction, “product” for multiplication, and “quotient” for division.
- Draw a Diagram: If applicable, drawing a picture or diagram can help visualize the problem. This is especially helpful in geometry or problems involving distances, rates, and times.
- Check for Units: Pay close attention to the units used in the problem. Make sure that they are consistent throughout your solution, and convert them if necessary to avoid mistakes.
- Solve and Verify: Once you have translated the problem into a solvable equation, perform the necessary calculations. After finding a solution, go back and verify that your answer makes sense in the context of the problem.
By following these strategies, you can approach word problems systematically and confidently. Practice will further improve your ability to identify key information and find the most efficient way to solve each problem.
Using Calculators Effectively
Calculators are powerful tools that can significantly speed up problem-solving, but they should be used wisely. Simply entering numbers without understanding the underlying concepts can lead to errors or incomplete solutions. To make the most of a calculator, it’s important to use it strategically and understand when and how to apply it in different types of problems.
Here are some tips for using calculators effectively:
- Understand Your Calculator: Familiarize yourself with the functions and features of your calculator. Know how to access advanced operations like fractions, square roots, exponents, and trigonometric functions. Practice using the calculator to ensure you can navigate it quickly during problem-solving.
- Use Parentheses for Clarity: When dealing with complex expressions, use parentheses to group operations and avoid mistakes in order of operations. This ensures that the calculator processes the problem correctly.
- Check for Rounding: Some calculators automatically round decimals. Make sure to adjust the settings or check your answers carefully if precise values are required. Rounding too early in the process can lead to inaccurate results.
- Break Problems Into Steps: If the problem involves multiple steps, break it down into smaller parts. For example, first calculate intermediate results and then combine them to find the final answer. This will help reduce the chance of making calculation errors.
- Use Memory Functions: Many calculators have memory functions that allow you to store intermediate results. Use this feature to hold values that you’ll need later, so you don’t have to re-enter numbers and risk making errors.
- Double-Check Your Results: After calculating, review your answer. Does it make sense in the context of the problem? If possible, estimate the result to see if it is reasonable. This can help you spot any errors or miscalculations.
By using these techniques, you can maximize the effectiveness of your calculator and avoid common pitfalls. With practice, you’ll develop the ability to quickly and accurately solve problems while ensuring the integrity of your calculations.
Reviewing Algebra and Functions
Algebra and functions form the foundation of many mathematical concepts and are essential for solving a wide variety of problems. A strong understanding of these topics will allow you to approach complex equations and real-world scenarios with ease. Whether it’s solving for unknown variables, simplifying expressions, or analyzing relationships between quantities, reviewing these concepts is crucial for success.
To help you refresh and reinforce your knowledge, here are key topics to focus on when reviewing algebra and functions:
Key Algebraic Concepts
- Solving Linear Equations: Being able to solve equations involving variables and constants is fundamental. Practice isolating the variable, working with coefficients, and understanding both one-step and multi-step solutions.
- Factoring Expressions: Factoring is a key skill in algebra. Practice factoring polynomials, especially quadratics, and become comfortable with techniques like the difference of squares and trinomials.
- Working with Exponents: Review the laws of exponents and practice simplifying expressions that involve powers, including negative exponents and fractional exponents.
- Systems of Equations: Understand methods for solving systems of equations, such as substitution and elimination, as well as using matrices for more complex systems.
Understanding Functions
- Defining Functions: Make sure you understand how functions are defined, the difference between independent and dependent variables, and the concept of domain and range.
- Graphing Functions: Reviewing the graphs of common functions (linear, quadratic, exponential) will help you visualize their behavior. Practice identifying key features such as intercepts, slope, and asymptotes.
- Function Operations: Understand how to add, subtract, multiply, and divide functions, and practice combining them to form new expressions.
- Inverse Functions: Review how to find the inverse of a function and when it is applicable, especially in problems involving one-to-one relationships.
By revisiting these algebraic principles and functional concepts, you’ll be better equipped to tackle more complex topics and excel in problem-solving tasks.
Preparing for Geometry Questions
Geometry questions often involve visualizing and manipulating shapes, understanding spatial relationships, and applying various formulas. These questions can range from basic properties of shapes to more complex problems involving areas, volumes, and angles. A strong grasp of geometric principles is key to approaching these problems efficiently and accurately.
Here are some essential topics to review and strategies to employ when preparing for geometry-related problems:
Key Geometry Concepts
- Properties of Shapes: Review the characteristics of common geometric shapes, such as triangles, quadrilaterals, circles, and polygons. Focus on understanding their properties, like side lengths, angles, and symmetry.
- Area and Perimeter Calculations: Be comfortable with formulas for calculating the area and perimeter of basic shapes, such as rectangles, circles, and triangles, as well as composite shapes.
- Volume and Surface Area: Understand how to calculate the volume and surface area of three-dimensional objects, including prisms, cylinders, cones, and spheres.
- Angles and Their Relationships: Refresh your knowledge of angle types (acute, obtuse, right) and the relationships between angles in parallel lines, intersecting lines, and polygons. Practice applying the angle sum property in triangles and other polygons.
Practical Strategies for Problem Solving
- Draw Diagrams: Whenever possible, sketch the problem. A visual representation can make it much easier to identify relevant properties and apply the right formulas.
- Use Theorems and Postulates: Familiarize yourself with key geometric theorems such as the Pythagorean theorem, properties of similar triangles, and theorems related to circles. These can be powerful tools for solving complex problems.
- Practice Word Problems: Many geometry questions involve applying concepts to real-world situations. Practice interpreting word problems, extracting the necessary information, and setting up equations to solve the problem.
By reviewing these fundamental concepts and practicing problem-solving techniques, you’ll be better prepared to tackle geometry questions effectively and confidently.
Mastering Probability and Statistics
Probability and statistics are essential tools for understanding and analyzing data, making predictions, and solving real-world problems. These topics involve techniques for interpreting random events, calculating likelihoods, and analyzing datasets to identify trends or patterns. Mastering these concepts is crucial for solving a wide range of problems efficiently and accurately.
Below are key areas to focus on and strategies for mastering probability and statistics:
Key Concepts in Probability
- Probability Theory: Understand the fundamental principles of probability, including events, sample spaces, and probability distributions. Familiarize yourself with basic concepts such as independent and dependent events, mutually exclusive events, and conditional probability.
- Counting Techniques: Review methods for calculating the number of possible outcomes in a given situation, such as permutations and combinations, and how they relate to probability calculations.
- Probability Distributions: Study different types of probability distributions, such as binomial and normal distributions, and learn how to use them to model real-world scenarios.
Key Concepts in Statistics
- Descriptive Statistics: Learn how to summarize and describe datasets using measures such as mean, median, mode, range, variance, and standard deviation. Understand how to interpret these measures to gain insights from data.
- Hypothesis Testing: Understand the process of formulating and testing hypotheses using statistical tests. Familiarize yourself with concepts such as null and alternative hypotheses, p-values, and confidence intervals.
- Correlation and Regression: Review techniques for analyzing relationships between variables, including correlation coefficients and linear regression. Learn how to interpret the strength and direction of relationships in data.
By strengthening your understanding of probability and statistics, you’ll be equipped to analyze data, make informed decisions, and approach complex problems with confidence.
Handling Trigonometry Problems
Trigonometry deals with the relationships between the angles and sides of triangles, and it is fundamental to various fields, such as physics, engineering, and architecture. Understanding key concepts like sine, cosine, tangent, and their applications can help solve problems involving triangles, periodic functions, and angular measurements. Mastering this topic requires a combination of theoretical knowledge and practical problem-solving techniques.
Below are important concepts and strategies to help you tackle trigonometry challenges with confidence:
Key Trigonometric Functions
- Sine, Cosine, and Tangent: These are the primary trigonometric ratios used to relate the angles and sides of right-angled triangles. Understand their definitions and how to use them in different contexts.
- Inverse Trigonometric Functions: Learn how to solve for angles using inverse functions like arcsine, arccosine, and arctangent, especially when dealing with known side lengths.
- Unit Circle: The unit circle is crucial for understanding the behavior of trigonometric functions beyond right triangles. Familiarize yourself with key angle values on the unit circle and how to compute sine and cosine for various angles.
Solving Trigonometric Equations
When solving trigonometric equations, it is important to apply various identities and strategies to simplify and solve for the unknown. The following table outlines some key trigonometric identities that are essential in simplifying expressions and solving equations:
| Identity | Formula | Usage |
|---|---|---|
| Pythagorean Identity | sin²(θ) + cos²(θ) = 1 | Use this identity to simplify expressions involving sine and cosine. |
| Sum and Difference Identities | sin(A ± B) = sin(A)cos(B) ± cos(A)sin(B) | Use to express trigonometric functions of sums or differences of angles. |
| Double Angle Identities | sin(2θ) = 2sin(θ)cos(θ) | Helpful for solving equations that involve multiples of angles. |
| Half Angle Identities | sin(θ/2) = ±√[(1 – cos(θ))/2] | Use when solving for angles that involve half of a known angle. |
By practicing these techniques and familiarizing yourself with the key identities and formulas, you can confidently handle various trigonometry problems, whether they involve right triangles, general angles, or periodic functions.
Last-Minute Study Tips
As the day approaches to demonstrate your understanding, it’s essential to maximize the time remaining for efficient preparation. Focusing on key topics and adopting strategic methods can help you reinforce what you’ve already learned and tackle any areas of weakness. Even with limited time, these strategies can increase your confidence and improve your performance.
Here are some practical last-minute tips to help you prepare effectively:
Focus on High-Yield Topics
- Prioritize Key Concepts: Concentrate on the most critical topics that are likely to appear, based on past experience or available study materials. Mastering these areas can give you a solid foundation for tackling any related questions.
- Review Practice Problems: Work through as many sample questions as possible, especially those that cover a variety of concepts. This will help you familiarize yourself with question formats and test your ability to apply the material.
- Use Summary Sheets: Quickly go through summary notes or formula sheets to refresh your memory on essential equations, definitions, and concepts.
Effective Time Management
With limited time remaining, it’s crucial to allocate your study hours wisely. The table below provides an approach to structuring your remaining time efficiently:
| Time Block | Focus Area | Activity |
|---|---|---|
| 1 Hour | High-Priority Topics | Review key concepts, formulas, and solve practice problems. |
| 30 Minutes | Weak Areas | Identify and focus on concepts you feel least confident about. |
| 15 Minutes | Quick Review | Go over your summary sheets and main points one last time. |
| 5 Minutes | Relaxation | Take a few minutes to relax and clear your mind before the task begins. |
By following these tips and staying calm, you can maximize the remaining time and enter your session feeling prepared and confident.
How to Stay Calm During the Exam
When it’s time to demonstrate your knowledge, it’s easy to feel overwhelmed or anxious. However, staying composed is crucial for optimal performance. Maintaining a clear and focused mindset allows you to approach each question with confidence and clarity, rather than feeling rushed or stressed. Here are some strategies to help keep your nerves in check during the assessment:
Practice Deep Breathing
Before and during the task, take slow, deep breaths. This simple technique helps reduce anxiety, calms the nervous system, and clears your mind. Focus on your breathing for a few moments to center yourself. If you start feeling anxious, pause and breathe deeply to regain composure.
Break the Task Into Manageable Steps
When faced with a large or complicated problem, break it down into smaller, more manageable parts. Tackling each section individually can make the entire process feel less daunting and will help you focus on one thing at a time. This method prevents you from feeling overwhelmed and allows you to track your progress step by step.
Stay Positive and Focused
Maintain a positive attitude throughout the task. Negative thoughts such as “I’m not prepared” or “This is too hard” can increase stress. Instead, remind yourself that you have prepared and that you are capable of handling the challenge. Focus on the present moment, one question at a time, and trust your preparation.
Manage Your Time Effectively
Time management plays a significant role in reducing anxiety. Keep track of the time, but avoid obsessing over the clock. Prioritize questions you feel most confident about, and allocate time to revisit tougher ones if necessary. A well-structured approach will help you feel more in control and less rushed.
By practicing these techniques, you can approach the task with a clear mind and perform to the best of your abilities. Staying calm is not only about managing stress but also about creating an environment that allows you to think clearly and effectively tackle each challenge.
What to Do After the Exam
After completing an assessment, it’s natural to feel a mix of relief and curiosity about the outcome. However, it’s important to use this time wisely and not dwell too much on the task itself. Instead of overthinking your performance, focus on recovery, reflection, and planning for the future. Here are a few steps to take after you’ve finished an evaluation:
Relax and Unwind
Once the task is over, give yourself permission to relax. Engage in activities that help you unwind, such as taking a walk, reading a book, or spending time with friends. Mental rest is essential for your well-being and will help clear your mind. Taking a break is an important step in the process of recuperation, allowing you to recharge before moving on to your next project or challenge.
Reflect on Your Performance
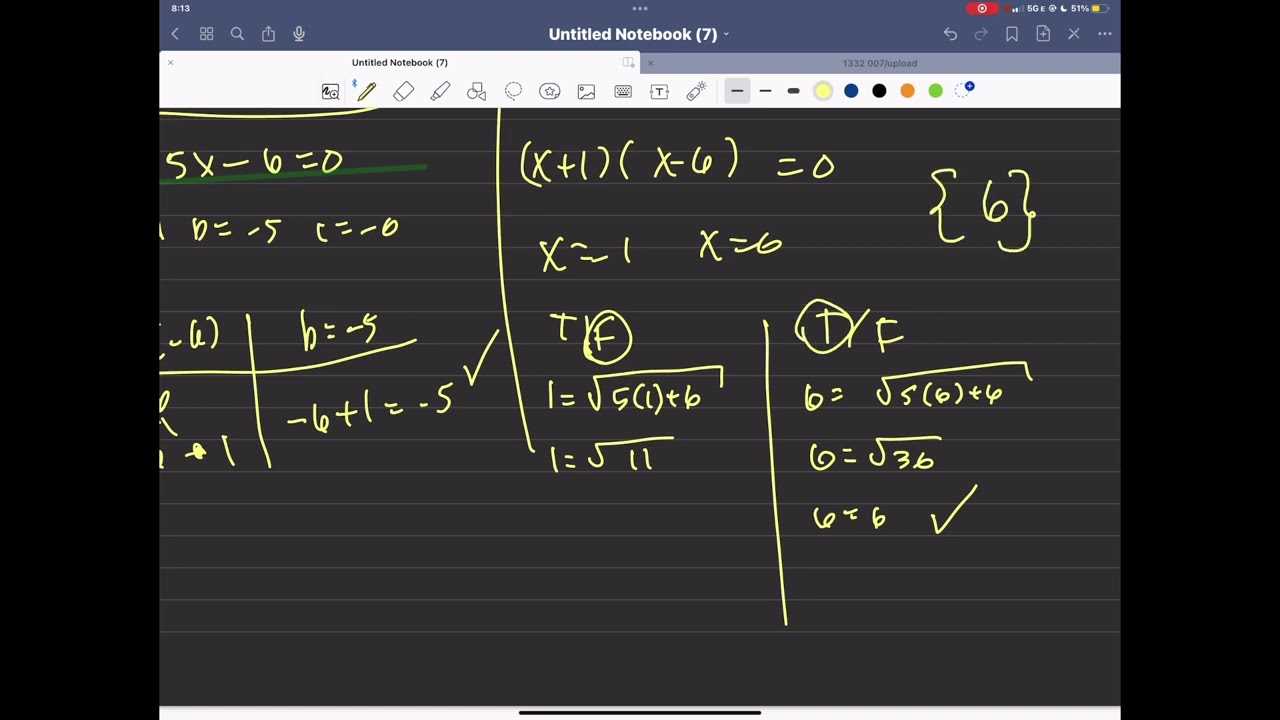
After taking some time to rest, reflect on how the task went. Consider what went well and what areas you found challenging. This reflection will provide valuable insights into your strengths and weaknesses. Use this information to guide your future preparation and improve your skills. The key is not to criticize yourself but to view the experience as an opportunity for growth.
Stay Positive and Be Patient
Waiting for the results can be nerve-wracking, but it’s important to stay positive and patient. Remember that no matter the outcome, you’ve put in the effort, and that’s what matters most. Focus on what you can control–your preparation for future tasks–and maintain a positive attitude as you await feedback.
After the assessment is behind you, use the opportunity for growth and self-care. Stay calm, reflect, and make the most of the time between assessments to continue honing your skills and building your confidence for the next challenge.