
As students progress through their educational journey, understanding core concepts becomes essential for their success. This section is dedicated to guiding learners through key topics encountered in their studies. By breaking down complex problems into manageable steps, students can gain confidence and sharpen their skills.
In this resource, you’ll find comprehensive explanations and detailed solutions aimed at helping students grasp important mathematical principles. With clear, structured approaches, each concept is made more accessible, ensuring that no student is left behind. Whether it’s working through calculations, solving real-world problems, or mastering formulas, this guide offers the tools needed to excel.
Empower your learning experience with practical insights and solutions that promote understanding and long-term retention.
California Go Math 6th Grade Answers

This section is designed to support students in mastering key concepts through clear, step-by-step guidance. Focusing on a range of essential topics, it provides solutions to problems typically encountered in the classroom. By breaking down each concept into easy-to-understand explanations, learners can build a solid foundation for success.
Breaking Down Key Concepts
Understanding complex topics can often feel overwhelming. However, by working through examples and seeing solutions in a structured way, students can simplify even the most challenging questions. This approach not only helps with immediate homework but also strengthens problem-solving skills for future learning.
Practical Application of Problem-Solving Skills
Effective learning goes beyond just solving problems–it involves applying these skills to real-life situations. With the correct tools and practice, students will find that the methods they learn today can be applied to future academic and practical challenges. The goal is to foster a deeper understanding that students can carry forward.
Understanding the Go Math Curriculum
The program is designed to help students develop a strong grasp of essential mathematical principles through an interactive and progressive approach. By organizing content into manageable sections, it allows learners to master each concept before advancing to the next. The curriculum encourages both conceptual understanding and practical application, preparing students for more advanced topics in the future.
Core Topics and Structure
The program is divided into thematic units that cover a wide range of subjects, from basic operations to more complex problem-solving strategies. Each unit is structured to build on previous knowledge, ensuring students have a solid foundation before tackling new material. The approach emphasizes the importance of critical thinking and logical reasoning, which are essential for solving real-world challenges.
Interactive Learning and Support
To keep students engaged, the curriculum incorporates various learning tools such as interactive activities, quizzes, and detailed practice exercises. These resources provide immediate feedback, enabling learners to track their progress and identify areas for improvement. By utilizing this approach, the program helps students not only understand the material but also retain it effectively over time.
Key Concepts in Grade 6 Math

At this level, students encounter several fundamental topics that lay the groundwork for more advanced mathematical study. Understanding these core ideas is crucial for building problem-solving abilities and fostering a deeper appreciation for how mathematics applies to real-world situations. The key concepts are designed to challenge students, helping them to develop logical thinking and analytical skills.
Fractions, Decimals, and Percentages
A major focus in this stage is working with fractions, decimals, and percentages. These concepts are essential for handling everyday situations, such as calculating discounts, determining proportions, or measuring quantities. Mastering these topics provides the foundation for more complex calculations and helps students develop a clear understanding of numerical relationships.
Expressions and Equations
Another critical area involves understanding and working with basic expressions and simple equations. Students learn to manipulate variables and solve for unknowns, which is key to mastering algebraic thinking. These concepts also play a significant role in building confidence when tackling more intricate mathematical challenges in later years.
Importance of Math Problem Solving

Developing problem-solving skills is essential for students as it not only strengthens their logical thinking but also equips them to tackle real-world challenges. The ability to break down complex problems and find solutions is fundamental not only in academics but also in everyday situations. This section highlights the significance of honing these skills and how they contribute to overall cognitive development.
Benefits of Problem Solving Skills

Problem-solving goes beyond simply finding the right answer; it cultivates a variety of important skills:
- Critical Thinking: Encourages students to analyze and evaluate different methods.
- Creativity: Helps students approach problems from new angles, often finding multiple solutions.
- Confidence: Regular practice enhances a student’s belief in their ability to solve challenges.
- Real-World Applications: Prepares students to apply problem-solving techniques in daily life.
Strategies for Effective Problem Solving
To improve problem-solving abilities, students can employ various strategies:
- Understand the Problem: Carefully read the question and identify key information.
- Plan the Approach: Break the problem into smaller, more manageable parts.
- Test Solutions: Try different methods and verify the results.
- Review and Reflect: After finding the solution, reflect on the process to reinforce learning.
How to Approach Word Problems
Word problems often pose challenges due to their combination of textual information and numerical calculations. The key to solving these types of problems is breaking them down into smaller, more manageable steps. With the right strategy, students can learn to identify what is being asked and apply the appropriate techniques to reach a solution.
Steps to Solve Word Problems

Approaching word problems systematically can help students avoid feeling overwhelmed. Here’s a simple method to follow:
- Read Carefully: Understand the context of the problem and highlight important information.
- Identify What is Asked: Determine what the question is specifically asking you to find or calculate.
- Translate to Equations: Convert the words into mathematical expressions or equations, using variables where necessary.
- Organize Information: Write down the given data and arrange it logically, which can help in visualizing the solution.
- Solve and Check: Perform the necessary calculations and review the solution to ensure accuracy.
Common Challenges and Solutions
Even with a structured approach, word problems can sometimes be tricky. Here are some common difficulties and how to overcome them:
- Misinterpreting the Question: Always re-read the problem and confirm you understand what is being asked.
- Overlooking Key Details: Pay attention to phrases such as “in total,” “per item,” or “how many more,” as they often indicate what to focus on.
- Choosing the Wrong Operation: Identify whether the problem requires addition, subtraction, multiplication, or division based on the context.
Step-by-Step Solutions for Chapter 1
This section provides detailed, step-by-step solutions to the exercises and problems found in the first chapter. By following each stage methodically, students can better understand the concepts presented and develop stronger problem-solving skills. The goal is to break down each problem into smaller, more manageable parts, ensuring a deeper understanding of the material.
Step 1: Analyzing the Problem
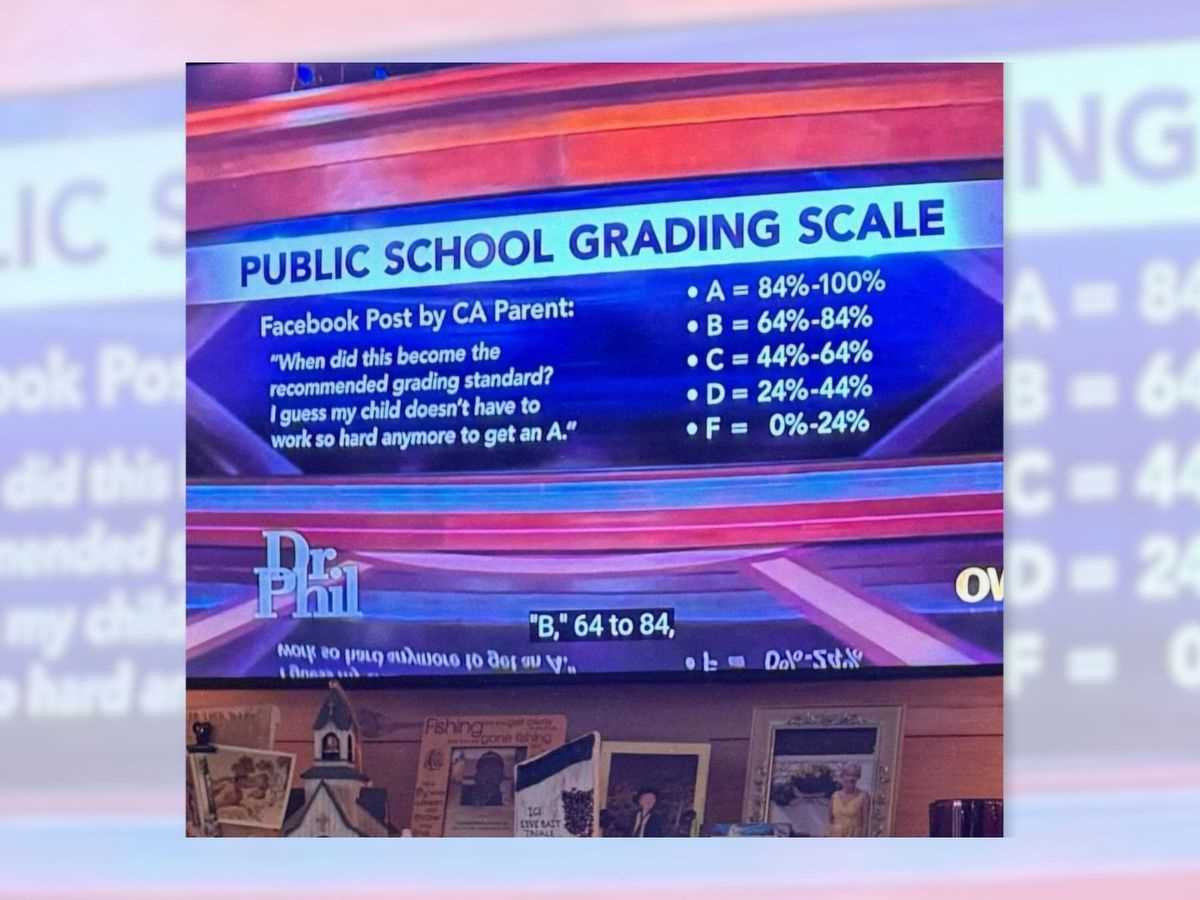
Before diving into calculations, it’s important to first analyze the problem. Here’s how to approach it:
- Read the Problem Carefully: Ensure you understand the question being asked.
- Identify Key Information: Look for important numbers, terms, and phrases.
- Determine the Goal: Know what you’re trying to solve or calculate.
Step 2: Solving the Problem

Once you’ve analyzed the problem, it’s time to apply the correct methods. Follow these steps to ensure a logical solution:
- Translate to an Equation: Convert the word problem into a mathematical expression or equation.
- Perform the Calculations: Carry out the necessary operations, step by step.
- Verify the Results: Double-check your work to ensure that your solution is correct and reasonable.
Fractions and Decimals Explained

Understanding the relationship between fractions and decimals is a key aspect of developing a solid foundation in numerical operations. Both represent parts of a whole, but they are expressed in different ways. This section will guide you through the basic concepts and help you see how these two forms of numbers can be used interchangeably.
Fractions vs. Decimals

Fractions are written as two numbers separated by a slash or line, with the top number (numerator) representing parts and the bottom number (denominator) representing the whole. Decimals, on the other hand, are written with a decimal point, showing the division of a number into ten or hundredths, thousandths, and so on.
| Fraction | Decimal |
|---|---|
| 1/2 | 0.5 |
| 3/4 | 0.75 |
| 1/5 | 0.2 |
| 2/3 | 0.666… |
Converting Between Fractions and Decimals
To convert a fraction to a decimal, simply divide the numerator by the denominator. For example, 1/2 becomes 0.5. Conversely, to convert a decimal to a fraction, express the decimal as a fraction with a denominator based on the number of decimal places. For instance, 0.75 is equal to 75/100, which simplifies to 3/4.
Exploring Ratios and Proportions
Ratios and proportions are mathematical tools used to compare quantities and express relationships between them. These concepts play an important role in many real-world applications, from cooking recipes to financial calculations. By understanding how to work with ratios and proportions, students can solve problems that involve scaling, rates, and comparisons.
Understanding Ratios
A ratio expresses the relationship between two numbers. It can be written in different forms, such as “a to b” or as a fraction. Ratios are commonly used to compare the sizes of two quantities and can help simplify complex problems by providing a clear relationship.
| Ratio | Equivalent Forms |
|---|---|
| 3 to 4 | 3:4, 3/4 |
| 5 to 2 | 5:2, 5/2 |
| 7 to 8 | 7:8, 7/8 |
Understanding Proportions
A proportion is an equation that shows two ratios are equal. For example, if the ratio of apples to oranges is 2:3, a proportion can help determine how many apples there are if the number of oranges is known. Solving proportions often involves cross-multiplying and simplifying to find the unknown quantity.
Mastering Expressions and Equations
Understanding how to manipulate expressions and solve equations is a fundamental skill in algebra. These tools help to represent relationships between quantities and are used to solve a variety of real-world problems. By mastering the art of simplifying expressions and solving equations, students can approach more complex mathematical challenges with confidence.
Understanding Expressions
An expression is a combination of numbers, variables, and operations. Unlike equations, expressions do not have an equal sign. The goal when working with expressions is often to simplify them as much as possible, making them easier to work with in later steps.
Example: In the expression 3x + 5, 3 is multiplied by the variable x>, and then 5 is added. Simplifying or evaluating expressions involves replacing the variable with a specific number.
Solving Equations
Equations, on the other hand, contain an equal sign and show that two expressions are equal to one another. Solving an equation involves finding the value of the variable that makes the equation true. This often requires isolating the variable on one side of the equation.
Example: To solve the equation 2x + 3 = 11, subtract 3 from both sides to get 2x = 8, and then divide by 2 to find x = 4.
Interactive Tools for Better Learning
In today’s digital age, interactive tools play a crucial role in enhancing learning experiences. These resources offer students a hands-on approach to understanding complex concepts, allowing them to engage with the material in a more meaningful way. By using interactive tools, learners can visualize problems, practice skills, and receive immediate feedback, making learning both effective and enjoyable.
Benefits of Interactive Learning Tools
Interactive tools provide several advantages over traditional learning methods, such as:
- Instant Feedback: Students receive real-time responses, helping them identify and correct mistakes quickly.
- Engagement: Interactive activities are often more engaging, keeping students motivated and focused on the task.
- Personalized Learning: These tools can adapt to individual learning speeds and needs, offering customized support.
- Improved Retention: Active participation enhances memory retention, leading to a better understanding of the material.
Examples of Interactive Tools
Below are some popular tools that help students strengthen their understanding of concepts:
| Tool | Description |
|---|---|
| Online Simulations | Virtual environments where students can experiment with concepts and see immediate results. |
| Interactive Quizzes | Self-assessment tools that allow students to practice skills and receive instant feedback on their answers. |
| Virtual Whiteboards | Tools that allow students to solve problems and collaborate in real-time with instructors or peers. |
Common Challenges in Grade 6 Math
As students progress in their learning, they often encounter new challenges that require more advanced problem-solving skills. In particular, certain topics tend to be more difficult due to their complexity or the need for a deeper understanding of underlying concepts. By identifying these common hurdles early on, students and educators can focus on strategies to overcome them and strengthen mathematical abilities.
Understanding Fractions and Decimals
One of the most frequent challenges in this level of education is mastering the relationship between fractions and decimals. Converting between these two forms, as well as performing operations like addition, subtraction, multiplication, and division, can be difficult without a strong grasp of the fundamental concepts. It often requires practice and a clear understanding of how fractions and decimals interact.
Working with Ratios and Proportions
Another challenge students face is understanding ratios and proportions. While these concepts are crucial for solving many real-life problems, students sometimes struggle to see how the two quantities relate to one another. This can lead to confusion when solving problems that involve scaling, rates, or comparing quantities in different situations.
Tips for Improved Math Performance
Achieving success in solving mathematical problems requires consistent effort, understanding of key concepts, and the ability to apply different strategies. By adopting effective study habits, students can enhance their problem-solving skills and approach challenges with greater confidence. Below are several tips designed to improve overall performance and understanding.
Effective Study Habits
One of the most important aspects of excelling in any subject is developing the right study routine. Consistency and focus are essential for mastering concepts. Here are some practical habits to consider:
| Tip | Description |
|---|---|
| Practice Regularly | Daily practice helps reinforce concepts and improves problem-solving speed. |
| Break Down Problems | Instead of trying to solve everything at once, break complex problems into smaller, manageable steps. |
| Seek Help When Needed | Don’t hesitate to ask teachers, classmates, or use online resources when concepts are unclear. |
| Review Mistakes | Carefully go over errors made in practice problems to understand where things went wrong. |
Utilizing Tools and Resources
Another way to improve is by taking advantage of various tools and resources that aid in learning. These can offer personalized practice and make complex problems easier to understand. Some options include online platforms, educational apps, and interactive games that engage students while reinforcing concepts.
Real-Life Applications of Math Skills
Understanding how to solve mathematical problems is not only essential in the classroom but also has numerous practical applications in everyday life. By mastering core concepts, students develop critical thinking and problem-solving skills that extend far beyond their academic studies. These skills are used in various fields, helping individuals navigate and solve real-world challenges effectively.
From managing personal finances to understanding data trends, the ability to apply mathematical principles is vital for making informed decisions. Whether it’s calculating expenses, cooking recipes, or even understanding the measurements involved in building a project, mathematical knowledge plays a key role in achieving accuracy and efficiency in daily tasks.
Budgeting and Financial Planning
One of the most direct ways math is applied in real life is in managing finances. Creating a budget, calculating savings, and planning for future expenses all require a solid understanding of numbers and calculations. By learning how to handle percentages, add and subtract figures, and work with ratios, individuals can make better financial decisions and track their progress toward financial goals.
Design and Architecture
In fields like construction and design, math is indispensable. Professionals in these areas regularly use geometry, measurements, and proportions to create accurate plans and blueprints. Whether designing a home, planning a garden, or even setting up a room’s layout, an understanding of dimensions and space is essential for ensuring everything fits together as planned.
In addition, technology and engineering fields heavily rely on mathematical principles to create everything from machines to software applications. These industries depend on the precise application of formulas and algorithms to ensure functionality and efficiency in their products and systems.
Using Practice Tests Effectively
Practice tests are a valuable tool in mastering new concepts and reinforcing knowledge. When used correctly, they help identify strengths and weaknesses, allowing learners to focus their efforts where improvement is needed. Rather than simply being a way to assess progress, practice exams serve as an opportunity to refine skills and boost confidence before actual assessments.
By incorporating regular practice tests into a study routine, students can enhance their retention and develop a deeper understanding of the material. Additionally, these tests help improve time management and familiarize learners with the test format, which can reduce anxiety during the actual exam.
Strategies for Effective Use of Practice Tests
- Take Tests Under Timed Conditions: Simulating real exam conditions helps build time management skills and reduces stress during the actual test.
- Review Mistakes Thoroughly: After completing a practice test, take the time to go through incorrect answers and understand why mistakes were made. This can highlight areas that need further focus.
- Break Tests into Sections: Rather than taking an entire test at once, split it into smaller sections to focus on specific areas and gradually improve your performance.
- Take Multiple Practice Tests: Repetition is key in reinforcing knowledge. Regular practice helps solidify concepts and improve overall performance.
Maximizing the Benefit of Practice Tests
- Track Progress: Keep track of scores and areas of improvement over time to see how you’re advancing and where more work is needed.
- Simulate Real Exam Scenarios: Use practice tests to simulate the real exam day environment, including taking breaks as needed and following the same rules that will apply in the actual assessment.
- Set Specific Goals: Before taking a practice test, set goals for what you want to achieve, such as mastering a specific concept or achieving a certain score.
By implementing these strategies, practice tests become not just a tool for assessment, but a method for enhancing learning and preparing for success in any subject.
How to Review Math Concepts
Reviewing key concepts effectively is essential for reinforcing understanding and ensuring long-term retention. A structured approach to revisiting previously learned material helps to solidify knowledge and increase confidence in applying concepts to new problems. The goal is not only to remember the steps involved but also to understand the underlying principles.
When reviewing topics, it’s important to focus on active engagement with the material rather than passive reading. This means practicing problems, seeking alternative explanations, and testing one’s understanding through various methods.
Effective Strategies for Reviewing Concepts
- Start with a Recap: Begin by reviewing notes, textbooks, or online resources to refresh your memory of key ideas.
- Practice Regularly: Consistent practice with problems helps reinforce learned material and improve problem-solving skills.
- Use Visual Aids: Diagrams, charts, and other visual tools can help clarify complex concepts and make them easier to remember.
- Teach Someone Else: Explaining concepts to others is a powerful way to test your understanding and reinforce your knowledge.
- Break It Down: Focus on one concept at a time, breaking it into smaller, manageable pieces for better clarity and understanding.
Additional Tips for Efficient Review
- Use Practice Tests: Taking quizzes or mock tests allows you to assess your understanding and identify areas that need more attention.
- Work with Study Groups: Collaborating with peers provides different perspectives and can make reviewing more engaging and effective.
- Set Review Goals: Establish clear, achievable goals for each review session to stay focused and track progress.
- Stay Consistent: Regular, short review sessions are more effective than cramming large amounts of information at once.
By employing these strategies, reviewing core concepts can be an active, rewarding experience that enhances both comprehension and application skills in problem-solving situations.
Collaborative Learning for Success
Collaborative learning is a powerful approach to mastering challenging subjects, particularly when complex concepts need to be broken down and understood from different angles. Working together with peers allows students to share ideas, explore solutions, and support each other through difficult problems. This collaborative approach encourages active engagement and fosters deeper understanding through shared knowledge and discussion.
When students collaborate, they can discuss various strategies for solving problems, clarify doubts, and learn different perspectives on the same topic. This process often leads to stronger problem-solving skills and the ability to apply learned concepts in varied contexts. The social aspect of learning in groups also builds confidence, making students more comfortable with the material.
Group study is particularly effective because it not only offers emotional support but also helps in the practical application of concepts through group exercises, discussions, and joint problem-solving. By sharing knowledge, everyone benefits from the collective wisdom of the group.
Resources for Extra Help in Learning
When faced with difficult topics or challenging exercises, additional resources can make a significant difference in a student’s ability to understand and apply key concepts. Whether it’s through online platforms, tutoring services, or collaborative study groups, there are many ways to get the extra help needed for academic success. Utilizing these resources effectively can provide clarity and improve performance in tackling complex problems.
Online Platforms and Websites

Various educational websites and platforms provide interactive lessons, exercises, and step-by-step guides that cater to different learning styles. These tools often allow students to work at their own pace and revisit tricky concepts as needed. Some notable platforms include:
- Khan Academy: Offers free instructional videos and practice exercises across a range of topics.
- IXL: Provides comprehensive practice problems with immediate feedback.
- Coursera: Offers courses designed by universities that cover a wide range of academic subjects.
In-Person and Online Tutoring
Another effective way to seek extra help is through tutoring, either in-person or online. Tutors can provide one-on-one sessions tailored to the student’s needs, offering personalized attention and the opportunity to ask specific questions. Many platforms offer affordable tutoring services, such as:
- Chegg Tutors: Connects students with expert tutors for live sessions.
- Wyzant: Offers personalized tutoring sessions, both online and in-person, in various subjects.
- Local Community Centers: Often provide free or low-cost tutoring for students in need.
In addition to these resources, peer study groups and school-based support services also play an essential role in helping students reinforce their knowledge and tackle any challenges they may face.