Secondary Math 2 Module 7 Answer Key

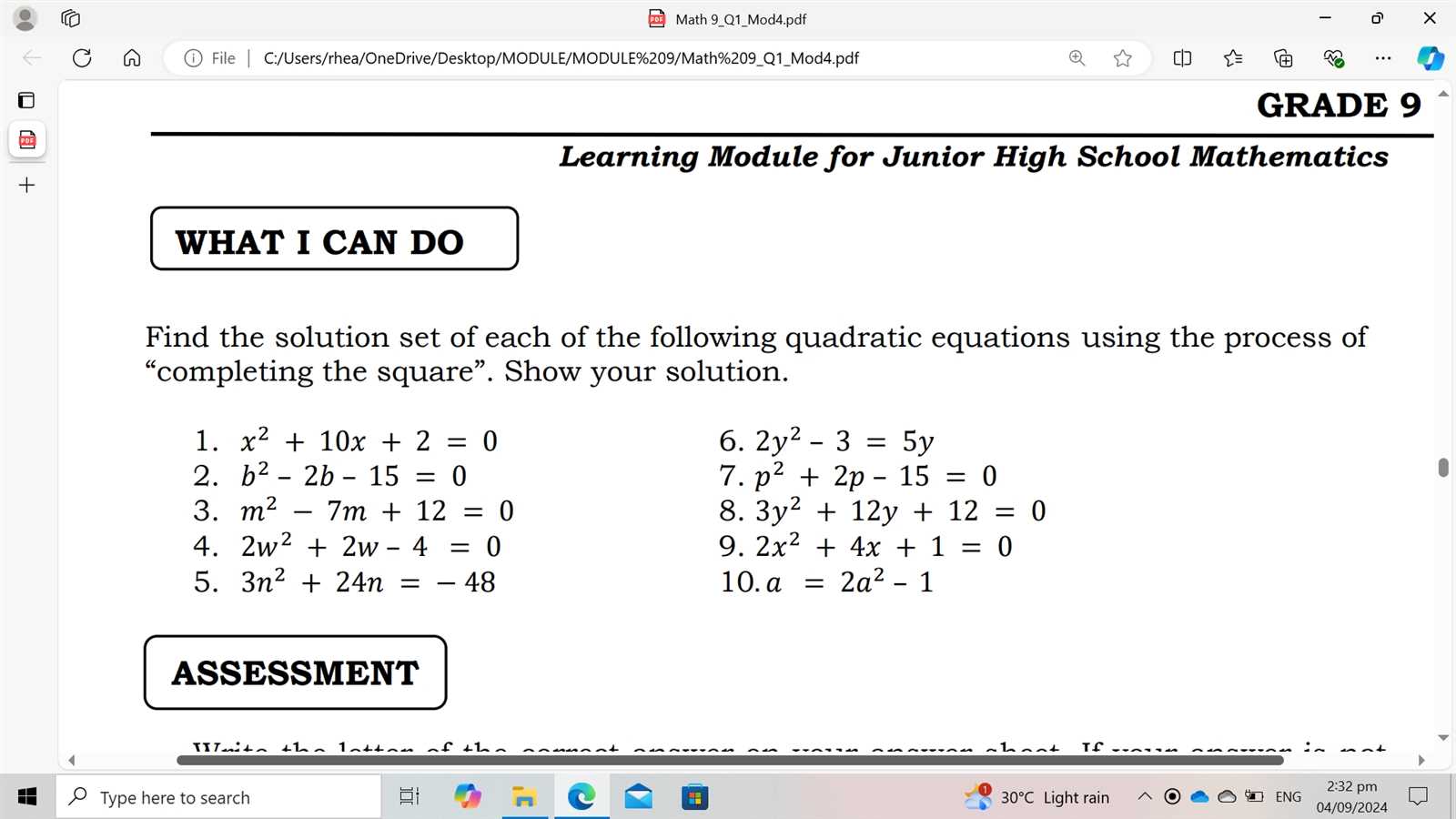
In this section, we delve into the essential solutions that will help you navigate through complex problems with confidence. With clear explanations and step-by-step guidance, we aim to simplify the concepts covered in this section and provide the tools you need for success.

Understanding key concepts is crucial when tackling challenging exercises. By breaking down each problem into manageable parts, you’ll be able to see the patterns and apply strategies that lead to accurate results. Whether you are reviewing for an exam or reinforcing your skills, this guide serves as a valuable resource for mastering the material.

Mastering these topics requires more than just memorization. With the right approach, you can build a deeper understanding that will support your learning in future subjects. As you work through the problems and review the solutions, consider how each concept connects to others to form a cohesive knowledge base.

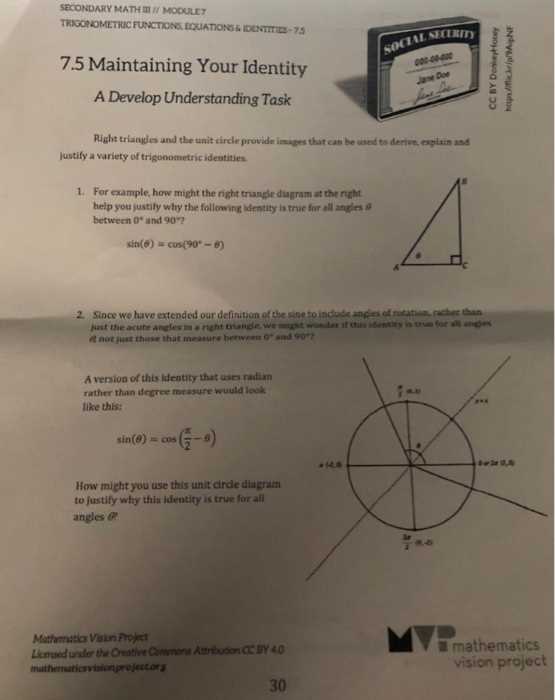
Secondary Math 2 Module 7 Answer Key

This section provides a comprehensive breakdown of the solutions to the problems found in the seventh part of the course. By exploring the steps involved in solving each exercise, learners can better understand how to approach similar tasks in the future. The following tables offer detailed explanations that clarify the reasoning behind each solution.

Understanding the Problem-Solving Process

Breaking down problems into smaller, manageable steps is key to achieving accurate results. Each task can be understood as a series of logical steps that lead to the solution. By following a structured approach, the process becomes much easier to navigate and apply in different contexts.

Key Steps for Solving the Exercises

The following table outlines the important steps involved in solving the exercises from this section. It provides a clear view of the thought process and methodologies used to arrive at the correct solutions.

Problem	Step 1	Step 2	Solution
Problem 1	Identify the given variables	Apply the appropriate formula	Result: X
Problem 2	Analyze the question	Use logical reasoning to simplify	Result: Y
Problem 3	Set up the equation	Perform the necessary calculations	Result: Z

Understanding Key Concepts in Module 7

In this section, we explore the foundational ideas that form the basis of the exercises and tasks presented. A clear understanding of these core principles is essential for successfully navigating and solving the problems. By grasping these concepts, learners can more easily apply them to a wide variety of challenges and develop a deeper comprehension of the material.

Here are the fundamental concepts to focus on for mastering this part of the course:

• Problem Decomposition: Breaking down complex problems into smaller, simpler parts is critical. This helps in identifying the correct approach and ensuring all aspects of the problem are addressed.
• Logical Reasoning: Using logical steps to connect information and solve problems methodically is a key skill in achieving accurate results.
• Formula Application: Understanding which formulas to apply in different scenarios is essential. Knowing when and how to use each formula leads to more efficient problem-solving.
• Patterns and Relationships: Recognizing patterns within the data or equations can simplify problem-solving and reveal underlying structures.

By mastering these concepts, learners will be able to approach each task with greater confidence and accuracy. The next step is to apply these principles in practice, reinforcing the knowledge through problem-solving exercises and further study.

Steps to Solve Module 7 Problems

To successfully tackle the challenges in this section, it’s essential to follow a structured approach. Breaking down each problem into clear, actionable steps will not only make the process easier but also ensure accuracy in your solutions. By following these steps, you can develop a logical and systematic method for solving any problem in this section.

Here are the key steps to follow:

• Read the Problem Carefully: Begin by thoroughly reading the question to ensure you understand what is being asked. Identify the given information and the goal.
• Identify Relevant Concepts: Recognize which principles or formulas apply to the problem. This is critical for selecting the right approach.
• Organize Information: Lay out the given data in an organized manner. This will help you see any patterns or relationships that may simplify your work.
• Execute Calculations: Apply the appropriate methods and perform the necessary calculations step by step, ensuring accuracy at each stage.
• Double-Check Results: After reaching a solution, review your work to confirm the results are correct. Look for any mistakes or miscalculations.

By following these steps, you can efficiently solve the problems in this section and build a strong foundation for tackling future challenges. Practice is key to mastering these techniques and improving your problem-solving skills over time.

Common Mistakes in Math Module 7

When solving problems in this section, there are several common errors that many learners encounter. Recognizing and avoiding these mistakes can significantly improve both accuracy and efficiency. By understanding the most frequent pitfalls, you can ensure that your approach remains focused and that your solutions are reliable.

Overlooking Key Details

One of the most frequent mistakes is overlooking important details within the problem statement. Whether it’s missing a sign, misunderstanding a variable, or not recognizing specific instructions, such errors can lead to incorrect results. Always make sure to read the problem carefully and highlight key pieces of information.

Incorrect Formula Application

Another common issue is applying the wrong formula or using it incorrectly. Different types of problems require different approaches, and using a formula that doesn’t suit the situation can easily lead to mistakes. Make sure you identify the correct formula for each type of task and apply it step by step.

Being aware of these common mistakes is crucial to improving your problem-solving skills. With practice and attention to detail, you can avoid these errors and build greater confidence in your ability to solve complex problems accurately.

How to Improve Problem-Solving Skills

Enhancing your ability to solve problems effectively requires practice and the development of certain strategies. By refining your approach, you can tackle challenges more efficiently and build a stronger foundation for future tasks. Focusing on key techniques will enable you to think critically and systematically, leading to better results.

Here are some strategies to improve your problem-solving abilities:

• Break Problems into Smaller Parts: Dividing complex tasks into simpler, more manageable components helps in understanding the problem better and addressing each part individually.
• Understand the Fundamentals: Make sure you have a solid grasp of the basic concepts that underpin the problem. Strengthening your foundation ensures that you can approach new problems with confidence.
• Practice Regularly: Regular practice allows you to apply different techniques and become more familiar with various problem types. The more you practice, the faster and more accurately you’ll solve problems.
• Work on Similar Problems: Solving similar problems helps reinforce your understanding of different methods and solutions. This improves your ability to recognize patterns and apply the most appropriate strategies.
• Analyze Mistakes: When you make an error, take the time to understand what went wrong. Learning from your mistakes helps you avoid repeating them and strengthens your problem-solving skills.

By consistently applying these strategies, you will gradually improve your ability to solve complex problems more efficiently and with greater confidence.

Essential Formulas for Module 7

In this section, we highlight the fundamental equations and formulas that are crucial for solving the problems presented. Mastering these formulas is essential for working through the exercises effectively and accurately. By understanding when and how to apply each one, you can streamline your approach and solve tasks more confidently.

Below are the key formulas you should be familiar with:

• Quadratic Formula: Used to solve quadratic equations of the form ax² + bx + c = 0. The solution is given by x = (-b ± √(b² – 4ac)) / 2a.
• Pythagorean Theorem: This formula is essential for finding the length of a side in a right triangle. It is expressed as a² + b² = c², where c is the hypotenuse and a, b are the other sides.
• Slope Formula: Used to find the slope of a line given two points (x₁, y₁) and (x₂, y₂). The formula is m = (y₂ – y₁) / (x₂ – x₁).
• Distance Formula: This formula calculates the distance between two points (x₁, y₁) and (x₂, y₂) on a coordinate plane: d = √((x₂ – x₁)² + (y₂ – y₁)²).
• Area of a Circle: The formula to calculate the area of a circle is A = πr², where r is the radius.

Familiarizing yourself with these essential formulas and practicing their application will allow you to approach each problem more efficiently. They serve as the backbone of many tasks in this section, and mastering them will significantly improve your problem-solving capabilities.

Tips for Acing the Math Exam

Performing well on an exam requires not only understanding the content but also employing effective strategies to approach each question. Preparation, time management, and confidence play a key role in achieving success. By following a few proven tips, you can enhance your ability to tackle any problem efficiently and score high on your exam.

Prepare with Practice

Regular practice is crucial when preparing for an exam. Working through sample problems and past tests will help you become familiar with the format and types of questions you may encounter. The more problems you solve, the more confident you’ll become in applying the concepts and formulas.

• Start Early: Give yourself enough time to review all topics thoroughly, allowing you to address weak areas before the exam.
• Use Study Aids: Make use of textbooks, online resources, and tutoring if necessary to fill in any gaps in your understanding.
• Work on Timed Tests: Simulate exam conditions by taking practice tests within the allotted time limit. This will help you manage your time effectively during the actual exam.

Stay Calm and Confident

During the exam, maintaining a calm and confident mindset is essential. Stress and anxiety can cloud your judgment and lead to errors. Take deep breaths and trust in your preparation. If you come across a difficult question, move on and come back to it later with a clearer perspective.

• Read Each Question Carefully: Before attempting to solve any problem, make sure you fully understand what is being asked.
• Work Methodically: Follow a clear, step-by-step approach to solve each problem, ensuring that you don’t skip over important details.
• Double-Check Your Work: If time permits, review your answers to catch any mistakes before submitting your exam.

By incorporating these tips into your preparation and exam strategy, you’ll be better equipped to handle the challenges and excel on your test.

Overview of Module 7 Topics

This section covers a variety of important concepts that serve as the foundation for solving complex problems. It introduces key principles and methods that are essential for approaching tasks effectively. Each topic builds on the previous one, reinforcing core skills and providing a comprehensive understanding of the material.

Here is a brief overview of the main topics covered in this section:

• Algebraic Expressions: Understanding how to manipulate and simplify expressions is a key skill. This includes working with variables, constants, and coefficients to form solutions.
• Equations and Inequalities: Solving linear and quadratic equations, as well as understanding inequalities, is essential for problem-solving. This includes both graphical and algebraic methods.
• Functions and Graphs: This topic explores how to represent relationships between variables using graphs. Understanding slope, intercepts, and the behavior of different functions is crucial.
• Probability and Statistics: Basic concepts in probability and statistics, such as calculating mean, median, mode, and interpreting data, are introduced to help in analyzing real-world scenarios.
• Geometry and Measurement: Applying geometric principles to solve problems related to angles, areas, volumes, and other spatial relationships is an important component of this section.

By mastering these topics, you will be able to approach a wide variety of problems with a more systematic and confident mindset, laying the groundwork for more advanced concepts in future lessons.

How to Use the Answer Key Effectively

Having access to a solution guide can be an invaluable resource when working through exercises, but it’s important to use it wisely. Simply looking at the correct answers isn’t enough to ensure understanding. The key to effective use lies in analyzing the steps involved in each solution, understanding the reasoning behind them, and learning how to apply these techniques to similar problems.

Here are some tips for getting the most out of your solution guide:

• Work Through Problems First: Try solving the problems on your own before consulting the solution guide. This will help you identify your strengths and areas that need improvement.
• Review Step-by-Step Solutions: When you check the answers, focus on the process rather than just the result. Pay close attention to the steps used to reach the solution and how each step is logically connected.
• Identify Mistakes: If your solution differs from the provided answer, review the steps carefully. Understanding where you made a mistake will help you learn from it and avoid repeating the same error in the future.
• Use It as a Learning Tool: Treat the solution guide as a learning resource. Don’t just look for the right answer–use it to understand why a particular method is used and how it can be applied to other problems.
• Practice Regularly: Regular practice, paired with reviewing the solution guide, ensures that you fully grasp the concepts. The more you practice, the more intuitive the problem-solving process will become.

By following these guidelines, you can turn the solution guide into a powerful tool for mastering new concepts and improving your overall problem-solving skills.

Benefits of Reviewing Module 7 Solutions

Going over solutions after completing exercises is a crucial step in the learning process. It allows you to solidify your understanding of the concepts and pinpoint areas where improvement is needed. By carefully examining each solution, you gain deeper insights into problem-solving techniques and strengthen your ability to approach similar problems in the future.

Here are some key benefits of reviewing the solutions:

• Clarifies Understanding: Revisiting the solutions helps to clarify any confusion you might have had while solving the problems. It ensures that you understand the correct methods and reasoning behind each step.
• Reinforces Key Concepts: By analyzing the solutions, you reinforce the concepts you’ve learned. Repetition and exposure to different examples help retain information more effectively.
• Identifies Common Mistakes: Reviewing solutions enables you to spot and correct mistakes in your approach, whether they’re small errors or larger conceptual misunderstandings.
• Improves Problem-Solving Skills: The more you review solutions, the more you develop a structured approach to solving problems. This boosts your ability to tackle future challenges with confidence.
• Promotes Independent Learning: Regularly checking solutions encourages independent learning. It empowers you to find mistakes and learn from them, making you more self-sufficient in your studies.

Overall, reviewing solutions is an essential part of mastering the material. It not only helps you understand what went wrong but also provides a valuable opportunity to learn and grow, ensuring greater success in future exercises and exams.

Advanced Techniques for Difficult Questions

When faced with particularly challenging problems, applying advanced problem-solving strategies can make a significant difference. These techniques often involve breaking down complex tasks into smaller, more manageable steps or using specialized methods to simplify the process. Mastering these approaches not only helps in solving difficult questions but also enhances overall problem-solving skills, preparing you for future challenges.

Below are some advanced techniques that can help you tackle the toughest problems more effectively:

Technique	Description
Working Backwards	Start with the desired outcome and work in reverse. This strategy helps you identify the steps needed to reach the solution.
Substitution Method	For systems of equations or complex expressions, substitute known values into the equation to simplify and isolate the variables.
Use of Graphs	Graphing equations or inequalities visually can provide insight into the relationship between variables and help you solve the problem more intuitively.
Divide and Conquer	Break down large, complicated problems into smaller subproblems. Solve each subproblem individually and combine the results.
Trial and Error	While time-consuming, trying different approaches or values can often lead to discovering the correct method when all else fails.

By incorporating these techniques into your problem-solving process, you can approach even the most difficult questions with confidence and clarity. Regular practice with these methods will gradually improve your ability to think critically and efficiently when faced with complex challenges.

How to Handle Word Problems in Math

Word problems can often feel overwhelming due to the amount of information presented in a narrative form. However, breaking down the problem into manageable parts and applying a systematic approach can help simplify the process. The key to success with these types of questions is to identify the relevant information, choose the right mathematical method, and carefully follow the steps needed to reach a solution.

Here are some effective strategies to help you tackle word problems with confidence:

• Read Carefully: Start by reading the problem multiple times to ensure you fully understand the situation. Pay attention to the details and underline or highlight key information such as quantities, relationships, and operations.
• Identify What is Being Asked: Determine what the problem is asking for and focus on the main objective. This will guide you in selecting the appropriate method to use.
• Organize Information: Create a list or chart of the known values, variables, and relationships in the problem. This will make it easier to spot patterns and determine which formulas or techniques to apply.
• Choose a Strategy: Decide on the best mathematical approach to solve the problem. This could involve algebraic equations, ratios, percentages, or other methods based on the problem’s context.
• Work Step by Step: Solve the problem in a series of logical steps, carefully checking each calculation as you go. Avoid rushing through the process, and make sure every step follows from the previous one.
• Double-Check the Solution: After solving, review your work to ensure the solution makes sense in the context of the problem. If possible, check your answer using an alternative method or verify it against known benchmarks.

With practice, these steps will help you approach word problems with a clear strategy and increase your problem-solving efficiency. By focusing on organization and logical reasoning, you can transform seemingly complex word problems into manageable tasks.

Understanding Graphs and Data Analysis

Graphs and data analysis are essential tools for interpreting numerical information and recognizing patterns or trends. By visually representing data, graphs provide a clear and concise way to analyze complex information, making it easier to draw conclusions and make informed decisions. Whether working with line graphs, bar charts, or pie charts, understanding how to read and interpret these visuals is crucial for solving problems in various contexts.

Types of Graphs

There are several types of graphs commonly used to display data, each serving a different purpose. Understanding their structure and the type of information they represent is essential for accurate analysis.

Graph Type	Purpose	Example Use
Line Graph	Shows trends over time or continuous data	Tracking a company’s sales growth over a year
Bar Chart	Compares discrete categories	Comparing the population of different countries
Pie Chart	Displays proportions of a whole	Breaking down the percentage of students in various majors
Scatter Plot	Shows the relationship between two variables	Analyzing the correlation between hours studied and exam scores

Analyzing Data

Once data is organized in a graph, the next step is to analyze it. This involves identifying trends, comparing values, and drawing conclusions based on the information presented. Key elements to look for during analysis include:

• Trends: Look for upward, downward, or consistent patterns in the data.
• Outliers: Identify any data points that significantly deviate from the rest, as they may indicate anomalies or errors.
• Comparisons: Compare values across categories or over time to see how they relate to each other.
• Proportions: Examine the parts of a whole, especially in pie charts or stacked bar graphs, to understand the distribution of data.

By mastering graph interpretation and data analysis, you can make more accurate decisions and understand complex data more easily. Regular practice will improve your ability to extract meaningful insights and use data effectively in various contexts.

Time Management Strategies for Module 7

Efficient time management is crucial when working through complex assignments and problems. Organizing your time helps ensure that you can tackle each concept without feeling overwhelmed. By implementing structured strategies, you can balance practice, review, and preparation, leading to a deeper understanding and improved performance.

Setting Clear Goals

Establishing specific, measurable goals is the first step in effective time management. Breaking down tasks into smaller, more manageable objectives helps maintain focus and provides a clear path forward. For example, aim to complete a certain number of problems or understand a specific concept each session.

• Prioritize tasks: Identify which sections or problems are most challenging and tackle them first.
• Time blocks: Allocate a set amount of time for each task to avoid spending too much time on one area.
• Set mini-deadlines: Create internal deadlines for completing smaller parts of the material before tackling the whole assignment.

Using Breaks Effectively

Taking breaks during study sessions can prevent burnout and improve focus. Using the Pomodoro technique, where you work for 25 minutes and take a 5-minute break, is an effective method. After several cycles, take a longer break to recharge. This method promotes sustained attention and allows you to maintain high productivity levels.

• Take strategic breaks: A short walk or a few minutes of stretching can help refresh your mind.
• Minimize distractions: Use breaks as a time to disconnect from study-related tasks completely.

By organizing your time and taking regular breaks, you will make more efficient use of each study session. These strategies will help you stay on track and avoid last-minute stress, leading to a more confident approach to tackling the material.

How to Retain Math Concepts Long-Term

Retaining mathematical principles over time requires more than just memorization. It involves understanding the underlying logic, practicing regularly, and finding ways to connect the concepts to real-world applications. This long-term retention ensures that knowledge is not only useful for exams but also applicable in future scenarios.

Practice Consistently

One of the most effective ways to cement concepts in your memory is through consistent practice. Regular exposure to problems reinforces your understanding and helps to maintain familiarity with different types of tasks. The more you practice, the better you become at recognizing patterns and applying appropriate techniques without hesitation.

• Daily practice: Set aside a small amount of time each day to solve problems, even if it’s just for a few minutes.
• Varied problems: Challenge yourself with problems that require applying different methods to solve.
• Review mistakes: Go over incorrect solutions to understand where you went wrong and solidify your learning.

Connect Concepts to Real-Life Scenarios

Understanding the practical application of mathematical concepts makes them easier to retain. Relating problems to real-life situations can help contextualize the knowledge, making it more memorable and relevant. Whether through budgeting, planning, or problem-solving, seeing the utility of what you’re learning enhances long-term retention.

• Use examples: Incorporate real-world examples, such as calculating distances or analyzing data trends, to make abstract concepts more tangible.
• Apply to everyday tasks: Look for ways to use mathematical principles in daily activities like shopping or home improvement projects.

By practicing consistently and relating concepts to real-life scenarios, you can ensure that the knowledge remains ingrained, making it easier to recall and apply in future situations.

Preparing for Future Math Modules

Successfully advancing to more complex topics in the subject requires careful preparation and a solid foundation in the current material. Strengthening your grasp on fundamental concepts now can pave the way for easier navigation through upcoming lessons. This proactive approach will help ensure that you stay ahead and are better equipped to tackle future challenges with confidence.

Master the Basics

Understanding core concepts is crucial before moving on to more advanced topics. Without a strong grasp of the basics, future content will be much harder to comprehend. Review key principles regularly and seek clarification on any points that may still be unclear.

• Focus on foundations: Prioritize mastering essential skills like algebra, geometry, and number operations that will support more advanced topics.
• Seek help early: If a concept isn’t clear, reach out for assistance rather than waiting until it becomes a larger issue.
• Utilize resources: Leverage textbooks, online tutorials, or study groups to reinforce your understanding.

Plan Ahead for Upcoming Topics

Anticipating the next series of lessons can make the transition smoother and less stressful. Familiarizing yourself with upcoming topics allows you to prepare mentally and fill in any gaps in your knowledge before you encounter them in class.

• Preview future lessons: Look ahead in your curriculum to identify the main themes or topics that will be covered.
• Research advanced concepts: Read about upcoming concepts and try to understand their relevance to what you’ve already learned.
• Work ahead: If possible, tackle a few problems or exercises from upcoming chapters to get a feel for what’s to come.

By mastering current material and preparing for the next steps, you can build confidence and reduce the pressure when new topics arise, making your learning journey smoother and more effective.